景观异质种群空间重构模型设计与仿真

王玉虎，张 楠

(1. 晋中信息学院食品与环境学院，山西 晋中 030800；2. 山西大同大学机电工程学院，山西 大同 037003)

1 引言

随着人类对自然环境的改造和破坏，景观破碎化进程逐渐加快，程度加深，恢复破碎化景观成为当前环境保护的重要方向[1，2]。景观破碎化导致种群空间隔离，进而造成原始种群分裂成局域种群，演变出相互连接的异质种群生存方式。因此，研究异质种群动态也是研究破碎化景观动态。

在研究景观空间时，张金茜使用GeoDA软件工具进行景观破碎化研究[3]，但该方法的功能较少，不能批量导入数据，效率较低。魏莉莉曾提出使用遥感技术进行景观破碎化研究[4]，遥感技术动态监测能力较差，受影响因素多。除此之外，还有学者使用一阶泰勒级数展开进行近似求解关系式，但一阶构造精确度较低。因此本文选择空间现实异质种群模型的处理方式，建立基于二阶泰勒级数展开优化的景观异质种群空间重构模型，通过该模型研究破碎化景观动态，为宏观调控破碎化景观，维持生态平衡提供科学依据。

2 景观异质种群空间重构模型

2.1 空间现实异质种群模型

空间现实异质种群模型作为异质种群模型进化的第三阶段，其具有多样空间特征，比如局域种群的空间位置和面积等，还含有破碎化景观的几何特征及其中异质种群的全部信息，拥有的信息能够直接模拟真实景观，其中关联函数模型较为典型。关联函数模型通常使用一阶线性马尔可夫模型，该模型以单个生境斑块为基础，是离散时间的随机模型[5，6]。

破碎化景观的结构为斑块化网络，斑块的性质特征决定了景观和种群动态。生境斑块存在定居和未定居两种状态，通过定居概率和灭绝概率可以确定这两种状态间的转化，并且相互独立[7]。令一个斑块为i，用Ci描述定居概率，Wi描述灭绝概率，因此有式(1)

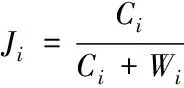
(1)

其中，Ji为单位时间斑块i被占据的静态概率，表示斑块i和物种间的关联。

Wi的数学表达式为

(2)

其中，Ai表示i的面积，当Ai≤e1/x时，i的灭绝概率为100%，这时Ai最小，等于A0；e、x为相关参数。

引入一个概念——迁入种群i的个体总数Mi，表达式见式(3)

(3)

其中，Si描述斑块i的连接度；Pi描述斑块格局，它的值取为0或1，在空白斑块取0，被占领斑块取1；dij描述斑块i到斑块j的距离；α、β、b是相关参数。由此确定定居概率的表达式

(4)

其中，y′=y/β，y为相关参数。由此式(1)可以扩展为

(5)

模型参数估计通过极大似然值θ进行，具体表达式见式(6)

(6)

当假定异质种群与随机稳定假设相近，Pi可通过极大似然函数直接用于建模，使建模效率大幅提升。模型的参数估计是关键问题。可以由非线性极大似然回归得到上文中的相关参数，此方法能够提高参数的准确性，其中，α、β、b、A0可以通过观察数据确定，但存在一定误差，因为它们和被研究物种的生物学特性相关，以上定义的特性可能会造成实际应用中的麻烦，比如定居概率的恒定性和生境斑块的独立性，以及局域种群的平衡条件和观测数据的质量等都对参数估计有一定影响，因此通过二阶泰勒级数展开完成这4项参数的优化，以应对这些可能出现的特性，提高参数估计的准确性和可操作性。

景观连接度是景观破碎化研究的重点，它不仅能反映出景观破碎化的趋势，还能反映其程度。连接度Si能够在一定条件下描述破碎化景观动态，机制和破碎化景观动态格局的关系也可以根据模型预测结果呈现在Si上。由于比格局分析法几何学角度反映的景观破碎化机制更真实，因此关联函数模型得到广泛应用。

2.2 二阶泰勒级数展开优化算法

2.2.1 二阶泰勒级数展开

为了使计算变得更加简洁，通常使用简单的函数关系近似表达一些复杂的函数关系，利用泰勒级数展开的多项式函数表达最为常见[8，9]。已知函数的某一点，这一点邻域内的函数关系可以通过一个多项式函数近似表达，而这个多项式函数由泰勒级数展开这一点的每阶导数构成。

假设函数z=z(x)在x0的邻域内连续，且有(n+1)阶导数，由泰勒中值定理有

(7)

其中，h=x-x0；ξ表示在x0到x区间内的某个值。

同理对n元函数z=z(x1，x2，…，xn)在点(x10，x20，…，xn0)某邻域内进行泰勒级数展开，得到式(8)

z(x1，x2，…，xn)=z(X0)+h1z′x1(X0)+h2z′x2(X0)

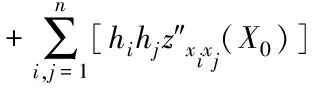
(8)

其中，X0=(x10，x20，…，xn0)；hi=xi-xi0。

隐函数不能直接进行求导，而建模参数和模型响应间恰好为这种关系，因此利用差分法求得隐函数的近似导数，解决这个难题。

扰动其中一个建模参数，使用关联函数分析软件计算出其相应的响应计算值，利用该值变化量与该建模参数的扰动量相除得到的结果为一阶偏导数，此一阶偏导数为一个近似导数，数学式见式(9)

(9)

其中，z′xi(X0)为与建模参数X0关联的模式响应函数，xi为建模参数，Δxi为xi的扰动量。

然后继续扰动xi，再得到一个一阶偏导数，该一阶偏导数的变化量和Δxi的比值则为二阶偏导数，模式响应关于xi的二阶偏导数为一个近似导数，具体数学式见式(10)

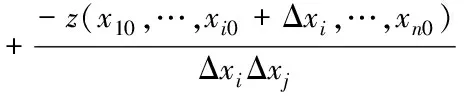
(10)

2.2.2 空间现实异质种群模型参数优化

令Uj，c为响应计算值，Ei为优化参数，它们之间的关系式为Uj，c=U1jEi，该关系式是一个近似函数，通过一阶泰勒级数展开求得。构造一个目标函数H

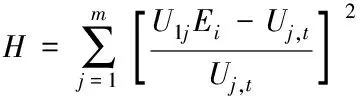
(11)

其中，Uj，t为模式响应的试验值。

向前1%扰动第i个优化参数初始值Ei0得到1.01Ei0，用fj，c和ur，c描述响应计算值，通过在优化模型中代入1.01Ei0得到fj，c(E10，…，1.01Ei0，E40)和ur，c(E10，…，1.01Ei0，E40)，在式(9)中代入1.01Ei0对应的模型响应计算值和Ei0对应的模型响应计算值fj，c(E0)和ur，c(E0)求出一阶偏导，即为频率初始计算值和位移初始计算值对优化参数的一阶泰勒级数展开。

通过一阶泰勒级数展开进行响应计算，构造目标函数，对其进行最小化处理，得到优化参数值。目标函数表达式见式(12)：

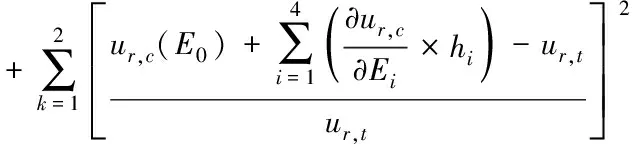
(12)

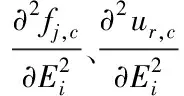
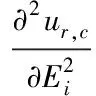
3 实验

将某地景观用作研究区域，研究二阶优化的效果和景观异质种群空间重构模型观测与预测的破碎化程度，观察人类活动对景观变化的影响，验证本文模型的应用性。

3.1 二阶优化

为了验证二阶优化的效果，对最小化目标函数得到的优化参数误差进行分析，将实验得到的误差值制成图1。

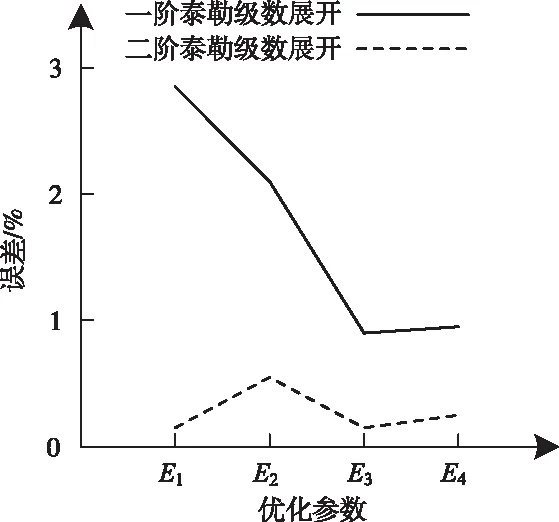
图1 泰勒级数展开优化参数误差

由图1可知，二阶泰勒级数展开优化后的参数误差与一阶相比大幅降低且更稳定，优化后最大误差为2.86%，低于3%。

将一阶和二阶泰勒级数展开优化结果制成表1，对优化后及优化前的响应计算值进行误差分析。

表1 泰勒级数展开优化响应计算值误差

由表1可知，一阶和二阶优化后的响应计算值误差和优化前相比均有大幅降低。一阶优化后的响应误差在1%左右，而二阶优化后的误差不超过0.2%。综上可知经二阶优化后的模型比一阶效果更好，更符合实际情况。由于二阶优化的计算量较大，泰勒级数展开阶数可根据实际进行调整，减少计算量。

3.2 景观破碎化分析

根据景观类型把该地景观分成六类：1.耕地；2.林地；3.草地；4.水域；5.建筑用地；6.未开发地。研究范围共18276km2。使用斑块密度指数(PD)来衡量景观破碎化程度，值越高表示破碎化程度越高。将2010年、2015年、2020年该地各类景观异质种群斑块密度指数制成图2。

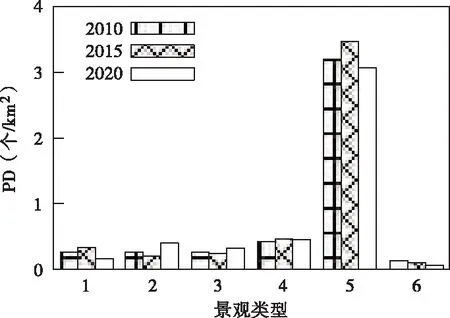
图2 景观斑块密度指数

根据图2可以看出，不同景观类型密度变化有所差异，但建筑用地密度指数始终最高。耕地斑块密度在前五年有所上升，后五年下降，而林地和草地密度在前五年下降后均有上升，这是由于随着我国退耕还林还草政策的开展与实施，增加了林地与草地的面积。但耕地分布较为集中，破碎化程度低，林地与草地由于人类活动的影响导致破碎化程度较高。

将三个时间点的景观异质种群斑块数量破碎化指数(FN)制成图3。其中FN∈(0，1)，当景观未被破坏时FN值为0，当景观被完全破坏时FN值为1。

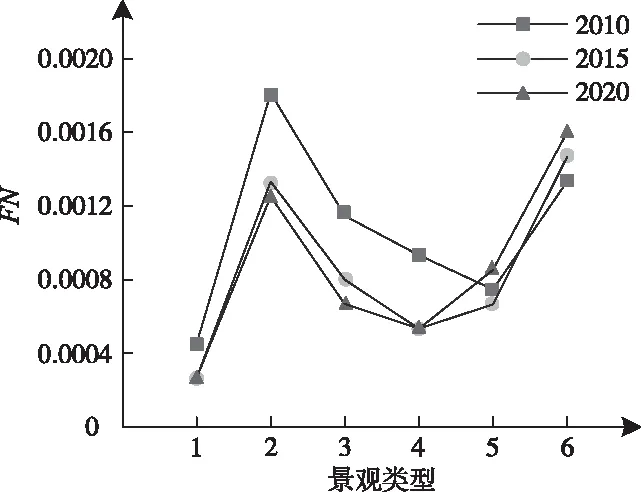
图3 景观斑块数量破碎化指数

从图3中可以看出，2010年到2015年，除了6号景观，其它景观数量破碎化指数均有所下降；该地十年间景观破碎化程度呈整体降低趋势。其中，2号景观是景观数量破碎化指数最大的景观类型，其次是6号和3号，而1号景观的数量破碎化指数最小。主要原因为人类活动对景观的影响，随着人类活动的增加，生活区域不断发展，耕地和建筑用地平均斑块面积也逐渐增大，且围绕人类生活区域分布均匀，破碎化程度逐渐降低。

将三个时间点的景观异质种群分离度指数(N)制成图4，当N值越大，斑块离散程度越大。

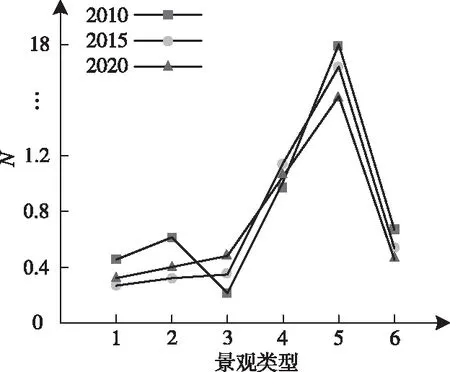
图4 景观分离度指数

从图4可看出2010年到2020年这十年间景观分离度指数的变化，建筑用地的景观分离度指数始终最高。景观分离度指数也与人类活动有密切关联，早年间建筑用地和水域景观分离度指数较高，这是由于发展初期建筑用地离散程度较大，人类活动强度较小。随着社会发展建筑用地面积显著提高，但由于其它景观类型的限制，如耕地的位置，退耕还林还草面积的上升，可开发的景观数量逐渐减少，只能在原有建筑用地基础上进行扩充，建筑用地离散程度随之降低。综上景观异质种群分离度指数随着人类活动强度增加而减小，即分离度也减小。

4 结论

本文设计的基于二阶优化的景观异质种群空间重构模型能够准确体现局部地区的景观破碎化程度，为景观建设提供有效参考。

1)通过二阶泰勒级数展开对景观异质种群空间重构模型进行优化，优化后的参数误差和响应计算值误差均有大幅降低，一阶优化后最大误差值分别为2.86%和1.62%，而二阶优化后最大误差值分别小于1%和0.2%，说明二阶泰勒级数展开的优化效果更好。

2)自然条件和人类活动共同影响景观破碎化程度，人类活动区域的发展和景观破碎化息息相关，相互制约。本文对某地景观2010年起五年为一个步长到2020年选取了景观异质种群斑块密度指数、景观异质种群斑块数量破碎化指数和景观异质种群分离度指数三个指标进行实验分析。2020年该地建筑用地景观密度指数和分离度指数均比之前降低，而景观数量破碎化指数有所上升，整体景观破碎化逐年降低。主要原因为人类活动影响其它景观类型的连续性，早期景观离散度增加，但随着生态建设意识和水平的不断提高，景观破碎化程度逐渐降低，体现出各项环保政策的正确性。