全桥LLC谐振变换器稳定性分析与仿真研究
2022-08-22岳云涛李炳华
岳云涛,王 成,李炳华
(1. 北京建筑大学电气与信息工程学院,北京 100044;2. CCDI悉地国际集团,北京 100013)
1 引言
近年来LLC谐振变换器被广泛应用于电动汽车充电设备、航空二次电源、UPS和固态变压器、光伏系统直流变换器等领域中,实现电压变换及能量传输等重要功能。如果LLC谐振变换器稳定性存在缺陷,会导致扰动情况下变换器的输出不能满足预期性能指标,对系统造成伤害甚至崩溃[1]。为提高LLC谐振变换器的输出性能,增强系统的抗干扰能力,在设计过程中对变换器进行整体稳定性分析尤为重要。
对LLC谐振变换器的建模是对其进行稳定性分析的关键,通常LLC谐振变换器采用变频控制,此时谐振网络利用基波进行能量传输,开关频率近似等于谐振频率,这就导致状态平均建模法不再适用[2]。而LLC谐振变换器的非线性很强,且存在多个工作状态,利用传统稳定性分析方法在传递函数构造过程存在困难[3-5]。文献[6]针对LLC谐振变换器采用扩展函数描述法构建模型,得到电路等效模型和传递函数,并设计了控制环路反馈补偿器最后利用Bode图验证稳定性。文献[7-10]则分别对LLC谐振变换器、LC谐振变换器、LCC谐振变换器进行了数学模型构造与稳定性分析,但过程中存在大量高阶传递函数的计算,分析过程复杂。文献[11]则针对半桥LLC谐振变换器进行不同电路参数下的频率特性曲线动态分析,对整体稳定性评价欠缺。文献[12]基于时域给出了变换器每个工作状态下的时域方程,但并未得出统一的方程组。文献[13]将基波分析法与时域分析法相结合对模型中谐振因数重新定义,但缺乏理论依据,无法判断其正确性。在实际应用中,控制回路参数的变化往往会因其整体电路工作状态及输出性能的变化,但以上建模过程针对变换器本身进行频域开环分析,常体现在电路特性分析及参数设计,并未将闭环控制过程考虑进稳定性分析过程中,闭环稳定性物理概念不够清晰。
本文针对全桥LLC谐振变换器及其控制回路,首先基于扩展描述函数法构建系统整体状态方程;其次结合Floquet理论对系统状态传递矩阵进行推导,并将此矩阵作为稳定性分析基本依据;接着利用Floquet稳定性判据判断全桥LLC谐振变换器整体稳定性,确定闭环控制参数稳定范围。最后通过仿真与传统开环分析结果对比证明方法正确性并进一步确定控制参数稳定范围。整个过程完全基于时域分析,避免了传统方法中对高阶传递函数的求解过程,有利于在一定程度上降低LLC谐振变换器稳定性分析复杂程度。
2 全桥LLC谐振变换器闭环建模
2.1 全桥LLC谐振变换器工作原理
全桥LLC谐振变换器的典型拓扑如图1所示,主要由全桥逆变电路、谐振腔、变压器和整流滤波电路组成[14]。全桥LLC谐振变换器的工作频率与电压增益关系如图2所示,全桥LLC谐振变换器工作时大致可分为三个区域:区域1属于容性工作区域,此时系统损耗大且转换效率低,无法实现零电压导通,不利于变压器设计,一般不工作于此区域内[15];区域2与区域3均为感性工作区域,系统均实现零电压导通,区别在于区域2电压增益大于1,此时系统几乎不受死区时间影响;而区域3电压增益小于1,此时死区时间对LLC转换效率、零电压导通及稳定性均存在一定影响。因而在模型建立的过程中需视情况区分对待,这也导致了全桥LLC谐振变换器在不同工作模式下存在不同的数学模型,其系统传递函数难以得到。另外,仅考虑开环下的数学模型而忽略闭环控制器对变换器工作过程稳定性的影响,同样也是以往LLC谐振变换器稳定性分析的一大缺陷。
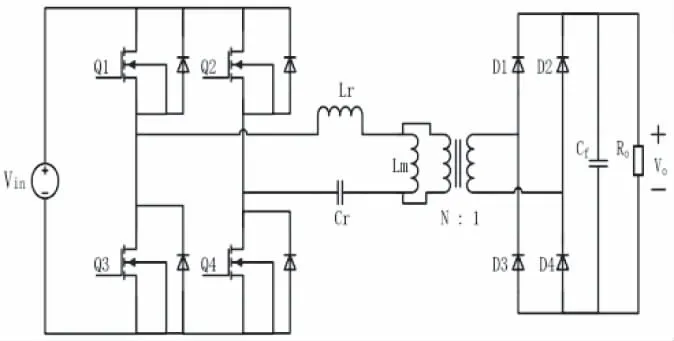
图1 全桥LLC谐振变换器拓扑

图2 全桥LLC谐振变换器频率-增益曲线
2.2 闭环系统状态方程组
2.2.1 闭环反馈方式条件
区别于以往研究中仅考虑变换器本身的等效电路的情况,本文研究中将控制回路及闭环反馈部分均考虑入建模过程中。控制回路如图3所示。
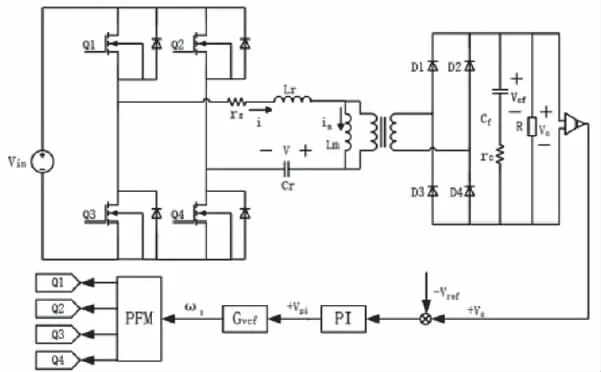
图3 全桥LLC谐振变换器等效电路拓扑
研究中根据采样时刻输出电压与参考电压的偏差值作为PI控制器的输入,经闭环PI计算后,通过压控振荡器将所得电压偏差值VPI转换为其所对应的系统开关频率,最后经由PFM控制器生成幅值相同互补的两路脉冲信号对变换器内部功率管进行开关切换控制并实现输出稳压。此种控制方法简化了控制回路设计,是输出响应得到快速稳定,同时令全桥LLC谐振变换器电路直流输出更加稳定[16]。
图3中ωs表示的是系统开关角频率,表示为
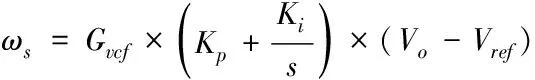
(1)
其中,Gvcf为压控振荡器等效比例系数,Kp与Ki分别为PI控制器的比例系数及积分系数;Vo为系统输出电压;Vref为系统控制回路参考电压。
2.2.2 全桥LLC谐振变换器整体建模
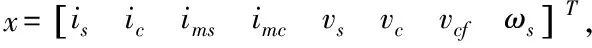
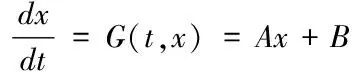
(2)

其中,ips、ipc为变压器原边电流正余弦分量;ipp为变压器原边电流幅值,具体大小为

式中除各状态变量定义外,Lr为谐振电感值;Lm为励磁电感;Cr为谐振电容;Cf为输出滤波电容;R为输出负载电阻值;rc为输出滤波电容寄生电阻;rs为谐振网络寄生电阻;n为变压器变比。
3 基于Floquet理论的全桥LLC谐振变换器稳定性分析
3.1 Floquet稳定性判据
Floquet理论是立足于经典稳定性理论思想得到的针对周期系数线性微分方程解的稳定性理论,故Floquet理论有很强的研究周期系统稳定性适用性[19-21],近几年已成功应用于直流式分布电源系统、级联DC-DC变换器、光伏逆变器及部分交流系统等典型周期系统的稳定性分析。Floquet理论一般利用系统的状态传递矩阵的最大特征值状态判断周期运动稳定性[22]。针对全桥LLC谐振变换器存在不同工作状态下状态方程的问题,可将变换器视为一个周期任意的周期系统,故根据Floquet理论可知,此时对系统状态方程组对应摄动方程组零解稳定性进行研究即可判断系统稳定性。
将摄动方程基本解矩阵假设为ψ(t),则必存在
φ(t)=A(t)etD
(3)
对于周期系统则必存在
φ(t+T)=φ(t)C
(4)
其中C是一个可逆矩阵[23]。对于一个稳定的LLC谐振变换器系统,其摄动方程基本解矩阵只存在一个,则
φ(t+T)=A(t+T)et+TD=φ(t)etD
(5)
可知
C=etD
(6)
假设此时系统中不含周期交流扰动,故式(6)中T为系统周期,D为摄动方程在稳态解处对应的雅可比矩阵。将系统状态传递矩阵定义为矩阵C,则将矩阵C的特征值定义为Floquet乘子。Floquet稳定性判据仅与Floquet乘子模的最大值有关[23],具体判据如下:当Floquet乘子模的最大值小于或等于1时,认为全桥LLC谐振变换器是稳定或临界稳定的;当Floquet乘子模的最大值大于1时,认为全桥LLC谐振变换器是不稳定的。
3.2 Floquet乘子推导

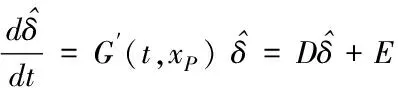
(7)
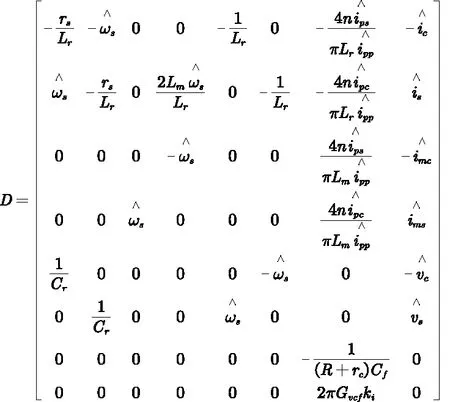
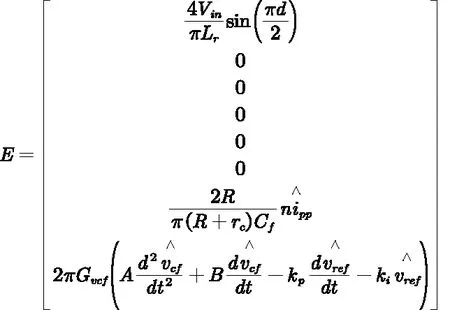
式(7)中各状态变量定义与式(2)保持一致,上标表示摄动量以与式(2)区分。其中部分变量表示为:
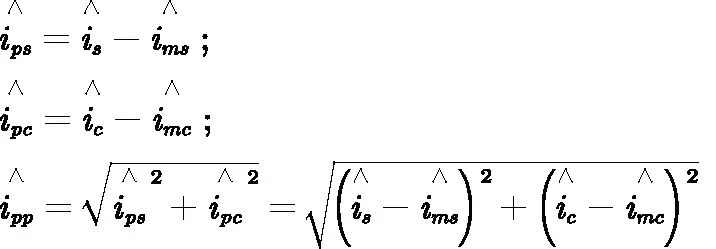
将系统雅各比矩阵设为JF(t,xP),那么

(8)

其中:
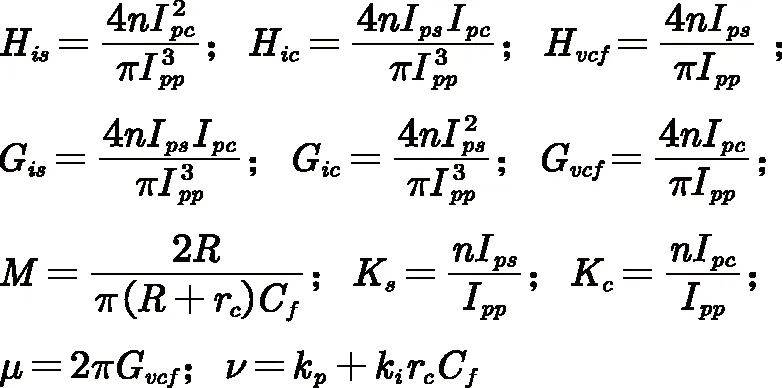
由于系统稳态周期解因各状态变量的高频开关纹波被滤除为常量,故包含稳态周期解的雅各比矩阵也可视为常数矩阵。故系统状态传递矩阵为:
C=etJF
(9)
根据Floquet理论,将系统状态传递矩阵C特征值作为Floquet乘子对全桥LLC谐振变换器进行稳定性分析。
3.3 理论结果分析
本文中采用的具体电路参数如下:Vin=400V;Lr=40μH;Lm=450μH;Cr=282nF;n=8;Cf=1000μF;rs=5mΩ;rc=5mΩ;R=16.667Ω;D=0.5;Gvcf=100000。首先设kp=0.006;ki=60使系统超调量较小以获得较好的动态特性。将以上参数结合式(9)与Matlab中进行特征值求解并与单位圆作比较,结果如下。
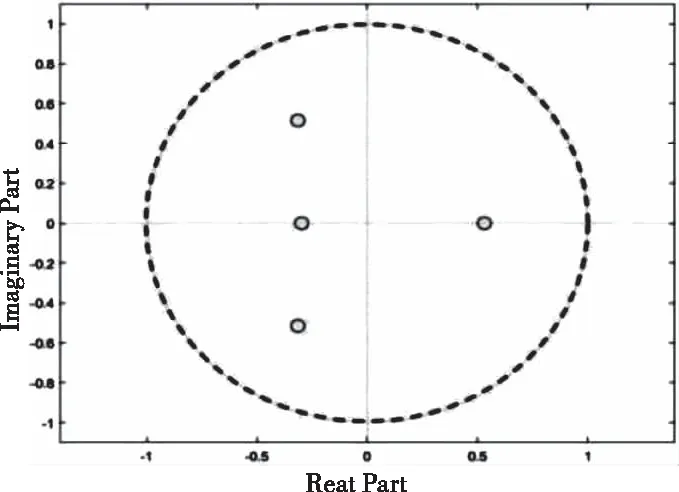
图4 kp=0.006、ki=0.13时矩阵C特征值分布情况
由计算结果可以看出在此参数条件下,矩阵C的所有特征值在复平面内均位于单位圆之内,即最大特征值的模小于1,系统处于稳定状态。另外,通过式(9)及计算结果可知,特征值求取与控制器控制系数有关,控制系数改变,其特征值也随之改变进而影响系统稳定性。接下来在其它电路参数不变的情况下,通过改变控制器的控制系数来具体分析全桥LLC谐振变换器的稳定性。
3.3.1 固定比例控制系数kp=0.006不变,改变积分控制系数ki
ki从30到90变化时特征值轨迹如图5所示。固定比例系数Kp=0.006,当积分控制系数Ki<80时,系统状态传递矩阵的特征值均位于单位圆内,即特征值模长均小于1,此时系统处于稳定状态;当积分系数Ki=80左右时,系统状态传递矩阵的特征值有部分位于单位圆上,此时系统处于临界稳定状态;当Ki=80时,已有特征值位于单位圆之外,故可合理推测当Ki>80,系统不稳定。综上可知,此组电路参数下控制系数理论稳定范围为Kp=0.006,Ki≤80。

图5 ki从30到90变化时特征值轨迹(A.整体图B.局部图)
3.3.2 固定积分控制系数ki=60不变,改变比例控制系数kp
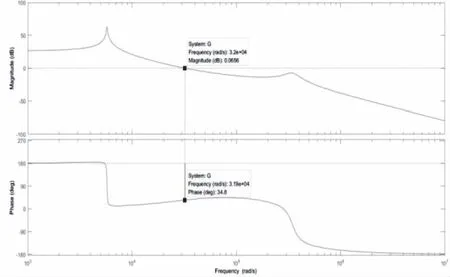
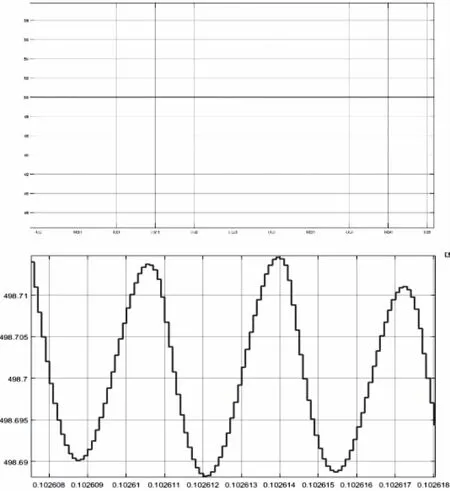
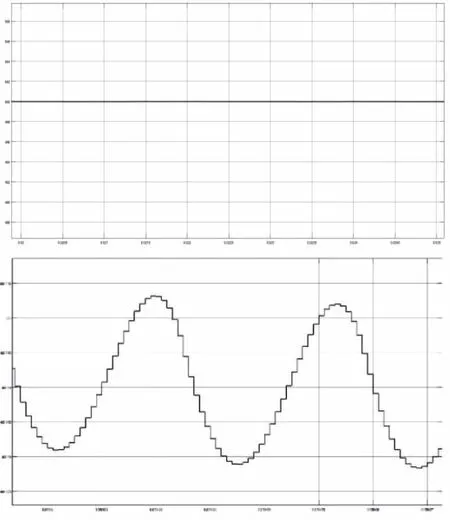
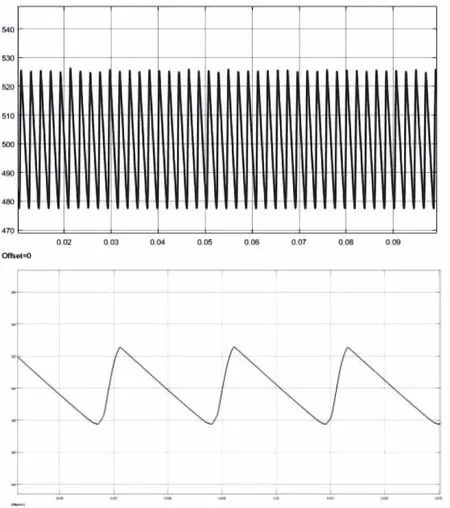
kp从0.01到0.12变化时特征值轨迹如图6所示。固定积分系数ki=60,当比例控制系数Kp<0.01时,系统状态传递矩阵特征值均位于单位圆内,即特征值模长均小于1,此时系统处于稳定状态;当积分系数Kp=0.01左右时,系统状态传递矩阵的特征值有部分位于单位圆上,此时系统处于临界稳定状态;当Kp>0.01时,已有特征值位于单位圆之外,故可合理推测当Kp>0.01,系统不稳定。综上可知,此组电路参数下控制系数理论稳定范围为Ki=60,0.001 图6 kp从0.01到0.12变化时特征值轨迹(A.整体图B.局部图) Bode图绘制简单,可准确提供稳定性和稳定裕度信息,而且还能大致衡量闭环稳态和动态性能,多被用来分析LLC谐振变换器闭环稳定。为验证Floquet理论稳定性分析的正确性,利用Bode图结合上述电路参数对全桥LLC谐振变换器进行开环频域特性分析。 全桥LLC谐振变换器开环Bode图如图7所示。由于开关角频率与输出电压变化方向相反,故相频曲线始于180°线且在高频段开环幅频特性衰减很大,此时幅值稳定裕量为-26.6dB,相角稳定裕量为34.8°,幅值穿越频率为3.19×104rad/s。由各稳定裕量分析可知在参考电路参数下,全桥LLC谐振变换器闭环系统稳定,与Floquet稳定性分析方法结果相同,证明本文稳定性分析方法的准确性。 图7 全桥LLC谐振变换器开环Bode图 全桥LLC谐振变换器开环Bode图如图7所示。由于开关角频率与输出电压变化方向相反,故相频曲线始于180°线且在高频段开环幅频特性衰减很大,此时幅值稳定裕量为-26.6dB,相角稳定裕量为34.8°,幅值穿越频率为3.19×104rad/s。由各稳定裕量分析可知在参考电路参数下,全桥LLC谐振变换器闭环系统稳定,与Floquet稳定性分析方法结果相同,证明本文稳定性分析方法的准确性。 为确认理论稳定性范围的准确性,在Matlab/Simulink中建立全桥LLC谐振变换器闭环PI控制模型进行仿真,其中,仿真时谐振频率设置为50kHz,工作频率接近谐振频率,工作于感性负载区域。通过变化控制器的控制参数观察LLC谐振变换器输出电压波形变化,对其输出稳定性及系统稳定性进行分析。 当Ki=60,Kp=0.010时,结果如图8所示。系统基本无震荡,电路工作过程平稳快速,整体输出电压平衡在500V,上下波动不超过0.2V,输出电压波形稳定为正弦波,从而可以看出全桥LLC谐振变换器在此时属于稳定状态;当Ki=60,Kp=0.011时,结果如图9所示。输出电压在仿真时间内未达到稳定,输出电压持续上升,同时输出波形不能很好地保持正弦波姿态,输出电压发生震荡,此时全桥LLC谐振变换器属于不稳定状态。仿真稳定范围为Ki=60,0.001 图8 Ki=60,Kp=0.010的全桥LLC谐振变换器输出电压波形(A.整体图B.放大图) 图9 Ki=60,Kp=0.011的全桥LLC谐振变换器输出电压波形(A.整体图B.放大图) 当Ki=80,Kp=0.006时,结果如图10所示。系统基本无震荡,整体输出电压基本保持500V,输出电压波形呈现为正弦波,可以看出全桥LLC谐振变换器状态稳定;当Ki=90,Kp=0.006时,结果如图11所示。输出电压震荡剧烈,输出电压在478-525V之间波动,因此可判定此时全桥LLC谐振变换器不稳定。仿真稳定范围为Kp=0.006,Ki≤80,与理论分析结果一致。 图10 Ki=80,Kp=0.006的全桥LLC谐振变换器输出电压波形(A.整体图B.放大图) 图11 Ki=90,Kp=0.006的全桥LLC谐振变换器输出电压波形(A.整体图B.放大图) 当Ki=80,Kp=0.006时,结果如图10所示。系统基本无震荡,整体输出电压基本保持500V,输出电压波形呈现为正弦波,可以看出全桥LLC谐振变换器状态稳定;当Ki=90,Kp=0.006时,结果如图11所示。输出电压震荡剧烈,输出电压在478-525V之间波动,因此可判定此时全桥LLC谐振变换器不稳定。仿真稳定范围为Kp=0.006,Ki≤80,与理论分析结果一致。 通过以上仿真,确认了基于Floquet理论的全桥LLC谐振变换器稳定性方法的可行性与准确性,并在确定电路基本参数的基础上,验证了全桥LLC谐振变换器控制参数稳定范围与理论分析结果相符。 本文针对全桥LLC谐振变换器闭环拓扑,首先通过扩展描述函数法构造闭环系统状态方程组,结合Floquet理论对Floquet乘子进行进一步推导,最后利用Floquet稳定性判据来判断全桥LLC谐振变换器在参考参数条件下的稳定性并配以仿真验证。得到如下结论: 1)利用Floquet稳定性判据对全桥LLC谐振变换器进行稳定性分析,其结果与传统稳定性分析方法结果相同。此方法与传统分析方法相比避免了建模及分析过程中高阶传递函数的求解,降低了稳定性分析的复杂程度。整体研究方法同样适用于不同电路参数或谐振变换器的稳定性分析情况。 2)对所选控制器的控制参数稳定范围进行分析并予仿真验证。在参考电路参数下:①固定比例控制系数Kp=0.006,则积分系数理论稳定范围为Ki≤80。②固定积分控制系数Ki=60,则比例系数理论稳定范围为0.001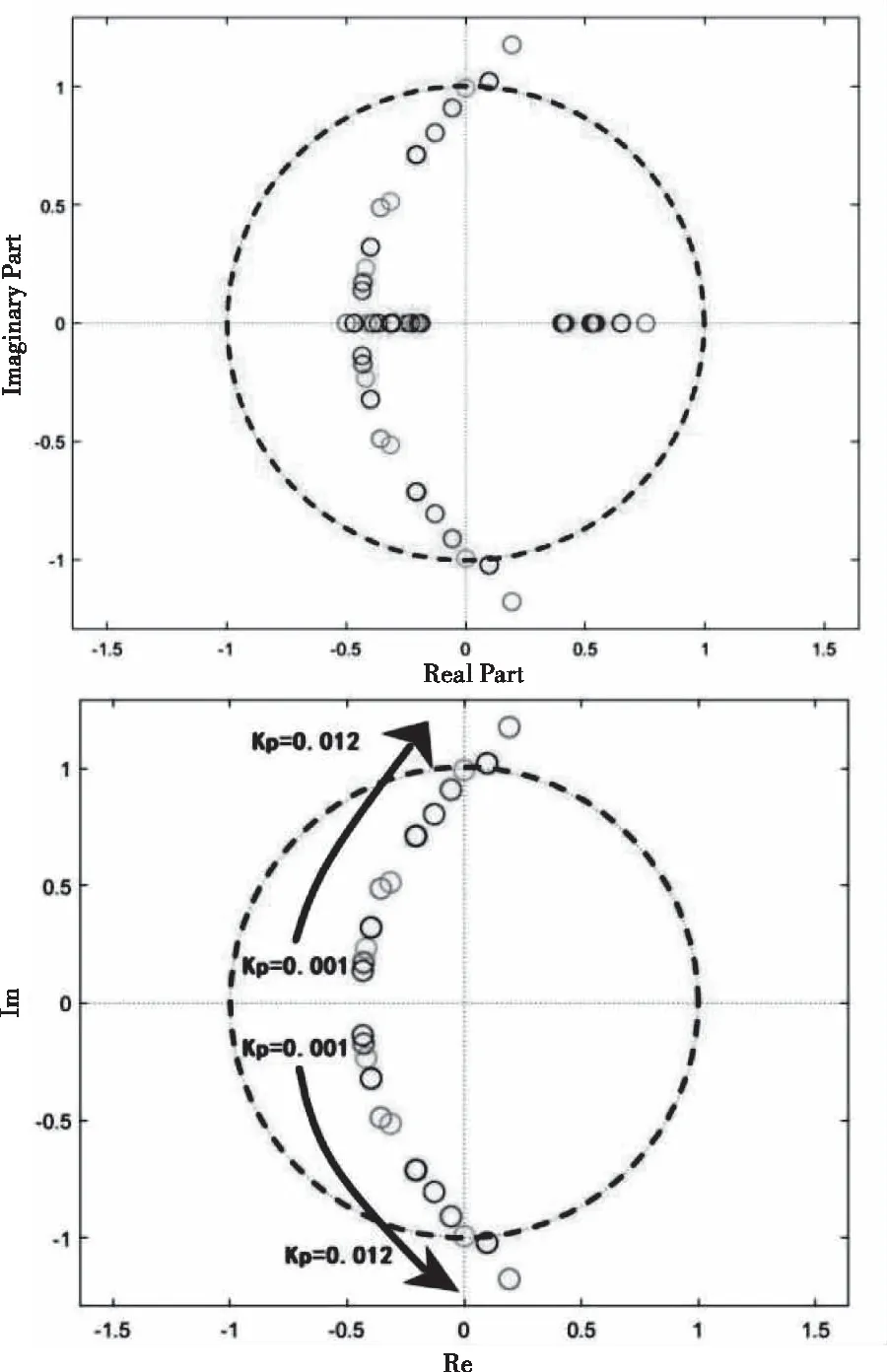
4 仿真验证
4.1 与传统稳定性分析比较
4.2 仿真结果验证

5 结论
