基于聚类和傅里叶基PSO-Elman谐波检测研究
2022-08-22杨静俭马鸿雁窦嘉铭
杨静俭,马鸿雁,2,3,窦嘉铭
(1. 北京建筑大学电气与信息工程学院,北京 100044;2. 建筑大数据智能处理方法研究北京市重点实验室,北京 100044;3. 智慧城市国家级虚拟仿真实验教学中心,北京 100044)
1 引言
电能作为一种清洁高效、传输便捷、易于控制的二次能源,在我国工业及制造业发展过程中占据了举足轻重的地位。近年来由于电力电子技术的迅速发展,大量电力电子器件应用于工业控制领域,导致负荷类型愈加复杂,所产生的谐波对电能质量的污染也日益严重[1]。为了保证频率、电压、电压波形畸变率和电压对称性四项指标上的电能质量,提高电力系统的稳定性和经济性,有源电力滤波器(Active Power Filter,APF)凭借其动态消除谐波、无并联谐振和拓展性强等特点已逐步取代传统LC滤波器成为谐波抑制装置发展的重要趋势[1-2]。
良好的动态响应和稳态精度是衡量APF性能的重要指标,因此谐波检测方法是实现谐波抑制的必要组成部分。传统的检测方法主要有基于瞬时无功功率理论的谐波检测法和基于傅里叶变换的谐波检测法,这些方法在精度或实时性方面存在一定缺陷[3-4]。随着数字化技术的发展,人工神经网络(Artificial Neural Network,ANN)在学术界掀起了革命性的浪潮,作为拥有得天独厚数字化优势的智能电网领域,神经网络为谐波检测与分析开辟了新的途径。文献[5]使用小波变换对信号特征进行特征分量提取,再与神经网络相结合对谐波的类型幅值和相位等参数进行了分析与检测;文献[6]对比多种算法优化下BP神经网络在不同性能上的差异,提出自适应遗传算法BP神经网络;文献[7]将均值滤波环节平滑权值波动的方法嵌入自适应神经网络单元,用于提高谐波检测精度;文献[8]根据电压幅值计算谐波补偿参考电流,从而对三相谐波神经元权值进行优化,经过权值优化后可以更好的计算滤波器输出电流和直流侧电容电压。文献[9]提出一种基于RBF神经网络的谐波检测法,与BP神经网络相比拥有更高的精度和实时性。本文从神经网络与谐波检测的基础出发,采用k-means聚类算法集成数据,根据聚类结果分类训练样本,采用粒子群优化算法(Particle Swarm Optimization,PSO)计算网络最优权值阈值,并构造适用于谐波检测的傅里叶基Elman神经网络。仿真结果表明,该算法比传统的神经网络拥有更高的收敛性和参数辨识精度,实时性也优于单纯的Elman神经网络。
2 谐波检测流程及数据制备
在供电系统中,交流电压及电流应为正弦工频波形,以电流为例,其表达式如式(1)所示
i(t)=Imsin(2πft+θ)
(1)
式中:Im为电流幅值;θ为初相角;f为频率。
由于电力系统中存在电感、电容、互感器、震荡器等非线性负载,当正弦电压施加于这些非线性电路时,电流就由正弦波畸变为非正弦波,非正弦电流将会在电力系统阻抗上产生压降从而使得电压波形也变为非正弦波[1]。考虑到电力系统是由双向对称元件组成,其电压和电流具半波对称特性,偶次谐波被抵消,故谐波检测时一般检测奇次谐波。因此电网中含有谐波分量的电流可以用傅里叶级数表示为

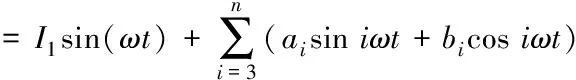
(2)
式中:Ii为第i次谐波的幅值,i=3,5,7…n;φi为第i次谐波的相位。
此外,该表达式中还存在ω=2πf、ai=Iicosφi、bi=Iisinφi的函数关系,因此可以根据ai和bi的值,按照式(3)和(4)来反推各次谐波的幅值和相位。
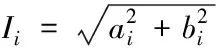
(3)

(4)
本文谐波检测思想即为通过建模辨识出待检测谐波中ai和bi,再利用式(3)和(4)计算幅值和相位,流程图如图1所示。
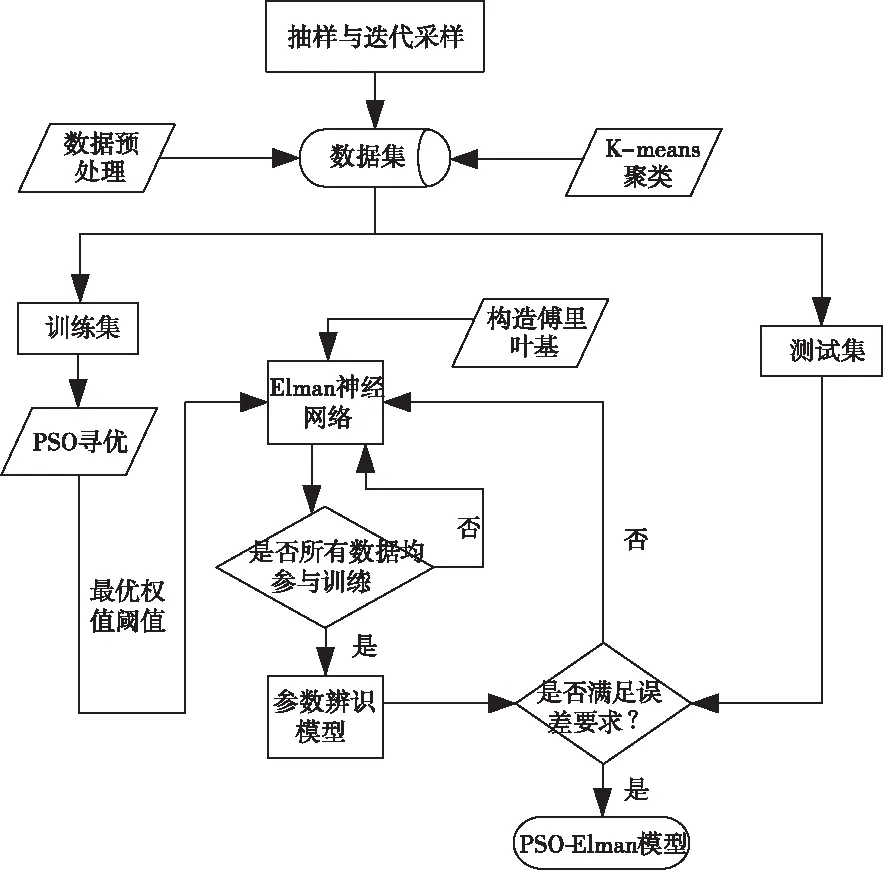
图1 谐波检测流程图
具体做法为:
1) 确定满足条件的ai和bi组合,将其作为神经网络的期望输出集。
2) 将每种组合分别代入谐波公式中,并对得到的谐波进行采样,即:
i(n)=I1sin(2πf/fs*T)

(5)

3) 将通过步骤1)和2)获得的数据集进行k-means聚类,将同类别的数据输入神经网络。
4) 通过PSO找寻最优的Elman神经网络参数,提升Elman神经网络训练性能。
电网中实际负载电流中谐波以3、5、7次谐波为主,以检测3次和5次谐波为例,当检测更高次谐波时,操作流程与此类似。含3次和5次谐波分量的电流为:
i(t)=sinωt+a3sin 3ωt+b3cos 3ωt+
a5sin 5ωt+b5cos 5ωt
(6)
输出集制备:按照电力系统的特点,3次和5次谐波的幅值不应超过基波幅值的50%,因此4个系数的取值范围可设为-0.5~0.5,步长设置为0.01。通过python对a3、b3、a5、b5进行排列组合,当抽样200000次并进行数据去重后,得到99633种组合形式,即样本的输出集为99633组。
输入集制备:与输出集相对应,训练样本也应为99633组,将每组(a3,b3,a5,b5)得到的谐波进行采样,得到输入集。由于这里检测的最高次谐波为5次谐波,根据Shannon采样定理,需满足fs>2f5,因此可取采样频率为1000Hz,故每个训练样本包含20个采样数值。
3 算法原理
3.1 傅里叶基Elman神经网络
Elman神经网络是在BP网络的基本结构上改进形成的,它在隐含层加入了一个承接层,达到了记忆的目的,使其对历史数据具有敏感性,加强了处理信息的能力。因此,Elman网络可以视作一个具有局部记忆和局部反馈连接的递归神经网络[10]。它的主要结构一般分为四层:输入层、隐含层、承接层和输出层。
隐含层激励函数通常取Sigmoid函数
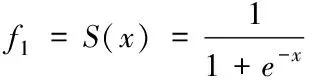
(7)
输出层传递函数选择purelin函数
f2=S
(8)
现对传统的Elman神经网络进行改造,将式(2)改写为矩阵形式可得

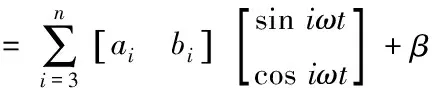
(9)
结合式(9),将基波分量视为偏置时构造傅里叶基Elman神经网络——Elman (FB),该神经网络隐含层中传递函数为正余弦函数对。傅里叶基Elman神经网络结构图如图2所示。
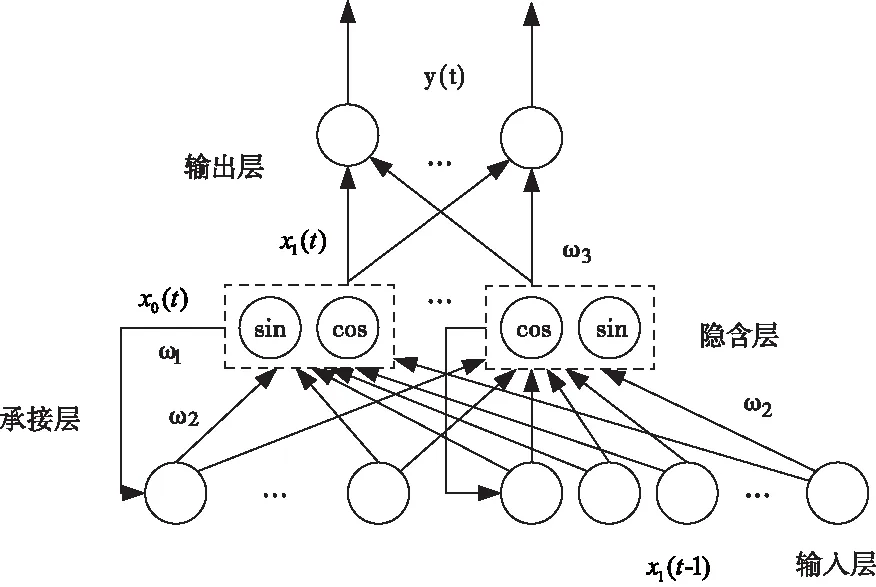
图2 Elman神经网络结构图
结合图2与激励函数可得隐含层输出为

(10)
因此网络输出计算公式为
Y(k)=ω3X1S+b2(k)S
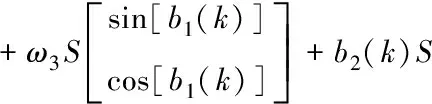
(11)
式中:ω1、ω2、ω3分别为承接层到隐含层、输入层到隐含层、隐含层到输出层的权值。b1、b2分别为输入层到隐含层、隐含层到输出层的阈值。
与BP网络相同,Elman神经网络所用的学习规则也为最速下降法,网络的权值和阈值通过反向传播进行调节,最终使得全局误差系数达到最小值,其学习的本质就是对各个连接权值进行动态调整。虽然在计算能力和网络稳定性上优于BP网络,但由于学习规则相同,其训练过程中仍易出现收敛慢和陷入局部最优的缺点,难以达到全局最优解。针对Elman神经网络的不足,本文采用全局优化算法中的粒子群优化算法提升训练效果。
3.2 粒子群优化算法基本原理
粒子群优化(PSO)算法是基于模仿鸟类觅食行为发展的一种随机探索优化算法,其基本思想是通过粒子间协作和信息共享来寻找最优解[11]。每个粒子都是待优化空间的潜在解,将一群粒子初始化,根据评价各微粒的目标函数确定某时刻各微粒经过的最佳位置和群体发现的最佳位置,如此迭代循环发掘最优解。每一次迭代中,通过跟踪式(12)和式(13)来更新各微粒的速度和位置[12]。
vi,j(t+1)=vi,j(t)+c1r1[pi,j-xi,j(t)]+
c2r2[pg,j-xi,j(t)]
(12)
xi,j(t+1)=xi,j(t)+vi,j(t)
(13)
式中:c1和c2为加速常数,也称学习因子;r1和r2为0到1之间均匀分布的随机数。
由于粒子群优化算法具有调整参数少、可以全局和局部寻优、算法实现简单、收敛较快等优点,因此在神经网络训练、模糊控制和多目标优化方面有着广泛的应用。
3.3 k-means聚类算法基本原理
k-means聚类算法是以数据点到聚类中心的某类距离作为优化的目标函数,将数据样本进行分类与集成的统计分析方法。其一般步骤为[13]:
1) 随机筛选K个点作为数据样本的初始聚类中心。
2) 计算每个数据点到K个聚类中心的欧式距离,根据距离的大小将数据点分到不同簇中。即计算
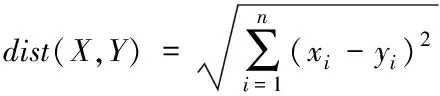
(14)
3) 求解每个簇的均值向量,用于更新K个簇的聚类中心。
4) 循环迭代步骤2)和3),当聚类中心不再改变时完成聚类。
在谐波参数辨识中,不同谐波采样数值之间的既有差异性也有相关性,所以找寻数据之间的内在相似性可以减小差异性带来的不良影响。k-means聚类算法可以找出谐波之间的相似性并进行合理的集成分类,所以,利用该算法分类数据后再进行神经网络预测模型的训练。

图3 参数b3网络输出误差仿真图
4 仿真分析
4.1 神经网络建模及仿真分析
对本文改进的傅里叶基Elman神经网络预测模型进行建模,输入层节点n=20,输出层节点m=4;由于隐含层中神经元个数与训练精度和计算复杂度有关,因此结合实际情况本文选取隐含层中神经元个数为15;最大训练次数设置为5000次,网络学习速率设置为0.05,目标误差为0.65×10-3。对于共计99633组数据,本次实验选取前80000组为训练集,余下的19633组做测试集。
使用傅里叶基Elman神经网络进行参数辨识的仿真结果如图4和图5所示。图3为测试集中19633组谐波系数的实际值与 网络输出值之间的误差(以b3为例)。Elman神经网络的预测模型训练结果如图4所示,其为网络输出值与实际值对比图,由于数据量较大导致图像过于密集难以进行分析,因此图4中为输出前800组预测结果。
通过图4可以看出,傅里叶基Elman神经网络预测效果良好,网络输出曲线与实际值曲线基本吻合。但图3网络输出误差也能体现出网络对b3预测误差相对较大。进一步对4个参数的预测精确度进行计算并取10次平均值可得:a3的网络预测精确度为97.32%、b3为96.53%、a5为96.97%、b5为96.64%。
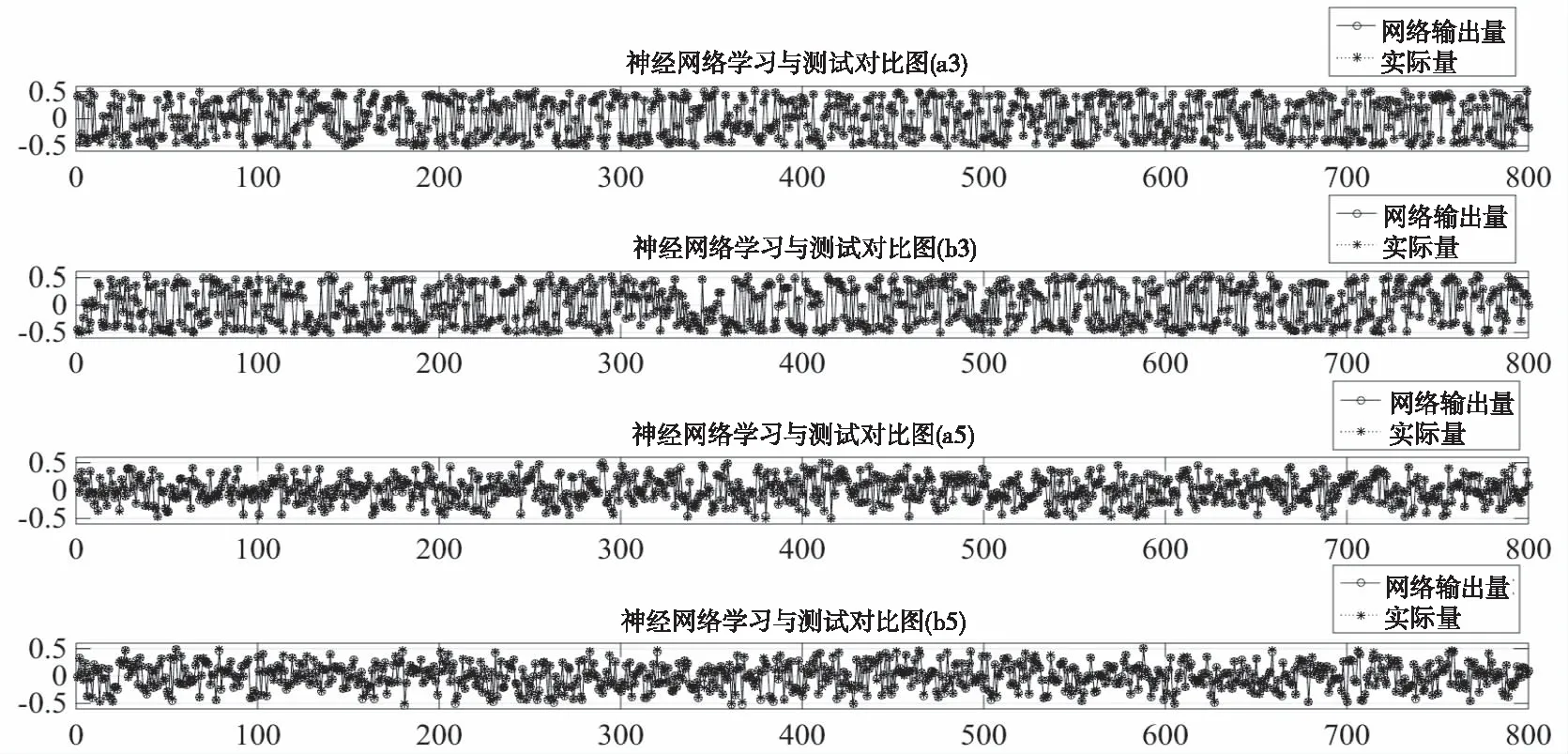
图4 傅里叶基Elman神经网络输出值与实际值对比仿真图
根据均方误差下降曲线来分析神经网络训练时的表现,从图5可以看出,经过208次迭代模型达到了收敛精度,且在110次迭代之前误差下降迅速,之后网络表现进入曲线平坦区,延长了收敛时间。由于谐波检测算法的速度直接影响APF的动态性能,为了提升收敛速度和预测精度,通过k-means聚类对训练数据进行集成,将聚类在同一簇的数据用于网络训练;并采用PSO优化算法找寻最优的初始权值和阈值赋予神经网络提升检测表现。输入输出集通过k-means及PCA降维进行K=4的聚类,前1000组数据可表示为图6。
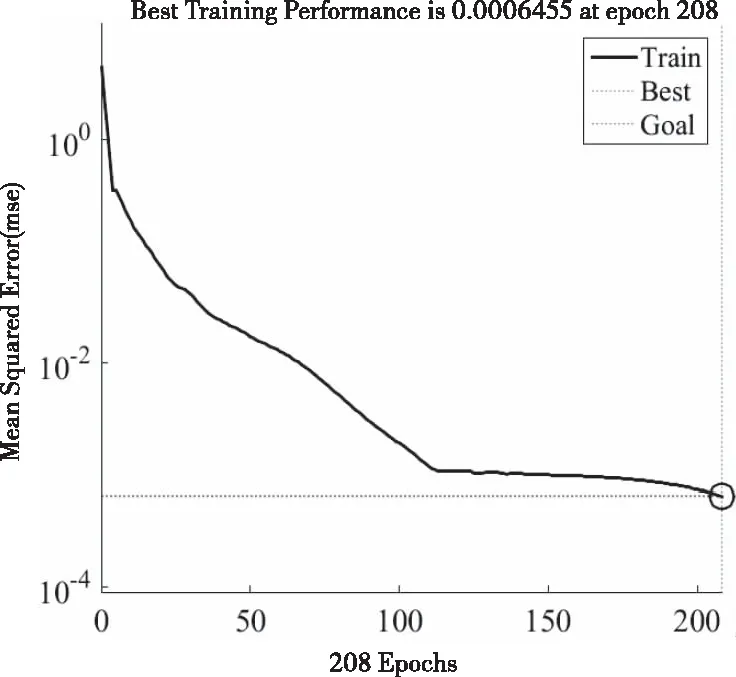
图5 神经网络误差(mse)下降曲线

图6 训练数据聚类结果
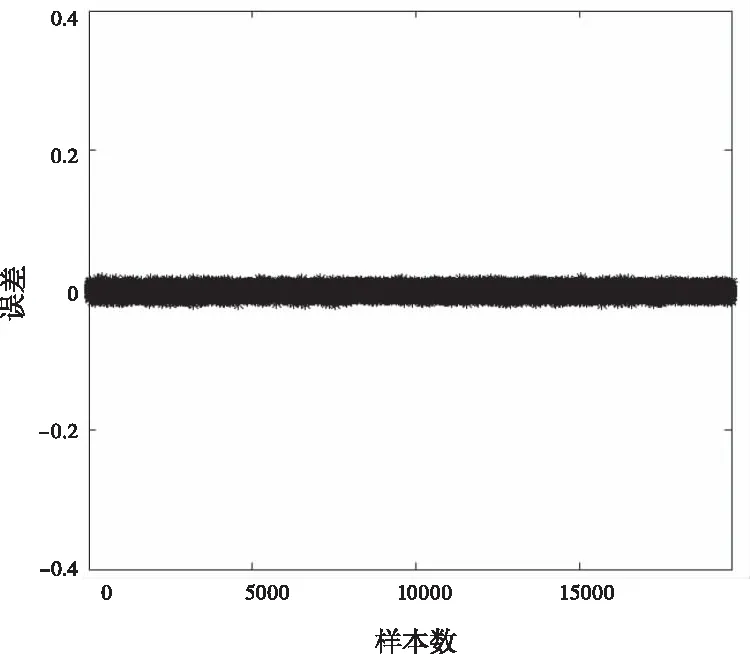
图7 k-means及PSO优化后参数b3网络输出误差仿真图
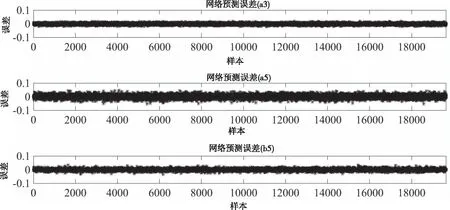
图8 优化后参数a3、a5、b5网络输出误差仿真图
PSO参数方面:将种群个数设置为20,进化代数为100,惯性因子为0.8,加速因子c1和c2均设为1.49445。使用k-means及PSO改进后的四个参数的网络输出误差如图7和图8所示;谐波参数辨识误差对比参见图9。

图9 各模型输出误差对比(b3)
从图9可以看出本文提出的融合k-means的傅里叶基PSO-Elman神经网络在表现较差的参数b3辨识精度方面有了显著提高,以前300个输出为例,最大误差幅值下降约50%。对比图3与图7也可以看出,b3预测误差图的宽度明显变小,这说明检测精度有所提升。通过分析图8可知,其它三个参数的预测误差也均在±0.1之间。说明该算法结合了k-means及PSO的优点,使整个训练过程在数据分类处理和网络参数寻优方面都得到了优化,提升了神经网络的网络性能与预测表现。
分析表1可知,重置为傅里叶基的Elman网络RMSE下降一个数量级,结合聚类与PSO算法后进一步下降;根据表2中的实验结果所示,本文提出的方法表现最好。

表1 不同ANN检测方法均方根误差对比
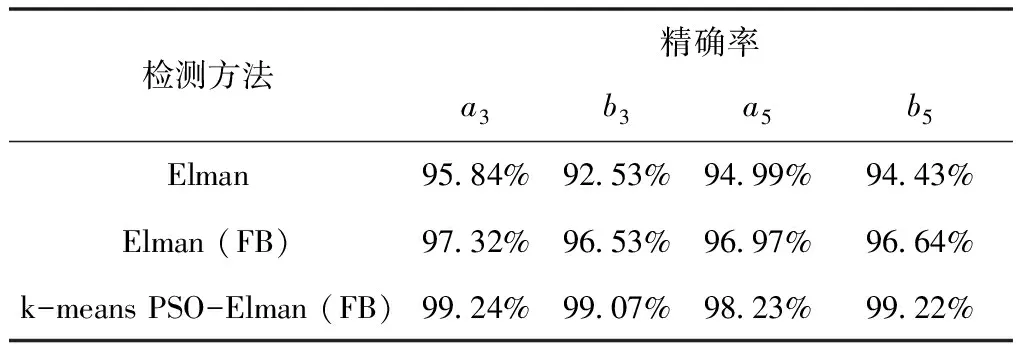
表2 不同ANN检测方法精确率对比
4.2 电路仿真与分析
上一节仿真分析已经证明本文提出的检测方法具有较高精度,为验证基于k-means聚类和傅里叶基PSO-Elman谐波检测方法在实际电路中的有效性,采用Matlab/Simulink搭建电路模型进行仿真。
搭建如图10所示仿真主电路。三相电源对称,相电压220V,频率50Hz;三相不可控整流桥带阻容性负载模拟导致电网电压畸变的非线性谐波源;负载方面采用不控整流桥带电阻模拟非线性负载[14]。示波器中A相相电流如图11所示。
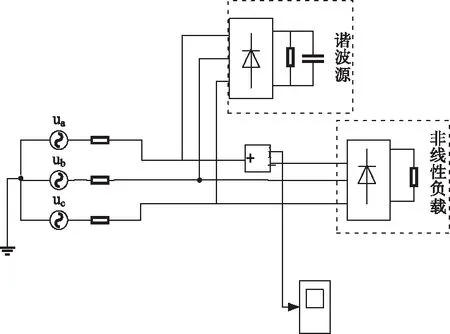
图10 仿真主电路
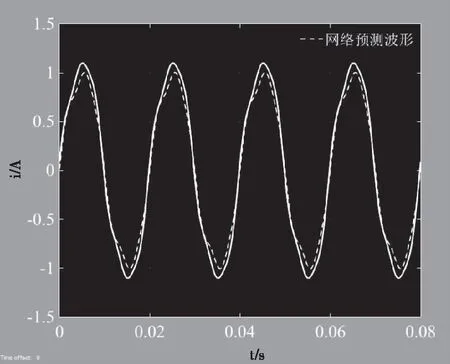
图11 A相相电流波形图
通过powergui模块设置信号类型为离散,采样时间设为0.001s从而完成对该电流波形的20次采样。将得到的20个采样点数值输入到训练好的网络模型中,得到a3,b3,a5,b5的值分别为:0.0536、0.0472、0.0325、-0.0295。再通过式(3)、(4)折算出各次谐波的幅值和相位,可得网络预测的含有谐波成分的信号为:
i(t)=sinωt+0.072sin(3ωt+41.38°)
+0.044sin(5ωt-42.23°)
(15)
上述网络预测所得信号的波形如图11虚线所示,对比示波器输出波形(实线)可知该信号在幅值、相位与变化趋势上基本与实际电流波形相吻合,说明本方法对电网谐波有较好的检测能力。
在搭建实际电路仿真模型中发现,当电流幅值过大和5次以上谐波分量过多时,网络预测准确性下降。原因在于式(6)中仅含有基波和3次、5次谐波,且基波幅值为1,这就导致训练数据存在多样性不足的问题,未来可以通过补充不同幅值和谐波次数时的训练数据来提高网络预测精度。
5 结论与展望
本文重置Elman神经网络激活函数,结合粒子群优化算法并采用k-means聚类算法减少数据差异性的影响,针对谐波检测问题提出了谐波参数的k-means PSO-Elman(FB)辨识方法。该方法改进了传统BP神经网络动态记忆缺失的缺点,同时也克服了Elman神经网络同样容易陷入局部最优、收敛缓慢的问题,使其更适用于动态变化的电网谐波检测中。仿真结果表明,使用此方法时4个谐波参数的辨识精度均达到98%以上,与单纯的Elman神经网络相比,误差幅值也有明显下降,说明该方法能够较好的实现谐波参数的辨识。通过物理验证也能反映此方法的可行性与准确性。未来可以补充不同特征的谐波采样数据,建立包含不同电压等级、谐波次数和间谐波的网络训练集,以更好的满足谐波检测对准确性和实时性的要求。
