高轨辐射源被动雷达空-时积累海面动目标检测技术

张 蓉 黄 川 李中余 武俊杰 杨建宇

（电子科技大学信息与通信工程学院，四川成都 611731）

1 引言

随着电子干扰技术的发展、反辐射导弹性能的提高、隐身武器的使用以及低空突防能力的提高，给雷达系统的生存和作战能力带来了挑战，而双（多）基雷达利用其收发分置的工作模式，具有抗干扰能力强、抗摧毁能力强、反隐身以及抗低空突防能力强等特性。同时，收发分离的模式可以根据不同的军事需求，在收发装置的数量以及部署平台上提供了多种组合的可能性［1-7］。被动雷达是双（多）基雷达的一种特殊形式，其以环境中已存在的辐射源作为系统辐射源，接收站被动接收目标所反射的回波信号。目前主要研究的辐射源信号有调频（FM）信号［8-10］、数字音频广播（DAB）［11-12］、地面数字视频广播（DVB-T）［13］等。地面辐射源可以提供相对较高的功率密度，但其覆盖区域局限于陆地区域。天基辐射源以卫星作为辐射源平台，具有覆盖范围广、不受地面疆界限制、工作状态稳定等优势，可以应用于大部分场景［14-15］。

全球卫星导航系统（global navigation satellite system，GNSS）、低轨通信卫星星座（如Iridium）和地球同步轨道合成孔径雷达（geosynchronous earth orbit synthetic aperture radar，GEO SAR）卫星等典型卫星系统都可以作为被动雷达系统的潜在辐射源。其中，地球同步轨道卫星具有高达约36000 km 的轨道高度［16］，其单颗卫星覆盖面积可达地球表面的近三分之一，远大于中低轨卫星的单星覆盖率。此外，GEO SAR 辐射源具有相对较高的信号带宽与地面功率密度［17］，可获取更优的回波信噪比与距离分辨率，在被动雷达领域具有良好的应用前景。

目前，关于高轨辐射源被动雷达的研究主要集中在地面静止场景成像上，即通过由高轨辐射源GEO SAR卫星和机载接收站组成的GEO双基SAR系统实现GEOSAR成像。GEO-SAR在系统性能、设计以及成像算法等方面已经有了较为深入的研究［18-22］。由于GEO SAR卫星（以下简称GEO卫星）的覆盖范围广泛，能够突破地面辐射源的限制，因此高轨辐射源被动雷达在动目标检测，尤其是海面运动目标探测方面具有应用潜力，但目前未见相关研究。

为了实现有效的海面运动目标探测，本文构建了一种由GEO 卫星发射机和多个接收站组成的高轨辐射源多基被动雷达系统。与一发一收的双基构型相比，多个不同位置接收站构型提供了两个优势：（1）多基回波融合，可提高目标信噪比并抑制目标的雷达截面积（radar cross-section，RCS）闪烁，有益于提高目标检测性能；（2）多基构型为系统提供了目标定位的能力。然而，接收站空间差异性导致回波具有不同的距离历史与多普勒参数，因此，多基融合存在困难。

目前针对一发多收构型雷达已有相关研究。文献［23］针对地面辐射源提出了一种一发多收的被动雷达构型，并通过多站回波融合，获取运动目标的位置信息和速度信息，实现运动目标稳定跟踪；然而，该方法局限于地面辐射源，在需以卫星信号为辐射源的场景下，长时间的回波积累将导致该方法在目标探测时存在不可忽略的能量散焦问题。文献［24］以导航卫星作为辐射源，通过阵列天线被动接收目标区域所反射的机会信号，将不同天线单元所接收到的目标回波进行多普勒频率及相位补偿后，完成多天线间回波融合。然而，该方法忽略了阵列天线间的时延差异，且多普勒补偿方法仅对天线阵列分布可行。

本文提出了一种基于空-时联合积累的高轨辐射源多基被动雷达海面运动目标检测技术。首先，为了解决单个回波在观测时间内跨距离单元与跨多普勒单元问题，采用Keystone 变换和去调频傅里叶变换对各站回波进行处理，将各站能量积累到多普勒参数域。然后，为了解决多基间目标距离和多普勒参数的差异性问题，我们根据目标角度、距离、多普勒参数与多基构型间的解析形式，建立各站目标回波域、多普勒参数域间各自映射关系，完成多基间目标回波能量的对齐。最后，将多基回波进行融合，实现信噪比的有效提升，进而实现高轨辐射源被动雷达动目标的检测和定位。

2 回波建模与特性分析

2.1 目标回波模型

本文构建了一种由GEO 卫星辐射源和多个机载接收站组成的高轨辐射源多基被动雷达系统，该系统中每一个接收站均配备有两个天线。其中，监视天线指向探测区域用于接收动目标反射的回波信号，而参考天线指向GEO 卫星用于获取直达波信号，用于实现收发平台间的信号同步。

如图1 所示，以观测场景中一固定点为原点构建东北天坐标系，其中X轴、Y轴和Z轴分别代表东向、北向和天向。动目标、卫星和第n（n=1，2，…，N）个接收站的位置在该坐标系中分别描述为PTg=[XTg，YTg，ZTg]、PT=[XT，YT，ZT] 和PR，n=[XR，n，YR，n，ZR，n]，卫星和第n个接收站的运动速度分别为VT和VR，n，目标的运动速度为VTg=[vx，vy，0]，RT和RR，n分别表示GEO卫星和第n个接收站到动目标的距离，Rb，n表示GEO 卫星距第n个接收站的距离，由于目标、卫星和接收站的运动，上述距离随时间不断变化。

GEO 卫星发射线性调频脉冲信号对地面进行照射，其发射信号可表示为：

其中，rect(·)为矩形窗，t表示时间，T表示脉冲宽度，K表示信号调频率，fc表示信号载波频率。GEOSAR卫星信号地面功率密度约为-69.7 dBW/m2。

解调后的第n个接收站对应的直达波信号在二维时域可表示为：

其中，τ为距离向时间，η为方位向时间，Ta表示对目标的总观测时长，c表示光速。

同样，第n个接收站的监测天线接收到的动目标回波信号可表示为：

其中，A0为目标回波幅值。

将目标回波与直达波进行互相关处理，完成信号同步，并实现回波信号距离向脉冲压缩，其结果表示为：

其中，A1表示回波的脉压后的幅度，λ为信号波长，Rn(η)=RT(η) +RR，n(η) -Rb，n(η)。

由于卫星发射源与目标的运动，双基距离历史随方位向时间变化。将第n个接收站的双基距离历史Rn(η)在参考时刻（即η=0）沿方位向时间进行二阶泰勒展开，得到：

其中，R0，n为参考时刻的双基距离分别为多普勒质心（Doppler centroid，DC）和多普勒调频率（Doppler frequency rate，DFR）。故方位多普勒频率可以表示为：

其中，

由式（5）和（6）可知，距离和多普勒频率均存在跨单元现象。下文中通过仿真对跨距离单元和跨多普勒单元现象进行了描述。

2.2 特性分析

由于高轨辐射源多基被动雷达系统设置了多个接收站，与采用单个接收站相比，将长观测时间内多站回波相结合，能有效增加信噪比，有益于提高目标检测的可靠性。

在观测时间内，由于辐射源与目标的运动，双基距离历史随方位时间变化，造成目标回波跨距离和多普勒单元现象。此外，多个接收站的位置差异导致不同接收站之间距离和多普勒参数的差异，造成了多基回波融合的困难。

假设目标与接收站分别以速度（14.14，14.14，0）kn 和（0，200，0）m/s 做匀速运动，GEO 卫星信号带宽为100 MHz［25］，由五个不同接收站接收目标回波，则不同回波的距离历史和多普勒频率如图2 所示。图2（a）展示了多个接收站目标回波距离历史，对于单站回波，动目标的信号回波存在较大的一次项距离徙动，且不同接收站之间存在不可忽视的距离参数差异。图2（b）为位置互不相同的多个接收站动目标多普勒频率变化曲线。每个接收站动目标存在不可忽略的多普勒徙动。同时，不同位置的接收站动目标多普勒参数存在差异。

3 基于空-时联合积累的海面运动目标检测技术

本文提出了一种基于空-时联合积累的高轨辐射源多基被动雷达海面运动目标检测技术，以实现距离徙动和多普勒徙动的校正以及距离和多普勒参数的补偿，该技术由时间积累和空间积累两个步骤组成。

3.1 长时间回波能量积累方法

为解决观测时间内回波的距离徙动和多普勒徙动问题，本文采用Keystone 变换和去调频傅里叶变换对目标回波能量的距离徙动和多普勒徙动进行矫正，并将各站目标回波能量积累到多普勒参数域。

将第n个接收站的二维时域回波进行距离向傅里叶变换，得到距离频域-方位时域回波，表示为：

其中，A2为常数，fτ表示距离频率。

采用Keystone 变换方法，通过仿射变换η=fc/(fc+fτ)ηm（ηm表示新的方位时间变量）去除一阶耦合（二阶距离徙动可忽略），将第n个接收站目标回波通过逆傅里叶变换到二维时域的结果表示为：

从该结果中提取同一距离单元的方位信号，若该距离单元包含目标，则取出的方位信号包含全部目标能量，为了描述方便，下文中仍然用η表示新的方位时间变量ηm，该方位信号可表示为：

由于多普勒调频率的存在，该信号在多普勒频率域存在跨单元现象，本文中利用去调频傅里叶变换来实现多普勒徙动校正。去调频傅里叶变换的形式，表示为：

其中，fη表示多普勒频率。

由式（10）与（11）可知，若对该方位信号进行去调频傅里叶变换，当时可将信号全部能量在多普勒频率域聚集到一点（即），实现最优的目标积累效果。因此，通过该处理可将第n个接收站目标回波信号在多普勒调频率-多普勒质心域内积累到处。

3.2 多基空间积累方法

为了完成多基目标回波的高精度融合，需对多基间距离参数和多普勒参数进行差异性补偿，根据目标角度、距离、多普勒参数与多基构型间的解析形式，能够在各站目标回波域、多普勒参数域间建立各自映射关系，实现多基间目标回波能量的对齐和积累。

首先，为了补偿各站回波间距离参数的差异，假设目标与第n接收站的距离在地面投影为Rp，n，令，通过搜索波达方向（Direc⁃tion of Arrival，DOA）ϕ，得到目标位置。将第1 个接收站作为参考接收站，根据卫星辐射源，目标以及参考接收站之间的空间几何关系建立方程：

对上述方程进行求解，得到：

由的定义以及其余接收站位置坐标可以实现各站回波双基距离的补偿。

然后，为了补偿各站回波多普勒参数的差异，对参考接收站目标回波在多普勒参数域中的每一个离散值点(fdr，fη)，建立方程组：

根据解出的目标速度以及卫星位置和运动参数等对其余各站回波在多普勒参数域的积累结果分别进行DFR 补偿和DC 补偿。利用解出的目标速度、卫星参数以及第n个接收站的参数，根据公式（7）可得第n个接收站目标回波的多普勒调频率fdr，n和多普勒质心fdc，n为：

进而对第n个接收站目标回波的长时间积累结果进行多普勒参数补偿，即：

最后，将补偿后的多基回波信号求和完成多站融合，则所有接收站的融合结果表示为：

4 仿真实验与结果分析

综上所述，本文提出的基于空-时联合积累的高轨辐射源多基被动雷达海面运动目标检测技术流程如图3所示。

本节对基于空-时联合积累的高轨辐射源多基被动雷达海面运动目标检测技术进行了仿真验证。仿真实验中以GEO 卫星为辐射源，假设动目标的运动状态为匀速运动，设置了五个机载接收站，仿真实验参数如表1。

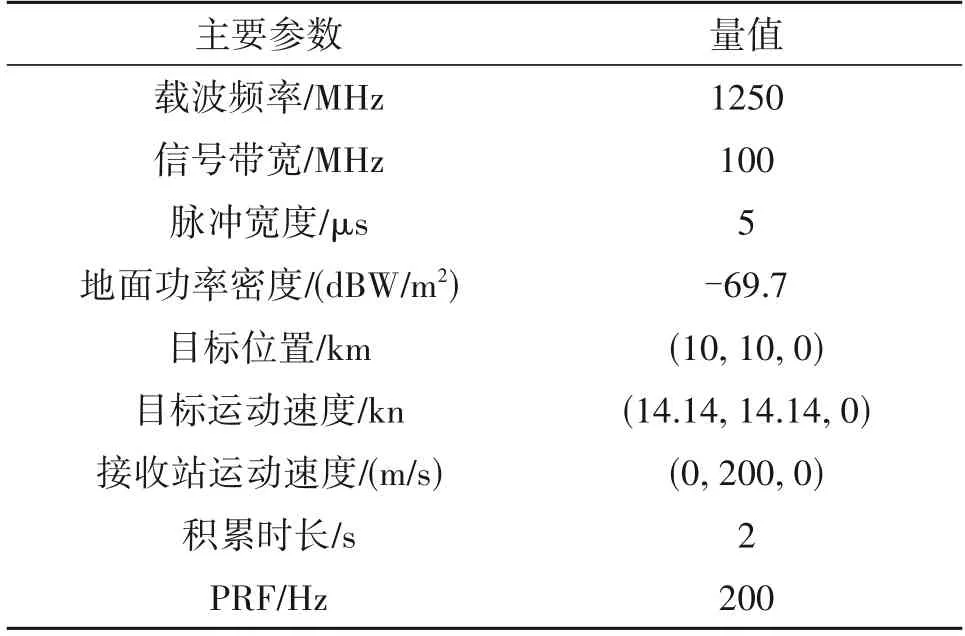
表1 仿真参数Tab.1 Simulation parameters

将高斯白噪声作为干扰背景，所得距离脉冲压缩前的接收信噪比为-31.90 dB，不满足目标检测所需信噪比。图4为距离脉压后动目标距离单元在方位时间维的结果，此时目标被噪声淹没。为了有效增强信噪比，提高检测性能，下面利用本文所提出的技术对动目标回波进行处理。

首先，利用Keystone 变换对观测时间内目标回波的距离徙动进行校正，将目标回波聚集到同一距离单元内。并通过去调频傅里叶变换去除回波跨多普勒单元现象，将回波积累到多普勒参数域。图5 为第1 个接收站目标回波经过时间积累后多普勒参数域的二维图像，可以明显看到图中有一个孤立的峰值，回波能量得到有效积累。

以第1 个接收站目标回波为参考进行位置估计，若估计DOA 值恰为真实值，则根据估计所得的目标位置可补偿其余接收站目标回波的双基距离。其余四个接收站的动目标回波在多普勒参数域的二维图像，如图6 所示。通过对比不同接收站之间的回波积累结果，可以发现不同接收站目标回波DFR、DC均存在差异。

为了补偿上述差异，根据目标速度与多普勒参数的映射关系，利用参考接收站目标回波积累结果求解目标速度，并结合目标与接发平台的位置信息及运动参数，分别对其余接收站目标回波的多普勒参数进行补偿，补偿后各站回波多普勒参数二维图像如图7所示。

最后将补偿后的多个回波信号求和完成多基回波融合。图8为将多基回波融合后多普勒参数域示意图，可以观察到，多个回波信号的能量集中到一个孤立峰值处，证明所提出的技术将多个接收站目标回波信号进行了有效融合。

为了清楚地展示该技术在检测性能方面的优势，将虚警率设置为10-4，分别对单站回波和多站回波在不同信噪比下的检测概率进行测试。图9展示了以单站（平均）信噪比为变量的检测概率函数，红线和蓝线分别表示单站检测概率轨迹和多站检测概率轨迹。显然，增加接收站的数量使得检测概率得到了明显提升。因此，通过适当利用多个接收站同时接收信号，可以获得较大的积累增益，从而检测到单接收站双基构型下长时间积累也无法观测到的目标。

为了展示多基构型下高轨辐射源被动雷达系统的定位能力，本文设置了不同的波达角度和双基距离，对多基构型下动目标回波信号进行仿真，经过回波融合后不同波达角和双基距离下得到的积累峰值如图10 所示，可以看出，仅当波达角度为78.7°，且双基距离为36295.9 km 时峰值达到最大，即最优积累效果仅在目标位置处可达，证明了通过该雷达系统可以实现动目标定位，动目标位置坐标仿真结果为（9.999，10.001，0）km，与预设真实值相符。

5 结论

本文提出了一种由GEO 卫星发射和多个平台被动接收的高轨辐射源多基被动雷达系统，用于实现海面运动目标的有效探测。与一发一收的双基构型相比，多个不同位置接收站构型提供了两个优势：（1）多基回波融合，可提高目标信噪比并抑制目标的雷达截面积（radar cross-section，RCS）闪烁，有益于提高目标检测性能；（2）多基构型为系统提供了目标定位的能力。然而，接收站空间差异性导致回波具有不同的距离历史与多普勒参数，因此，多基融合存在困难。本文针对高轨辐射源多基被动雷达系统在海面运动目标探测上的应用，提出了一种基于空-时联合积累的海面运动目标检测技术。该技术校正了各站动目标回波跨距离单元和跨多普勒单元现象，补偿了多基回波距离参数和多普勒参数的差异，实现了多基回波的高精度融合，有效提高了检测信噪比。通过仿真结果，验证了该检测技术的有效性，实现目标检测并实现动目标的定位。