基于ADMM的低仰角目标二维DOA估计算法
2022-08-19马健钧魏少鹏刘宏伟
马健钧 魏少鹏 马 晖 刘宏伟
(西安电子科技大学雷达信号处理国家重点实验室 西安 710071)
1 引言
随着隐身技术、低空突防和防辐射导弹等一系列反雷达技术的发展,已对现有雷达技术的发展提出了严峻的挑战。米波雷达具有波长较长、穿透能力强的特点,在反隐身和抗辐射导弹等方面具有独特的优势,特别是在隐身目标远程警戒任务中,米波雷达能够实现目标的探测和跟踪,并为防空预警系统提供目标3坐标信息,从而引导我方武器系统对目标进行摧毁和拦截,因此受到世界各国的广泛重视[1–3]。随着应用需求的不断提升,现代米波雷达应具有高精度测距和2维测角能力。然而,米波雷达在对低空、超低空目标进行探测时,雷达接收回波信号不仅包括由目标散射的直达波信号,而且还存在经地面反射的多径信号。多径信号的存在将导致传统DOA算法性能下降,甚至失效,其主要原因可总结为以下3个方面:(1)直达波和多径信号通常位于同一距离单元,难以从时域、频域进行分辨。(2)由于波束宽,直达波和多径反射波处于同一波束宽度甚至半波束宽度内,且为一组强相关信号,严重影响了米波雷达测角精度。(3)米波雷达带宽较窄,距离单元一般在百米量级,距离测量精度进一步影响了雷达测高性能。
近年来,众多国内外学者对米波低仰角DOA问题展开大量研究。现有低仰角DOA方法主要分为特征子空间类算法、最大似然(Maximum Likelihood, ML)类算法和压缩感知类算法。低仰角特征子空间类算法主要是以多重信号分类(MUltiple SIgnal Classification, MUSIC)和旋转不变子空间(Estimation of Signal Parameter via Rotational Invariance Technique, ESPRIT)为框架的求解方法。由于MUSIC算法较ESPRIT算法有更高稳定性和角分辨率,因此受到研发者的青睐[4,5]。文献[6]采用空间平滑(Spatial Smoothing, SS)技术恢复协方差矩阵的秩实现解相干,但有效孔径的缺失将会导致算法估计性能的下降,使得该类算法难以满足米波雷达实际应用需求。文献[7]将交替投影(alternating projection)技术与MUSIC算法相结合,利用先验信息可实现低仰角估计,但由于其代价函数是一个非凸的优化问题,不总能保证算法收敛到全局最优解。ML类算法可直接处理相干信号,在低信噪比条件下也具有较好估计性能,但算法计算量随着目标个数呈指数增长,运算量巨大,无法满足实时性需求[8]。压缩感知类算法利用目标在空域的稀疏特性,可直接进行相干源DOA估计,且大多数稀疏重构类DOA估计方法,在少快拍、低信噪比条件下有更好的估计性能[9–11],但目前稀疏重构类DOA估计算法通常运算量较大,如何在不降低算法精度的前提下降低算法计算量一直是该类算法的研究热点。交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)可将具有可分结构的凸优化问题分块处理,降低求解复杂度。由于其估计精度高,收敛速度快的优势被广泛应用在信号处理、图像处理、机器学习等各领域中[12–15]。
本文将ADMM算法推广到面阵2维角度估计中,并提出适用于米波面阵雷达的2维DOA估计算法。该算法首先通过2维波束合成对目标角度进行粗略估计,其次利用方位、俯仰角无耦合的特性,对面阵数据分别进行行、列波束合成,并通过傅里叶插值的方式提取目标数据,最后利用ADMM算法进行方位、俯仰角估计。相比于传统算法,本文方法利用角度粗估计信息,限定了目标角度范围,减少了求解运算量,同时通过行、列波束合成处理在提升信噪比的同时实现数据降维,避免了2维联合估计复杂计算量,提高了运算效率。仿真结果验证了所提算法的有效性。
2 信号模型

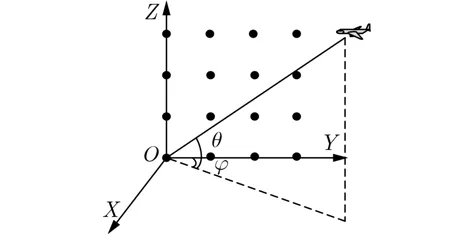
图1 米波面阵雷达几何模型
达越远,多径入射角绝对值和直达波入射角差值越小。


图3 角度差值与目标距离关系


确定稀疏约束函数后,通过稀疏恢复算法即可求解出目标方位、俯仰角。
3 基于ADMM的2维DOA算法
3.1 ADMM算法
ADMM是一种适用于求解分布式优化问题的计算方法,其最显著的优点是能够对变量进行分离处理,并且充分利用目标函数的可分离结构,求解收敛速度快,易于工程实现。求解式(12)目标函数可看成是LASSO类稀疏重构问题,将ADMM算法应用于LASSO类最优化稀疏问题中,其运行速度和重构精度优于其他主流的L1范数方法[17,18]。
根据式(12)可知,对目标函数的求解可看成是角度变量的优化问题,ADMM解决两变量含等式约束的优化类问题一般形式可表示为

3.2 2维DOA算法实现


综上所述,基于ADMM 2维快速DOA估计方法处理流程,如图4所示。

图4 本文算法流程图
3.3 算法复杂度分析


4 实验仿真并分析
本节通过与DBF[1],SS-MUSIC[6]和AP-MUSIC[7]算法在DOA估计精度及运算时间方面的对比,验证所提算法的有效性。仿真条件设置如下:水平阵元个数20,竖直阵元个数16,阵元间隔0.5 m,波长1 m,雷达架高10 m,镜面反射系数为0.95,各阵元发射带宽500 K。采用均方根误差(Root-Mean-Square Error, RMSE)作为DOA估计精度的衡量标准,方位、俯仰角RMSE可分别定义为

实验1 为验证本文所提算法的有效性。假定目标距雷达50 km,目标高度为1350 m,根据图2空间几何模型可计算得到目标俯仰角约为1.5°,设定目标方位角为30°。图5为信噪比5 dB时,参考行、列阵元波束合成结果。实验设置行列波束合成角度搜索间隔为1°,由图5(a)可知,通过方位波束合成可知目标方位角度在30°附近,因此可通过波束合成确定目标粗略方位角度。但对于俯仰角来说,由于直达波和多径信号俯仰角度近似满足θd≈-θs,通过波束合成目标对应的角度在0°附近,如图5(b)所示。通过波束合成可确定目标大致位置,因此可根据阵列方位、俯仰角对应波束宽度设定方位、俯仰角搜索范围。本实验中设定为方位搜索范围为 28°~32°, 俯仰角搜索范围可设定为- 5°~5°,角度搜索间隔设置为0.1°。图6为本文所提算法与DBF, SS-MUSIC和AP-MUSIC算法正确估计时空域谱结果,从图6(a)可以看出DBF虽然可以正确估计目标方位角度,但相比于其他3种方法,其估计精度较差,不具有超分辨性能。从图6(b)可以看出由于多径信号的影响,DBF已经无法完成角度估计,与SS-MUSIC和AP-MUSIC算法相比,ADMM算法具有较窄主瓣及较低旁瓣,从而表明所提算法具有较高的DOA估计精度。

图2 理想反射面多径传播模型

图5 波束合成结果
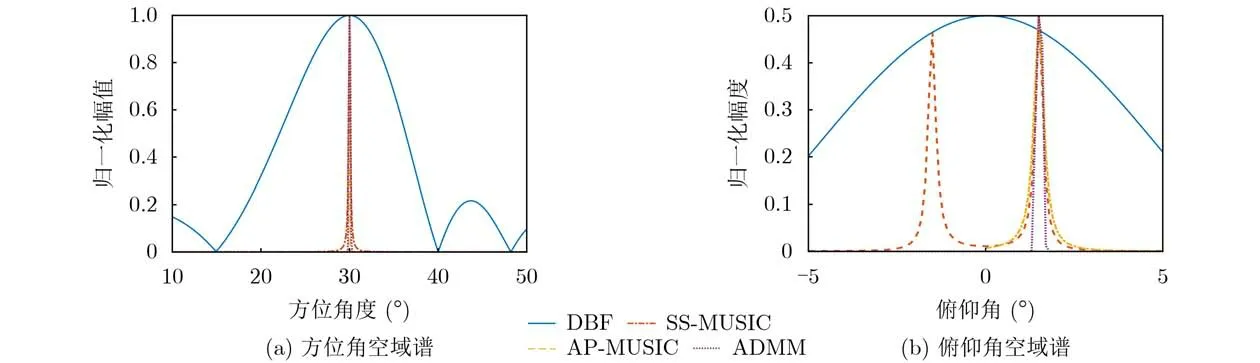
图6 目标空域谱
实验2 为了验证本文算法测角性能,对比不同信噪比条件下本文所提算法、SS-MUSIC和APMUSIC算法角度估计性能。图7为本文算法200次蒙特卡罗实验方位俯仰角估计RMSE随信噪比变换曲线,图8为单快拍3种算法俯仰角RMSE随信噪比变化曲线。从图中可以看出当信噪比较低时,本文算法与AP-MUSIC算法RMSE相差0.1°左右,信噪比较高时,两算法测角精度基本一致,可以看出两算法在测角精度上基本相同。SS-MUSIC算法测角精度与本文算法差距较大,且该算法测角精度与子阵个数有关,适用性较差。图9为20次快拍条件下,3种算法俯仰角RMSE随信噪比变化曲线,从图中可以看出20次快拍条件下,3种算法测角精度得到提升,本文算法测角精度最优,AP-MUSIC算法与本文算法测角精度相差不大,而SS-MUSIC算法测角性能较差。

图7 方位俯仰角RMSE随信噪比变化曲线

图8 单快拍俯仰角RMSE随信噪比变化曲线

图9 20次快拍俯仰角RMSE随信噪比变化曲线
为了对比算法之间的运算效率,表1给出各算法单次运行所需时间。由表1可知本文算法运算效率明显优于AP-MUSIC算法,其原因在于本文方法无需进行特征分解,且收敛速度快。SS-MUSIC方法由于不涉及迭代过程,运算速度快,由于求解过程需进行特征分解,当阵面较大时,特征分解运算时间将大幅增大,因此在保证精度要求的前提下,本文所提算法更具优势。

表1 各算法运行时间表
5 结束语
本文提出了一种适用于米波面阵雷达的快速2维角度估计方法。该算法通过行、列波束合成技术将2维DOA估计转化为两个1维DOA估计,避免了2维联合估计复杂的计算量,复杂度大大降低。使用ADMM算法进行角度估计在保证测角精度的条件下无需特征分解,不损失阵列有效孔径,算法收敛速度更快。因此,本文算法更加高效,适用范围也更加广泛。
