基于正余弦算法的文本特征选择*

文 武，万玉辉，文志云

(1.重庆邮电大学通信与信息工程学院，重庆 400065； 2.重庆邮电大学通信新技术应用研究中心，重庆 400065；3.重庆信科设计有限公司，重庆 401121)

1 引言

随着信息时代的来临，越来越多的民众通过互联网获取信息，这些网络资源大多以文本的形式存在。因此，文本自动分类技术作为处理大数据的关键技术，发挥着越来越重要的作用。随着以文本形式存在的网络数据量的增加，庞大的文本特征空间严重影响了数据分析性能。过多的噪声和冗余特征，不仅降低了训练模型的效率，更影响了分类准确性。因此，从特征空间中选出最能表达文本属性的特征，对提升文本分类性能至关重要。

在文本特征选择上，互信息MI(Mutual Information)[1]、卡方统计CHI(CHI-square statistics)[2]和信息增益IG(Information Gain)[3]等经典过滤式特征选择算法能够筛选出类别相关性较强的特征，但忽略了词与词之间的冗余性。为了获取精选特征集合，许多特征选择算法被提出。文献[4]结合皮尔逊相关系数和互信息函数，选出了类别相关性高且冗余度低的特征。文献[5]先通过多种封装式方法进行特征初选，再采用改进后的遗传算法来减小特征的数量，去除冗余的同时提高了分类精度。朱文峰等[6]通过IG提取与类别相关性较强的特征，在最大相关最小冗余mRMR(Max-Relevance and Min-Redundancy)中引入类差分度来更新特征与类别权重，去除冗余，提升了分类准确率。此外，随着群智能算法在特征选择上的应用，文献[7]结合粒子群算法和MI，采用准确率作为适应度函数，提高了分类精度。文献[8]首先从UMLS(Unified Medical Language System)中提取关键特征，再通过粒子群对提取的特征进一步优化组合，提高了对医学类文档的分类性能。文献[9]通过正余弦算法SCA(Sine Cosine Algorithm)在18个数据集上进行特征选择，准确率相比粒子群算法和遗传算法均得到了一定的提升。温廷新等[10]通过CHI进行特征初选，在果蝇优化算法中引入交叉算子和轮盘赌方法等来进行二次特征选择，保证了种群多样性，同单一的CHI方法相比用较少的特征数取得了较优的分类效果。文献[11]先通过CHI进行预选，再采用水波优化算法进行二次特征寻优，同多种传统算法相比，在5个特征维度下均提高了分类性能。

本文结合已有的研究，提出了一种二阶段寻优算法。该算法采用信息增益进行特征预选，再结合拥有全局和局部搜索能力的正余弦优化算法进行二次精选。

2 基本算法

2.1 信息增益

信息增益IG依据某特征s为整个分类系统所能提供的信息量多少来衡量该特征的重要程度，从而决定对该特征的取舍，是一种基于信息熵的评估算法。熵可以视为描述一个随机变量的不确定性的数量，熵越大，不确定性越高，那么，正确估计其值的可能性就越小。IG是在加入此特征前后文本的熵的差值，计算方法如式(1)所示：

(1)

2.2 正余弦算法

2016年，澳大利亚学者Mirjalili[12]通过总结群智能算法，提出了一种新的智能算法——正余弦算法SCA。该算法主要通过正弦和余弦函数来实现对优化问题的求解，具有原理简单、参数少和搜索机制独特等优点，获得了广泛的研究与应用。

正余弦算法在求解高维问题时，先初始化种群规模为m，搜索空间为n维，xi=(xi1,xi2,xi3,…,xin)表示第i个个体的位置，i=1,2,…,m。第i个个体按式(2)进行迭代更新:

(2)

(3)

其中，a为常数2，t为当前迭代次数，tmax为最大迭代次数。在正余弦算法中，控制参数r1是一个随着迭代次数的增加，从2慢慢减小到0的系数，用于控制局部开发与全局探索。参数r2决定了当前解向最优解远离或者接近所能达到的距离极值。r3为随机权重，是指最优解对当前解的影响程度，|r3|>1表示最优解对当前解有较强影响力，|r3|<1表示最优解对当前解影响力较弱。r4描述了随机选择正弦还是余弦进行位置更新，拟消除移动步长和方向存在的联系。当|r1·sin(r2)|>1或|r1·cos(r2)|>1时，新个体位置位于候选解和最优解之外，处于全局探索阶段；当|r1·sin(r2)|<1或|r1·cos(r2)|<1时，新个体位置位于候选解和最优解之间，处于局部开发阶段。算法通过参数的随机性，在正弦函数和余弦函数之间不断进行全局探索和局部开发来迭代更新，直至找到最佳位置。

3 基于SCA的特征选择

IG进行特征初选后会存在特征冗余问题，为进一步优化特征质量，本文对原始SCA进行改进，对特征进行二次筛选。本文在原始SCA算法的基础上，分别添加了自适应权重因子、新的适应度函数和位置更新机制来进一步优化特征子集。混合特征选择算法在本文中简称为IGISCA(Information Gain and Improved Sine Cosine Algorithm)。

3.1 个体编码

本文采用二进制编码的方式来表示特征的选择与否，每一个个体都是一个可能的最优解。首先，需要对个体位置进行离散化处理，假设有m个个体，每个个体的位置为xi=(xi1,xi2,xi3,…,xin)，由n个[0,1]的随机数组成，n表示特征的维数。这样，个体的位置由一组[0,1]的小数组成。根据一定的转化方法，将个体位置xi转化为长度为n的二进制位置x′i=(x′i1,x′i2,x′i3,…,x′in)，其中x′ij∈{0,1},j∈[1,n]。x′ij代表一个特征，值为1表示该特征被选择，值为0则表示该特征未被选择。每一个二进制位置都表示一个特征子集。个体的二进制位置x′ij可由式(4)得到:

(4)

其中，对于二进制编码，假设数据集中有6个特征{a1,a2,a3,a4,a5,a6}，随机初始化个体的位置，根据式(4)假如有个体的二进制位置为{1，0，1，1，1，0}，表示特征a1,a3,a4,a5被选取。特征a2,a6未被选取。m个个体各自遍历一次后可得到m个特征子集，根据适应度函数从中选择出最优的特征子集。

3.2 自适应权重

惯性权重[13]是群智能优化算法中重要的一项权重，描述的是上一代候选解集对当代候选解的影响程度。从式(2)可以看出，在传统的SCA中，候选解分量具有固定惯性权重1，固定惯性权重有可能会影响算法探索和开发的能力，进而影响整体的求解效果。为了避免这种情况，本文提出随着迭代次数的增加动态更新权重的公式，如式(5)所示：

(5)

其中，wmax为最大权重，wmin为最小权重，t为当前迭代次数，tmax为最大迭代次数。这样可以保证在算法初期，w的值相对较大，具有较大的搜索范围，而在后期，w的值相对较小，能够进行良好的局部搜索，快速找到全局最优。由此得到第i个个体的迭代更新如式(6)所示：

(6)

3.3 适应度函数及更新机制

适应度函数对于特征选择有重要影响，特征选择的目的是获取最优的特征子集，使分类效果得到提高。通常将分类准确率作为评价特征子集的一个重要因素；同时，用越少的特征得到更好的分类效果，是理想的特征子集。结合以上2种因素，本文采用的适应度函数如式(7)所示：

(7)

其中，p是分类准确率，nt是被选中个体的特征长度，Nt是特征的长度。α，β是2个参数，β=1-α，α是趋近于1的常数。适应度函数值越小表示结果越好。

如果只考虑适应度函数作为更新评判标准，当新一代个体适应度函数值和上一代最佳相等时，此时保留上一代最优个体，但有可能新一代个体的特征个数更少。因此，本文借鉴已有研究[14,15]，提出了2种条件下的新的位置更新机制：

(1)如果新一代个体的适应度函数值优于之前全局最优个体，则更新最优个体。

(2)如果新一代个体的适应度函数值等于之前全局最优个体，并且新一代个体选择的特征个数较少，则更新最优个体。

4 IGISCA特征选择流程

IGISCA算法通过二进制个体的位置来表达所选择的特征子集，再通过适应度函数来评价该位置的优劣。图1描述了二阶段特征选择的主要流程，在信息增益初选特征集合的基础上通过正余弦算法寻优，具体算法流程如算法1所示。

Figure 1 Flow chart of feature selection of IGISCA图1 IGISCA的特征选择流程

算法1IGISCA

输入：预处理后的特征集合Feature，种群大小m，最大迭代次数tmax，最大权重wmax，最小权重wmin。

输出：终选特征IGISCAFeature。

Step1对特征集合Feature进行IG初选，选取结果存入IGFeature中。

Step2初始化种群x，维度n，每个个体位置xi=(xi1,xi2,…,xin)，i=1,2,…,m。

Step3计算种群个体适应度值，记录当前最佳个体。

Step4更新参数r1,r2,r3,r4。

Step5若r4<0.5，采用正弦函数更新，否则采用余弦函数更新，迭代次数加1。

Step6计算新的个体适应度值，根据更新机制选出最佳个体位置。

Step7若t

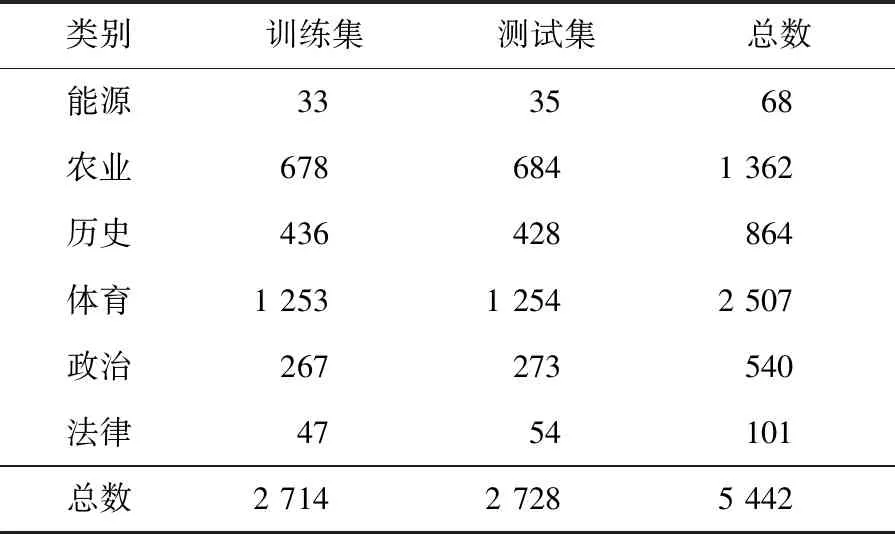
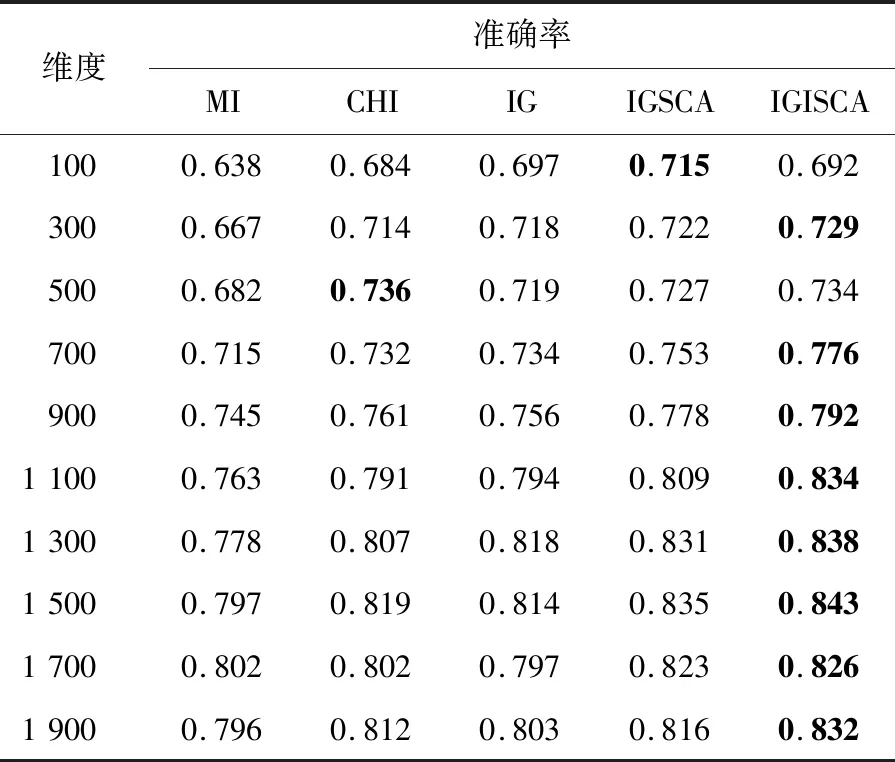
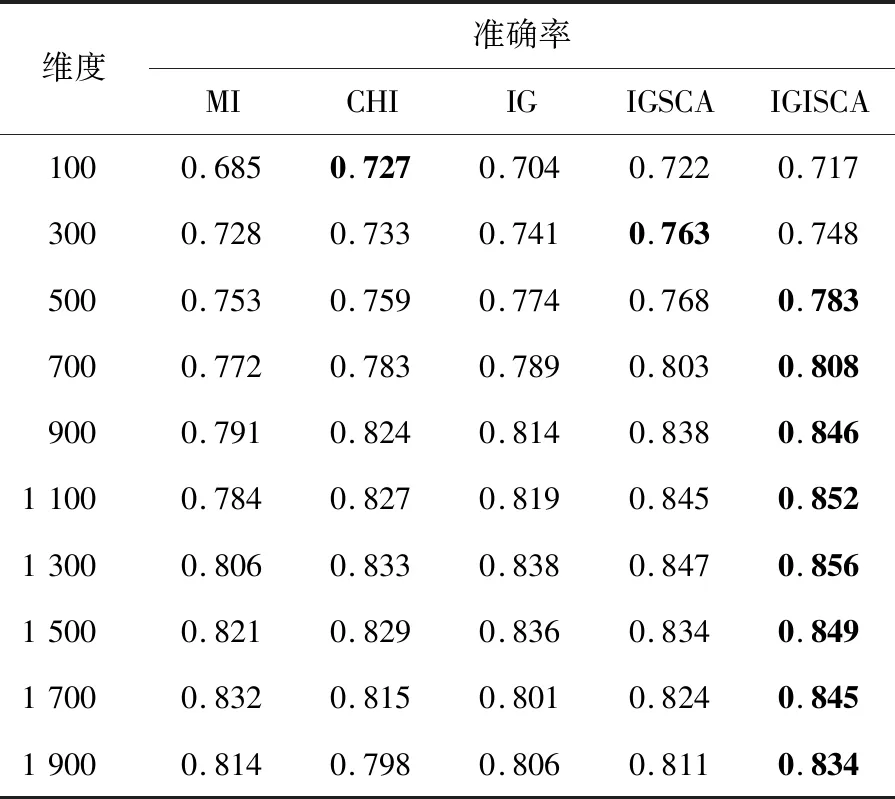
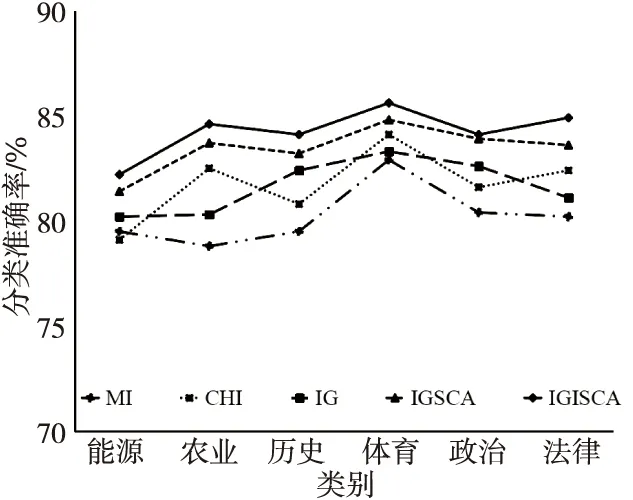
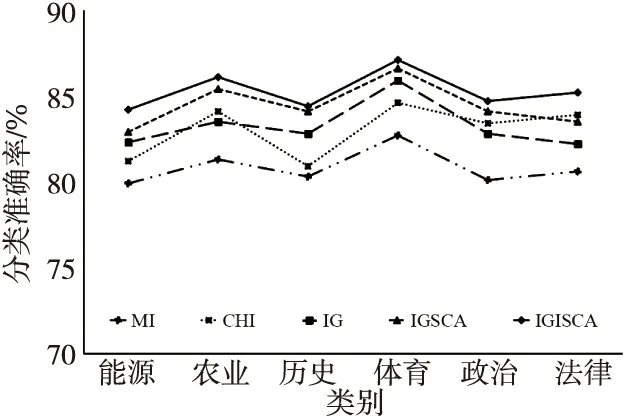
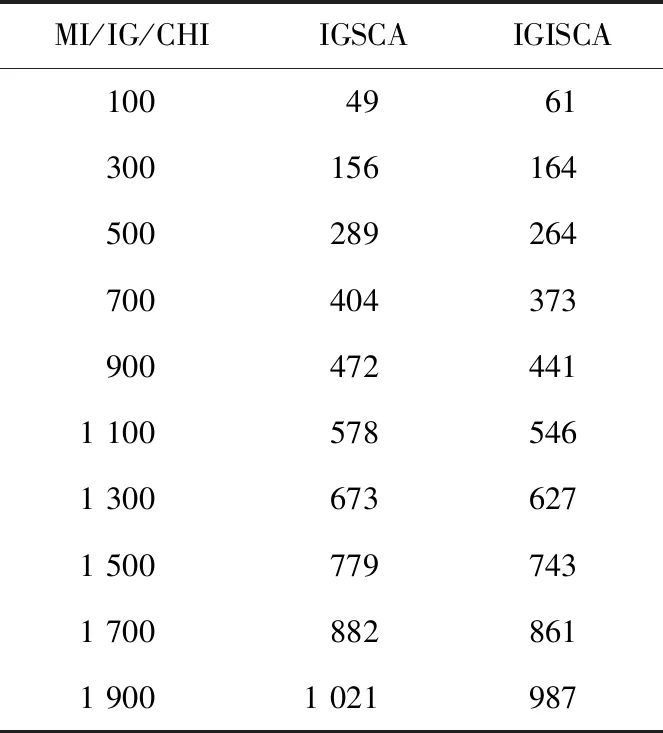
5 实验与结果分析

本次实验操作系统为Windows 10，借用Anoconda库，采用Python语言编写。为验证本文算法的有效性，实验采用MI、CHI、IG、IGSCA(Information Gain and Sine Cosine Algorithm)和IGISCA对文本集合进行特征选择，在KNN(K-Nearest Neighbor)和贝叶斯分类器下进行实验。其中，IGSCA算法是指通过文献[12]中提出的SCA算法在IG基础上进行二次特征选择，适应度函数采用分类准确率。首先使用jieba分词对数据文档进行分词，随后使用哈尔滨工业大学的停用词表对数据去停用词，通过向量空间模型进行文本表示，特征权重由TF-IDF(Term Frequency-Inverse Document Frequency)计算。评价指标为分类准确率，如式(8)所示:

(8)

5.1 实验数据与参数

实验数据选取了复旦大学数据库中的5 442篇文档，包括能源、农业、历史、体育、政治和法律6个类别，如表1所示。

Table 1 Experimental data表1 实验数据

IGSCA算法和IGISCA算法中的种群大小均设置为m=40，最大迭代次数tmax=80。IGISCA算法中最大权重wmax=0.9，最小权重wmin=0.3，适应度函数权重α=0.9。

5.2 结果与分析

为保证所有算法对比的有效性，用5种算法在100～1 900的10个维度下进行实验，在相同维度下(IGSCA和IGISCA中为IG初选维度)进行分类准确率对比，分别采用KNN和贝叶斯分类器进行分类，分类器参数保持一致。此外，为更进一步分析IGISCA算法的分类性能，统计出了各个类别下的分类准确率和二次选择后的特征个数。

(1)特征维度实验。

表2表明，在特征维度为300和700～1 900时，IGISCA的分类准确率比其它特征选择算法的高。维度为100时，IGSCA的分类准确率最高。维度为500时，CHI的分类准确率最高。整体上来看，在大部分维度下IGISCA相对于IGSCA准确率提高了0.7%～2.5%，IGISCA相对于IG分类准确率提高了约1.1%～4.2%，在大部分维度下IGISCA相对于CHI准确率提高了0.8%～4.4%，在所有维度下IGISCA相对于MI准确率提高了2.4%～7.1%。简言之，二阶段特征选择算法IGISCA在KNN分类器下能够在绝大部分特征维度下提高分类准确率。

Table 2 Feature dimension experiment under KNN表2 KNN下的特征维度实验

从表3看出，在500～1 900特征维度下，IGISCA的分类准确率优于其它特征选择算法的。维度为100时，CHI的分类准确率最高。维度为300时,IGSCA的分类准确率最高。整体上来说，在大部分维度下IGISCA相对于IGSCA准确率提高了0.5%～2.7%，在所有维度下IGISCA相对于IG准确率提高了0.7%～3.2%，在大部分维度下IGISCA相对于CHI准确率提高了1.5%～3.9%，在所有维度下IGISCA相对于MI准确率提高了2.0%～6.8%。说明了二阶段特征选择算法IGISCA在贝叶斯分类器下能够获取较优特征集合。

(2)类别实验。

由表2和表3知，在KNN和贝叶斯分类器下，IGISCA分别在IG初选为1 500维和1 300维时达到最高分类性能。为进一步验证IGISCA的可行性，单一过滤式特征选择算法在KNN分类器下选取1 500维，在贝叶斯下选取1 300维,IG初选后的特征再分别通过改进前后的SCA算法分别进行二阶段特征提取，计算出对各个类别的分类准确率。

Table 3 Feature dimension experiment under NB classifier表3 贝叶斯分类器下的特征维度实验

由图2可知，IGISCA和IGSCA 2种混合特征选择算法的分类准确率相对于其它单一特征选择算法，在所有类别文本上均有提升，表明混合特征选择算法能够在去除冗余的同时实现分类性能的一定提升。由图3可知，贝叶斯分类器下，尽管在法律类别文本上，IGSCA算法的准确率低于单一特征选择算法CHI的，但在其它类别文本上，混合特征选择算法的分类性能均高于过滤式特征选择算法的。此外，IGISCA算法在各个类别上的分类性能相对于对比算法均有不同幅度的提升，表明了本文算法的有效性。

Figure 2 Category experiment under KNN classifier图2 KNN分类器下的类别实验

Figure 3 Category experiment under NB classifier图3 贝叶斯分类器下的类别实验

(3)特征个数。

为验证本文提出的以特征个数和分类准确率加权的适应度函数和更新机制的有效性，更进一步说明IGISCA算法能够去除冗余。IG初选特征后通过SCA和ISCA分别进行寻优，统计出了2种分类器下各算法在不同初选特征维度下寻优后最终选出的特征个数，如表4和表5所示。其中，IGSCA采用分类准确率作为适应度函数。

Table 4 Number of features selected by each algorithm under KNN classifier表4 KNN分类器下各算法选择的特征个数

Table 5 Number of features selected by each algorithm under NB classifier表5 贝叶斯分类器下各算法选择的特征个数

通过表4和表5可以看到，在2种分类器下，二阶段特征选择算法相比于传统单一特征选择算法，在各个维度下实现了特征数量的大幅度约减，说明了混合特征选择算法能够在单一特征选择算法的基础上剔除冗余特征及类别相关性不强的特征。此外，同原始IGSCA算法相比，IGISCA算法筛选出的特征个数在绝大部分维度下进一步减少了，验证了改进SCA算法的有效性。

6 结束语

本文借鉴了过滤式特征选择算法和群智能算法相结合的模型进行文本特征选择，根据正余弦优化算法较强的寻优能力，提出了结合信息增益和正余弦优化算法的新的特征选择算法。该算法在信息增益的基础上，通过正余弦优化算法的全局和局部搜索寻找更能代表文本属性的特征子集。为更好地平衡早期阶段的全局搜索和后期阶段的局部寻优，在SCA算法中加入自适应惯性权重，引入了新的适应度函数和更新机制，来精确评价特征子集，实现了特征数量的消减。在KNN和贝叶斯分类器下进行实验验证，与MI、CHI、IG和IGSCA算法对比，IGISCA能够在绝大多数维度下得到更高的分类准确率，并能实现接近一半特征数量的消减，证明了本文算法的有效性。未来将对IGISCA算法继续进行优化，并尝试将正余弦算法与其它文本特征选择算法相结合，进一步检验算法的稳定性。