基于差分隐私保护的Stacking集成聚类算法研究*

李 帅，常锦才，李吕牧之，蔡昆杰

(1.华北理工大学理学院,河北 唐山 063210;2.河北省数据科学与应用重点实验室，河北 唐山 063210)

1 引言

在万物智能、万物互联的算力经济时代，对大数据的聚合与挖掘技术发展迅速。依靠数据挖掘技术获取各数据项之间的内在关联是人工智能技术的核心工作[1]。已有的数据挖掘技术包括聚类、分类、回归、关联、序列和偏差[2]。聚类[3]作为一种典型的无监督算法，将样本数据划分为若干簇，实现“簇内相近、簇外相远”的目的。与分类不同，聚类不要求数据集中含有预先定义的类别标签，无需了解数据集的背景知识，仅通过对数据的数值特征进行计算实现集合划分，分析其关联规则。由于对数据进行聚类时容易造成用户的隐私泄露，研究人员开始探索如何在聚类过程中有效保证数据安全，隐私保护数据挖掘[4]已成为近年来的热门研究方向。

目前隐私保护技术主要分为分组保护、加密保护和失真保护。分组保护是对数据集中包含用户隐私信息的特征进行删除或修改，其代表性成果有：Sweeney等[5]提出了基于准标识符处理的k-Anonymity方法，但该方法在攻击者掌握背景知识或敏感特征取值单一时易泄露隐私；Machanavajjhala等[6]提出了利用等价类替代敏感特征的l-Diversity方法，但特征值相近时可能受到相似性攻击；Li等[7]提出了t-Closeness方法，通过设置等价类和数据集中敏感属性分布距离的上限保护隐私，但数据损失较大且难以保护身份信息。加密保护通过对称加密、非对称加密和同态加密等技术对原始数据进行加密，虽然保证了传输过程中数据的安全性，但难以寻找可信第三方，且加解密过程易产生较大的算力开销。

以上隐私保护方法在解决部分隐私问题的同时未对模型做出合理假设，在攻击者掌握数据背景时仍有可能失效。失真保护通过扰乱原始数据来保障隐私安全，克服了上述方法的缺点，但如何达到数据可用性和安全性的平衡成为了难点。基于此，Dwork[8]提出了差分隐私DP(Differential Privacy)，通过严格的数学推导和定量的随机噪声实现可度量的隐私保护，与攻击者拥有的数据背景无关，迅速成为研究热点。

Blum等[9]首先将差分隐私引入K-means聚类算法，但查询函数敏感度大，且未明确隐私保护预算ε的分配方式。Dwork[10]完善了DPK-means算法中ε的分配方式。Dishabi等[11]将差分隐私应用到基于小波变换的聚类算法中，通过降低数据维度来减小噪声。Ni等[12]实现了多核密度聚类算法的隐私安全，并使用网络用户数据验证了其可行性。Zhang等[13]改进了DPK-means算法，使用轮廓系数对其性能进行评价。Sun等[14]提出了基于密度的峰值聚类，并将满足差分隐私的噪声添加到局部密度和欧氏距离矩阵中，在保护用户隐私的同时提高了聚类性能。Zhang等[15]通过改进模糊C均值算法中隐私预算的分配比例，依据聚类中心的高斯分布为隶属度矩阵添加更均衡的噪声，提高了分簇准确性。可以看出，通过改进聚类思想、优化噪声的添加机制可同时提高聚类准确性和数据安全性，然而上述研究均使用单一算法聚类，在提升差分隐私聚类的准确性时具有局限性。

为更好地平衡数据可用性与隐私性，本文提出了基于差分隐私保护的Stacking集成聚类DPC-Stacking(Differential Privacy protected Clustering of Stacking)算法。集成多种异质聚类算法，结合轮廓系数对初级聚类算法的输出进行加权，然后插入原始数据中进行学习，从而大幅提高聚类算法精度，同时针对原始数据和初级聚类算法输出分别提出了自适应的ε函数p(x)，为数据添加更符合其敏感度的Laplace噪声。实验表明,DPC-Stacking算法有效提升了差分隐私保护下对数据集聚类的准确性，减少了噪声对聚类结果的影响，优于现有差分隐私保护下单一聚类算法的聚类效果。

2 预备知识

2.1 差分隐私模型

差分隐私模型无需考虑已获取的最大背景知识，通过向数据集或迭代结果中添加定量Laplace噪声使数据失真，实现严格的隐私保护，同时最大程度保证查询函数的准确性。

定义1(ε-差分隐私) 若有算法M，数据集D和D′仅相差一条记录,算法M以数据集D和D′为输入，以M(D)和M(D′)为输出，M所有可能输出的子集S(S∈range(M))满足式(1):

Pr[M(D)∈S]≤eεPr[M(D′)∈S]

(1)

则称M满足ε-差分隐私，其中ε表示隐私保护预算，其大小与算法安全性成反比。

定义2(全局敏感度) 函数f的全局敏感度定义如式(2)所示：

(2)

差分隐私为数据集添加Laplace噪声，设有查询函数f:D→Rd，其敏感度为Δq，若M满足式(3):

M(D)=f(D)+[Lap(Δq/ε)]

(3)

则称M提供ε-差分隐私保护，其中Lap(Δq/ε)表示服从尺度参数为Δq/ε的Laplace分布的随机噪声。

定义3(组合差分隐私[16]) 已知数据集D1={s1,s2,…,spnum}包含原始数据中的列向量；D2={sc1,sc2,sc3,sc4}为初级聚类算法产生的一级聚类结果，全数据集D=D1∪D2={s1,s2,…,spnum,sc1,sc2,sc3,sc4},D1和D2的ε值不同。D的相邻数据集D′={s′1,s′2,…,s′pnum,s′c1,s′c2,s′c3,s′c4},D和D′中均包含pnum+4个列向量，相对应的列向量s和s′仅相差1个样本。clui为D中任意一列数据，clu′i为D′中对应列，若算法M在clui和clu′i上的输出Si满足Pr[M(clui)∈Si]≤eεiPr[M(clu′i)∈Si]，则M满足组合差分隐私，如式(4)所示:

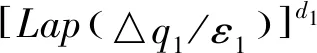
(4)

其中，ε1和ε2分别表示D1和D2对应的隐私保护预算，Lap(△qi/εi)(i=1,2)表示为Di生成的Laplace噪声。

2.2 Stacking集成学习算法

Stacking是由Woplert[17]提出的一种可用于异质学习器的串行集成学习框架，该框架采用多个初级学习器对数据集进行训练，然后利用次级学习器对初级学习器的输出进行学习，实现多个异质学习算法的融合，提升整体算法的泛化性能。

对于数据集DS={(xn,yn),n=1,2,…,N}，其中,xn为特征向量，yn为预测值，将DS划分为训练集DS1和测试集DS2。Stacking集成学习算法的流程如下所示：

步骤1选择t个初级学习器Hi(i=1,2,…,t)对训练集DS1进行训练，然后分别得到初级学习器在训练集DS1上的输出DS′1以及在测试集DS2上的输出DS′2。

步骤2使用次级学习器H′对初级学习器的输出DS′1进行训练。

步骤3使用训练好的次级学习器H′对DS′2进行预测，得到最终对测试集DS2的预测结果。

3 基于差分隐私保护的Stacking集成聚类算法

3.1 初级聚类算法的选择

在选择初级聚类算法时，算法的差异性决定着集成算法的性能，因此在选择初级聚类算法时需要综合考虑各种聚类算法间的差异，以期取得更优的聚类效果。通过对常用算法分析，本文选用以下4种聚类算法：

(1)K-means经典算法以欧氏距离作为相似度值，迭代寻找新的簇中心，预测性能较好，适用于大规模数据集。

(2)Spectral算法将数据视为无向图的邻接矩阵，通过多路划分实现聚类，但算法复杂度较高，适合小规模应用。

(3)Birch算法通过对构造出的聚类特征 CF(Clustering Feature)树进行扫描读取特征元组，分析CF树结构中的最大子树和最大距离实现聚类，时间复杂度较低。

(4)GaussianMixture算法通过计算样本满足高斯分布的概率为其分配相似度，然后对概率进行修正从而划分簇。

这4种算法的时间复杂度、可伸缩性、对噪声的敏感度以及处理较大样本集的能力均有较大差异，满足集成算法对基聚类器的要求。

3.2 基本思想

基于差分隐私保护的Stacking集成聚类(DPC-Stacking)算法将K-means、Spectral、Birch和GaussianMixture作为异质聚类算法，对原始数据集D1添加自适应的Laplace噪声得到脱敏数据集D′1，采用k折交叉验证学习D′1，合并k折预测结果，作为初级聚类算法输出。结合轮廓系数对预测集加权得到D2，为D2分配自适应噪声，得到加噪后的预测集D′2。以K-means算法为次级聚类算法，输入数据集Dtotal(Dtotal=D′1∪D′2)，产生最终聚类簇。

3.3 自适应ε函数p(x)

ε决定隐私保护程度，不同类型数据对隐私保护程度具有不同要求，因而需要添加不同大小的噪声。本文定义了DPC-Stacking算法工作过程中的自适应ε函数p(x)，验证了在集成聚类算法中分配自适应噪声的可行性。

在为原始数据集D1和初级聚类算法产生的预测集D2选择ε函数p(x)时需要注意到，原始数据集中含有较多离群点和非私密信息，且数据量较大，并无过高的隐私保护需求。而初级聚类算法产生的预测集由初级聚类算法对整个原始数据集分析得出，当聚类簇数差异较大时，易泄露用户隐私，且其风险等级依赖聚类的准确性。本文定义D1和D2上的自适应ε函数pi(x)如式(5)所示：

(5)

式(5)综合了样本规模和初级聚类算法的轮廓系数，当样本较多时不易泄露隐私，分配较大的ε。而初级聚类算法的输出中若各簇节点数相差较大，则有较高安全风险，因而分配较小的ε，添加更大的Laplace噪声。

3.4 算法流程

DPC-Stacking集成聚类算法的基本流程如下所示：

输入：数据集Da={s1,s2,…,spnum}，聚类数K，隐私预算ε，初级聚类算法φi(i=1,2,…,T)，次级聚类算法φ。

输出：经ε-差分隐私保护的聚类簇。

步骤1计算Da的隐私预算ε1=p1(x),生成Laplace噪声noise1=Lap(Δq1/ε1)；

步骤2向Da中添加噪声得到脱敏的数据集D′a,D′a=Da+noise1；

步骤3将D′a分为k个子集D′a1,D′a2,…,D′ak；

步骤4 for1≤i≤Tdo:

步骤5for1≤j≤kdo:

步骤6将D′a-D′aj输入到初级聚类算法φi,得到预测子集S′ij;

步骤7endfor

步骤8合并k个预测子集S′ik得到预测子集Si,Si=S′i1∪S′i2∪…∪S′ik;

步骤9 endfor

步骤10计算各初级聚类算法的轮廓系数λi(i=1,2,…,T)，分别对每个预测子集Si中的每个元素乘以权重系数100×λi;

步骤11合并T个预测子集Si,得到基聚类器的预测集S=S1∪S2∪…∪ST；

步骤12计算预测集S的隐私预算ε2=p2(x),生成满足ε2-差分隐私的Laplace噪声noise2=Lap(Δq2/ε2)；

步骤13向S中添加噪声得到数据集S′,S′=S+noise2；

步骤14合并数据集D′a和S得到D′，将其作为次级聚类算法φ的输入,得到最终聚类结果。

3.5 隐私性分析

由于原始数据与初级聚类算法的输出所执行的隐私预算不同，因此对于次级聚类算法所执行的聚类数据无法分析其整体隐私性。本节通过组合差分隐私间接分析DPC-Stacking算法隐私性，若所有数据块均满足ε-差分隐私保护，则算法全局满足ε-差分隐私保护。

设相邻数据集D与D′仅相差1个样本，M(D)和M(D′)分别表示DPC-Stacking算法在D与D′上的输出，S是任意一种聚类的划分结果。若M(D)和M(D′)均满足Pr[M(D)∈S]≤eεiPr[M(D′)∈S]，则DPC-Stacking算法满足ε-差分隐私保护。

证明由条件概率知

其中，σi为尺度参数，服从Laplace分布;Pr[·]为输出概率。由σi=Δqi/εi得

由f(D)-f(D′)≤Δqi得

故Pr[M(D)∈S]≤eεiPr[M(D′)∈S]，由定义3,M满足ε-差分隐私。

□

3.6 时间复杂度分析

在3.4节所述DPC-Stacking算法步骤中，步骤1和步骤2用于生成原始数据并添加噪声，其时间复杂度为O(Nd)；步骤3～步骤8中各初级聚类算法生成预测子集的时间复杂度为O(NdKI)+O(N2)+O(N2logN)+O(N2)；步骤9和步骤10对初级聚类算法的输出加权并合并至原始数据集中，其时间复杂度为O(NT)；步骤11和步骤12向预测集中添加噪声的时间复杂度为O(NT)；步骤13和步骤14使用K-means算法对扩展数据集进行聚类的时间复杂度为O(NdKI)。其中,N为样本数，d为样本维度，K为聚类个数，I为K-means算法中的迭代次数，T为初级聚类算法个数。

上述5个计算过程无嵌套关系，因而DPC-Stacking算法的总时间复杂度为5个过程中最大的时间复杂度，即O(max(N2,NT,NdKI))。由此可知，算法精度的提升虽然导致计算量略有提升，但与初级聚类算法相比，其时间复杂度仍为一个数量级，不会对算法运行时长产生较大影响。

4 实验及结果分析

4.1 实验环境及数据

实验所用计算机配置为：Intel®CoreTMi5-7200U CPU @ 2.50 GHz、8 GB内存，使用Python编程。所用数据如表1所示，DB1～DB3数据集均来自UCI数据库，DB4数据集来自DRYAD数据库。DB1为丙型肝炎血液检测数据，包含正常血液、丙型肝炎及发展至纤维化、肝硬化时期患者血液。DB2为宫颈癌行为风险数据集，包含正常受访者和宫颈癌患者的行为特征。DB3为正常受访者和肥胖症患者的饮食习惯和身体状况数据。DB4为2010年Nordsjælland 大学医院急诊科连续入院患者的常规血液检查及其死亡风险预测。

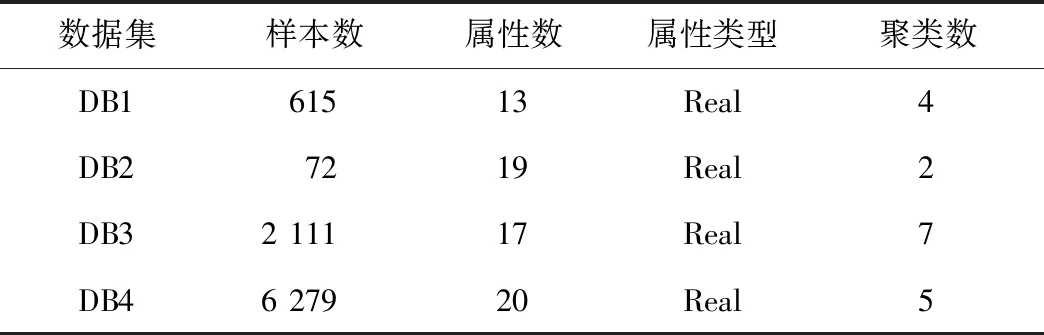
Table 1 Experimental data information表1 实验数据信息

4.2 聚类效果的评价指标

(1)Calinski-Harabasz系数。

Calinski-Harabasz(CH)系数是一种聚类的评估标准，通过簇间距离差与簇内距离差之间迹的比值，判断聚类结果集中簇内的密合程度以及各簇间的分离程度。CH系数的计算如式(6)所示：

(6)

其中，tr(·)表示矩阵的迹，Bk表示各个簇的协方差矩阵，Wk表示簇内的协方差矩阵，n表示样本个数，k表示聚类个数，CH(k)∈[-1,1]。

CH系数的值越大，代表聚类效果越好，各个簇间距离更远且簇内元素在空间中分布越紧密。

(2)轮廓系数。

轮廓系数(Silhouette Coefficient)综合考虑了内聚度和分离度，通过计算簇内和簇间的不相似度，给出聚类效果的评价。样本spl的轮廓系数定义如式(7)所示：

(7)

其中，a(spl)表示数据集的簇内不相似度，即样本spl到该簇内异于该点样本的平均距离；b(spl)为簇间不相似度，即样本spl到其他簇内样本点的平均距离。

综上，数据集的轮廓系数定义如式(8)所示：

(8)

其中，Nspl为样本个数，S∈[-1,1]。

4.3 实验结果及分析

实验对DB1～DB4进行预处理，将类别属性转换为实数，剔除含有缺失值的样本。分别对K-means、Birch、Spectral和GaussianMixture 4种初级聚类算法进行测试，然后对C-Stacking (无噪声的DPC-Stacking)算法进行测试，对比基于Stacking思想的集成聚类算法的CH系数和轮廓系数，结果如图1所示。

由图1可知，与单一聚类算法相比,C- Stacking算法经聚类计算产生的CH系数提升了43%～406%，轮廓系数提升了26.7%～83.9%。实验的数据来源于不同领域，且样本数和特征数有较大差别，但聚类性能均得到显著增强，表明DPC-Stacking算法具有较高的可用性与鲁棒性。因此可知，基于Stacking思想的集成聚类算法远优于单一聚类算法。

然后，分别令ε=0.05,0.1,0.2,0.5,1,5,10，测试DPC-Stacking算法在不同隐私预算ε下对数据集DB1～DB4的聚类效果。考虑到算法所添加的Laplace噪声具有随机性，实验结果可能存在差异，对不同ε的DPC-Stacking算法运行20次，取CH系数和轮廓系数的平均值作为结果，其对比图如图2所示。

由图2可知，随着ε的增大，为数据集分配的Laplace噪声变小，数据的可用性得到提高，因而聚类结果的准确性也不断提高。当ε<0.5时噪声过大，加噪后数据集的空间特征难以准确体现样本的实际特征，聚类结果较差。当ε≥0.5时，算法可以提供足够的隐私保护，聚类的准确性提升较大，实现了数据安全性与可用性的平衡。因此，将差分隐私保护用于DPC-Stacking算法实现安全高效的聚类是可行的。

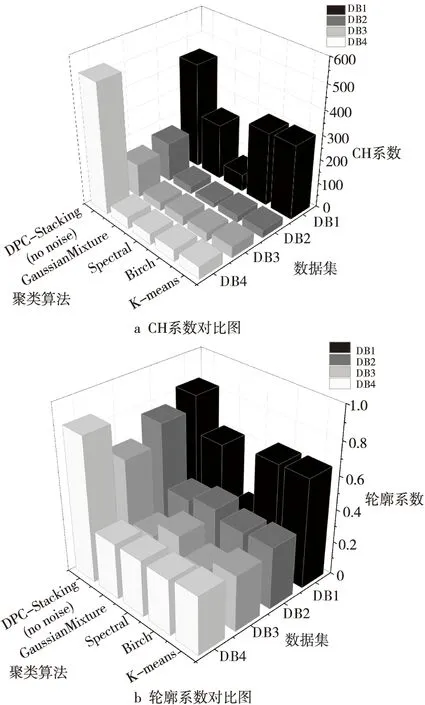
Figure 1 Comparison of performance between single clustering algorithm and DPC-Stacking(no noise) algorithm图1 单一聚类算法与无噪声DPC-Stacking算法性能对比

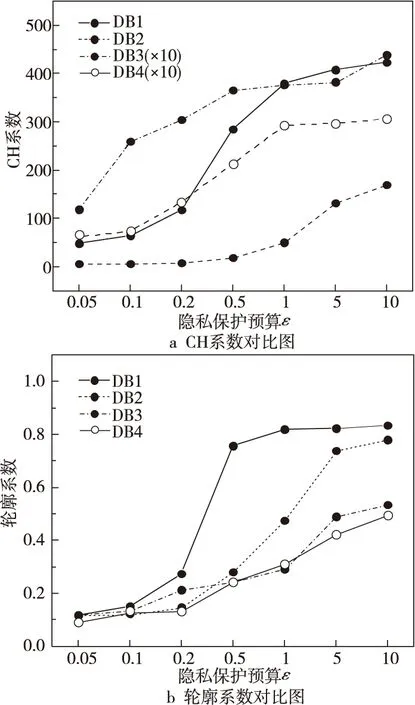
Figure 2 DPC-Stacking算法在不同ε下的聚类性能图2 Clustering performance of DPC-Stacking algorithm with different ε values

为验证3.3节提出的自适应ε函数p(x)，分别使用4种初级聚类算法对DB1～DB4进行聚类，计算原始数据集D1和初级聚类算法产生的预测集D2的ε函数p1(x)和p2(x)的值，其具体值如表2所示。将其分别代入DPC-Stacking算法，算法运行结果与图2中近似的传统ε的对比结果如图3所示。

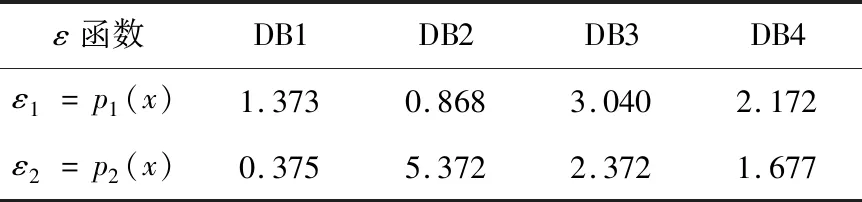
Table 2 ε function value of each dataset表2 各数据集的ε函数p(x)值

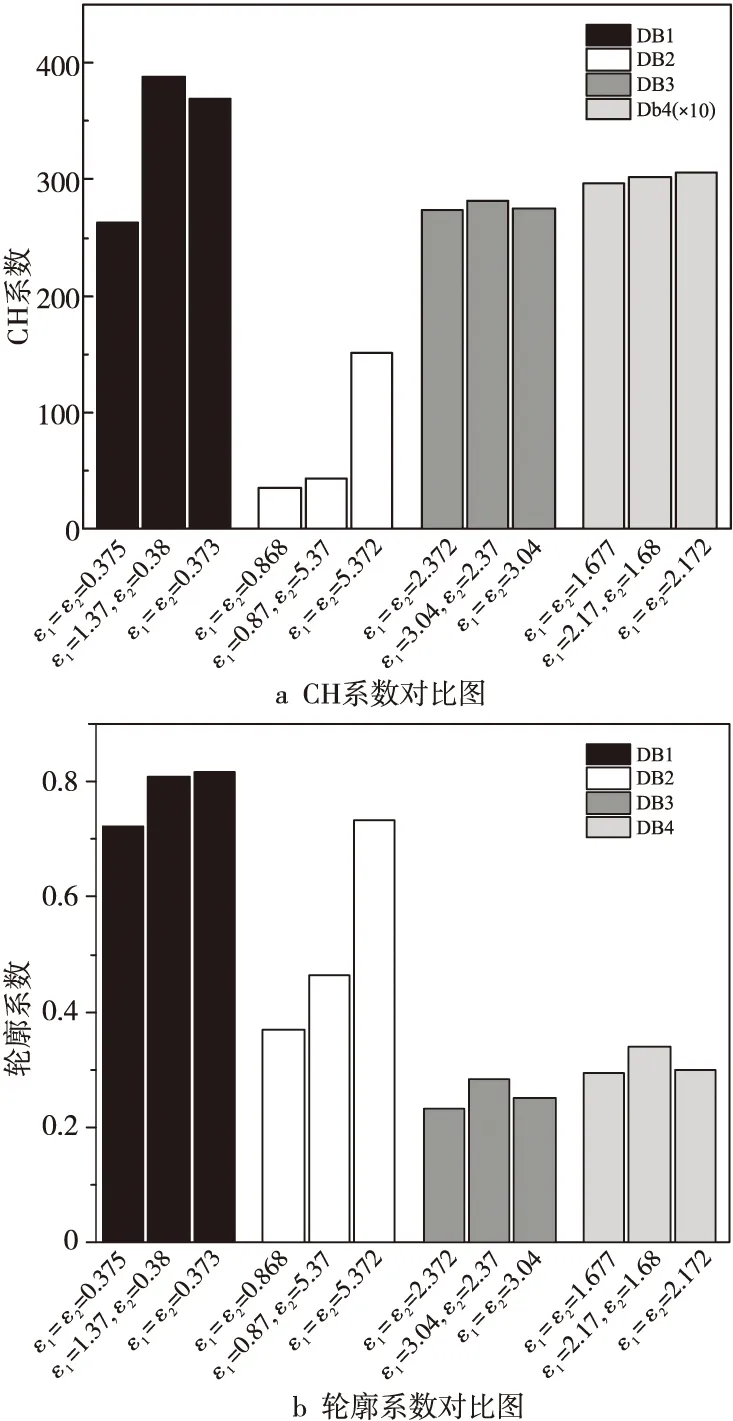
Figure 3 Comparison of adaptive ε and traditional ε clustering图3 自适应ε与传统ε聚类对比图

由图3可知，其他条件不变时，原始数据中添加的噪声对聚类算法性能的影响大于对初级聚类算法的聚类结果所产生的影响。同时，采用自适应的ε函数p(x)确定隐私预算，其生成的噪声更适合数据集的结构特点，在添加相近噪声时可产生更优的聚类效果，实现同级别的隐私保护，在满足ε-差分隐私保护的基础上仍可提升模型聚类性能，保证了数据可用性。因此，本文提出的自适应ε函数p(x)相对于传统的无差别ε具有一定的优越性。

5 结束语

数据挖掘中的隐私保护近年来备受关注，传统聚类仅采用单一算法进行分析，此时引入差分隐私对算法性能影响较大，难以保证数据隐私性与可用性的平衡。本文提出了一种基于差分隐私保护的DPC-Stacking集成聚类算法。通过改进Stacking集成学习算法，并将其与聚类算法相结合，实现了高精度的Stacking聚类算法。考虑到聚类算法在实践中易产生的隐私泄露问题，将差分隐私引入Stacking聚类算法，并提出适合该算法特性的自适应ε函数p(x)，为初级聚类算法在不同阶段的输入添加更合适的噪声，在保证数据可用性的基础上实现了可度量的隐私保护，大幅提高了聚类的准确性与安全性，为差分隐私在集成聚类中的应用开拓了新思路。