六轴宽轨机车液压减振器卸荷参数的选取
2022-08-19李建伟史青录李幸人
章 新,李建伟,史青录,李幸人,王 宇
(1.太原科技大学 机械工程学院,太原 030024;2.中车大同电力机车有限公司技术中心,山西 大同 037038)
我国机车产品已经基本覆盖“一带一路”沿线国家,其中主要出口国包括前苏联加盟国及蒙古,但其采用1 520 mm 宽轨,需要针对其轨距进行改造研究[1-3]。目前对宽轨机车的研究,主要集中在转向架系统设计及动力学分析、安全性实验等方面[4-9],但对液压减振器阻尼参数的研究较少,特别是卸荷参数选取研究更为少见。
在准轨机车液压减振器的卸荷特性研究方面,秦震等[10]研究了抗蛇行减振器和二系横向减振器在固定卸荷速度值条件下卸荷阻尼力的变化对高速动车组临界速度和轮轨磨耗的影响。罗赟等[11]研究了3 种卸荷速度条件下2B0动力车的动力学性能对于卸荷阻尼力改变的敏感程度。戴焕云[12]发现铁道车辆减振器两端相对速度符合正态分布,并以衰减95%的低频振动为目标,将减振器两端相对速度的2倍均方差选取为卸荷速度,再与优化阻尼系数相乘得到卸荷阻尼力。这些研究或仅分析了卸荷特性对高速动车组的动力学性能影响,或并未验证所选取的卸荷参数对机车动力学性能的影响。
对于减振器双向比研究,现阶段主要集中在汽车领域,如Rajalingham等[13]对比分析了汽车悬架减振器阻尼对称和非对称对振动响应的影响;Silveira等[14-15]进一步研究了汽车悬架减振器非对称阻尼的变化对车辆的减振性能影响;赵雷雷等[16]对座椅减振器双向比对人-椅系统冲击动力学行为的影响进行了研究,目前对铁道车辆减振器双向比的公开研究甚少。
本文针对出口白俄罗斯的某型25 t 轴重、六轴宽轨电力机车,先进行一系垂向减振器双向比研究,然后以平稳性和衰减低频振动的可能性为目标,进行减振器复原行程卸荷参数的选取研究,再和其他卸荷参数进行不同车速下的动力学性能对比分析和验证。
1 六轴宽轨机车模型
1.1 动力学建模
该出口型六轴宽轨机车由车体、构架、轮对3大部分构成。其中一系悬挂装置由双轴箱拉杆、高圆螺旋弹簧及垂向液压减振器组成,二系悬挂采用方形橡胶堆支撑。前、后转向架结构相同,关于车体中心对称布置。
机车模型拓扑图如图1所示,根据其拓扑结构建立机车SIMPACK动力学模型,以求最大程度反映真实的机车构造。所建立六轴宽轨电力机车动力学模型如图2所示,共计90 个自由度。其中假定驱动电机(悬挂方式为轴悬式)、齿轮变速箱等这些动力源在机车行驶过程中不产生振动,将其与构架、轮对、牵引杆等共同考虑为具有质量属性的刚体[17]。

图1 机车模型拓扑图
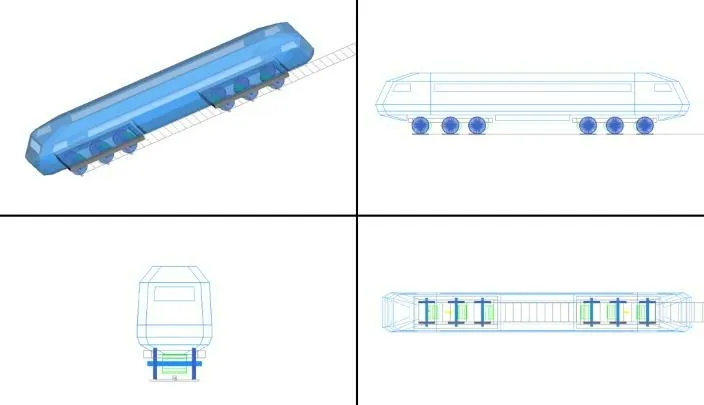
图2 六轴机车动力学模型
1.2 减振器卸荷特性
机车的一系垂向减振器卸荷特性曲线如图3所示,D点和E分别为压缩和复原行程的卸荷点。当减振器两端相对速度较高,油液压力增大,减振器接近刚性,但由于卸荷点的存在,可以有效阻止高频冲击振动的直接传递。另外,卸荷点所对应参数包括卸荷速度和卸荷阻尼力;一般将相同速度下复原阻尼力与压缩阻尼力的比值称为减振器的双向比,用β表示。
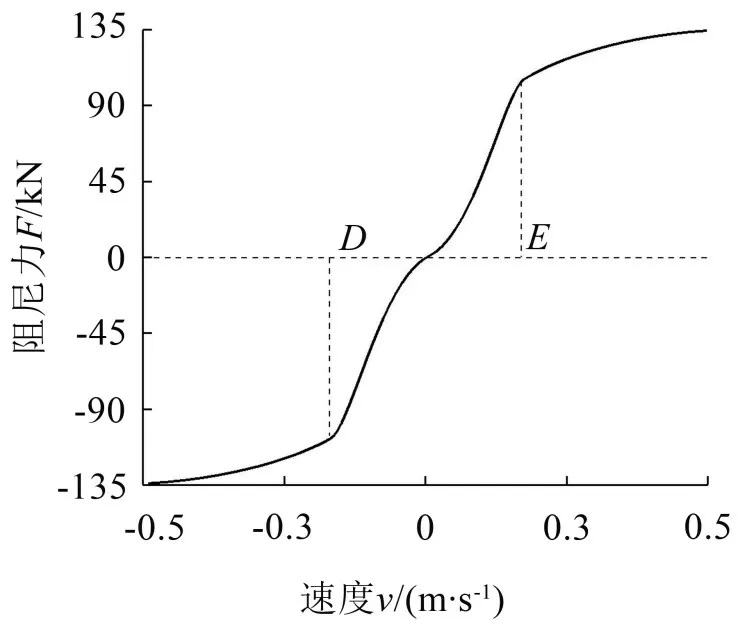
图3 减振器卸荷特性曲线
2 卸荷参数的选取方法
平稳性是衡量机车动力学性能的一项重要技术指标,其对于机车的乘坐舒适性具有十分重要的意义[18-19]。另外,若减振器卸荷阀卸荷速度选取过小,则减振器等效线性阻尼系数变小,导致其衰减振动的能力变弱;反之若过大,即卸荷阀不能及时参与工作,减振器近似刚性,冲击振动将直接通过减振器,不再能够得到有效衰减。故减振器卸荷速度和有效衰减振动的可能性密切相关[20]。
因此本文中一系垂向减振器卸荷参数的选取方法为:首先确定减振器双向比,得到复原和压缩行程的卸荷参数之间关系,然后以平稳性为目标,结合减振器两端相对速度分布范围,对复原行程卸荷参数进行选取。
机车的平稳性在本文中使用Sperling 指标法度量,其中单一频率下的Sperling指标由式(1)表示[21]:
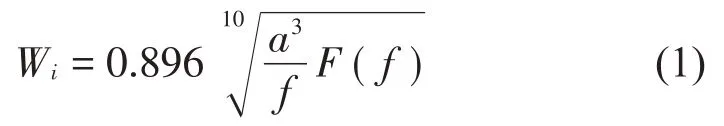
式中:Wi为单一频率的Sperling 指标;a为振动加速度幅值;f为振动频率;F(f)为频率修正系数。
实际机车的振动为随机振动,需要将测得的加速度通过40 Hz 低通滤波后按频率分组,计算出各个频段的平稳性指数Wi,通过加权获得全频带范围内的平稳性指标,总的平稳性指数按式(2)计算。
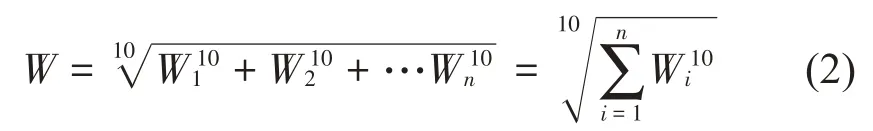
铁道车辆减振器两端相对速度总体以95 %的置信度服从正态分布。在机车以最大运行速度120 km/h直线运行工况下,计算得到一系垂向减振器两端相对速度时域响应及其概率密度分布曲线如图4和图5所示。再选用正态概率密度函数作为待检验函数,其相对速度的检验统计量为4.01,小于在显著性水平α为0.05 时的是否拒绝零假设临界值5.99。从而证明该减振器两端相对速度总体以95%的置信度服从正态分布。
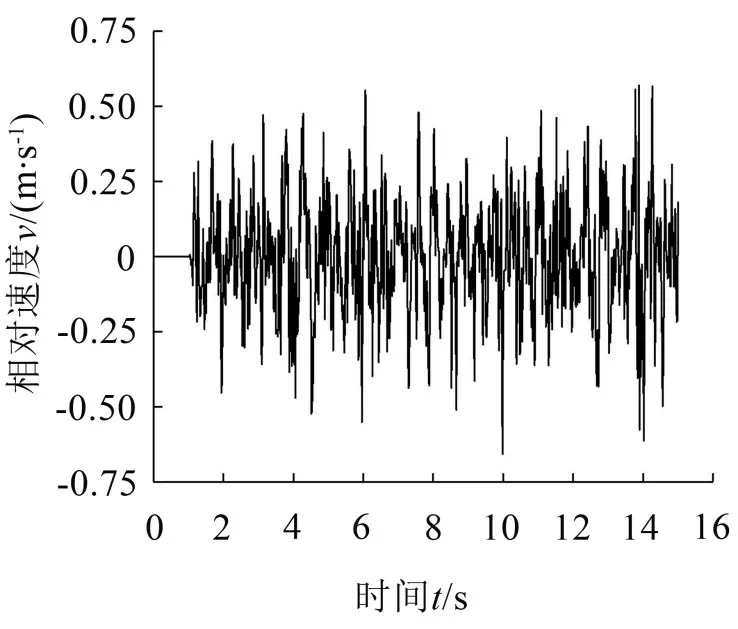
图4 减振器两端相对速度
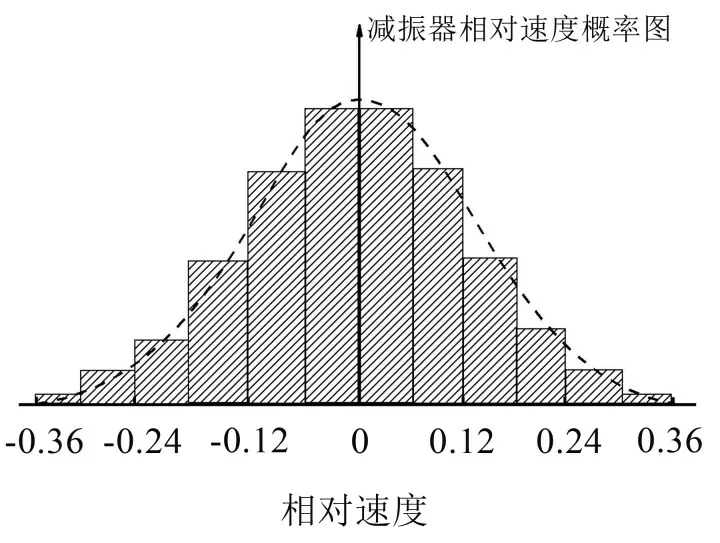
图5 相对速度概率密度
由图5可得,减振器相对速度均值μ为0,方差σ为0.12,正态分布值落在(μ-σ,μ+σ)范围内的可能性是68%,落在(μ-3σ,μ+3σ)范围内的可能性是99 %,即减振器两端相对速度落在0.12 m/s~0.36 m/s 的可能性为68%~99%,因此一系垂向减振器卸荷速度选取范围确定为0.12 m/s~0.36 m/s,将以其更有效地对此范围内的振动进行衰减。
3 减振器卸荷参数的选取
3.1 减振器双向比的确定
以AAR5 级轨道谱进行随机激励,对一系垂向减振器双向比分别为β=1/3、β=1/2、β=1、β=2 及β=3的5种阻尼模型进行仿真分析。以前司机室座椅位置为评价点,Sperling指标变化如图6所示。
由图6可见,在不同车速下双向比β=1 时的Sperling指标均明显低于β≠1的另外4种情况。故双向比为1对机车垂向平稳性的改善最有利。
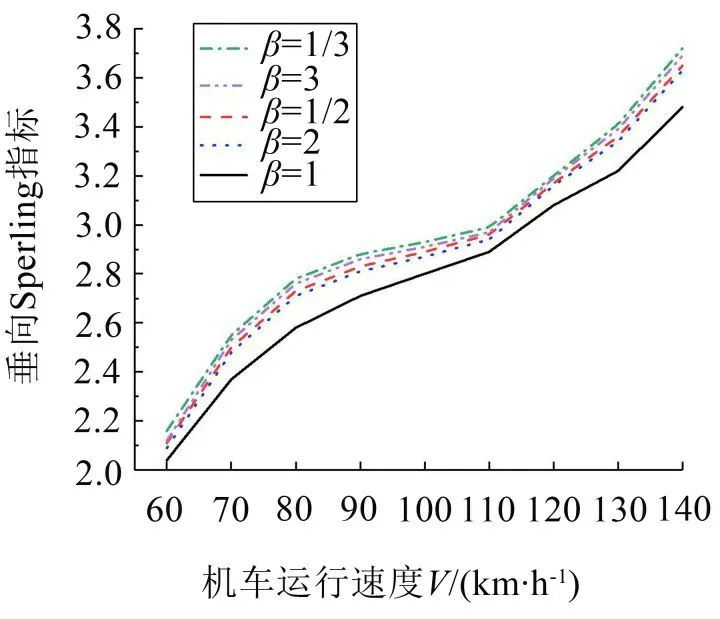
图6 一系减振器双向比对Sperling指标影响
根据白俄罗斯标准ГOCTP55364-2012 要求,一系悬挂装置垂向动荷系数的最大限值应不超过0.35,二系悬挂装置垂向动荷系数的最大限值应不超过0.25,计算公式如下:

式中:δ为垂向动荷系数;PD为作用在弹簧悬挂装置上部的垂向动态力;PCT为在弹簧悬挂装置上部的机车簧承重量产生的垂向静态力。
减振器双向比β分别为1/3、1、3这3种情况下前转向架导向轮对一、二系悬挂装置垂向动荷系数计算结果如图7所示。可见在计算速度范围内一、二系悬挂垂向动荷系数均小于最大限值0.35,满足安全行驶要求;在车速小于90 km/h条件下,β=1时一、二系悬挂垂向动荷系数要低于β≠1 时的两种情况;但在车速大于是100 km/h条件下,β=1时一、二系悬挂垂向动荷系数不再是最小。
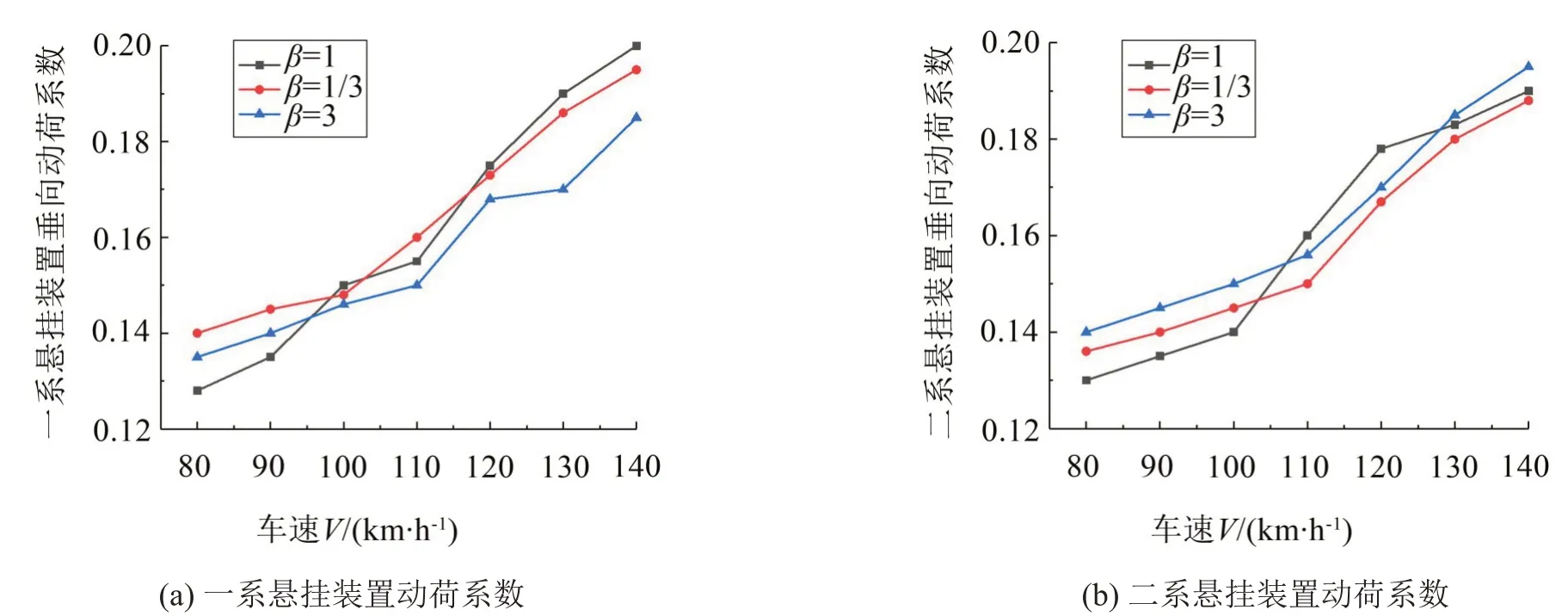
图7 不同双向比下的垂向动荷系数与车速关系
图8分别给出了3 种双向比条件下前转向架导向轮对在不同车速时的脱轨系数和以最大运行速度120 km/h行驶时各轮对的脱轨系数。可见β=1时机车脱轨系数均明显小于β≠1时的两种情况。
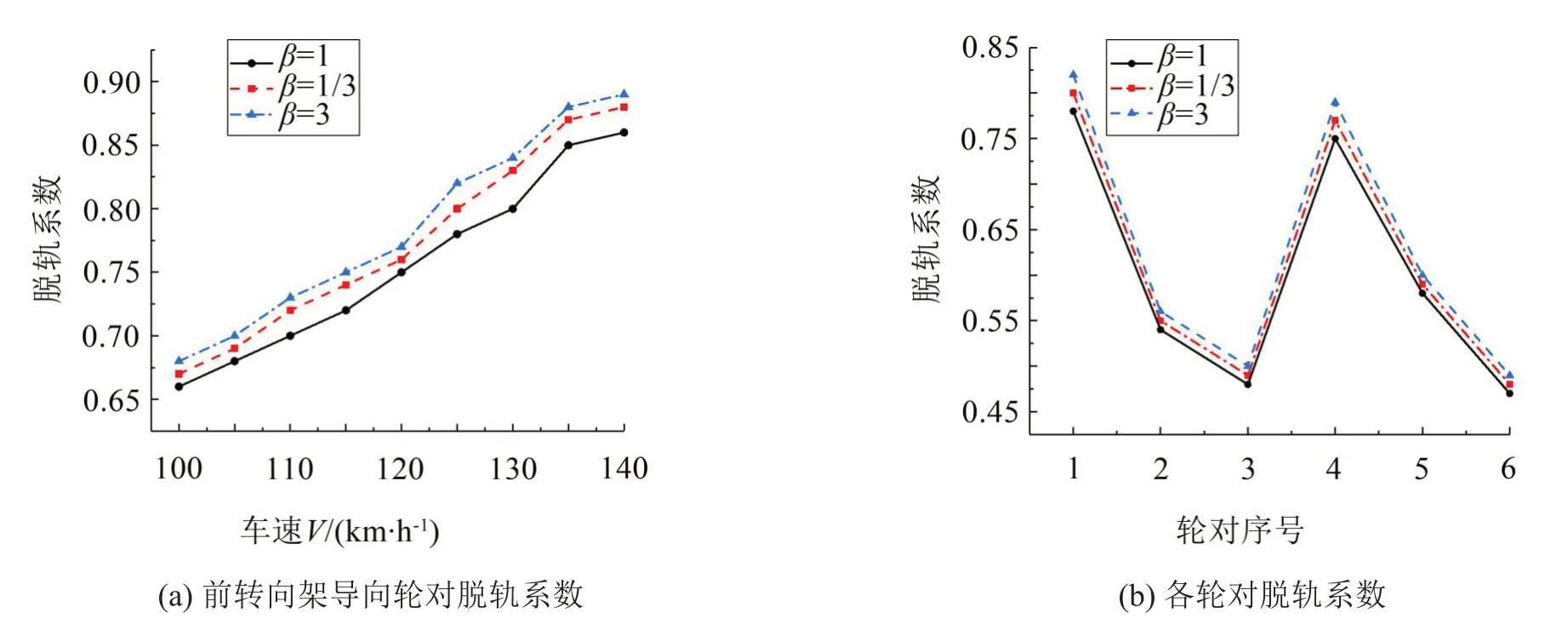
图8 不同双向比时的脱轨系数
因此文中经综合考虑确定减振器双向比β=1,此时机车动力学综合性能最好,选取压缩行程卸荷参数与复原行程相同。
3.2 复原行程卸荷参数选取
在该机车以最高运行车速120 km/h直线行驶工况下,计算得到司机室的垂向Sperling指标如图9所示。可见,卸荷速度vd、卸荷阻尼力Fd与垂向Sperling 指标三者关系呈近似碗状曲面,卸荷参数存在最优值使垂向Sperling 指标最小;在每个确定的卸荷速度下都存在最佳卸荷阻尼力。
根据图9,得到最优卸荷参数为vd=0.20 m/s、Fd=120 kN时,司机室垂向Sperling指标为2.82。
4 不同卸荷参数下动力学性能对比
为验证上述选取的卸荷参数对机车动力学性能的改善程度,将另外3种方案与其进行对比分析,其方案如表1所示。其中方案1中采用原始参数,方案2中采用上述选取改进参数,方案3中采用根据文献[14]选取方法所确定的卸荷参数,方案4 中选取卸荷速度为0.35 m/s,再由图9得到对应的最优卸荷阻尼力。
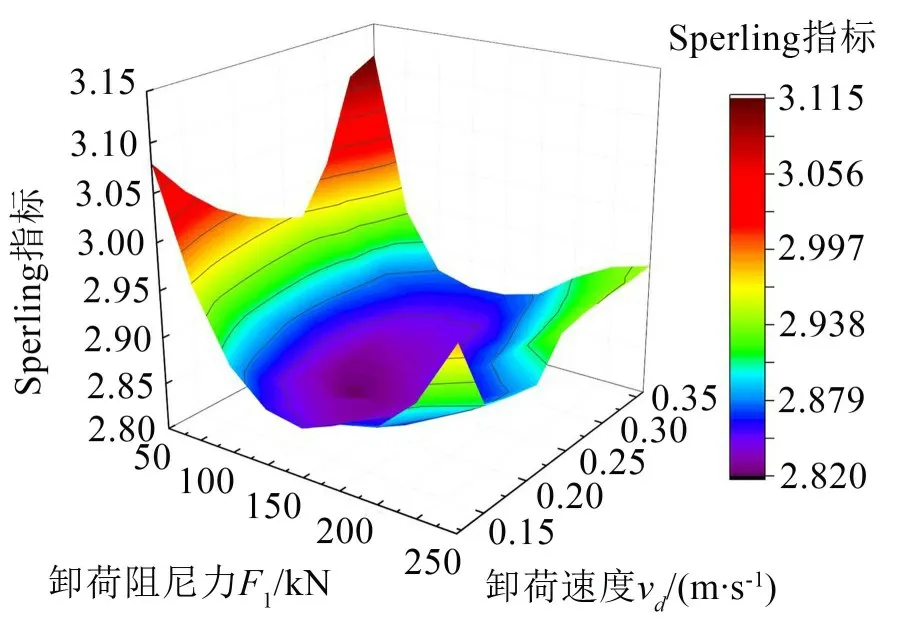
图9 卸荷参数与Sperling指标关系

表1 4种卸荷方案
4.1 Sperling指标
以AAR5 级轨道谱进行随机激励,通过仿真计算车速为70 km/h 至120 km/h 时前司机室座椅位置垂向Sperling 指标,如图10所示。可见在不同车速下,4 组方案虽均满足平稳性要求,但采取方案2 中的卸荷参数时,其Sperling 指标明显小于另外3 组方案。

图10 不同车速的Sperling指标
4.2 悬挂装置动荷系数
前转向架导向轮对一、二系悬挂装置垂向动荷系数计算结果如图11所示,可见在计算速度范围内的一、二系垂向动荷系数均小于最大限值,满足安全行驶要求。但方案2 垂向动荷系数明显低于另外3种方案。其中方案1和方案4指标明显偏大,这是由于方案1 中减振器卸荷速度过低,没能够将低频振动充分衰减;而方案4中卸荷速度过大,使得阻尼力过大,减振器接近刚性,高频冲击振动直接传递至车体。因此卸荷速度过大和过小都将导致机车一、二系的垂向动荷系数偏大。
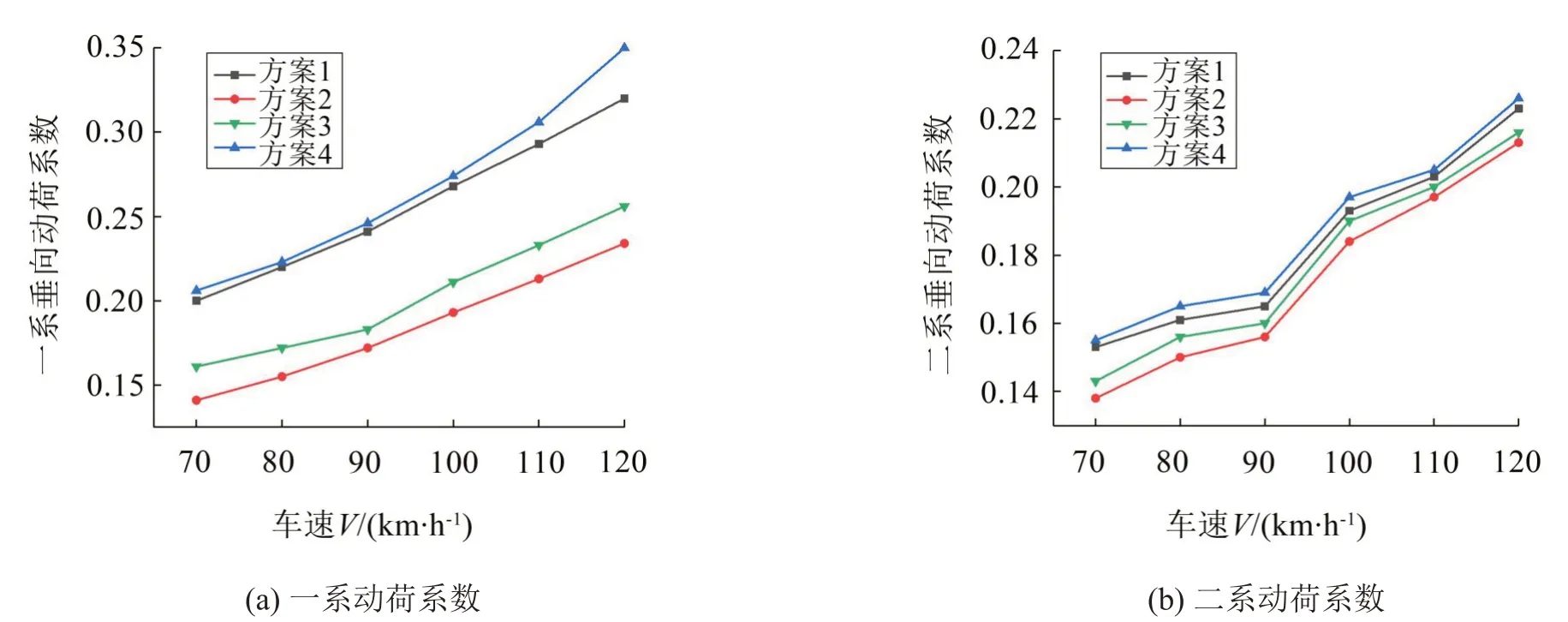
图11 悬挂装置动荷系数对比分析
4.3 曲线通过性
在AAR5 级随机激励条件下,对机车进行曲线工况下的仿真分析。曲线线路由100 m 直线段、60 m 缓和曲线段、半径R=600 m 的曲线段、60 m 缓和曲线段及100 m 直线段组成,曲线名义超高为120 mm。机车脱轨系数参照文献[22]计算及评定。
图12给出了在不同车速时前转向架导向轮对的脱轨系数、120 km/h 时各轮对脱轨系数和不同车速下的轮重减载率。可见虽然在最大车速下他们都小于0.9,4 种方案均满足合格标准[22],但方案2 机车脱轨系数和轮重减载率明显小于另外3种方案。
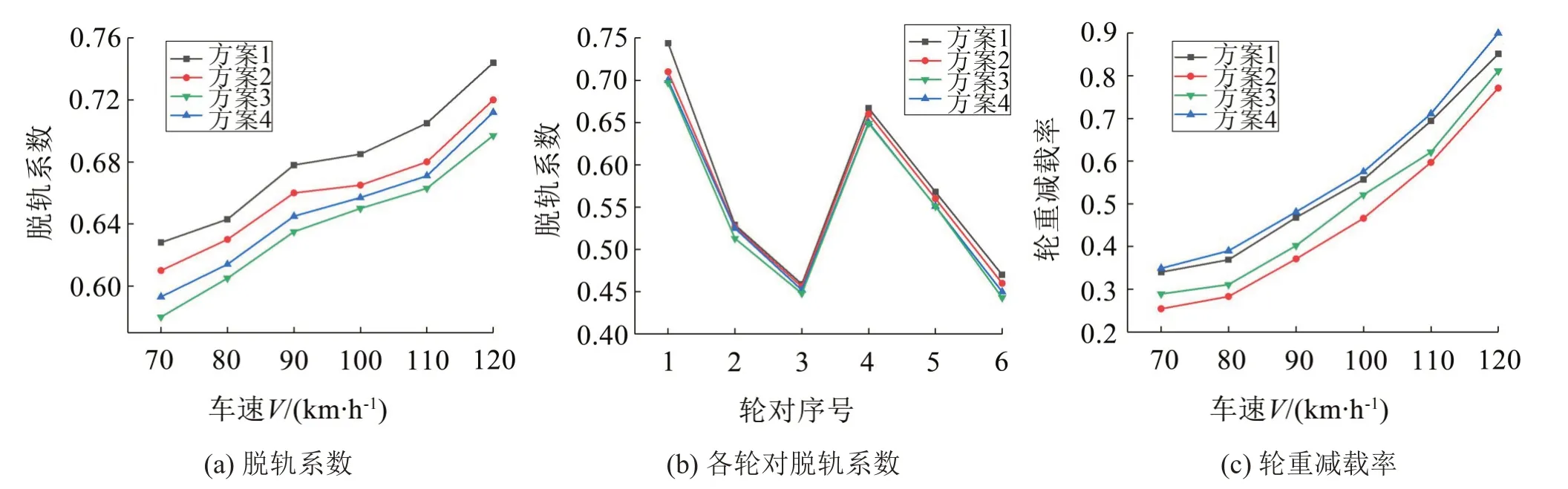
图12 曲线通过性对比分析
5 结语
本文建立含有卸荷特性减振器的六轴宽轨电力机车模型,先进行了一系垂向减振器双向比的选取,然后以平稳性为目标对减振器单侧行程卸荷参数的选取进行了研究和对比验证,得到如下结论:
(1)减振器双向比为1时,机车动力学综合性能最优,故将压缩行程与拉伸行程的卸荷参数选取为同样数值。
(2)计算表明在机车以最高车速直线行驶工况下存在减振器最优卸荷参数,其能够使机车垂向Sperling指标达到较优水平。
(3)通过与其他卸荷参数选取方案对比分析,验证了采用所选取的卸荷参数时,在Sperling 指标、悬挂装置动荷系数、脱轨系数及轮重减载率方面,机车的动力学综合性能相比于其他方案是最好的。
本文可为该型机车和其他铁道车辆减振器卸荷参数的选取提供理论依据和方法。
