城市轨道交通受电弓参数敏度分析及优化设计

祁文延，王江文，张士宇，黄 仲，卢 静，梅桂明

（1.西南交通大学 牵引动力国家重点实验室，成都 610031；2.中车长春轨道客车股份有限公司，长春 130062）

在城市轨道交通系统中，受电弓与接触网通过滑动接触完成取流为列车的运行提供电能，因此，弓网系统良好的受流对于列车运行的安全性和可靠性至关重要。2020年初，我国地铁线路总里程已达到了6 600公里，采用刚性接触网布置的线路占据了总里程的1/4，且由于刚性接触网线路具有低隧道空间、无张力、散热好、易于安装检修等特点还会在未来大幅度增加[1]。然而近年来，我国地铁线路频繁暴露出受电弓滑板与接触线严重磨损的问题，这不仅会增加列车的运营成本，也意味着受流质量的下降。因此，如何获取更好的受流质量成为弓网系统研究的重要方向。

在列车的实际运行过程中，弓网系统的受流质量往往受机械、力学、材料和电气等多方面的影响，其中动力学性能是弓网系统受流的技术基础，换句话说，弓网系统的动力学性能对于受流质量的好坏起着决定性的作用[2]。在动力学仿真分析或线路实测分析中，往往采用接触力标准差σ和平均值Fm评价受流质量的优劣[3－5]。σ代表接触力的波动程度，σ越小，接触力波动程度越小，受流质量越好。Fm代表受电弓滑板与接触线的作用力平均水平，良好的弓网受流质量体现在满足Fm的前提下使σ尽可能小，这也是弓网动力学参数优化设计的主要目标[6]。

受电弓与接触网参数是影响弓网系统动力学性能的重要元素之一，国内外学者对改变受电弓或接触网参数对于受流质量的影响做了一定研究。Lee等[7]采用SAMCEF有限元软件建立了弓网系统的仿真模型，采用优化方法对受电弓的参数进行优化，以分析受电弓参数的敏感性。Park 等[8]考虑柔性接触网跨距内的弹性变化，采用解析法分析受电弓质量、阻尼、刚度等对弓网系统耦合性能的影响。姜静等[9]综合考虑了受电弓与接触网互相影响，得到当受电弓幅频特性曲线的转折频率与受电弓通过吊弦频率相等时，可有效减小接触力标准差，改善受流质量的结论。吴孟臻等[6]通过对干线铁路DSA380 型高速受电弓的参数敏度分析得知：弓头等效参数敏度评级最高，下框架等效阻尼次之，下框架等效质量和上框架等效阻尼第三。

以上弓网参数对受流质量影响的研究大多是基于柔性接触网，而刚性接触网不仅刚度大、无张力且所用受电弓与干线铁路高速受电弓存在很大的区别，因此有必要对刚性接触网对应受电弓的参数敏度进行分析及优化设计。本文首先建立弓网耦合动力学模型，通过线路实测数据验证了模型的准确性；接着基于接触力随机统计特征作为优化目标函数，对CED125D 型地铁受电弓的三质量块参数进行了敏度分析并评级；最后实现了弓头双等效参数的优化设计，且其弓网匹配关系结果优于单参数设计，进一步给出优化建议：同时减小弓头质量及刚度、减小弓头质量同时增大弓头阻尼、减小弓头刚度同时增大弓头阻尼，可有效降低接触力标准差，提高受流质量。

1 城市轨道交通弓网系统动力学模型

1.1 刚性接触网模型

刚性接触网通常是通过钻孔安装在地下隧道结构顶部，并根据隧道的结构形式以及净空高度的不同采用不同的安装方式，其悬挂机构可根据静力学平衡条件以及动能和势能定理将其等效为弹簧质量系统，π型结构与接触线可一起等效为梁单元，如图1所示，其中的meq和keq分别为悬挂机构的等效质量和等效刚度。得到刚性接触网振动微分方程为[10]：

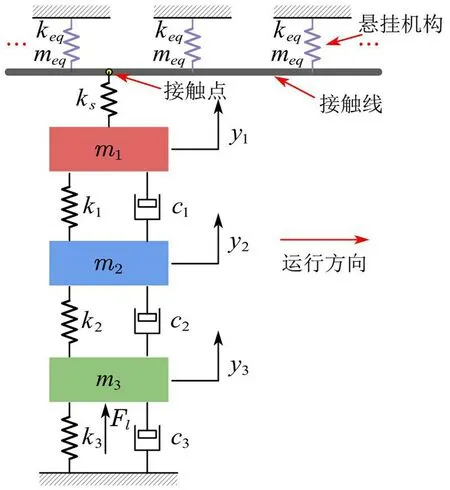
图1 城市轨道交通弓网系统耦合模型

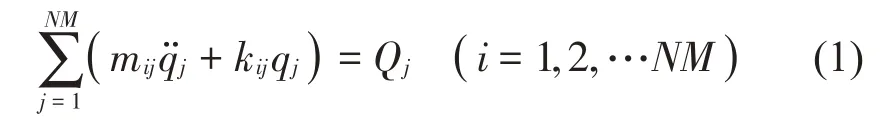
式中：mij、kij分别为模态质量和模态刚度；Qi为广义力；qj为广义坐标；NM为模态截断阶数。

1.2 受电弓模型

受电弓通常是安装在列车顶部并沿着接触线滑动的集电设备。在受电弓参数优化设计研究中，三质量块归算质量模型因其具有计算效率高且参数易获取等众多优势被广泛采用。因此，本文采用三质量块归算质量模型，建立的受电弓动力学方程如下[11]：

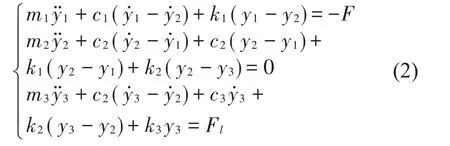
式中：m1、m2、m3分别为受电弓弓头、上框架、下框架的等效质量，c1、c2、c3分别为等效阻尼，k1、k2、k3分别为等效刚度。y1、y2、y3分别为垂向位移，Fl为气动抬升力。

1.3 弓网耦合模型

采用罚函数法对弓网系统进行耦合，设接触刚度为ks，则弓网接触力可表示为[12]：

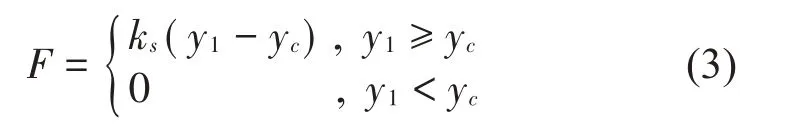
式中：yc为弓网接触点处对应的刚性接触网垂向振动位移。

2 动力学模型准确性验证

由于目前国内外暂时没有适用于刚性接触网动力学模型验证的相关标准，因此为了验证本文建立的动力学模型的准确性，设置受电弓运行速度为80 km/h，将其与文献[13]中的广州地铁实测接触压力统计数据进行对比，其中实测数据经过了20 Hz 的低通滤波，对比结果见表1。不同的是，文献[13]采用ANSYS软件中的有限单元法进行接触网建模，而本文采用假设模态法进行接触网建模，所用的满足边界条件的简支梁模态函数的试函数为：

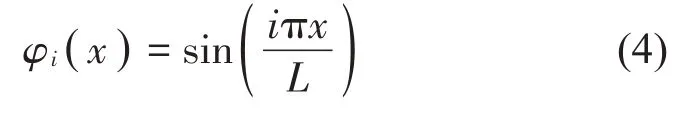
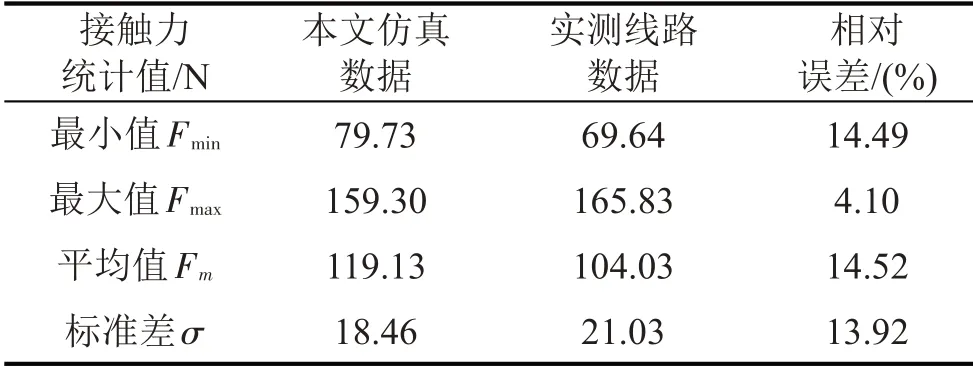
表1 80 km/h接触力统计值比较

模态截断阶数设为100 阶，仿真结果如图2所示。根据标准EN－50317[5]规定，在同等速度下仿真模型的结果与线路实测的结果误差不得超过±20%，由表1可知所建立的弓网仿真模型的相对误差最大值为14.52%，符合标准要求，由此表明本文的弓网动力学模型是可靠的。

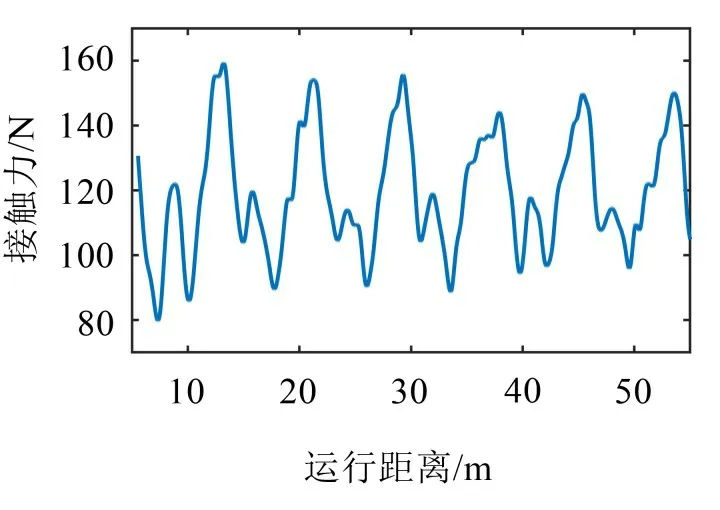
图2 模型验证接触压力仿真结果

3 受电弓参数敏度分析及优化

受电弓的参数是影响弓网系统动力学性能的重要因素之一。在已确定接触网结构及参数的条件下，如果受电弓的参数不匹配，不仅会导致弓网振动加剧、受流恶化、离线增加，还会带来受电弓滑板和接触线异常磨耗、钻弓、碰弓等一系列问题。因而，需要对受电弓参数进行优化设计，分析弓网参数是否匹配，定性了解弓头以及框架的质量、阻尼和刚度等参数对其动力学性能的影响，以获得最佳的受电弓设计参数[14]。

基于所建立的刚性接触网-受电弓三质量块模型，通过计算弓网系统的动力学特性，分析受电弓参数的敏度级别。以地铁CED125D型受电弓为例，其等效参数[2]见表2。

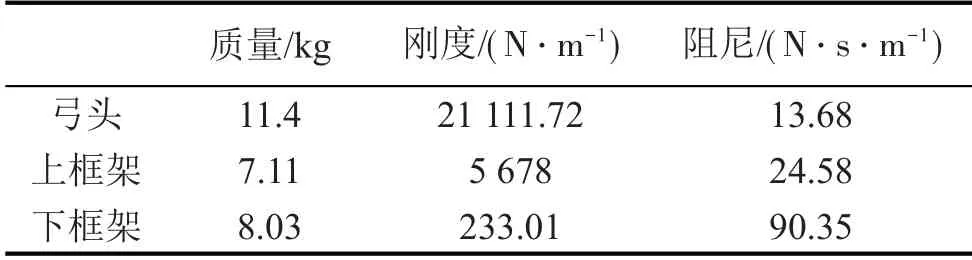
表2 CED125D型受电弓参数

设刚性接触网跨距为6 m、锚段长度为240 m，其余参数可参考文献[10]。在仿真过程中，设受电弓运行速度为120 km/h，静态抬升力为90 N，通过统计稳定段内的数据得到接触力标准差σ为10.09 N，最大值Fmax为107.36 N，最小值Fmin为61.61 N，平均值Fm为85.16 N。不同等效参数下仿真得到弓网接触力的时程曲线如图3所示。

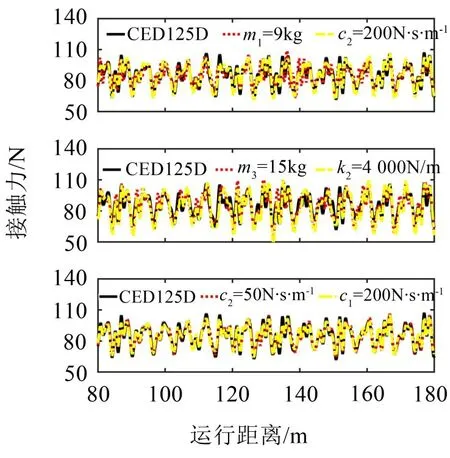
图3 不同受电弓参数下的接触力时程曲线

3.1 受电弓单参数敏度分析

假设受电弓三质量块模型的9个参数之间相互独立，采用控制变量法单独分析每个参数在给定范围内变化时弓网系统接触力的平均值、标准差、最大值和最小值相对于CED125D 型受电弓归算参数时的变化量ΔFm、Δσ、ΔFmax和ΔFmin。根据工程设计的可行性，假设受电弓弓头、上框架、下框架的等效质量分别可取为5 kg ～15 kg、3kg ～12 kg 和5 kg ～15 kg，等效阻尼分别可取0～50 N·s·m-1、0～50 N·s·m-1和40 N·s·m-1～240 N·s·m-1。等效刚度分别可取为15 000 N/m ～25 000 N/m、4 000 N/m ～8 000 N/m、100 N/m～360 N/m。

图4给出了受电弓9 个等效参数变化对于接触力平均值的影响。将每个归算参数xi除以其取值范围内的最大值xmax得到一个无量纲量xi xmax。

由图4可以看出，当上框架等效刚度k2与下框架等效刚度k3发生变化时，接触力平均值变化明显，且k3对于接触力平均值的影响程度大于k2。因此当k3或者k2发生改变时，应通过调整受电弓静态抬升力，以使得接触力平均值Fm恒定。而其他7 个等效参数的变化对于接触力平均值的影响较小，|ΔFm|≤0.31N，故当其发生改变时，保持静态抬升力不变，即可保证接触力平均值Fm恒定。

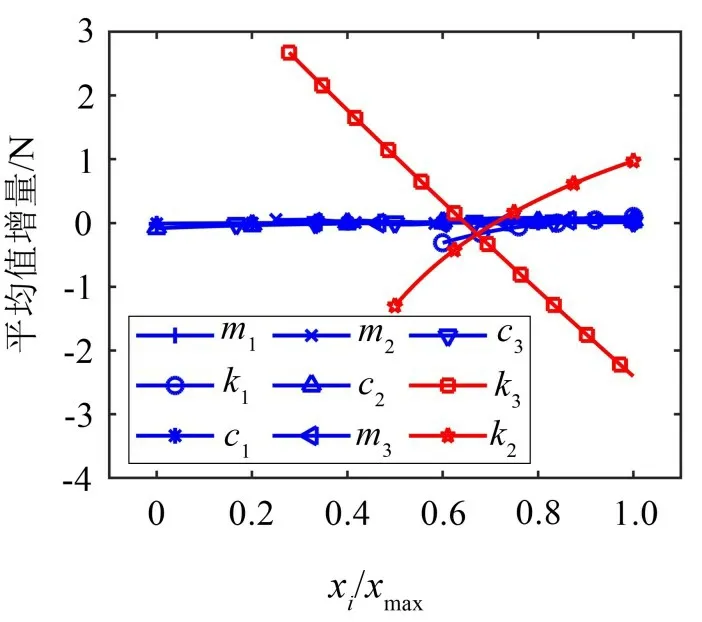
图4 三质量块参数对于接触力平均值的影响

图5为9 个受电弓等效参数对于接触力的Δσ、ΔFmax和ΔFmin的影响规律，以CED125D 型受电弓的标准参数为基准，优先关注引起Δσ＜0 的参数变化范围，当Δσ接近于0 的时候，再关注ΔFmax＜0 且ΔFmin＞0的参数变化范围。从图4可以看出，减小弓头等效质量，增大弓头等效阻尼或上框架等效阻尼都有利于提高受电弓接触网系统的耦合性能，提高受流质量，而增大上框架等效刚度和下框架等效刚度虽然减小了接触力的标准差，但造成接触力最小值也整体减小，易导致弓网离线，因而上框架等效刚度和下框架等效刚度不能过大，建议维持不变。

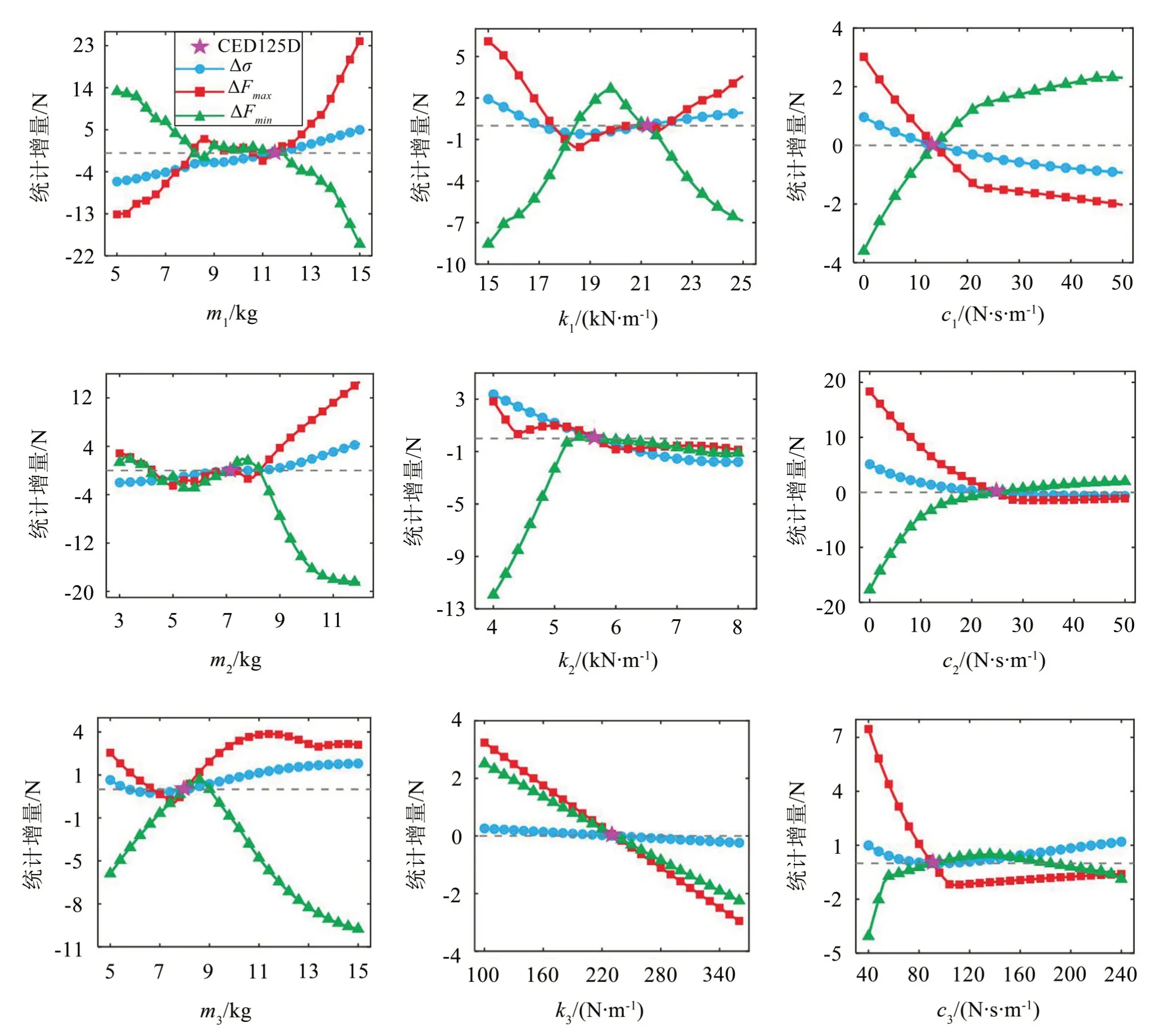
图5 三质量块单参数变化对于Δσ、ΔFmax和ΔFmin的影响

进一步分析当单个等效参数取最优时的接触力Δσ、ΔFmax和ΔFmin，图6给出了单参数变化时Δσ、ΔFmax和ΔFmin统计结果，可以看出m1取最优值5 kg时明显降低了接触力的标准差，减小了接触力的最大值且增大了接触力的最小值，提高了受流质量，故m1敏度评级为1，当m1=5 kg 时，Δσ=-6.10 N，ΔFmax=-13.10 N，ΔFmin=13.20 N。m2与k2也较为明显减小了接触力的标准差，Δσ约为m1取最优值时的1/3，但m2取最优值时增大了接触力的最大值，k2取最优值时减小了接触力的最小值，并非合适的等效参数优化选择，故其敏度评级为2。其他各参数敏度评级见表3。

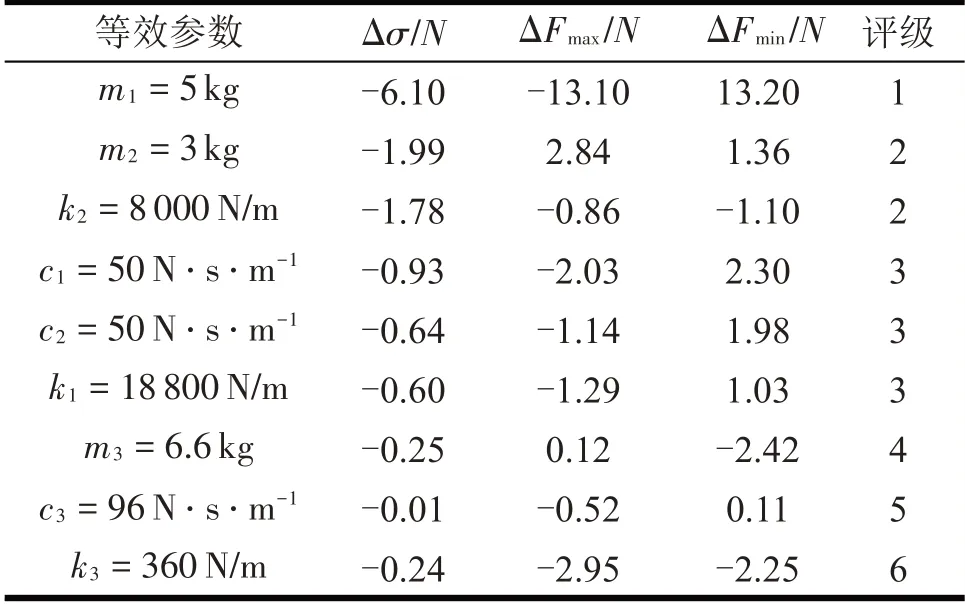
表3 单参数取最优时的敏度评级

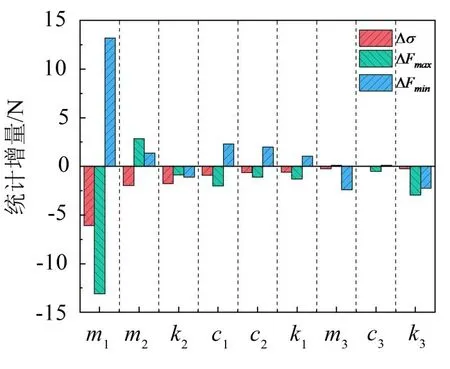
图6 单参数变化的Δσ、ΔFmax和ΔFmin统计

因此，若只进行CED125D 型受电弓单参数优化，建议取m1=5 kg，m2=7.11kg，m3=8.03kg，c1=50 N·s·m-1，c2=50 N·s·m-1，c3=90.35 N·s·m-1，k1=18 600 N/m，k2=5 678 N/m，k3=233.01N/m。

3.2 受电弓双参数敏度分析

从工程设计角度讲，调整弓头等效参数比调整框架等效参数易于实现，故本节分析受电弓弓头的3个等效参数两两联合变化对于接触力Δσ、ΔFmax和ΔFmin的影响结果，结果如图7所示，虚线代表0值，图7(a)、图7(d)、图7(g)代表Δσ，图7(b)、图7(e)、图7(h)代表ΔFmax，图7(c)、图7(f)、图7(i)代表ΔFmin。当m1与k1或m1与c1联合变化时结果见图7(a)至图7(f)，从中可以看出均是m1取最小值5 kg时Δσ最小，弓网耦合性能最好，此时k1取最小值15 000 N/m，c1取最大值50 N·s·m-1，这主要是因为弓头的等效质量m1的优先级最高，而弓头等效阻尼c1和等效刚度k1的优先级相对落后，m1占主导地位。当m1与k1联合变化时，Δσ=-6.94 N，ΔFmax=-14.91N，ΔFmin=15.08 N。当m1与c1联合变化时，Δσ=-6.47 N，ΔFmax=-14.41N，ΔFmin=14.72 N，两组参数联合变化对于接触力的影响结果类似，并且略微优于m1单参数变化时的Δσ=-6.10 N，ΔFmax=-13.10 N，ΔFmin=13.20 N。

进一步对优先级低于m1的k1和c1联合变化进行分析，其对于接触力Δσ、ΔFmax和ΔFmin的影响结果见图7(g)至图7(i)，从中可看出虚线右侧均有Δσ＜0，低于CED125D 型受电弓（对应图中的）的标准差，另外当c1=50 N·s·m-1，k1=18 600 N/m 时（对应图中的），σ取最优值为8.91 N，此时Δσ=-1.18 N，ΔFmax=-1.55 N，ΔFmin=2.25 N。统计双参数优化时的接触力Δσ、ΔFmax和ΔFmin如图8所示。至此可以看出，双参数优化时的优化结果好于单参数优化，这与文献[6]得出的结论一致。

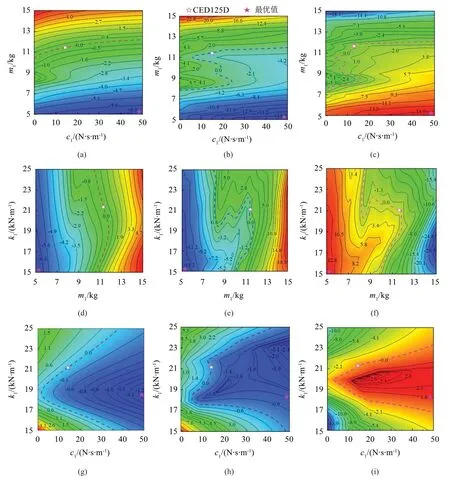
图7 三质量块双参数变化对于Δσ、ΔFmax和ΔFmin的影响

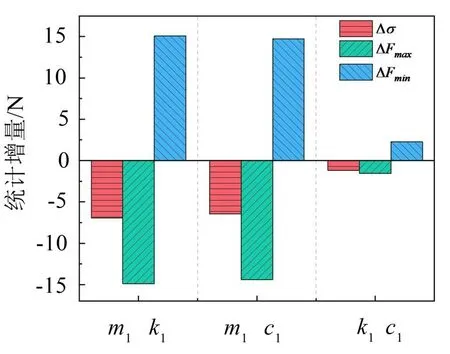
图8 双参数变化时的Δσ、ΔFmax和ΔFmin统计

另外，σ以及Fmax、Fmin随k1和c1的变化趋势不同，当k1一定时，随着c1的增大，σ与Fmax逐渐减小，而Fmin先增大后减小。当c1一定时，σ以及Fmax先减小后增大，而Fmin先增大后减小。

4 结语

建立城市轨道交通弓网系统动力学模型，采用控制变量法分析了CED125D 型受电弓三质量块模型9个等效参数的敏度评级，并分析了受电弓弓头3个等效参数联合变化对于接触力Δσ、ΔFmax和ΔFmin的影响，得到以下结论：

（1）弓头等效质量的敏度评级最高，上框架等效质量和上框架等效刚度次之，下框架等效刚度最低，且上框架与下框架等效刚度的改变相比于其他几个等效参数会明显影响接触力的平均值，故当其发生改变时需调整受电弓的静态抬升力使得Fm保持恒定。

（2）当m1与k1或m1与c1联合变化时，m1均取最小值5 kg 时弓网系统的耦合性能最好，此时k1取最小值15 000 N/m，c1取最大值50 N·s·m-1。通过弓头等效刚度k1和等效阻尼c1联合变化取最优值时，接触力标准差降低了1.18 N，最大值降低了1.55 N，最小值增大了2.25 N，3种双参数优化方案均呈现出比单参数优化更好的优化结果。

（3）由于城市轨道交通与干线铁路采用的接触网与受电弓不同，会呈现出完全不同的优化方案，因此，对于不同的接触网线路与受电弓类型还需进行不同的分析，本文的参数优化讨论可为城市轨道交通弓网系统设计、选型和评价提供参考。