基于CEEMDAN-TSMPE-PCA风力发电机齿轮箱高速轴承故障诊断技术

张玉兰，张宏伟，王新环

（河南理工大学 电气学院，河南 焦作 454003）

随着我国风力发电行业的发展，风电并网份额不断增大，风力发电机组故障轻则影响自身安全，重则引起电网动荡。据研究数据表明，风力发电机系统的故障中20%来源于齿轮箱，其中多数为轴承故障[1]。齿轮箱内部包含包括轴、齿轮以及轴承等零件，其中滚动轴承高速轴通常工作转速在每分钟千转以上，故障隐患较大，且其故障直接影响风力发电机的电能质量，使得并网难度提升。为此，针对风力发电机齿轮箱高速轴承进行故障诊断研究。

滚动轴承振动信号具有非线性、非周期性等特征，传统的时域、频域分析算法对此类非线性、非周期信号的分析效果不理想，因此非线性分析算法得到大量关注。Huang 等提出了经验模态分解(Empirical Mode Decomposition，EMD)，它降低了由于人为因素造成的算法分解误差[2]。大量学者的研究发现，由于EMD理论存在缺陷，使得所分解信号存在模态混叠现象。集合经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)是EMD的改进算法[3]。该算法通过在原始信号中添加一个白噪声的方式来消除EMD 分解过程中的模态混叠现象，但是在EEND 的重构信号中却存在着大量的噪声残余。Torres 等提出一种新的改进算法CEEMDAN，该算法克服了EMD模态混叠问题，降低了EEMD的重构误差，是目前非线性信号分析中的研究热点之一[4]。

文献[5]中提出一种基于CEEMDAN 排列熵与支持向量机的螺旋锥齿轮故障识别方法。文献[6]中提出一种基于CEEMDAN 联合样本熵、自适应阈值的降噪方法。文献[7]中将原始振动信号通过CEEMDAN 分解，利用峭度值联合多尺度排列熵(Multiscale Permutation Entropy，MPE)进行故障特征提取，实现故障智能识别。CEEMDAN 算法克服了模态混叠问题，在非线性信号降噪方面取得了较好的效果，但依旧存在虚假分量与噪声残留问题。MPE 是一种评价时间序列随机性突变行为的有效方法，具有计算速度快、抗干扰性强的优点，适用于轴承故障信号特征向量提取，但随尺度因子增加，MPE算法中粗粒化时间序列会变得越来越短，使得时间序列信息损失。

针对以上问题，本文提出了一种基于CEEMDAN、峭度值-相关系数准则、TSMPE、PCA 的故障敏感特征提取方法。该方法利用CEEMDAN 的自适应降噪分解优势，结合TSMPE能有效反映多尺度时间序列突变特性的特长，实现故障信号特征提取，再经过PCA算法降维后得到故障特征向量。最后，采用IAFSA-SVM 多分类故障分类器，实现风力发电机齿轮箱高速轴承的故障诊断。

1 算法原理及步骤

1.1 CEEMDAN算法原理及其降噪重构

1.1.1 CEEMDAN算法原理

CEEMDAN算法利用自适应噪声在保证数据的准确性和完整性的前提下，克服了模态混叠的问题，提高了运行效率，节省了计算成本[4]。具体描述如下：

(1)将满足N(0,1)分布的白噪声wi(t)添加到原始信号y(t)中，则第i次的信号可表示为

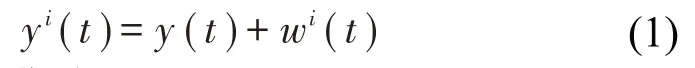
其中：t为添加高斯白噪声的次数，其中i=1，2，…，N。对信号yi(t)进行EMD分解，只保留第1阶模态分量IMFi1，其他为残余分量r1(t)。

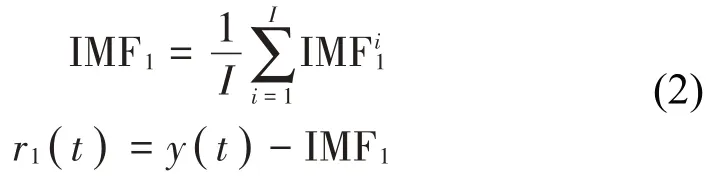
(2)将白噪声添加到残余分量r1(t)中：

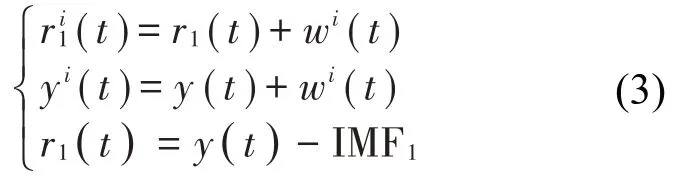
对ri1(t)进行EMD分解，得到第一个IMFi2,1。

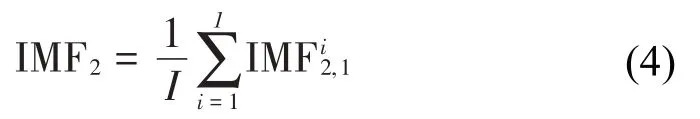
(3)重复以上分解过程m次，直至残差余量不适合被分解时停止分解，结束运算，信号y(t)可表示为：

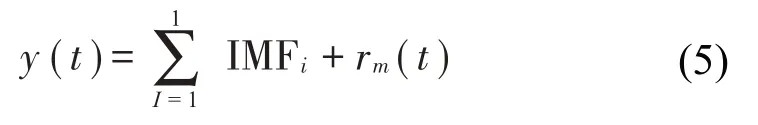
1.1.2 相关系数-峭度值准则信号重构

CEEMDAN算法通过添加自适应噪声克服了模态混叠现象，但在IMF 分量中仍然存在虚假分量及残余噪声问题。

相关系数是反映分解后的分量信号与原信号之间相关性的特征量，包含有主要故障信息的IMF 分量应与原信号的相关性较高，而虚假分量则相关性较差[8]。另外，文献[9]中的研究表明相关系数还体现了降噪信号与原信号的相似程度，相关系数越大，原信号所含噪声越小。为此，可以选择合理的相关系数参数，对虚假分量以及残余分量进行筛选。

轴承工作状态通常满足正态分布，峭度值反映随机变量分布特性的数值统计量，在正常工作状态，峭度值约为3，当含有冲击成分时，峭度值远大于3，峭度值越大，冲击信号越明显，包含故障信号越多。为此，通过相关系数-峭度值准则对IMF信号进行重构。

1.2 时移多尺度排列熵算法原理

TSMPE 是PE 和MPE 的优化方法[10－12]。TSMPE对数据长度的依赖性更小且鲁棒性更好，它可以更有效地分析时间序列，克服PE只能在单一尺度上描述信号复杂性这一缺点，同时也解决了MPE随尺度因子增加，粗粒化时间序列变得越来越短，导致时间序列信息损失的问题，具体算法如下。

（1）给定尺度因子τ，原始时间序列X={x1，x2，…，xn}可以根据式(6)进行定义：

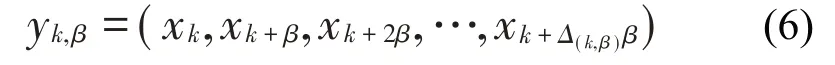
式中：k表示时间序列的起点，β表示时间序列的区间，Δ(k,β)表示上边界，0＜k＜τ，β=τ，Δ(k,β)=(N-β)/k，且k、β、Δ(k,β)都为整数。

（2）计算每个时移粗粒度时间序列的概率密度函数，其中尺度因子τ≥2。每个时移粗粒度时间序列的不同概率密度函数的平均值为：

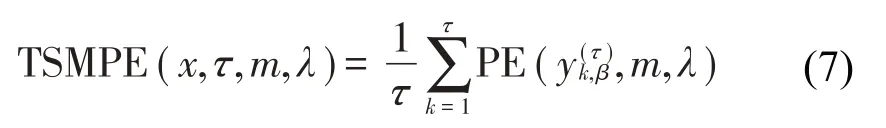
其中：m是嵌入维数，λ是延迟时间。

1.3 改进人工鱼群优化SVM算法

支持向量机算法在解决小样本、非线性、高维模式识别中具有许多特有优势[13]。SVM 算法中惩罚因子C、RBF 核参数G两个参数的大小对模型的预测效果有很大影响，选择合适的(C，G)组合至关重要。为此，通过改进人工鱼群算法对(C，G)寻优，提高故障诊断模型识别率。

人工鱼群算法（AFSA）是一种基于鱼群觅食的仿生智能算法[14]。传统人工鱼群算法选用固定步长，较大的步长会导致在寻优后期最优解的精度低，较小的步长会导致收敛速度较慢。因此，引入了调整函数来优化人工鱼的步长参数[15]。人工鱼步长参数如下。

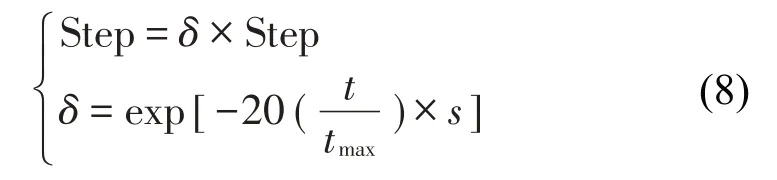
式中：δ为调整函数，Step 为人工鱼初始步长，t为迭代次数，s为正整数，且本文中s=6。改进人工鱼群优化SVM算法步骤如下。

(1)导入故障向量。提取各状态40 组故障数据，随机分成两部分，每部分为20组，其中一部分为模型训练数据，另一部分为测试数据。

(2)初始化参数。确定SVM 参数组合(C、G)的范围，并设置人工鱼群参数，包括种群数量N、最大迭代次数Trynumber、视野Visual和步长Step。

(3)计算初始鱼类种群的食物浓度。选用SVM返回的均方根误差作为模型的目标函数，将其最小值选定为最佳组合，将最优值保存至公告牌。

(4)根据式(8)更新步长，每条人工鱼的行为随之更新。计算食物浓度，若当前浓度高于公告牌中的食物浓度，则进行替换，否则保持不变。

(5)判断Trynumber 的大小，若当前迭代次数达到最大值，则将公告牌上最优参数组合(C、G)保存并输出；否则在迭代次数中添加1，然后跳转到第(4)步。

(6)输出最大准确率及其对应的(C、G)值。

2 故障识别方法

本文提出的基于CEEMDAN-TSMPE-PCA联合IAFSA_SVM 的风力发电机轴承故障诊断方法流程如图1所示。

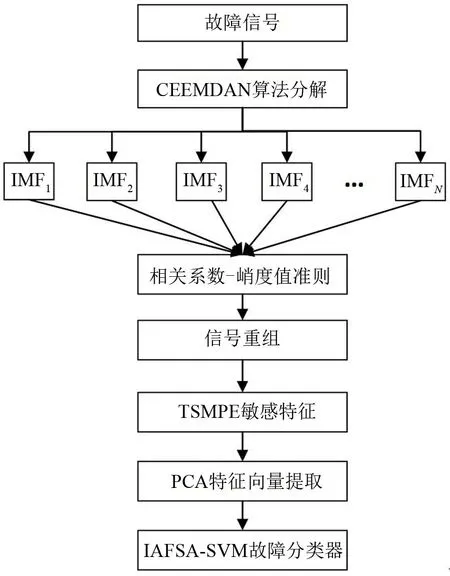
图1 风力发电机轴承故障诊断流程图

具体步骤如下：

(1)信号分解。对风力发电机轴承振动信号进行CEEMDAN分解得到N个IMF分量。

(2)信号重组。分别计算各个IMF 分量的相关系数、峭度值，基于相关系数-峭度值准则筛选符合要求的IMF分量进行信号重组。

(3)特征提取。对重组信号进行TSMPE 计算，获得维度为τ的排列熵值，对排列熵值进行PCA 降维，得到n维故障特征向量，其中τ和n均为正整数，且τ＞n。

(4)故障诊断。将故障特征向量作为IAFSASVM故障分类器的输入，实现风力发电机轴承故障诊断。

3 实验数据处理与分析

叶片捕捉风能通过转子轴心把能量传递给低速轴，低速轴经提速齿轮箱将能量传递到高速轴，高速轴连接着齿轮箱和发电机。高速轴采用一套圆柱滚子轴承和两套配对的圆锥滚子轴进行支承，在承受径向负荷时还承受不大的轴向负载，其始终保持在高速状态，转数区间为1 269 r/min～1 802 r/min，原理如图2所示[16]。

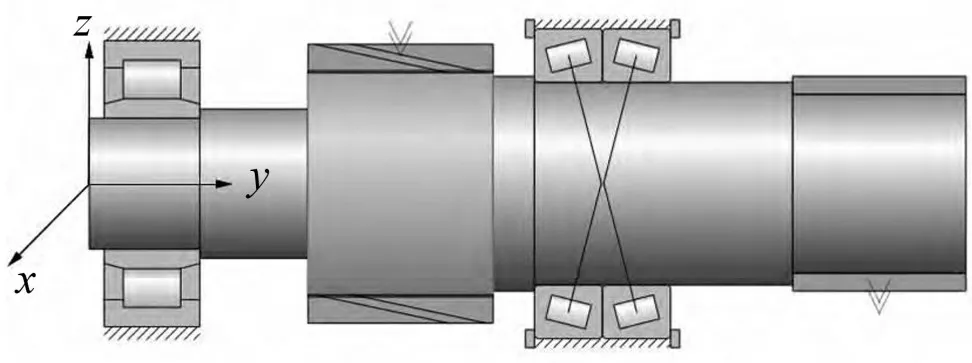
图2 风力发电机高速轴轴承布置

在凯斯西储大学轴承试验中，其待测的轴承位于电动机的两端，驱动端轴承型号为6205-2RS JEM SKF深沟球滚动轴承，风扇端轴承型号为SKF6203，其工作原理与风力发电机驱动链相似；另外，风力发电机高速轴转数区间为1 269 r/min～1 802 r/min，凯斯西储大学轴承数据集对应的转数分别为1 797 r/min、1 772 r/min、1 750 r/min、1 730 r/min。凯斯西储大学轴承试验台的驱动特性、转速都与风力发电机高速轴轴承相似，为此选用凯斯西储大学轴承数据对本文所提算法进行验证[17]。

表1 故障类型与故障代码

为验证本文算法在微弱故障诊断中的应用效果，选取轴承最小损伤直径为0.177 8 mm（0.007 英寸），故转速为1 730 r/min，采样频率为12 kHz，获得正常、滚动体故障、内圈故障、外圈故障这4 种状态下故障信号各40组，每组信号长度为2 048。

3.1 故障特征提取

为更直观理解特征提取的过程，以轴承内圈故障为例进行详细论述。随机选取一组内圈故障振动信号进行CEEMDAN 分解，分解之后得到一系列的IMF，阶数越大其频率越低，即包含的故障信息越少，具体如图3所示。

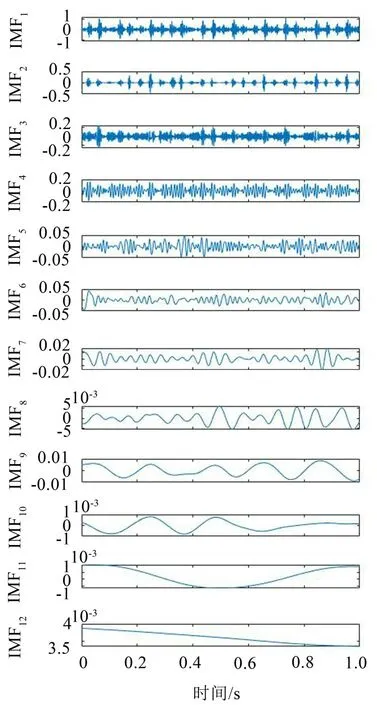
图3 CEEMDAN信号分解图

为准确提取故障信号较多的IMF 分量，选用峭度值-相关系数准则对各模态分量进行筛选。分别计算各个IMF的峭度值、相关系数，将峭度值大于3且相关系数大于0.1 的IMF 分量进行信号重组，各IMF分量峭度值、相关系数计算结果如表2所示。

从表2中可以清楚地看出，IMF1、IMF2、IMF3这3个信号分量都符合峭度值-相关系数准则的筛选条件。因此，选取这3个信号分量进行信号重构。此外，对原始信号和重构后的信号进行频谱分析，轴承内圈故障的重构信号时域图如图4所示，频谱分析如图5所示。

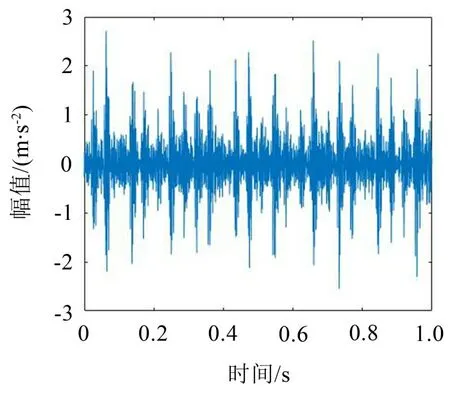
图4 CEEMDAN降噪后时域信号

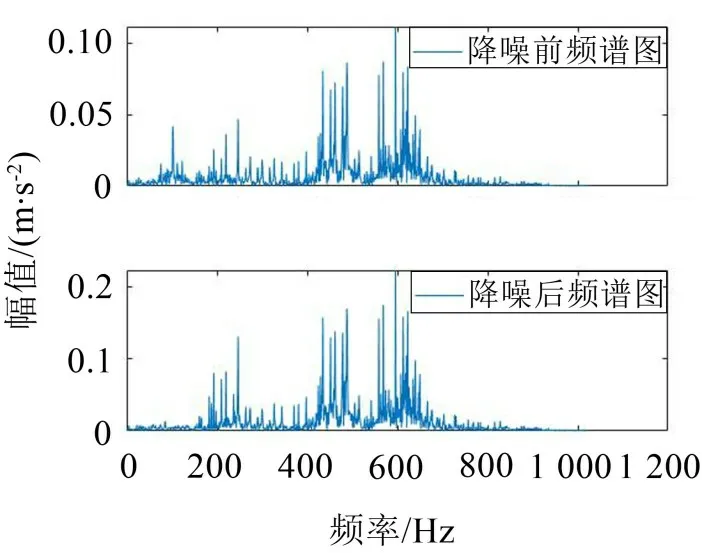
图5 CEEMDAN降噪前、后频谱对比图

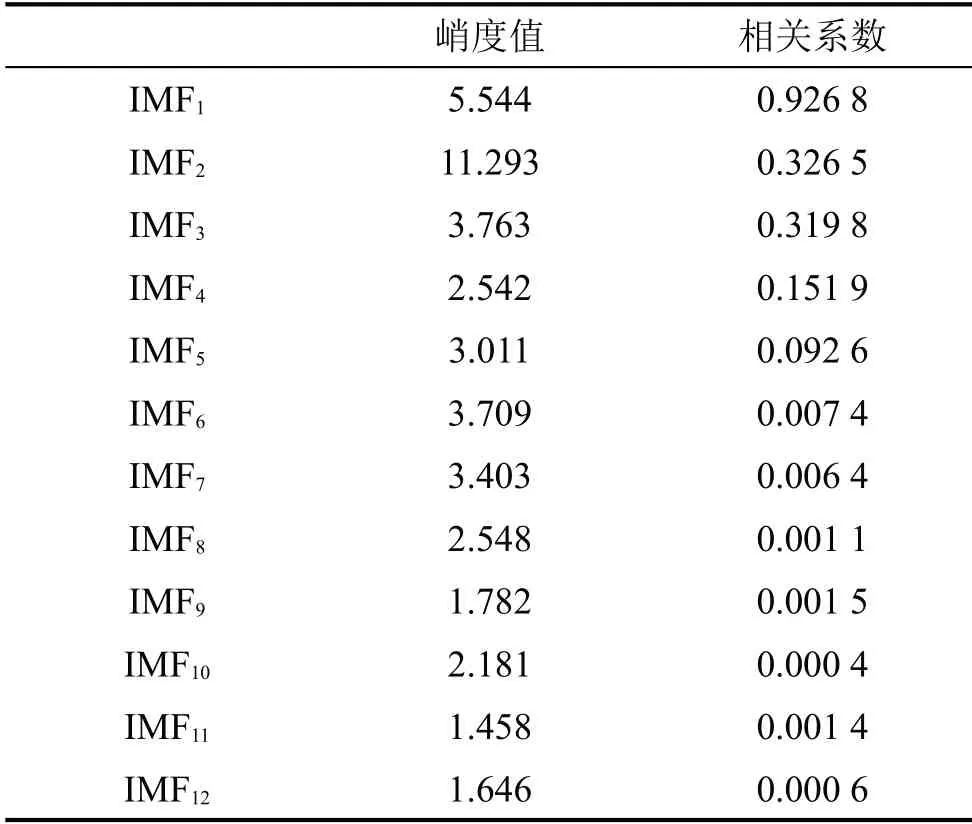
表2 各IMF分量峭度值-相关系数

从频谱图可以看出，重组信号保留了敏感故障特征，有效消除了噪声的干扰。为此，将重构后的信号作为后续分析的样本信号。同理，对其他状态下的故障数据进行上述降噪处理。

利用TSMPE对上述过程的重组信号进行分析，在计算TSMPE 敏感值时，需要考虑两个参数：嵌入维数m和时间延迟λ，针对这两个参数的选择其他学者已经做了大量分析[18]，由于篇幅原因不再赘述，在本文中嵌入维数m为6，延迟λ为1，尺度因子τ为20，数据长度n为2 048。4种状态下的TSMPE值如图6所示。

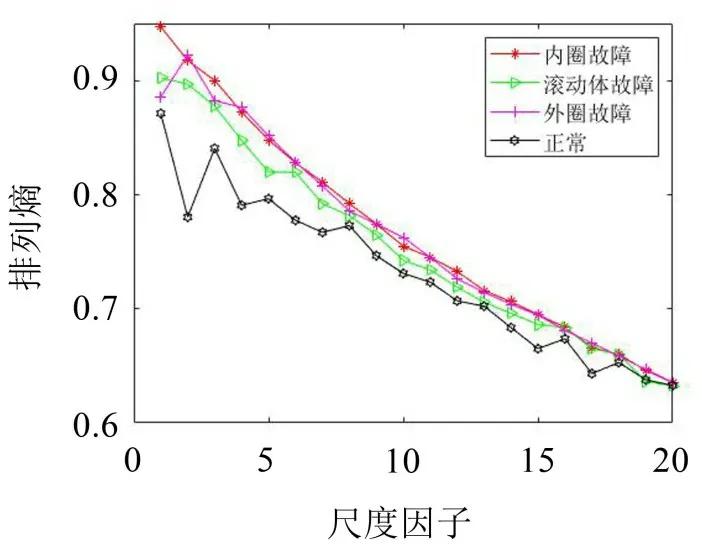
图6 4种状态下的TSMPE值

从图6可以看出，4 种状态下TSMPE 值的变换趋势大致相同，随着尺度因子的增加而降低，在尺度因子4～20区间内TSMPE值具有交叉重合的现象，故不能直接将TSMPE 值作为特征向量进行故障分类。为解决上述问题，对TSMPE 值进行降维，通过PCA 计算各个元素的贡献率，前3 个元素的累计贡献率达到99.02%，说明前3个元素包含了各状态下的大部信息特征。因此，选取这3 个元素作为特征向量，将原始20维特征值降到3维，有效减少了后续故障分类的计算量，实现数据去冗余，其贡献率如图7所示。

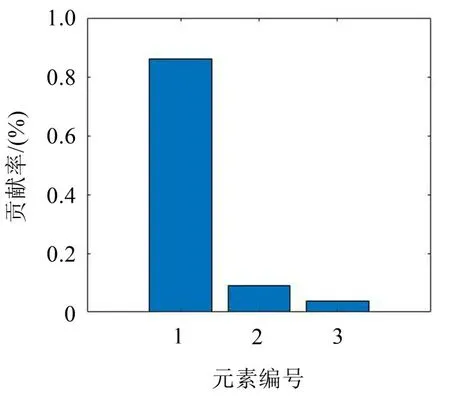
图7 主元素贡献率

3.2 滚动轴承故障诊断

用IAFSA 算法对SVM 的惩罚因子C及核函数G进行寻优。每种状态有40 组特征向量，将其随机分为两部分，每部分含20 组特征向量，其中一部分用于IAFSA_SVM 故障诊断模型训练，另一部分特征值被用于故障诊断，其中故障诊断模型训练时长为11 s，故障诊断时长为5 s，故障诊断准确率为97.5%，结果如图8所示。

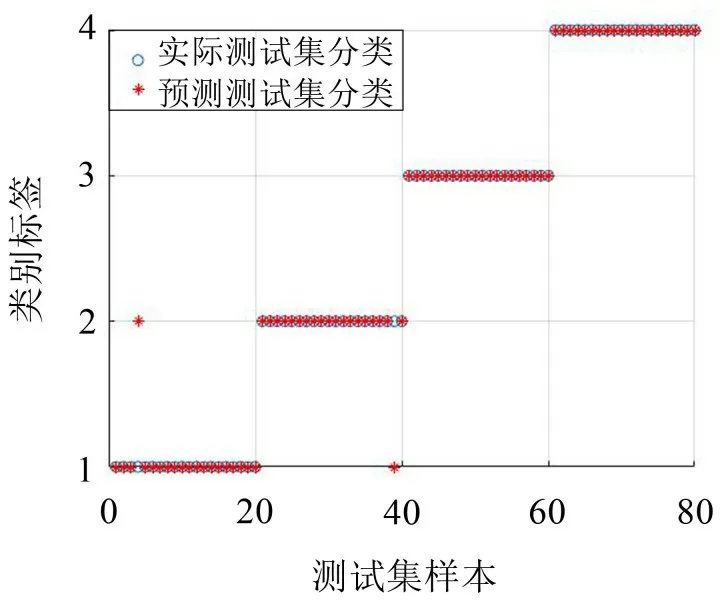
图8 CEEMDAN-TSMPE-PCA-IAFSA_SVM故障诊断结果示意图

3.3 方法对比

为验证本文所提故障诊断方法的优劣，从多个维度对算法进行对比验证。

3.3.1 特征提取维度进行对比验证

将本文所提CEEMDAN-TSMPE-PCA故障特征提取算法分别与EEMD-TSMPE-PCA故障特征提取算法以及CEEMDAN-TSMPE 故障特征提取算法进行对比验证。

将故障信号分别采用上述3种故障特征提取算法进行故障特征提取，将故障特征输入到IAFSA_SVM 故障诊断模型中进行识别，基于EEMDTSMPE-PCA 诊断结果如图9所示，基于CEEMDAN-TSMPE 诊断结果如图10所示，其故障诊断准确率如表3所示。

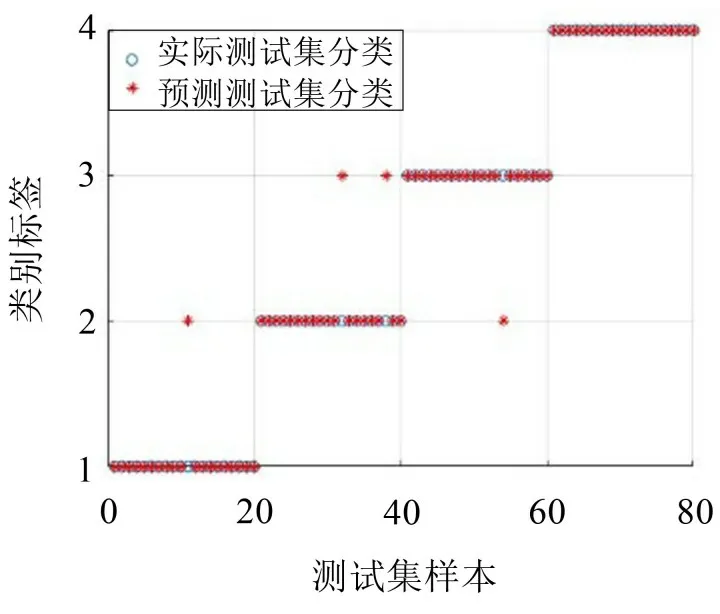
图9 基于EEMD-TSMPE-PCA故障诊断结果示意图

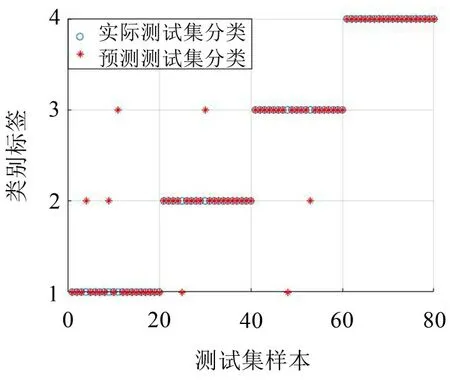
图10 基于CEEMDAN-TSMPE故障诊断结果示意图

由表3可知，经CEEMDAN-TSMPE-PCA 处理后的特征信号故障诊断准确率比经EEMD-TSMPEPCA 处理后的故障诊断准确率高，CEEMDAN 算法相较于EEMD算法在轴承故障信号特征提取方面效果更好，导致该结果的原因是经EEMD 提取的特征向量含有没有完全消除的噪声。此外，从表3可以看出由CEEMDAN-TSMPE-PCA特征提取算法处理后的故障诊断准确率为97.5%，高于由CEEMDANTSMPE 特征提取算法提取后的91.25%，从结果是可以看出经PCA 降维后的故障信息有效去除了信息冗余，故障信息更加明显，故障诊断的效果更好。

表3 基于3种特征提取算法故障诊断结果对比

3.3.2 故障训练模型维度对比验证

为证明IAFSA-SVM 故障诊断算法更有优势，将IAFSA_SVM 故障诊断算法、AFSA-SVM 故障诊断算法及PSO-SVM 故障诊断算法进行对比。选一组故障数据，经CEEMDAN-TSMPE-PCA 特征提取后，将特征向量分别输入到IAFSA-SVM、AFSA_SVM 和PSO_SVM 故障诊断模型中，其故障诊断结果如图8、图11、图12所示，具体故障诊断信息如表4所示。

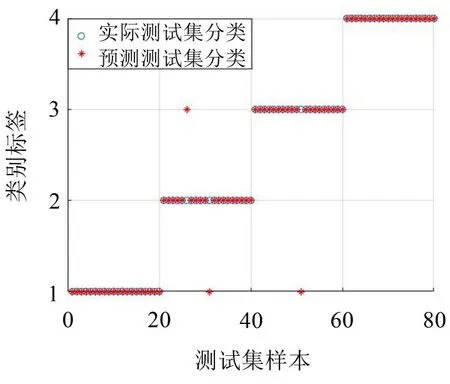
图12 基于CEEMDAN-TSMPE-PCA-PSO_SVM故障诊断结果示意图

由表4可知，相比于AFSA 和PSO，基于采用IAFSA 算法优化SVM 故障诊断算法故障诊断准确率更高，故障诊断耗时更短，可以说明IAFSA 对于惩罚因子C、核函数G寻优效果更好，基于IAFSA_SVM故障诊断算法在滚动轴承故障诊断中更有优势。

表4 故障诊断结果对比

通过多维度对比分析的结果可以看出，本文提出的方法要优于其他组合诊断的方法，在滚动轴承故障诊断方面具有一定的优越性。

3.4 风电场数据实验

为验证算法在实际中的效果，特对某公司在张家口市满井风电场1.5 MW 风电机组齿轮箱上采集的振动数据进行分析[19]。在运行过程中，发现齿轮箱高速侧出现振动变大的不良现象，通过内窥镜发现轴承高速端外环存在细小剥落点，2011年5月对故障部件进行更换，更换后发现轴承内环有一面积约50 mm×5 mm 大的剥落点，确定为内环故障。将部件更换前的振动数据看作故障数据，将部件更换后振动信号看作正常信号，某时段故障振动信号如图13所示。

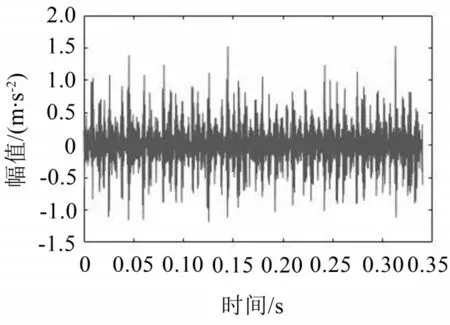
图13 风电场故障数据

根据本文所提出故障诊断方法的步骤对所有采集到的样本进行分析，首先对振动信号进行CEEMDAN分解得到9个IMF分量，其中IMF2、IMF3、IMF4分量峭度值大于3 且相关性系数大于0.1，将IMF2、IMF3、IMF4进行信号重组，实现初步降噪。接着对重组信号进行STMPE初始特征值提取，对提取后初始特征值进行PCA 降维，提取到40×3 的故障特征向量。

将特征向量输入到IAFSA-SVM 故障分类器中，其诊断结果如图14所示，其中轴承内圈故障状态编码为1，正常状态编码为2。

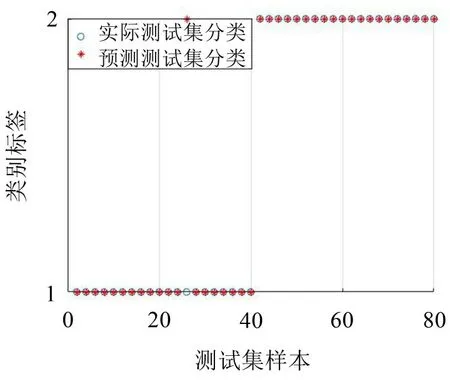
图14 基于风电场实际数据故障诊断结果

结果显示，故障诊断率为97.5%，说明本文提出的将CEEMDAN、TSMPE、PCA 相结合的降噪方法有效提高了风力发电机轴承故障诊断的准确率。

4 结语

综上所述，本文提出一种将CEEMDAN、TSMPE、PCA、IAFSA_SVM 相结合的轴承故障诊断方法，在风力发电机故障诊断中具有一定优势。

(1)利用CEEMDAN 算法对于非线性信号的分解优势，结合峭度值-相关系数准则实现故障振动信号的降噪、重构。采用凯斯西储大学轴承数据对算法进行验证，故障诊断率为97.5%。为进一步验证本文所提算法的实际应用效果，使用风电场实际故障信号进行再次验证，其故障诊断结果也为97.5%。说明了本文提出的将CEEMDAN、TSMPE、PCA 相结合的降噪方法在风力发电机故障诊断中的有效性。

(2)通过IAFSA 优化SVM 的惩罚因子C、RBF核参数G，减少了故障诊断模型的训练时长，提高了故障诊断准确率，最后故障诊断模型训练时长为11 s，故障诊断时长为5 s，故障诊断准确率为97.5%。

(3)由于故障发生的随机性，目前仅采集到正常状态及内圈故障状态的风力发电机齿轮箱高速轴振动信号。在用风电场实际数据对算法进行验证时，未能对除正常信号、内圈故障状态信号外的其他信号进行验证，待后期各故障数据量扩充后，可对其进行补充验证。

通过多维度的对比分析，说明了本文提出的方法要优于其他组合的诊断方法，在滚动轴承故障诊断方面具有一定的优越性。