轴承动载荷识别方法改进及试验验证

刘志强,陈亚明,沈德明,杨建刚,谭 平

（1.东南大学 火电机组振动国家工程研究中心，南京 210096；2.光大环境科技（中国）有限公司，南京 211106；3.南京科远智慧科技集团股份有限公司，南京 211102；4.江苏省热工过程智能控制重点实验室，南京 211102）

动载荷是影响旋转机械轴承性能的重要因素，准确识别轴承动载荷对于保证旋转机械的安全稳定运行至关重要。轴承动载荷很难直接测量获取，根据实测振动等数据识别轴承动载荷是研究热点。

动载荷识别方法主要有频域法和时域法[1]。时域法利用结构模态参数建立逆向时域模型，根据已知的动响应重构动载荷。时域法对初值非常敏感，误差累积难以避免且计算效率低[2]。频域法是在频域内构建系统逆向频响函数模型，再通过系统输出识别输入。频域识别方法包括：频响函数直接求逆法和模态坐标变换法。模态坐标变换法需要已知结构模态参数，在模态空间识别载荷的分布特性后，转换到物理空间[3]。该方法对模态参数识别的准确度要求较高，存在因模态截断所带来的误差。频响函数直接求逆法[4]简便，得到广泛应用。但是该方法存在测点和试验工况合理选取、矩阵病态等问题，导致解的不适定性。为了解决频响函数矩阵病态问题，人们开展了很多研究。Hansen[5]提出TSVD 法将较小的奇异值过滤，避免实测响应误差被过度放大。陈震等[6]在TSVD的基础上，提出基于分段多项式截断奇异值分解（Piecewise Polynomial Truncated Singular Value Decomposition，PPTSVD）识别桥梁移动载荷，算例表明该方法识别移动载荷精度高。夏超男、叶新茂[7－8]分别采用L 曲线法、广义交叉验证(GCV)法和通用交叉验证(OCV)法选取TSVD 模型中最优正则化参数。部分学者根据结构动力响应测试思路解决矩阵病态问题，姜金辉等、周林等[9－10]提出基于复合条件数权重法的测点优选模型，一定程度上可以减轻频响函数矩阵病态程度。杨帆等[11]基于模态函数分布创立了响应点筛选理论，适用于不同的载荷类型和边界条件。Gupta 等[12]利用D-最优设计结合有限元分析，确定最佳测点位置以提高载荷识别精度。

本文以发动机多支点轴承动载荷识别问题为对象，在基于条件数的响应点优化选择基础上，采用TSVD正则化方法消除矩阵病态性。在双转子试验平台上进行载荷识别试验，验证了该方法的有效性。

1 轴承动载荷辨识模型

对于实测的线性结构确定性响应，设实测响应点个数为m，待识别的载荷个数为n。动载荷列阵F(ω)与响应列阵U(ω)之间在频域上线性关系如式(1)所示：

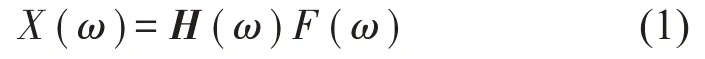
式中：H∈Cm×n，m≥n，H为系统的频响函数矩阵。动载荷可以表示为：

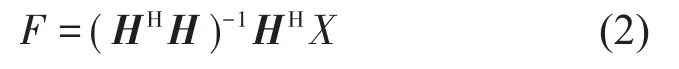
式中：上标“H”表示矩阵复共轭转置。

1.1 基于条件数的测点优化

不同响应点测点组合对应的频响函数矩阵不同，响应测点最优组合在于找到病态程度最低的频响函数矩阵。响应点个数对应频响函数的行数，载荷激励个数对应其列数，为保证解唯一，响应点个数不少于载荷激励个数[13]。

选取响应测点个数为mr(n≤mr≤m)，则测点选取共有种组合，对于第i种组合，对应的频响函数矩阵表示为Hi(mr×n)，其条件数可以表示如下：

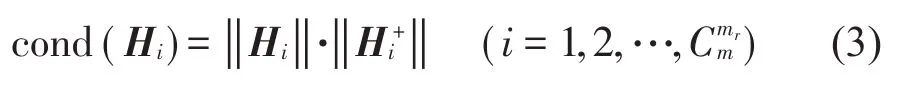
遍历所有测点个数下测点组合频响函数矩阵的条件数，找到条件数最小的矩阵，对应的响应测点组合即为最优方案。

1.2 截断奇异值分解技术（TSVD）

对频响函数矩阵H进行奇异值分解：

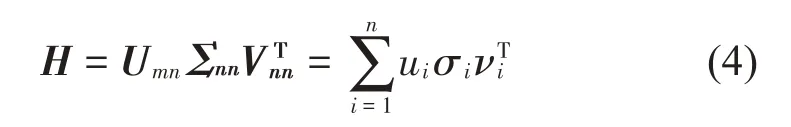
式中：Umn={u1,u2,…,un}和Vnn={v1,v2,…,vn}为列向量正交阵，是系统频响函数矩阵H分解出的两个酉矩阵，分别包括H矩阵奇异值左、右奇异向量；对角阵Σnn的对角元素{ }σi，i=1,2,…,n，σi≥0 是矩阵H的所有奇异值且按由大到小的顺序排列。将式(4)代入式(2)中，则得到F为：

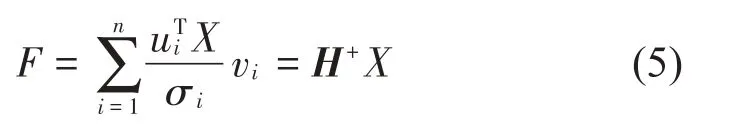
式中：上标“+”表示矩阵H的摩尔-彭诺斯广义伪逆，H+的表达式为：

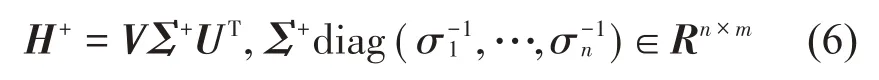
从式(5)可以看出，较小的奇异值会显著放大响应误差对参数估值的影响，使最小二乘解非常不稳定。截断奇异值分解(TSVD)法采用一个低秩矩阵Hk逼近原矩阵H，其中k＜n，目的是消除过小的奇异值及对应的特征向量对正则解带来的影响，由此削弱方程的病态特性，则式(1)的TSVD正则化解表示为：

式中：

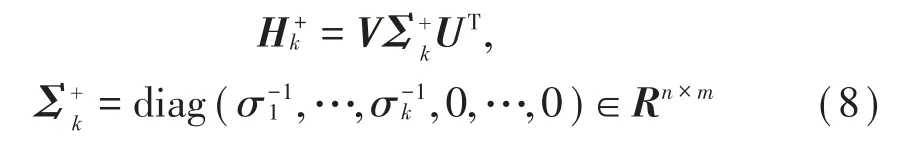
式中：Σk是将对角阵Σ中n-k个最小的奇异值过滤后得到的，当k取值合理时，矩阵Hk的条件数适中，使得TSVD 正则解更稳定，k称为截断数，使病态矩阵H转化为良态矩阵Hk。引入滤波因子：

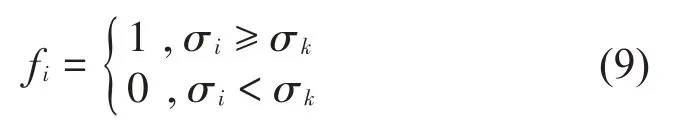
将式(8)代入式(7)中，正则化解表达为：

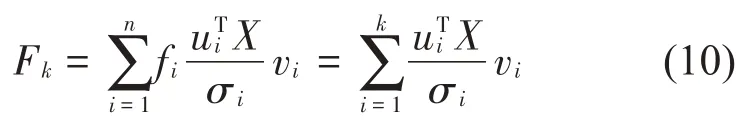
TSVD法的关键在于截断数k的选取，即确定合适的奇异阈值σk。在本文试验条件下，待识别载荷个数为3 个，分解后的奇异值矩阵中，只有3 个奇异值，大部分测点组合下最小奇异值占比不到10%，故取奇异值累积占比为90%，舍弃小奇异值，排除实际测试中响应误差的干扰。

2 轴承动载荷识别试验

2.1 试验台

在具有内外双机匣的双转子试验台上进行轴承支点动载荷辨识试验。试验台为带有高、低压转子的双转子结构，各支承通过锥壳和辐板连接到机匣上耦合在一起，机匣包括：进气机匣、风扇机匣、中介机匣、核心机匣和涡轮后机匣，机匣通过两个安装节安装在基座上。本文主要通过机匣水平方向振动，识别低压转子轴承水平方向动载荷。低压转子由#1、#2、#3共3个滚动轴承支承，其上带有2个轮盘，轴承支点动载荷主要由轮盘不平衡力引起，可利用轮盘进行动平衡实验。低压转子支撑模型和试验台实物图如图1所示。

图1 轴承支点动载荷识别试验装置

频响函数测试系统主要由加速度传感器、电荷放大器、力锤和信号分析仪组成。在频响函数测试试验时，激励由压电式力传感器产生，灵敏度为4.11 pC/N，力信号通过电荷放大器放大后传输到652u IOtech 动态信号分析仪中，电荷放大器的放大系数为1 mV/N；通过振动加速度传感器测量系统加速度响应，传感器灵敏度为100 mV/g，力信号和加速度振动信号由信号分析仪采集后被输入计算机，经计算得到位移频响函数。试验台运行时，使用振动数据采集仪获取机匣表面振动位移信号，采样样本长度设置为1 024，同步采样周期数为8。

2.2 实验方案设计

在低压压气机和涡轮轮盘上设置不平衡量，模拟不同动载荷工况，表1给出了7种试验工况。在保证试验安全下，使各工况之间机匣表面振动变化尽可能大。

表1 双转子试验台运行工况

在机匣表面布置10 个测点测量机匣响应作为系统响应，将低压转子所受不平衡力等效为3 个轴承所受激励并作为系统激励，低压转子测点布置如图2所示。拆除转子，分别敲击机匣表面的10 个测点，得到3个轴承支点的响应，再利用频响函数互易性，获得轴承支点到机匣表面10×3维加速度频响函数矩阵，相干系数大于0.7，认为频响函数可靠。

图2 试验台结构及测点布置

利用实测机匣响应和频响函数，识别出两种工况下3 个轴承支点动载荷矢量差，根据力和力矩平衡，计算出两个轮盘上不平衡力，将计算出的轮盘不平衡力矢量差与实际不平衡力矢量差对比，得到不平衡力的幅值和相位误差，平均幅值相对误差在15%左右，同时平均相位误差不超过20°，认为动载荷识别结果可靠[14]。

低压转子受力分析模型如图3所示，轮盘不平衡力求解方程见式(11)。

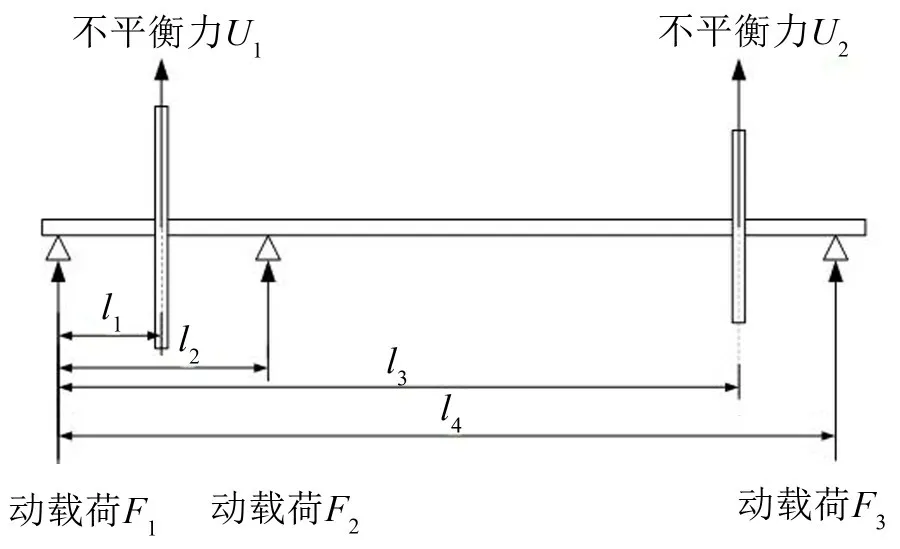
图3 低压转子受力分析模型

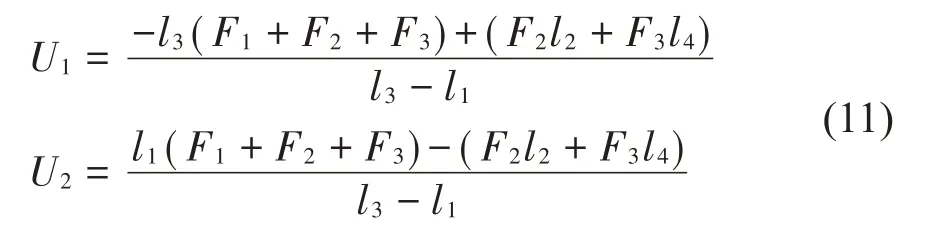
式中：U1和U2分别为低压压气机风扇轮盘和低压涡轮盘所受不平衡力；F1、F2和F3分别为#1、#2 和#3 轴承所受动载荷。

2.3 试验结果分析

以测点3为例，图4给出了转速为1 170 r/min和1 294 r/min时机匣表面该测点的振动原始波形和频谱图。试验转速1 170 r/min 接近临界转速1 200 r/min，与不平衡力同频的工频振动被大幅度激发出来，幅值较大，占据主导成分，导致振动波型比较规则。远离该转速区间，转速在1 294 r/min时，各种频率成分都存在，信号比较不规则，故选择转速1 170 r/min时进行分析。图5为通过锤击试验获得的各机匣与轴承支点的频响函数和相干系数，在10 Hz～30 Hz研究范围内相干系数大于0.85。

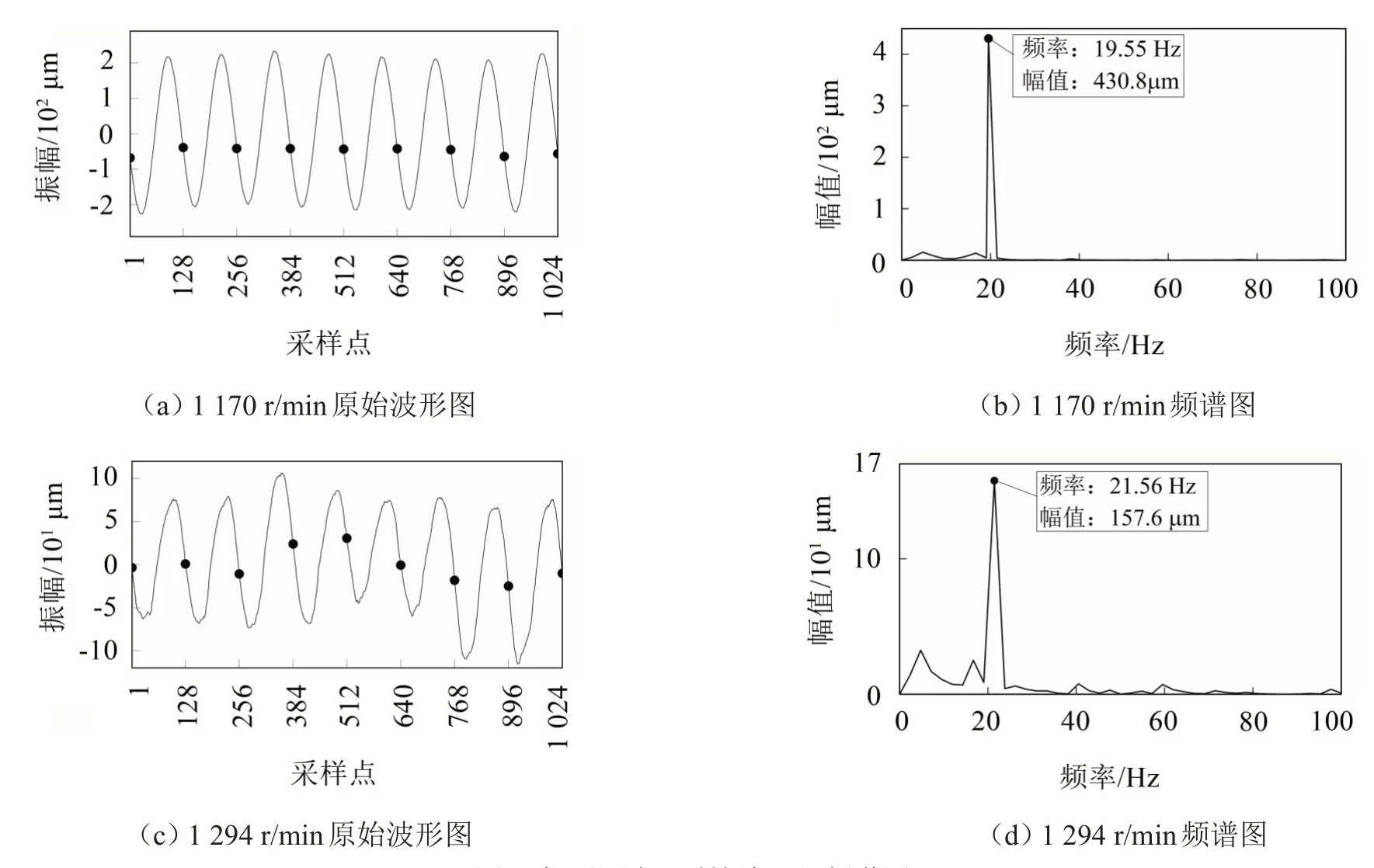
图4 机匣测点3原始波形和频谱图

图5 机匣-轴承频响函数曲线

为了验证最优响应测点选取方案识别载荷的准确性，试验中总共选取响应测点3个～10个，载荷识别个数为3，共有=968种可能的组合，并对每种组合情况计算其对应的频响函数条件数。图6给出了所有测点组合的条件数，表2为部分较小和较大条件数时的测点组合。

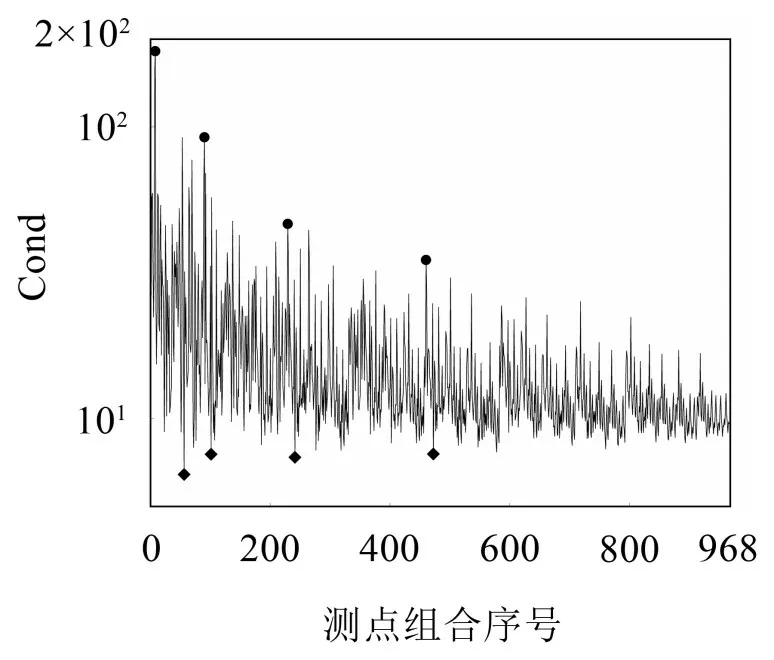
图6 不同测点组合对应的条件数

从表2可以看出：测点组合为2、6、8时最小条件数为6.4；测点组合为1、2、10时最大条件数为181.9。对比表中左右两列测点组合，当加入测点5、10 时，条件数较大，导致矩阵病态程度变大。选择响应点测点时应遵循以下原则：①避开机匣边缘处；②测点之间不能相距太近。选择低压压气机风扇机匣和核心机匣中部时，频响函数条件数更低，矩阵病态程度得到改善。

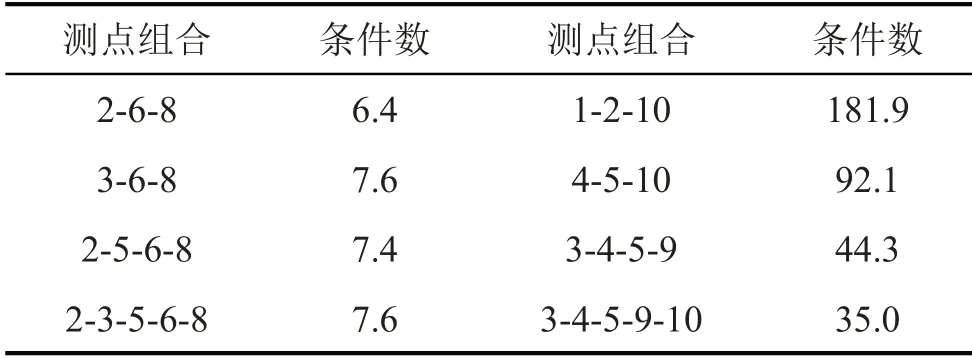
表2 部分测点组合条件数

对比不同载荷识别方法，选择6组对比工况，响应点分别选取机匣表面全部测点、对比测点组合2、5、6、8和优化测点组合2、6、8时，得到3个轴承支点动载荷识别结果，根据式（11）计算出加重轮盘不平衡力识别值，对比实际不平衡力和识别值获得载荷识别幅值和相位误差。

表3给出了选取机匣表面全部测点时，采用频响函数直接求逆法识别轴承动载荷结果；表4给出了选取机匣表面全部测点时，采用TSVD 正则化法识别轴承动载荷结果；表5给出了选取对比测点组合时，采用TSVD正则化法识别轴承动载荷结果；表6给出了选取优化响应点测点组合时，采用TSVD正则化法识别轴承动载荷结果。

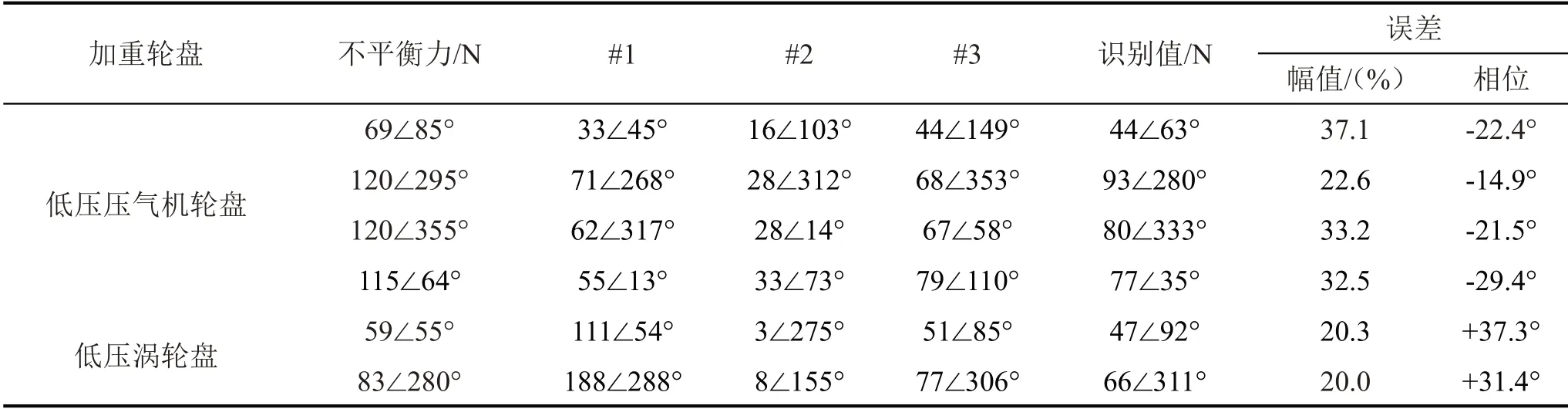
表3 全部测点-直接求逆

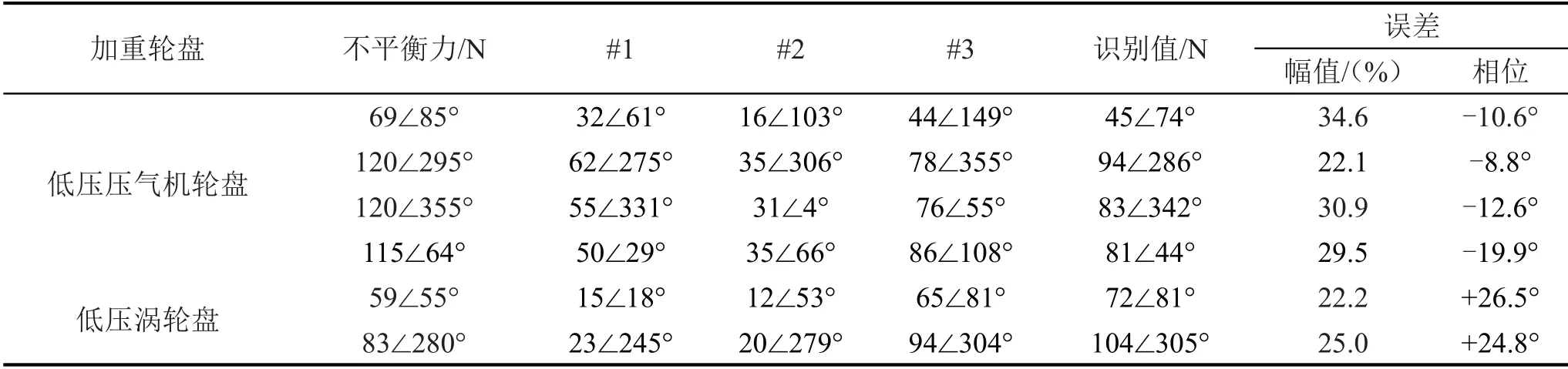
表4 全部测点-TSVD法

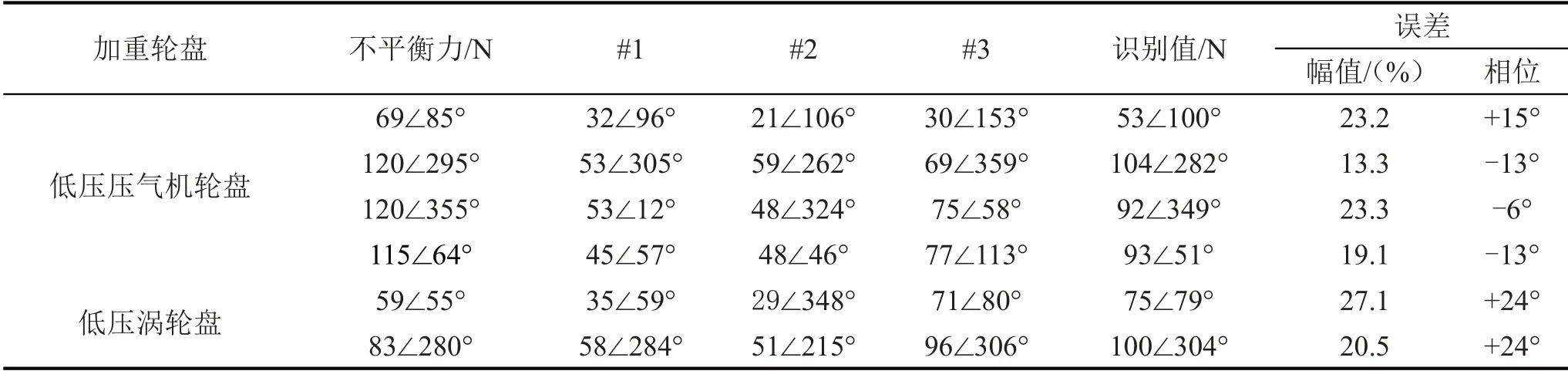
表5 对比测点-TSVD法

表6 优化测点-TSVD法

从表3可以发现，对比组合加入机匣边缘测点5时，由于与测点6距离较近，响应之间线性相关性变大，导致载荷识别误差比优化测点组合大，故只需选取其中一个测点即可，这进一步说明测点选取的合理性。综合采用基于条件数的响应点优化方法和TSVD 法能够改善频响函数矩阵的病态程度，提高轴承动载荷的识别精度。

3 结语

针对带机匣的多支承旋转机械轴承动载荷识别问题，采用频响函数直接求逆法识别载荷，建立TSVD 正则化和基于条件数的响应点测点优化相结合的方法，抑制该逆问题中矩阵的病态性。在双转子试验台上进行载荷识别试验，通过在轮盘上模拟不同不平衡工况，将低压转子所受不平衡力等效为轴承支点所受动载荷，验证载荷识别的准确性。结果表明：机匣响应点测点选取应避开结构边缘，采用测点组合优化后的TSVD方法可以有效减弱频响函数矩阵的病态性，使轴承动载荷识别结果更准确。