减振镗杆系统非线性动态特性与吸振能量研究

杨 杏，韩 威，石建飞

（1.陕西铁路工程职业技术学院 铁道装备制造学院，陕西 渭南 714000；2.兰州理工大学 机电工程学院，兰州 730050）

减振镗杆被广泛应用于深孔加工中，在机械制造工艺中占有重要地位。减振镗杆工作时振动产生的能量主要通过其内部质量块的往复振动吸收，从而达到减振的目的[1－2]。镗杆与工件接触产生的颤振严重影响产品加工质量[3]，高精密智能制造的发展对减振镗杆系统的精度、平稳性和可靠性提出了更高的要求。因此，研究减振镗杆系统振动问题，对其结构优化设计与加工质量提高极为重要。

国内外对减振镗杆系统减振性能进行了大量的研究，Lee等[4]利用复合材料设计了具有较强抗颤振性能的阻尼镗刀杆，分析了其动态特性；秦柏等[5]建立了减振镗杆系统的多柔体动力学模型，分析了弹簧刚度和黏性阻尼对镗杆振动幅值的影响；何全文等[6]建立镗杆系统有限元模型，分析了镗杆谐响应特性和幅频特性；向文英[7]借助有限元法研究了减振镗杆系统的动力学特性，并对影响系统振动的相关参数进行优化，得到减振效果较优的力学参数；罗红波等[8]建立3自由度减振镗杆系统力学模型，研究了外界激励频率对镗杆振幅的影响，但忽略橡胶圈和阻尼液等非线性因素的影响。在非线性动力学方面，闫俊霞等[9]对摩擦耗能镗杆的原理进行了分析，建立了包含非线性库仑干摩擦的数学模型，并以摩擦参数为变量，通过数值仿真方法研究了模型的吸振性能。杨月婷[10]提出了半主动动力吸振镗杆系统，将磁流变液应用于镗杆的减振装置，着重分析其非线性因素对减振镗刀杆振动特性的影响。石建飞等[11－12]考虑橡胶圈和阻尼液非线性因素的影响，研究了减振镗杆系统的安全盆分岔与侵蚀机理，分析了两自由度和三自由度减振镗杆系统的分岔与混沌特性。很多学者对减振镗杆系统的动态性能和非线性动力学进行了大量研究，并取得了很多有价值的研究成果，但忽略了在镗杆内部橡胶圈和阻尼液等耦合作用下振动刚度的时变特性，对内部质量块吸振能量的变化规律鲜有研究，双参数关联下镗杆系统非线性动态特性和吸振能量分布特性也未见报道。

本文考虑镗杆内部橡胶圈和阻尼液的非线性因素及其在耦合作用下的时变刚度特性，建立两自由度减振镗杆系统非线性动力学模型，研究减振块质量和外激励频率对系统非线性动力学特性的影响以及减振块吸振能量的变化规律，并基于双参数分析法[13]，研究减振块质量和外激励频率的关联作用对镗杆系统非线性动力学特性和吸振能量的影响。

1 两自由度减振镗杆系统动力学建模

减振镗杆系统的结构示意图如图1所示[12]，其主要由镗杆杆体1、垫片2、橡胶圈3、阻尼液4、减振质量块5、堵块6、刀头7和紧固螺钉8组成。镗杆振动产生的能量主要被内部质量块5 吸收，从而可减小镗杆振动。为方便动力学建模与分析，将镗杆杆体1、垫片2、堵块6、刀头7 和紧固螺钉8 作为主系统，其质量为M1，令K1和C1为主系统的刚度和阻尼；以橡胶圈3、阻尼液4、减振质量块5 为减振单元，令M2、K2和C2分别为其质量、刚度和阻尼。图2为减振镗杆系统简化物理模型，其中Fcos(Ωτ+Ψ)为系统外激力。

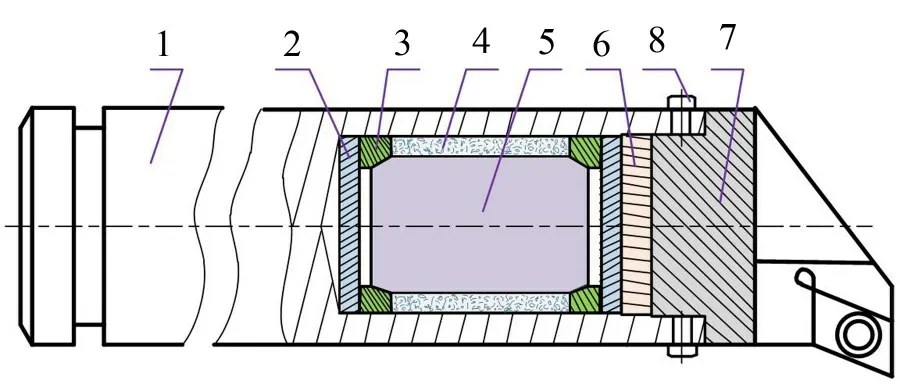
图1 减振镗杆系统结构示意图

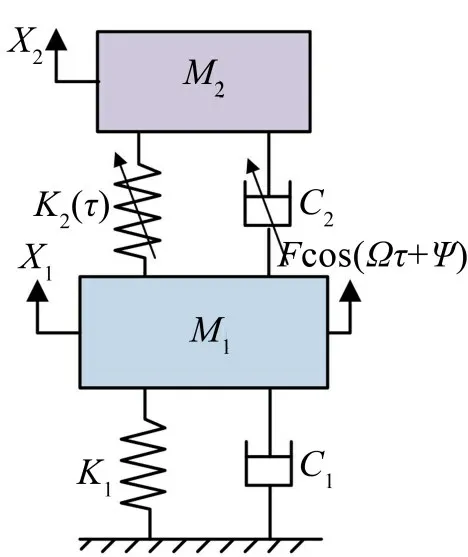
图2 减振镗杆系统简化物理模型

由于阻尼液和橡胶圈的耦合作用，减振块振动刚度和阻尼呈时变性和非线性[14－15]。为便于计算和分析，减振块时变刚度可被表征为1 阶谐波函数的形式，K2(τ)=Km+Knsin(Ωτ+Ψ)，式中Km和Kn分别为平均刚度和时变刚度波动系数。减振块非线性时变弹簧力Fe可表示为：

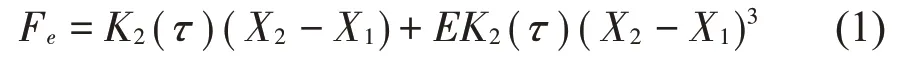
其中：E为小参数。减振块非线性阻尼力Fd可由式(2)计算得到。

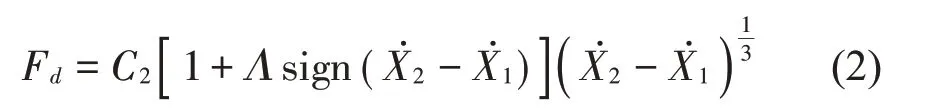
式中：Λ为非对称系数，表征减振器复原行程与压缩行程阻尼力的不相等度，sign(·)为符号函数，可由式(3)表示。

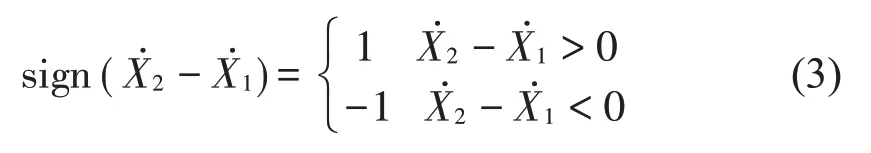
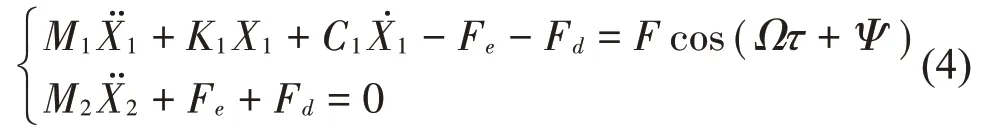
根据集中质量法，减振镗杆系统的非线性动力学模型如下：将式(1)和式(2)代入式(4)，并令初始位移D=X1(0)为长度尺度，T1=为时间尺度，定义以下无量纲量：

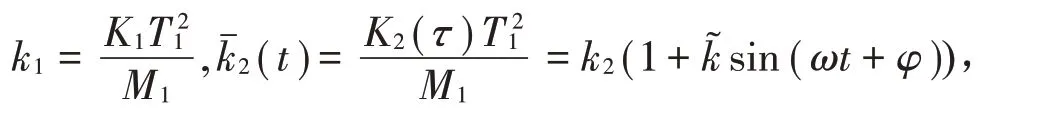
则，方程式(4)的无量纲形式为：

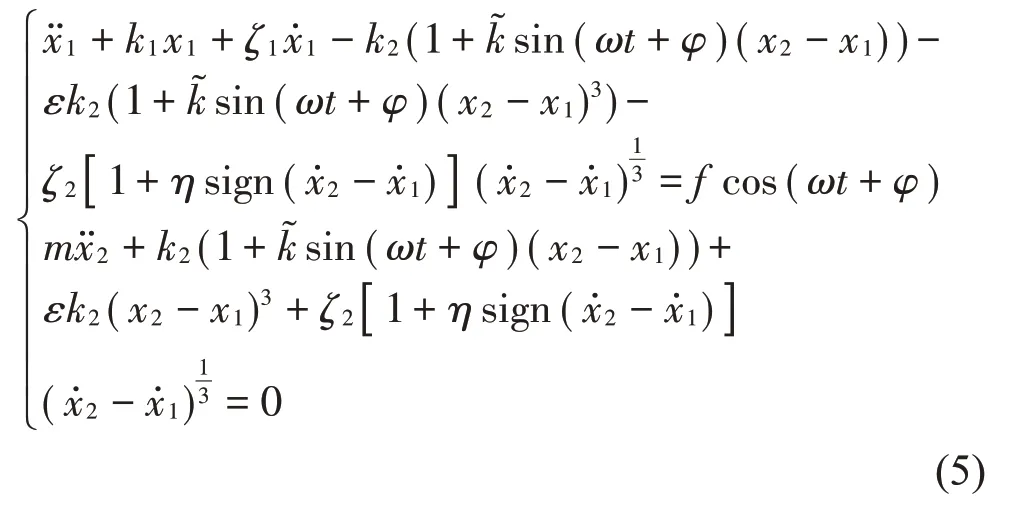
2 参数影响下减振镗杆系统非线性动态特性分析

减振块质量和外激励频率对镗杆系统的减振性能有重要的影响。本文基于变步长4阶Runge-Kutta法研究减振块质量比m=M2/M1和外激励频率ω及其相互关联性对镗杆系统非线性动态特性的影响。

2.1 单参数变化的影响

（1）减振块质量比m的影响

令外激励初始相位角Ψ=0.0，取系统无量纲参数k1=0.2、k2=0.1、ζ1=0.01、ζ2=0.09、ε=0.1、ω=0.75、η=0.428 6、f=1.5，令减振块质量比m为控制参数，图3为镗杆杆体振动位移x1随质量比m增大的分岔图与对应最大Lyapunov指数谱图（TLE）。稳定周期运动的TLE 值小于0，混沌运动的TLE 值大于0，准周期运动的TLE值在0附近上下波动。

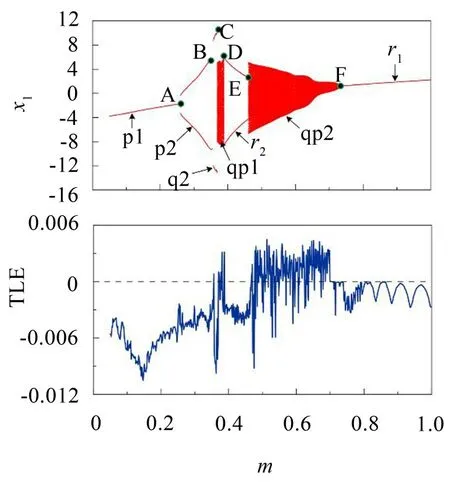
图3 随m增大的分岔图与相应TLE谱

当m较小时（A点左边），系统虽表现为稳定的周期1运动p1，但其振动幅值相对较大，如图4（a）所示，其中曲线表示相轨迹，品红色圆点表示Poincaré映射点（下同）。随着m增大，p1在A点倍化为周期2运动p2，随后p2在B点经过一次周期跳跃转迁为另一种周期2 运动q2，p2 与q2 的相轨迹拓扑结构不同，且q2的轨迹相对扩大，见图4（b）和图4（c）。

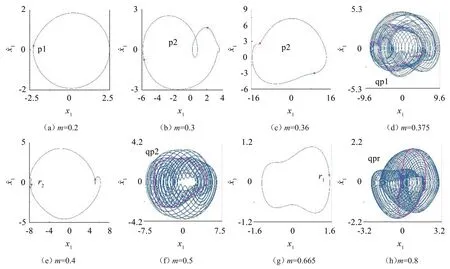
图4 系统相图和Poincaré映射图

q2 在C点进入准周期运动qp1，qp1 在较小的m范围内存在，在D点退化为周期2运动r2，qp1与r2的相轨迹和Poincaré 映射图见图4（d）和图4（e）。随后，r2在E点再次转迁为准周期运动qp2，且随m的增大qp2 运动振动幅值不断减小，见图4（f）和图4（g）。qp2 在F点退化为稳定的周期1 运动，且振动幅值减小，见图4（h）。

可见，减振块质量比m对系统的振动有重要的影响，当m较大（F点右边）或较小时（A点左边），系统表现为稳定周期1 行为，但m较小时系统振动幅值较大，制约产品加工精度；m在0.3～0.7附近时，系统出现分岔和准周期行为，镗杆振动相对复杂。故在减振镗杆系统设计中，在满足尺寸参数条件下应尽可能采用大质量的减振块，以减小镗杆振动。

（2）外激励频率ω的影响

令外激励频率ω为参数变量，取m=0.55，剩余参数与图3中保持一致，图5为镗杆系统振动位移x1随ω增大的分岔图及相应的TLE 谱图。图6为与图5相对应的相图和Poincaré映射图。

图5中，当ω较小时系统表现为准周期运动qp1，其Poincaré 映射图为极限环，见图6（a），随后qp1 退化为周期3 运动，见图6（b），该周期3 在ω极小范围内存在，随后该周期3 运动转迁为准周期运动qp2，其Poincaré映射图为3个极限环，见图6（c）。随着ω的增大，qp2 退化为周期1 运动p1，p1 在A点发生周期跳跃，并转迁为不同的周期1运动q1，且振动幅值减小，见图6（d）和图6（e）。

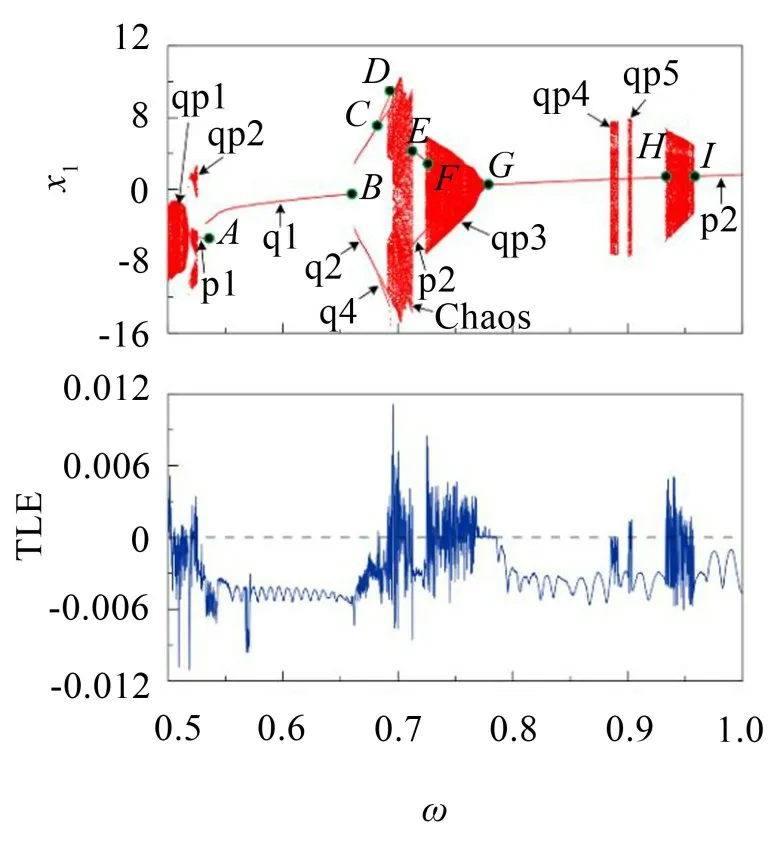
图5 随ω增大的分岔图与相应TLE谱

q1 在B点倍化为周期2 运动q2，随后q2 在C点倍化为周期4 运动q4，q4 在D点进入混沌（Chaos），相轨迹和Poincaré映射如图6（f）至图6（h）。混沌运动在E点退化为稳定的周期2 运动p2，见图6（i）。随后，p2 在F点进入准周期运动qp3，且随着ω的增大，qp3的相轨迹不断缩小，系统振动幅值减小，见图6（j）至图6（l）。qp3在G点退化为稳定的周期1运动r1，在G和H点之间系统出现准周期运动窗口qp4和qp5，在H和I点之间出现准周期运动qp6，其Poincaré映射图表现为扭曲的闭合曲线，见图6（m）。图6（n）为r1的相轨迹和Poincaré 映射图，其振动幅值相对较小。

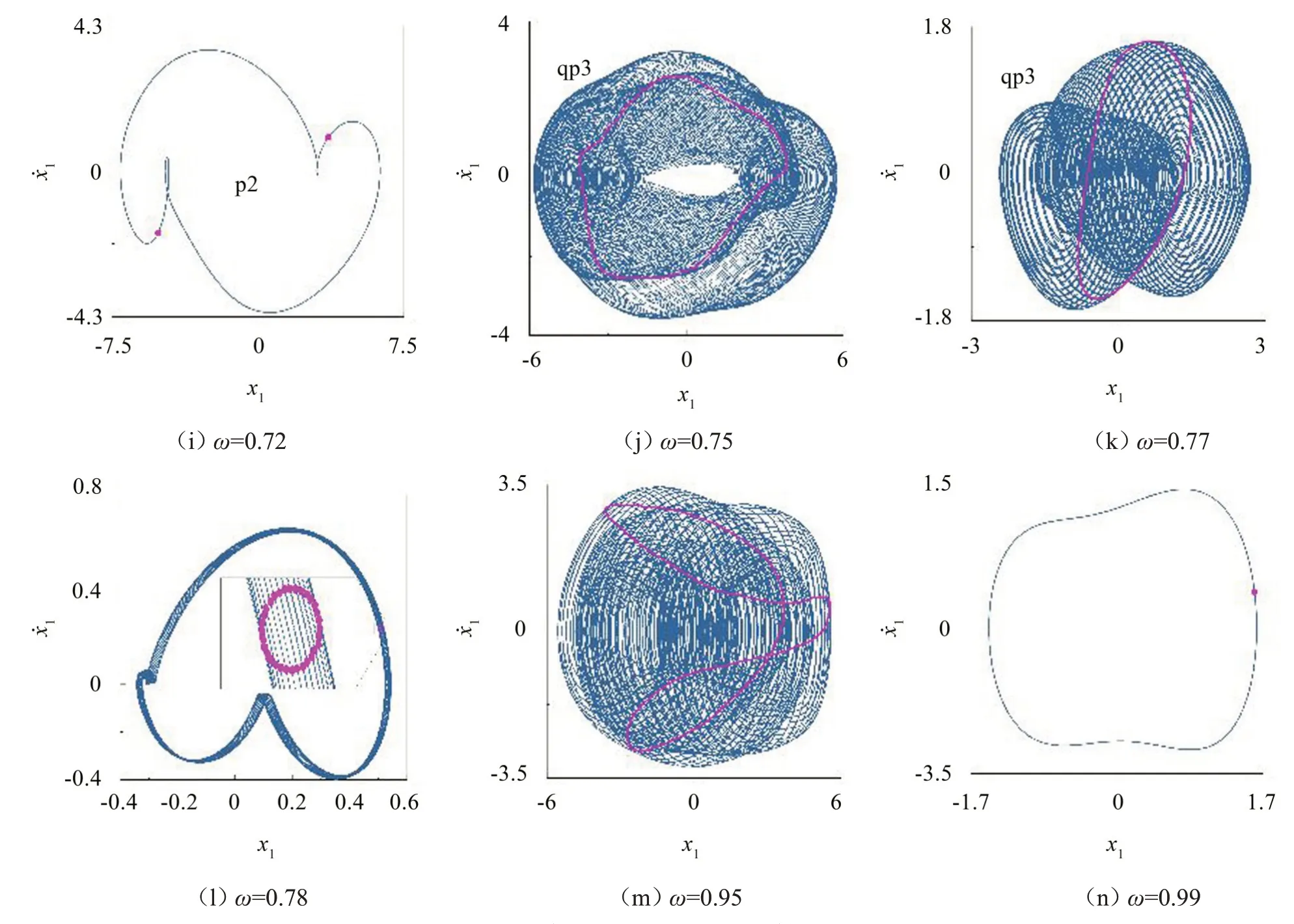
图6 系统相图和Poincaré映射图

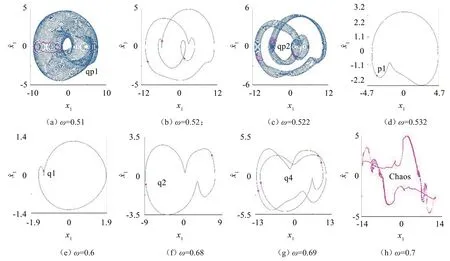
图6 系统相图和Poincaré映射图

可见，在不同外激励频率ω范围内，系统动力学行为不同，ω在0.5、0.7 和0.9 附近时，其动力学行为相对复杂，出现分岔和准周期行为，对应TLE值出现了大于0 和等于0 的情况。ω对系统振动的影响是间断性的，因此在实际应用中应选择合理的ω值，以避免不稳定和振动幅值较大的运动。

2.2 参数平面上系统非线性动态特性

图7指示外激励频率ω与减振块质量比m的关联作用对减振镗杆系统非线性动态特性的影响规律，图中每一个点（ω,m）的计算结果作为下一个点的初始值。图中不同颜色表示不同运动类型的存在区域，如周期1 运动p1（红色）、周期2 运动p2（黄色）、周期3运动p3（紫色）、周期4运动p4（品红色）、周期7运动p7（蓝色）以及非周期运动qp（天蓝色，可能是混沌运动或准周期运动）。

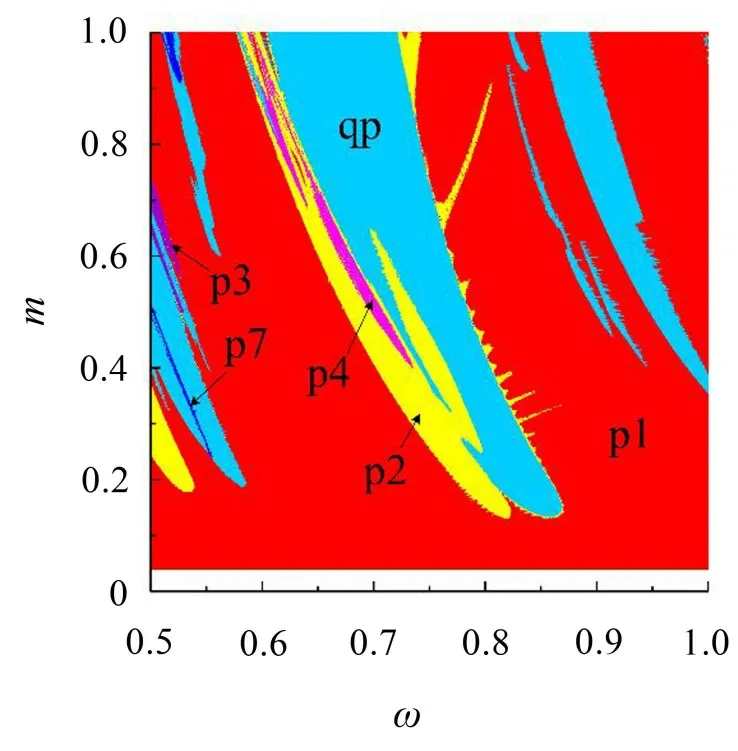
图7 ω-m平面上减振镗杆系统动力学行为分布特性

在参数平面ω-m上，系统在大部分区域内表现为稳定周期1运动p1，在较小区域内出现周期2运动p2 和周期4 运动p4，而在极小区域内出现周期3 运动p3和周期7运动p7。ω和m的组合关系对系统动力学行为的复杂性产生严重影响。如在ω=0.5 附近，m在0.2到0.7之间变化时，系统动力学行为相对较复杂，出现分岔、周期2、周期3、周期7 和非周期行为。

图3和图5分别为图7中ω=0.75和m=0.55时的两种特例。图3和图5与图7的一致性相对较好，图7能更全面地显示系统动力学特性与参数m和ω之间的关联关系和匹配规律，揭示参数关联下系统更多的动力学信息。

可见，ω与m的不同组合或匹配关系对系统非线性动态特性有重要的影响，在ω与m组合的大部分区域内系统运动较稳定，而在较小区域内系统运动较复杂，出现分岔和准周期行为，该区域内ω与m组合情况在工程应用中应尽可能避免。另外，参数相同时初值对系统动力学行为有重要影响，可能出现多稳态，这为后期进一步研究双参数与多初值关联下系统非线性动态特性提供方向。

2.3 系统非光滑特性

由于非线性阻尼力表达式（2）中符号函数(见式(3))的存在，随着减振块M2与杆体M1相对速度（-）的变化，系统可能发生切换现象，表现为非光滑行为。

便于分析和讨论，令m为参数变量，剩余参数与图3中一致，取状态边界条件（切换条件）为Poincaré映射截面，绘制镗杆杆体振动位移x1随m增大的分岔图如图8（a）所示，图8（b）为对应时间周期映射截面上减振块与杆体相对速度随m增大的变化规律。

对比图8（a）和图3，发现两图中除了P点到R点、S点到T点之间的区域，在m的其他范围内，系统动力学行为的分岔和演化过程基本一致。造成这一差异的原因是擦边分岔。图8（a）中在P点附近系统发生擦边分岔，对应相轨迹见图9（a），图中Z点附近系统轨迹与虚线相切，表示在Z点附近系统没有发生切换行为，红色符号“×”表示系统轨迹与切换面的交点，意味着切换现象发生。图中有2 个“×”，表示系统在切换面上表现为周期2行为。随m增大，在Z附近系统轨迹穿越切换面（或虚线=0），见图9（b），系统在切换截面上表现为周期3 行为，即有3 个“×”。表明随着m增大，在P点系统经擦边分岔由周期2行为转迁为周期3行为。

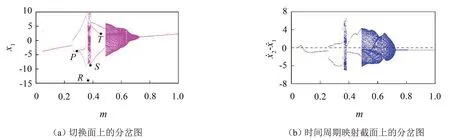
图8 m对系统非光滑特性的影响

随着m继续增大，在S点附近系统由混沌退化为周期3行为，对应相图见图9（c），相轨迹与切换面有3个交点（3个“×”）。在T点附近系统发生擦边分岔，由周期3 行为转迁为周期2 行为，相轨迹如图9（d）所示，其在M点附近与切换面（虚线）相切，且有2个“×”。

可见，擦边分岔会改变系统在切换映射截面上的动力学行为的类型，增加或减小系统运动轨迹与切换面的交点数量。由图9（b）可知，＜0均出现，表明系统切换现象确实发生。

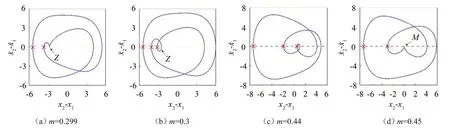
图9 擦边行为：（-, x2-x1）平面上系统相轨迹

3 减振质量块吸振能量特性分析

3.1 吸振能量模型

减振镗杆系统主要靠其内部质量块的振动吸收能量，从而减小镗杆振动。减振块振动能量Et主要包括动能Ek和由橡胶圈、阻尼液引起的势能Ep，可用式（6）计算得到。

式中，无量纲动能Ek和势能Ep可分别由式（7）和式（8）计算得到。

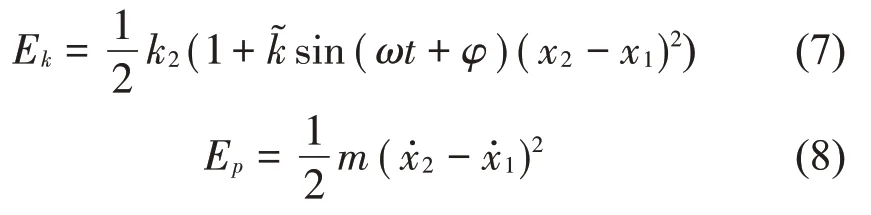
令Etmax、Ekmax和Epmax分别为时域内减振块吸收最大能量、最大动能和最大势能。

可见，减振块吸振能量不仅与其相对位移和速度有关，还与其质量、刚度、外激励频率密切相关。

3.2 吸振能量变化特性

为了与3.1 节对照分析，令镗杆质量为1，图10揭示减振块质量m对其无量纲最大吸振能量的影响。图中，减振块动能对其吸振能量贡献较大，而势能的贡献相对较小。在A点之前或F点之后吸振能量随m的增大呈增大趋势，且变化相对稳定，主要因为在此区域系统表现为稳定的周期1行为，m的大小对吸振能量的影响较大。在A和F点之间，吸振能量变化较大，其随m增大呈先增大后下降的趋势，主要原因是在A和F点之间系统出现分岔和准周期运动，系统动力学行为较复杂，见图3。可见，当系统运动较稳定时，吸振能量随m增大而增大；当系统运动相对复杂时，其吸振能量不仅与m有关，还与系统动力学行为密切相关。

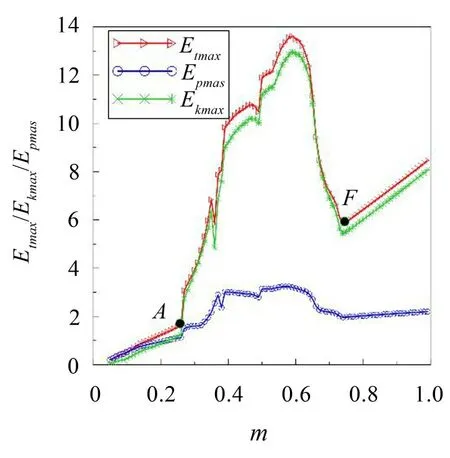
图10 减振块吸振能量随m的变化特性

图11描述外激励频率ω对减振块无量纲最大吸振能量的影响规律。减振块吸振能量主要由其动能Ekmax引起，在A和B点之间或G点之后，吸振能量变化相对稳定，且随ω的增大在G点之后呈增大趋势，在A和B之间呈减小趋势。在A点之前或B和G点之间，吸振能量变化相对复杂，主要原因是在该区域系统非线性动力学行为相对复杂，出现了分岔、混沌和准周期等，见图5。可见，当系统动力学行为相对稳定时，ω对减振块吸振能量的影响相对稳定，当系统动力学行为较复杂时，吸振能量与外激励频率ω和动力学行为均密切相关。

为分析减振块质量m和外激励频率ω关联作用对减振块无量纲最大吸振能量的影响规律，图12给出了两参数平面ω-m上减振块最大吸振量Etmax的分布特性。图10和图11为图12中当ω=0.75 和m=0.55时的两种特殊情况。在不同的ω和m关联或匹配下，减振块最大吸振能量相差较大，在Z1和Z2区域吸振能量较大，Z1区域最大吸振能量最高达到32，Z2区域最大吸振能量最高达23，其余区域最大吸振能量较小。

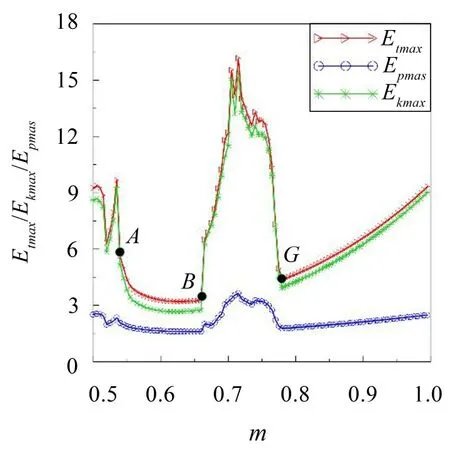
图11 减振块吸振能量随ω的变化特性

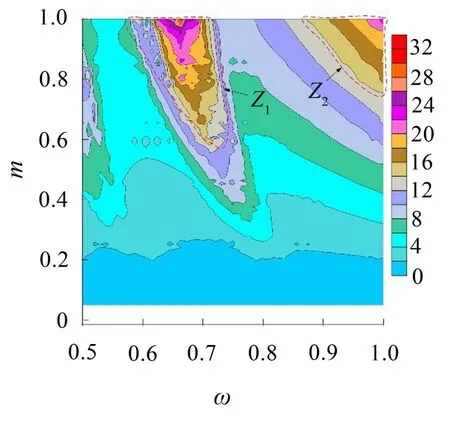
图12 ω-m参数平面上减振块无量纲最大吸振能量Etmax的分布特性

当减振块质量m较小时，减振块吸振能量较小，减振效果较差，且受外激励频率ω的影响很小。随着m的增大，吸振能量不断增大，且受ω的影响较大，如Z1和Z2区域。在Z1区域，在m和ω的关联下，系统出现分岔、混沌和准周期等非线性动力学行为，增加减振块吸振能量，但同时也加剧系统振动；在Z2区域，吸振能量同时随m和ω的增大而增大，系统吸振能量较大且表现为稳定的周期1 行为，减振效果最好。

可见，减振块质量m和外激励频率ω的关联协同作用对减振块吸振能量有重要的影响，在ω一定范围内，增大m有利于提升系统减振效果。

4 结语

本文考虑橡胶圈和阻尼液耦合作用下的非线性阻尼力和非线性弹性力，建立了两自由度减振镗杆系统非线性动力学模型，并通过减振块与镗杆杆体之间的相对运动分析，构建减振块吸振能量模型；基于建立的模型，研究了减振块质量和外激励频率及其关联协同作用对系统非线性动态特性和最大吸振能量变化特性的影响。具体结论如下：

（1）减振块质量比m和外激力频率ω对系统非线性振动影响较大。m在0.3 到0.7 之间取值，或ω在0.5、0.7 和0.9 附近取值时，系统动力学行为相对复杂，出现了分岔和混沌。一定参数条件下适当增加减振块质量或选择合理的外激励频率可以提升系统减振性能。根据ω-m平面上动力学行为的分布，可合理匹配减振块质量比和外激励频率以避免系统复杂或不稳定运动，提高系统稳定性。

（2）系统吸振能量主要由减振块动能构成，其势能的贡献较小。系统运动较稳定时，吸振能量随减振块质量比m增大而增大；出现分岔或混沌时，尽管吸振能量较大，但其动力学行为较复杂且不稳定。而外激力频率ω对减振块吸振能量的影响相对稳定；系统运动相对复杂时（如ω在0.5和0.7附近时），吸振能量不仅与减振块质量比m或外激力频率ω有关，还与系统动力学行为密切相关。通过合理匹配减振块质量和外激力频率的值，可以有效避免复杂运动，提高吸振能量，改善系统减振性能。本文的研究对减振镗杆系统参数优化设计、动态性能的改善具有一定参考价值。