陡坡段桥梁桩基研究现状及展望

赵明华，彭文哲，赵衡

（湖南大学土木工程学院，湖南长沙 410082）

川藏铁路、西部陆海新通道等“十四五”规划重点项目纳入国家战略，对我国中西部地区交通运输体系提出了新要求.自“一带一路”倡议提出以来，中西部山区高速公路、铁路建设迎来了新的发展阶段.作为一个多山的国家，我国山地面积约占国土总面积的2/3，新建桥梁占高速公路、铁路总里程的比重逐年攀升［1］.为满足山区交通线路的线形设计和生态保护要求，陡坡段桥梁桩基［2］与半路半桥设计形式被广泛应用于山区高速公路、铁路桥梁工程设计［3-4］，如成昆铁路、宝成铁路、张花高速公路和邵怀高速公路等.

陡坡段桥梁桩基承载机理及其设计计算方法与常规平地桩基及抗滑桩［5］存在显著差异［6-7］.在对陡坡段桥梁桩基进行受力变形分析时，不仅要考虑桥梁上部结构传递的竖向荷载［8-9］和车辆制动及强风甚至地震惯性力［10］等引起的水平荷载，还应考虑桩-坡非对称体系引起的桩后附加土压力［11］以及桩前地基水平抗力弱化效应［12］.

陡坡段桥梁桩基设计是我国高速公路、铁路建设向中西部山区延伸过程中所遇到的新课题.陡坡段桥梁桩基的桩-坡非对称体系导致桩前地基水平抗力及桩后附加土压力分布规律目前尚未探明，相关的桩-土相互作用机理也亟待探讨.因此，为保证山区高速公路、铁路桥梁桩基及其桥梁上部结构的安全，探究陡坡段桥梁桩基的承载机理，提出对应的设计计算方法，具有重要的理论意义与工程应用价值.

鉴于此，本文分别阐述了陡坡段桥梁桩基的竖向及水平承载特性和破坏机理；其次，分别介绍了相关的现场试验和模型试验方法；然后，进一步较为全面地总结了陡坡段桩基受力变形分析方法及其设计计算方法；最后，着重从施工技术、安全评价方法及加固处治措施等方面归纳了山区桥梁桩基施工要点及注意事项，以期为山区高速公路、铁路桥梁桩基设计及现行规范修订提供一些参考，相关成果也将产生一定的学术价值和社会经济效益.

1 承载机理研究

陡坡段桥梁桩基既要承受上部结构荷载，又要抵抗桩-坡非对称体系引起的桩侧附加土压力甚至滑坡推力；此外，临坡面土体缺失亦会引起桩前地基水平抗力弱化效应，故其承载机理和荷载传递机理极为复杂，与平地桩基存在明显差异.

1.1 竖向承载特性

陡坡段桥梁桩基的两侧土体呈现出非对称性，临坡侧土体缺失导致摩阻力难以充分发挥，从而引起桩基竖向承载力退化.许建聪课题组［13］依托某黄土地区桥梁桩基工程开展现场试验，总结出陡坡段基桩的竖向荷载传递规律具有较为显著的区域性：3 倍桩径深度范围内的临坡侧摩阻力发挥程度小于背坡侧，在3倍桩径至10倍桩径深度范围内，摩阻力发挥程度则反之，当深度大于10 倍桩径时，两侧的摩阻力发挥程度相近.冯忠居等［9］开展室内模型试验，获得了不同坡度和桩长条件下的基桩竖向承载力、桩身轴力及摩阻力等的变化规律：基桩竖向承载力及有效桩长均随坡度的增大而降低.Qu 等［14］采用三维有限元模拟分析了陡坡效应对均质土中竖向受荷群桩的影响，揭示了竖向荷载下群桩-土动力相互作用机制.由于双桩基础中连系梁对轴力的重分配效果并不明显，故在此并未区别讨论单、双桩基础的竖向承载特性.

1.2 水平承载特性

1.2.1 单桩基础

目前，国内外已有较多学者通过模型或现场试验，探究了陡坡段桥梁单桩的承载特性.湖南大学课题组针对我国中西部山区多条高速公路的陡坡段桥梁桩基设计及施工进行了长期的试验研究［7-8］，通过模型试验实测了不同组合荷载下的桩身弯矩及桩顶水平位移，并获得了桩侧土压力、地基水平抗力分布规律及陡坡效应影响范围［7］；近期，进一步分析了循环次数、荷载幅值及坡度等因素对陡坡段基桩水平循环响应的影响：桩顶水平位移随循环次数非线性增加，且其水平承载力与循环次数、荷载幅值及坡度均呈负相关［15］.此外，许锡昌课题组［16］基于模型试验，指出了基桩水平承载力随临坡距的增大而提高.赵其华课题组［17］基于现场试验，揭示了水平荷载下碎石土陡坡地基上的基桩变形、桩身弯矩及桩侧土压力的变化规律，并给出了不同坡度下基桩水平承载力折减系数的取值范围.尹平保等［18］进一步探究了空间效应对陡坡段基桩水平承载特性的影响，并依据模型试验实测结果，指出了陡坡段基桩水平承载力随水平荷载作用角度增加而提高.

此外，国外学者通过开展室内模型试验，总结出一些陡坡段桩基水平承载力受坡度和临坡距影响的一般规律.Muthukkumaran［19］分析了临坡距和砂土性质对陡坡段基桩水平承载特性的影响，并指出基桩水平承载力受边坡影响的临界临坡距应不大于15倍桩径，其结论仍过于保守.随后，Nimityongskul等［20］对比平地及边坡条件下的黏土p-y曲线，指出临界临坡距约为8 倍桩径.Rathod 等［21］基于软土边坡中铝管模型桩的水平静载试验，建立了不同坡度和长径比条件下陡坡段基桩水平承载力的多元回归方程，并指出基桩水平承载力受边坡影响的临界坡度约为11.30°.Raja和Muthukkumaran［22］分析出33.7°松散砂土边坡条件下的临界临坡距应大于5 倍桩径，并揭示了桩端嵌固条件对基桩水平承载力的强化效应.

1.2.2 双桩基础

山区高速公路、铁路桥梁行进方向多与边坡走向平行，前、后桩通过连系梁构成整体，与边坡形成独特的空间位置关系.其中，连系梁将在一定程度上约束前、后桩响应，并对桩顶倾斜荷载进行重分配；桩间土可将后桩的附加土压力按一定比例传递给前桩，故陡坡段桥梁双桩基础与常规单桩基础的水平承载特性存在显著差别.

鉴于此，湖南大学课题组通过室内模型试验，归纳出陡坡段双桩的桩-坡体系主要破坏模式及其影响范围［23］；并揭示了不同坡度下的双桩荷载传递规律及桩侧土压力分布规律［24-25］：受桩顶倾斜荷载及桩顶约束条件（弹性嵌固）的共同影响，双桩桩顶均存在负弯矩，其内力分布规律完全不同于双排门式抗滑桩［24］；临坡侧的摩阻力传递深度和反弯点位置均随坡度增加而下降，后桩附加土压力随深度先增大后减小［25］；进一步开展陡坡段桥梁双桩现场试验，揭示了不同工况下桩身轴力、摩阻力及桩身弯矩分布规律：竖向荷载全部由摩阻力承担，上部土层与下部岩层提供的摩阻力之比随竖向荷载增大而减小，且前、后桩桩顶均存在负弯矩［8］.

1.3 破坏机理

如前所述，陡坡段桥梁桩基不仅要承受桩顶倾斜荷载作用，还要承受由坡面和坡顶堆载以及桩-坡非对称体系形成的侧向附加土压力，其破坏机理也将完全不同于平地桩基.一方面，桩侧阻力和桩端阻力可能不足以承担竖向荷载，导致土体剪切破坏，进而引起桩基失稳破坏；另一方面，桩侧土体或许难以提供足够的地基水平抗力，导致土体屈服破坏，从而引起桩基结构功能失效.

然而，考虑到陡坡段桥梁桩基的埋深通常比较大，且现行规范［3-4］规定桩端必须嵌入稳定岩层，故其破坏模式多为桩基水平变形过大而难以满足上部结构要求（包括桩身材料弯曲或受拉破坏）、桩前土体屈服甚至桩-坡体系发生失稳破坏等.陡坡段桩基施工过程中，受施工机械扰动等影响，边坡的原有平衡状态极易受到破坏，进而发生变形甚至滑移，且上部结构荷载引起的桩身变形也会影响桩前坡体的稳定性，最终引发整个桩-坡体系的完全失稳.

针对其破坏机理，国内外一些学者已开展了较多的研究.湖南大学课题组基于现场及模型试验，总结出陡坡段桥梁双桩破坏模式主要为桩基水平变形过大且坡体发生水平侧移等.在复杂荷载作用下，桩前2～5 倍桩径深度范围内出现明显的“八”字形或“剪刀”形裂缝，且开裂区域宽度和长度随荷载增加而增大，最终导致边坡整体失稳破坏［23］.随后开展的单桩模型试验也揭示了陡坡段桩基主要破坏模式为桩周土体拉裂破坏：桩前土体出现明显隆起及裂缝，并与桩身成一定角度向前延伸，随着荷载继续增大，裂缝数增加且延伸至坡面，桩身位移随之增大［26］.桩前土体破坏区域主要集中在桩前一定宽度范围内，根据裂缝形态，可将其视为破坏楔体，即桩前土体受压进入塑性状态，最终呈楔体破坏［27］.国外学者Gabr和Borden［28］对平地水平受荷桩破坏模式进行改进，考虑边坡的存在对近地表处破坏楔体的影响，将其破坏模式推广至陡坡地基.相似地，Nakasima等［29］和Uto等［30］在分析大直径桩的桩前坡体局部稳定性时，分别对破坏楔体的几何形状作出了一些假定.上述研究对陡坡段刚性桩破坏机理进行了初步探讨，但其研究成果难以适用于柔性桩.为此，Ng 和Zhang［31-32］借助有限差分软件揭示其桩周土体的塑性区发展规律：桩侧剪切塑性区随着荷载增大而逐渐拓宽、拓深，水平荷载通过基桩向更深处土体传递，形成广泛的桩侧楔形塑性区，进而引起桩前楔体的局部破坏甚至整体破坏.随后，模型试验和有限元数值结果［33］显示除桩前土体外，刚性桩桩后和桩端也会形成破坏区域，同时受临坡距和水平荷载控制；临坡距较大时，破坏面仍在坡顶范围内，随着临坡距逐渐减小，破坏面将越过坡顶边界向坡面延伸［33］，上述现象与模型试验［19］及全尺寸试验［20］现象吻合较好.陡坡段基桩全尺寸试验［20］中，桩前和桩后均形成裂隙（垂直于加载方向以及与加载方向成45°），近地表土体出现楔形破坏［27］，而对于平地桩基，主要为向上移动和膨胀而产生明显的隆起现象.综上可知，楔形破坏模式已被较多学者接受，但其几何形状（如剪切破坏角）以及楔体侧面是否提供阻力尚无统一的观点［28］.Gabr 和Borden［28］认为黏性土剪切破坏角为φ/2，松砂剪切破坏角为φ/3～φ/2，密砂剪切破坏角约为φ.亦有学者通过模型试验，提出了剪切破坏角约为0.75φ或φ/2，且与荷载及基桩位移有关；或者破坏楔体的剪切破坏角随临坡距的减小而增大，并建议剪切破坏角取0.7φ.

2 现场及模型试验方法研究

2.1 现场试验方法

目前尚无专门针对陡坡段桥梁桩基现场试验方法的相关规范，故现场试验仍需借鉴平地桥梁桩基相关规范，相关试验装置及试验流程详见《公路桥涵地基与基础设计规范》（JTG 3363—2019）［3］和《铁路桥涵地基和基础设计规范》（TB 10093—2017）［4］，不在此赘述.

目前，相关学者一般根据现场勘探试验（包括钻孔试验、SPT 和CPT、DMT 等）［20］及原状土的室内土工试验，揭示试桩处地层分布及其主要的物理力学性质.此外，沿桩轴线自地面以下每隔一定距离在钢筋笼上安装一对钢弦式钢筋应力计（沿边坡倾向对称）和电阻式钢筋应变计（沿边坡走向对称），并在桩端埋设土压力盒，以测量试桩内力发展规律.为直接监测试桩的变形和偏转情况，可沿桩安装一系列位移计和测斜仪，由于试桩在近地表处的位移变化较大，故此处应变计较多.若有条件开展水平静载荷试验，则可通过伺服油压/液压千斤顶等施加拟静力水平荷载，并通过测力元件等控制静载水平.若试桩处难以实施静载试验，可结合桥梁施工进度，采集桥梁在上、下部结构自重及成桥后车辆加载等工况下的桩身内力发展规律［8］.

2.2 模型试验方法

2.1.1 相似准则

相似第二定理给出了相似准则的推导方法：定律分析法、量纲分析法和方程分析法.从理论上来说，三种方法均可推导出相同的相似准则，仅仅是用不同方法对相似现象做数学上的表述.

在倾斜荷载下基桩挠曲微分方程式（1）的基础上，采用方程分析法可推导出陡坡段桥梁桩基的相似准则，见式（2）和式（3）.

式中：EpIp为基桩抗弯刚度；y为基桩水平位移；z为深度；P为竖向荷载；b0为基桩计算宽度；m为地基反力系数的比例系数；λm、λb、λz和λEI分别为地基反力系数的比例系数m、基桩计算宽度b0、埋深z和基桩抗弯刚度EpIp的相似比.

2.1.2 模型边坡填筑

模型试验通常在试验箱或试验槽中进行，其尺寸设计应考虑模型桩尺寸及桩基作用影响范围：10倍桩径或者荷载方向上8～12 倍桩径和垂直于荷载方向上3～4 倍桩径［22］.试验箱通常为钢板与有机玻璃的组合结构，四周由型钢固定，可通过横向加筋肋增强其整体抗弯能力，透明玻璃面可便于直接观测桩-坡体系变形及破坏现象.在同时开展多组模型试验时，可采用固定木质分隔板隔离，防止各组模型试验之间相互影响［24］.

当模型边坡填土为砂土时，应在模型试验前，对其进行一系列物理力学试验，获得其物理力学指标（如重度、含水率、弹性模量、孔隙比、内摩擦角、曲率系数和不均匀系数等）.若为河砂，则应晾晒后过筛，去除颗粒杂物，才可通过颗粒筛分试验得到其级配曲线.为忽略模型土的尺寸效应，模型桩桩径与粒径d50（小于该粒径的土粒质量占土的总质量的50%的粒径）的比值应大于40［34］.为确保模型边坡的填砂密度接近（密实度可通过砂土的自由落体高度控制），常采用砂雨法进行填筑［34］，通过漏斗产生均质砂土水平地面，进而进行开挖削坡处理，形成不同坡角和高度的砂土边坡.在采用砂雨法进行填筑期间，可通过圆锥静力触探法，记录土体不同填筑深度时的CPT曲线，以证实砂雨法重建土体后的均匀性.

当模型边坡填土为黏性土时，也应在模型试验前，对其进行一系列物理力学试验，获得其物理力学指标（如黏聚力、内摩擦角、液限、塑限、最优含水率、最大干密度、压实度和弹性模量等）.在填筑边坡之前，可在试验箱内壁贴上塑料薄膜并涂上润滑油，以减小试验箱（槽）侧壁摩擦的影响.为保证模型边坡填土密实均匀，可预先在试验箱每隔一定深度进行标记，进而分层夯实（或振动密实）填筑.在逐层填筑过程中，每次填土量应相同，控制好干密度范围，并将每层土夯实至相应标记处，每层夯实次数相同，以保证土样均匀密实，均匀夯实后再填筑下一层，填筑到设计标高后统一刷坡到预定坡度，再静置7 d以保证边坡稳定性.若边坡存在滑动面，可采用塑料薄膜模拟［7］.为检验黏土层的均匀性，可从不同深度采集黏土样品，测定其重度和含水率，保证二者仅在较小范围内变化.

2.1.3 模型桩制作

常见的模型桩主要有铝管、钢管、ABS 塑料管、聚氯乙烯（PVC）管、三型聚丙烯（PPR）管，其外径（三截面交叉法）和壁厚、桩长和埋深可以根据相似准则和抗弯刚度（简支梁法或悬臂梁法）等确定.在此基础上，通过相对刚度因子Kr、刚度系数T或桩的水平变形系数α［3］，可将基桩划分为刚性桩（Kr＞10-1、Lem＜2T、αLem≤2.5）或柔性桩（Kr＜10-2、Lem＞4T、αLem＞2.5）.

式中：Es为埋置深度范围内土体加权平均割线模量；Lem为埋置深度；nh为地基水平反力系数.

成桩可采用钻孔灌注、打入或预埋等方式.对于预埋桩，为模拟桩土接触，保证桩身具有一定粗糙度，可在桩身涂抹少量胶水，使其均匀附着一定厚度的细砂.将模型桩从预留孔洞中插入固定后，可用经纬仪监测桩身是否铅直.如有必要，可在桩身上布置金属圆环［16］，以便后续施加水平荷载.可根据对应的工程实际选择桩顶和桩端边界条件（嵌固或自由）.为模拟桩端嵌固条件，可采用水泥、石膏和砂的混合料或者混凝土、钢筒等进行固定.

2.1.4 测量元件及其系统

加载过程中地表处桩身所产生的水平位移及转角，可通过在桩顶处布设LWH 拉杆式直线位移传感器或LVDT 线性可变差动变压器、光电位移传感器、百分表或千分表等测定.在模型桩预埋之前，可在桩端及沿桩身一定间隔放置土压力盒，以测定每级荷载稳定后的桩侧土压力分布规律以及桩端阻力.为测定桩身应变及弯矩，可沿桩长每隔一定距离对称布置一对电阻式应变片（1/4 桥、半桥、全桥法），并以AB 胶或硅胶封存保护，以避免应变片与土体直接接触.为尽量减小应变片接线对实测结果的影响，接线从桩侧面打孔穿过，自桩顶引出.试验前应对应变片进行平衡操作以及应变归零，并检查应变片是否处于正常工作状态.应变片数据均由静态电阻应变采集仪和计算机系统采集，各测点弯矩可据式（7）或式（8）计算.

式中：εc和εt分别为压应变和拉应变；D为桩径；ε为微应变；C为校准常数.

桩身弯矩曲线可采用局部五次样条函数、三次或六次多项式等函数拟合，通过对其进行二次微分即可交叉验证应变片和土压力盒的测量结果.在拟合和微分过程中，无须引入额外的条件或假设（如地表处或桩端处土压力为零）.为提高土压力分布曲线的精度，应在桩顶和桩端处适当增加测量点的数量.

2.1.5 荷载施加

水平荷载可通过多种方式进行施加，如伺服油压/液压千斤顶、作动器、电机、自制无摩擦定滑轮装置、多通道协调加载试验系统等，加载速度或幅值可由压力传感器和计算机系统控制操作.采用慢速维持荷载法进行逐级加载，每级荷载增量通过预试验确定，约为预估水平极限承载力的1/15～1/10，模型桩容许水平承载力取桩顶位移为0.2 倍桩径对应的荷载.然后，按0、5 min、15 min、30 min、1 h 的时间间隔分别获取传感器数据，当地表处水平位移的变化速率小于0.01 mm/（1～5）min 且累计小于0.1 mm/h时，方可施加下一级荷载.若在某级荷载下，当桩身出现断裂、地表处位移急剧增加、地基土出现明显贯穿裂缝或隆起时，视为极限承载状态，应终止加载并逐级卸载至零.

竖向加载可采用机械式自平衡重物加载装置，通过球铰架设于模型桩桩顶，能随桩顶移动并自行调整平衡，以保证施加荷载为竖向力，不产生水平分力.竖向荷载亦采用慢速维持荷载法进行逐级加载，当某级荷载下桩顶沉降量小于0.1 mm/h 时，则认为已达稳定，然后再施加下一级荷载，当某级荷载下的桩顶沉降量大于前一级荷载沉降量的5 倍时，则终止加载.

此外，在坡体平台上堆载使坡体对模型桩产生水平推力，可模拟施工阶段中桩基上方边坡的施工便道和重型施工设备.

试验加载过程中需要测定桩顶水平位移、桩身应变和桩侧土压力.在施加第一级荷载之前，首先检测各测量元件，确认各测量元件性能良好，并做好加载前初读数的采集工作.每级荷载施加后，恒载5 min测读桩顶水平位移，并同时采集应变和土压力数据.

3 受力变形分析及其设计计算方法研究

3.1 考虑竖向摩阻力弱化的竖向承载力计算方法

常规平地桥梁桩基竖向承载力可通过静载荷试验、经验公式法、动测法和沉降计算方法（弹性理论法、荷载传递法和剪切位移法）等方法确定.然而，由于陡坡段桥梁桩基的桩侧土体存在非对称性，导致临坡侧约束及摩阻力难以充分发挥，故其竖向承载力明显低于常规平地桩基，若直接采用现行规范或文献方法进行设计计算，则偏于不安全［35］.

为此，牛富生等［13］基于现场试验，考虑桩-坡非对称性对基桩竖向承载力的折减效应，提出了相应的修正计算公式.尹平保等［36］假定浅层区域地基抗力呈非线性分布，建立了基桩稳定性分析简化模型及桩-坡体系总势能方程，进而提出了基于能量法的陡坡段基桩屈曲荷载及桩长设计方法.随后，进一步开展模型试验，推导出考虑坡度及桩长影响的陡坡段基桩屈曲荷载理论计算公式［37］.

3.2 考虑极限地基水平抗力弱化的水平承载力计算方法

桥梁桩基以承受竖向荷载为主，但在车辆制动荷载、风荷载甚至地震荷载等作用下，也将承受一定的水平荷载，故其工程设计不仅要满足竖向承载力要求，还须验算水平承载力，且研究及实践表明，单桩水平承载力远低于其竖向承载力.然而，由于陡坡段桥梁桩基的桩侧土体存在非对称性，导致临坡侧极限地基水平抗力难以充分发挥，故其水平承载力明显低于常规平地桩基.

许锡昌课题组［16］结合模型试验及数值模拟，提出了可考虑坡度和临坡距的陡坡段基桩水平承载力简化计算方法.Chae 等［33］以原型和模型试验为依据，运用三维弹塑性有限元法，分析了砂土边坡对桩前地基水平抗力的弱化效应.蔺鹏臻等［38］采用ANSYS有限元软件模拟某黄土边坡上铁路桥梁桩基工程，分析出受水平地震和边坡推力综合影响，临坡侧的基桩竖向位移和正应力远高于背坡侧应力.Zhang等［39］开展三维数值分析，探究了坡度和套管厚度对基桩水平承载特性的影响，建立了陡坡段基桩与平地基桩响应的经验关系.

此外，一些学者开始采用极限地基反力法，推导陡坡段刚性桩水平承载力理论解.Gabr 和Borden［28］通过建立静力平衡模型，分别推导出以坡度和土体强度为参数的砂土和c-φ土陡坡地基中刚性桩水平承载力理论解.湖南大学课题组提出陡坡地基桩前土体的极限破坏模式，并基于极限分析上限定理，推导出刚性桩水平承载力计算方法及其简化拟合公式［40］；在此基础上，假定桩前土体非对称破坏模式，引入强度发挥系数考虑旋转中心以下土体抗剪强度的影响，结合极限分析上限定理和静力平衡条件，推导出陡坡段刚性桩水平承载力解析解，进而引入有效埋深概念，将其成果推广至柔性长桩［41］.Georgiadis 等［42］基于静力平衡条件，推导出考虑桩-土界面黏聚力的不排水条件下黏土中刚性桩水平承载力表达式，并给出了水平承载力与坡度、临坡距、长径比、荷载偏心率以及桩-土界面黏聚力相关的设计图表.Jiang 等［43］和Liu 等［44］假定桩侧极限地基抗力及其模量的表达式，并基于静力平衡条件，分别提出了在砂土边坡和黏土边坡上的水平受荷刚性桩非线性分析方法.

3.3 m值和p-y曲线弱化效应

3.3.1m值弱化

如前所述，陡坡段桩基两侧岩土体的非对称性将导致地基水平抗力弱化，可表现为地基反力系数的比例系数m值弱化，但陡坡条件下m值取值至今尚无明确规定［3-4］.因而，在缺乏充分资料且难以对m取值作出统一规定时，陡坡段桥梁桩基设计人员被迫结合经验，忽略或弱化一定深度范围内的地基水平抗力.

湖南大学课题组基于一系列模型及现场试验成果［7-8，15，23-25］，建议将陡坡效应影响深度范围内m值取为平地m值的一半.随后，尹平保等［18］通过室内模型试验，指出陡坡条件下m值随地表处桩身位移、坡度及水平荷载作用角度增加呈非线性减小，并建立了相应的拟合关系式.此外，针对我国西南地区典型碎石土陡坡地基的m值取值问题，赵其华课题组［45-46］也作出了较多的研究工作：基于水平静载试验，提出了以平地m值为基础的碎石土陡坡地基m值修正公式及其取值范围［45］；在此基础上，结合现场试验、模型试验及数值模拟，进一步提出了考虑坡度、土体密实度、桩长及桩径的碎石土和碎石土-基岩陡坡地基m值的估算公式及其修正系数［46］.

3.3.2p-y曲线弱化

现行规范中p-y曲线主要源于平地条件下的原位试验和室内试验，在分析陡坡地基问题时存在局限性.

为此，一些学者试图通过陡坡段水平受荷桩室内模型试验，探明陡坡效应引起的地基水平抗力弱化规律.年廷凯等［47］深入分析桩侧地基抗力与桩身位移的分布规律，提出了适用于粉土边坡的简化p-y曲线表达式.随后，通过对桩侧土体极限抗力和初始刚度的合理修正，张陈蓉课题组［48］推导出砂土边坡浅层区域的双曲线型p-y曲线表达式；杨明辉等［49］提出了黏土边坡浅层区域的p-y曲线表达式以及陡坡效应影响深度与坡度的经验关系，并量化了陡坡段基桩水平承载力折减程度与坡度和临坡距的关系.此外，尹平保等［6］对Matlock 黏土p-y曲线及双曲线型砂土p-y曲线进行修正，分别构造了黏土和砂土边坡的p-y曲线.

国外学者亦基于现场或模型试验结果，引入折减系数考虑陡坡效应，对平地p-y曲线进行修正.Mezazigh 和Levacher［34］采用局部五次样条函数拟合离心模型试验实测弯矩曲线，提出了陡坡条件下的干砂p-y曲线修正系数.Muthukkumaran 等［50］采用三次多项式拟合模型试验实测弯矩曲线，引入折减系数对API RP 2A 方法进行修正，建立了超载作用下的砂土陡坡地基无量纲p-y曲线.K.Georgiadis 和M.Georgiadis［51-52］采用三维有限元方法，提出了考虑不排水抗剪强度、坡度和桩-土界面黏聚力的新p-y准则［51］；在此基础上，进一步考虑地基水平抗力分布随临坡距的演化规律，提出了考虑临坡距的p-y曲线表达式［52］.Nimityongskul 等［20］对平地及边坡条件下的黏土p-y曲线进行归一化处理，提出了考虑陡坡效应的p-y曲线p乘子.Chen 等［53］假定水平受荷桩将桩前土体压缩成土楔体，并考虑陡坡效应对双曲线型p-y曲线的影响，提出了基于楔体平衡分析的砂土边坡极限地基水平抗力计算方法.与此同时，Liu 等［54］进一步考虑临坡距对p-y曲线的影响，提出了基于楔体平衡分析的黏土边坡极限地基水平抗力计算方法.

3.4 倾斜荷载下陡坡段桥梁桩基设计计算方法

陡坡段桥梁桩基不仅要承受桥梁上部结构及载具自重导致的竖向荷载，还要承担车辆制动和强风甚至地震惯性力等造成的水平荷载，同时受到桩-坡非对称体系引起的桩后附加土压力，故其挠曲微分方程应为：

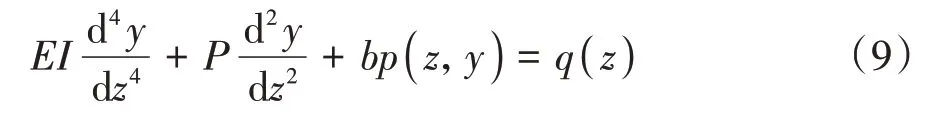
考虑到地基水平抗力p（z，y）的确定方法不同，可将当前陡坡段桥梁桩基设计计算方法主要分为弹性地基反力法和复合地基反力法（p-y曲线法）.

3.4.1 弹性地基反力法

该方法假定地基土为服从胡克定律的弹性体，地基水平抗力p（z，y）的表达式为

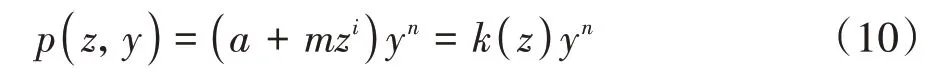
式中：a、i、m、n均为待定系数，n取决于桩身水平位移，且根据n的取值可将弹性地基反力法分为非线性弹性地基反力法和线弹性地基反力法.

1）非线性弹性地基反力法（n≠1）.

当桩基水平位移较大时，桩侧土体变形将不再是线弹性的.最具有代表性的是日本港研法，包括林-宫岛法和久保法.但由于此法很难给出非线性微分方程的解析解或近似解，过于复杂的计算过程限制了其在工程设计中的应用.

2）线弹性地基反力法（n=1）.

根据Winkler 假定，此法将桩周土视为离散弹簧，并忽略其连续性；一般通过指定k（z）中的两个参数，简化地基水平抗力的计算，获得常数法（张氏法）、k法、c法和m法等常用方法.其中，张氏法假定m=0，即k（z）为常数，与深度无关，故其数学处理最为简单；m法假定i=1，即k（z）=mz，运用该方法精确求解基本微分方程难度颇大，故往往需要借助一些数学近似手段，并作出简化计算图表以便查用.

综上可知，线弹性地基反力法未能考虑地基土的连续性，且将桩身任一点的地基抗力和水平位移视为线性相关，难以精确反映土体复杂性质，故其仅适用于小荷载和小位移条件.然而，恰好公路、铁路桥梁桩基一般不允许地面处水平位移过大（6～10 mm），故我国公路、铁路桥涵地基与基础设计规范［3-4］依然沿用线弹性地基反力法，并给出了不同类别土的m值取值范围，指出当桩基在地面处位移超过容许值时，应适当降低.

基于弹性地基反力法，湖南大学课题组多年来针对陡坡段桥梁桩基设计计算理论作出了大量研究工作［15，55-60］.初期，根据现场实测数据，假定桩后附加土压力呈两端小中间大的抛物线型分布，且桩前地基反力系数服从m法假定，推导出考虑P-Δ效应的倾斜荷载下陡坡段基桩内力变形有限差分解答［55-57］及幂级数解答［58］；随后，基于极限平衡理论推导了桩后附加土压力的计算公式，并采用幂级数法求解挠曲微分方程，提出了陡坡段桩柱式桥墩基础设计计算方法［59］；综合考虑P-Δ效应及桩土共同作用的影响，对传统有限杆单元法中单元刚度矩阵进行修正，提出了适用于陡坡段基桩内力变形分析的改进有限杆单元法［60］.近期，通过室内模型试验，以水平静载下桩顶水平位移为基础，分析出可考虑坡度、水平荷载幅值及循环次数影响的陡坡段水平循环受荷桩的桩顶水平位移拟合公式［15］.此外，蔺鹏臻等［38］基于有限差分法提出了考虑滑坡推力和地基抗力折减的基桩内力变形计算方法.董捷等［61］考虑桩前三维楔形体的受力平衡条件及临界稳定状态，提出了陡坡段基桩自由段长度的设计计算方法.杨果林课题组［62］基于三参数地基模型，建立了考虑竖向摩阻力的挠曲微分方程，并采用传递矩阵法结合Laplace变换公式，推导出陡坡段基桩挠曲半解析解.

上述设计计算方法均针对陡坡段桥梁单桩，难以考虑桥梁双桩基础的复杂受力变形特性.为此，湖南大学课题组借鉴深基坑护坡桩的土压力理论，合理简化桩后附加土压力，提出了基于幂级数法的桥梁双桩基础内力变形计算方法［63］；并对传统有限杆单元法进行修正，提出了考虑P-Δ效应与桩土共同作用的陡坡段双桩设计方法［64］.近期，通过桩顶变形协调条件考虑连系梁的影响，并引入土压力理论考虑桩间土的作用，推导了陡坡段双桩内力变形有限差分解答［65］；进而分别引入应变楔理论和弹性地基反力法分析陡坡段双桩基础桩侧土压力，并考虑PΔ效应、桩土共同作用和土体剪切作用，对有限杆单元法中单元刚度矩阵进行修正，提出了复杂荷载下陡坡段桥梁双桩基础受力变形分析方法［66］.此外，张永杰等［67-68］提出了基于结构位移法的陡坡群桩基础分析方法及优化设计方法［67］；进而针对桥梁双桩基础承载特性，建立了相应的简化分析模型，并基于桩侧受均布力假定，提出了陡坡段双桩基础简化设计计算方法［68］.

3.4.2 复合地基反力法

该方法认为水平受荷桩的桩侧土一定深度以上为塑性区（极限地基反力法），此深度以下为弹性区（弹性地基反力法），也称弹塑性分析法.作为应用较广的一种方法，p-y曲线法沿深度方向将桩侧土应力-应变关系用一组曲线来表示，即在某一深度处，建立桩基水平位移与单位长度地基反力合力之间的对应关系.此法可考虑桩侧土与柔性长桩水平变形的非线性关系，在分析较大变形问题时，比弹性地基反力法更为优越，已被港工规范及固定式海上平台规范广泛接受.

湖南大学课题组深入分析陡坡段桥梁桩基的承载特性和荷载传递机制，采用p-y曲线考虑桩土相互作用，获得了考虑桩体自重和竖向摩阻力等影响的陡坡段基桩内力变形有限差分解［69］；结合桩侧摩阻力和桩后附加土压力的分布规律，获得了对应的等效结点荷载向量表达式，并引入p-y曲线对地基水平抗力进行非线性分析，进而基于考虑P-Δ效应的修正有限杆单元法，提出了陡坡段基桩内力变形计算方法［70］.近期，对平地应变楔模型进行修正［71］，考虑陡坡效应对应变楔应力-应变关系的影响，提出了坡顶处水平受荷桩内力变形计算方法［12］；并进一步引入土楔理论考虑桩后附加土压力，将其计算方法推广至陡坡任意位置处基桩［11］.近期，基于小比例模型试验，提出了考虑坡度及临坡距影响的修正应变楔模型及对应的p-y曲线［26］；通过基桩挠曲微分方程迭代求解应变楔深度及应变，获得了陡坡段基桩内力变形非线性分析的有限杆单元解答［27］.

4 施工技术和安全评价方法及加固处治措施研究

4.1 施工技术

陡坡段桥梁桩基的施工受到山区复杂地形地貌特征和水文地质条件限制（地形高差较大、沟谷纵横、稳定性差、交通不便等）.若盲目照搬平地桥梁桩基的施工工艺和管理措施，或将导致工作面的过度开挖，造成周边岩土体环境及天然排水系统破坏，进而引发岩土体失稳和滑塌等工程病害，严重影响工程进度，造成经济损失.在实际施工过程中，由于陡坡段桥梁桩基设计处于初期阶段，缺乏必要的施工标准和管理措施，甚至没有相对可靠、健全的安全防护技术，难以满足施工要求.鉴于此，国内外一些学者结合山区桩基施工难点及工程经验，总结出一些陡坡段桥梁桩基标准化施工工艺，以期保证施工质量及施工的有序进行.

4.1.1 成孔工艺

因机械设备在山区运输和安装困难，成孔泥浆和废渣难以排出，不利于生态保护，施工难度较大，故常采用人工挖孔方式.在桩基成孔时，应在施工现场围建适当的护壁并加固井口围栏，可避免坡面上的岩石及杂物落入，并有效阻断坡面水流入孔内.在上覆土层挖孔施工时，应在孔位处采用1 m 左右的支护架，采用细石混凝土作为护壁基础性材料，整体厚度为15 cm 左右，每节桩孔挖完后，应用竹竿在上下左右水平转动，以保证桩孔质量.若无法打进或打进速度较慢，难以满足工期要求，则可根据工程实际，按照既定管理体系，在保证孔壁基本稳定性和周边环境安全的同时，采用毫秒微差的爆破技术均匀击碎岩石.

此外，在山区桥梁桩基施工时，若采用混凝土护壁，应将护壁从孔口处地面以上10～30 cm 一直延伸至风化层底部.护壁混凝土结构采用双层钢筋布置形式，网格间距约为20 cm，钢筋网及锚头采用电焊连接.同时，应将水平钢筋伸出模板10～15 cm，以便其与其他钢筋有序连接.桩孔进入岩层后，应在临空侧护壁上采用钢筋混凝土进行加固，锚杆安装过程中要保证操作程序的稳定性，首先注浆，其次安装钢筋网，最终浇筑.

4.1.2 成桩工艺

钢筋笼在山区桥梁桩基标准化施工中起着重要作用.为保证钢筋笼顺利制作下放，在交通不便、机械设备难以到达孔位处时，可在孔位的施工平台完成制作后直接下放.此外，可采用吊车沉放，在距桩孔10 m 处设置吊线，必要时对钢筋笼进行垂直控制，将其悬于钢筋笼轴线上，并避免出现钢筋笼摇晃现象.

在山区桥梁桩基浇筑过程中，由于缺少地下水，大多采用干灌法，且应将混凝土搅拌均匀，尽量缩短运输距离，减少颠簸.浇筑过程必须连续，避免出现导管进水导致断桩的情况.由于灌注桩桩顶高于常规设计高度，应将设计高度以上的浮浆和混凝土及时消除，以保证施工质量.

4.1.3 质量管理措施

加强施工现场管理是加快工程进度、保证工程质量及安全的关键因素，应合理设置安全警示牌，对工程地质情况、施工方案及工程进度进行透明化管理，负责人则要明确自身责任意识，明确分工，进而提升标准化施工质量.山区桥梁桩基施工过程中，应建立完善的组织结构，对施工人员进行安全教育，按照既定的管理制度，确定安全管理原则，并在执行阶段，对各施工程序及桩基施工要点进行严格审核.若存在审核不到位或制度不严谨的情况，则应将责任落实到个人，进而保证管理体系的有效性.

4.2 安全评价方法

桥梁桩基边坡稳定性评价是山区公路、铁路工程常见的复杂技术难题.桥梁上部结构荷载及桩体自重等附加荷载通过桩基础向岩土体边坡传递侧向应力，提升了滑坡风险.由于附加荷载下桥梁桩基边坡稳定性分析较复杂，相应的分析方法尚不成熟，陡坡段桥梁桩基工程的质量和安全难以得到有效保障.为此，有必要提出和完善桥梁桩基边坡的安全评价方法［3-4］，以保证山区桥梁桩基安全施工以及桩-坡系统的整体稳定性.

目前，桥梁桩基岩质边坡的稳定性分析方法主要有：1）稳定坡角法.根据岩质边坡几何形态及其水文地质条件等，分析出天然状态下边坡的稳定坡度线，桥梁桩基须嵌入此坡度线以下.从既有设计合理的稳定边坡中，通过统计分析获得稳定坡角与边坡各参数之间的关系，拟合出基于岩体质量或基于SMR的经验公式.2）应力分析法.桩-坡非对称性使得临坡侧一定区域内出现应力松弛带，通过对比不同应力松弛带，并考虑施工难度，即可确定桥梁桩基的最佳位置.

显然，各行业规范及手册并未给出桥梁桩基边坡稳定性分析方法，相关研究也鲜有报道.Uto 等［30］报道了两例水平受荷桩引起砂土和软岩边坡失稳的工程实例.Nakasima等［29］假定桩前破坏楔几何形状，提出了陡坡段水平受荷桩所在边坡的局部稳定性分析方法.Ng 和Zhang 等［31-32］通过三维有限元分析，分析了边坡失稳的演化过程，并揭示了荷载由基桩向边坡传递的机理，进而采用强度折减法对边坡稳定性进行评价，给出了局部失稳和整体失稳的判据.随后，谢强课题组［72-75］结合稳定坡角法、有限元法及强度折减法等，分别对宜万线清江大桥［72］和野三河大桥［73-74］岩质边坡的稳定性进行评价；进而结合三维有限元法和模型试验，提出了桥基安全临坡距公式和桥基位置设计方法及其简明计算表格［75］.此外，由于以往研究大多将桥梁桩基边坡简化为平面问题来分析，未能考虑空间效应，冷伍明课题组［76］结合三维数值方法、传统理论和经验公式，提出了一种桥梁桩基边坡稳定性的综合评价方法.张彬等［77］开展离心模型试验，揭示了深度不均匀沉降范围对桩基础变形破坏特性的影响机制及相应的破坏机理.近期，湖南大学课题组［78］采用有限元极限分析法，分析了水平地震系数、土体强度、边坡几何性状、桩顶荷载等对桩-坡系统破坏模式及稳定性的影响，并给出了可评估桥基边坡地震稳定性的详细设计表格.

4.3 加固处治措施

桥梁桩基边坡的稳定性要求、加固措施以及重点加固部位与自然边坡存在显著差异.在桥梁上部结构施工过程中，一方面，须在桥位的滑动带周边布设监测点，以便随时监控滑动带的发展情况；另一方面，应随时关注地质状态的变化，复核勘察设计期间的资料，以便及时调整原设计方案.针对稳定性难以满足要求的工程，可采用抗滑桩、锚杆、帷幕注浆、急流槽、注浆钢花管、仰斜式排水管、预应力锚索、滑动带注浆、喷射混凝土、水平向排水系统及加强钢筋网等单一或综合处治措施进行加固.例如，冯忠居等［79］运用BOZOZUK 分析标准，对桥梁墩台周边堆载导致的桥基偏斜现象进行评价，并采用预应力锚索和预应力抗滑桩的综合处治措施对桥墩进行了纠偏.毕继红和吴丽艳［80］采用ANSYS 软件，分析了列车荷载对桩基边坡的三维动力作用，提出了以预应力锚索加固李子沟特大桥的桩-坡系统.蒋关鲁课题组［81-82］结合模型试验和数值模拟，分析出后排抗滑桩对成兰铁路某桥基边坡的加固效果优于前排抗滑桩，前排抗滑桩仅在靠近桥基时，才能充分发挥加固作用［81］；在此基础上，分析不同频率和加速度峰值条件下桥梁桩基和抗滑桩的受力变形规律，揭示了滑坡破坏发展过程和动力响应特性，并给出了前、后排抗滑桩与桥基的合理距离［82］.

5 展 望

由于陡坡段桥梁桩基承载特性相当复杂，本文通过对近年来陡坡段桥梁桩基设计方法和施工技术的简要回顾，重点介绍其承载机理、试验方法、受力变形分析及其设计计算方法、施工技术和安全评价方法及加固处治措施.在此基础上，相关研究主要可从如下几方面发展：

1）由于陡坡效应的存在，临坡侧一定深度范围内m值和p-y曲线将发生弱化，该观点目前已受到广泛认可.然而，m值和p-y曲线的弱化规律复杂，不仅随深度变化，还与坡度和临坡距密切相关，目前尚未有较为统一的分析方法.显然，m值和p-y曲线的弱化规律、临界深度和临界临坡距等陡坡效应影响范围仍是陡坡段桩基研究的重点之一.

2）陡坡地段的边坡自重、邻近堆载等将对桩基础产生侧向土压力.在滑裂面尚未形成时，可将其视为附加土压力；而在滑裂面已形成时，侧向土压力将发展成滑坡推力，此时桥梁桩基起到了阻挡支护作用，桩-坡相互作用机理相当复杂.换言之，侧向土压力的性质和大小将随桩-坡体系的稳定性发生变化，但现行规范及相关研究尚未给出较为明确的计算方法.

3）陡坡段桥梁桩基承受竖向及水平荷载，且其自由段往往较长，P-Δ效应显著，在设计计算时不容忽视.此外，受陡坡效应的影响，桩基屈曲稳定性及桩基陡坡稳定性分析方法、有效桩长及嵌岩深度计算方法均不同于平地桩基和抗滑桩.

4）群桩承载特性相当复杂，与基桩数量、排列方式以及承台刚度等因素有关.但目前的陡坡段桥梁桩基研究大多针对单桩或双桩，对群桩受力变形特性及桩-土共同作用机理、荷载传递规律等的研究甚少，尚无公认的设计计算方法，有待进一步探讨.

5）陡坡段桥梁桩基的试验研究多局限于室内模型试验，现场试验寥寥可数，有待进一步开展现场试验探究桩-坡系统的荷载传递机制及桩-土相互作用机理.

6）软弱土、填土、黄土、单溶洞或串珠状溶洞及膨胀土地层等特殊环境具有不同于一般砂土或黏性土地层的工程性质，如软弱土的高压缩性和触变性、填土的不均匀性、黄土的湿陷性等.即使桩基处于一般软土或黏土地层中，也可能出现砂黏土互层等复杂工况，而目前的模型试验大多在均质砂土或黏性土中开展.

7）在动力荷载作用下，陡坡段桥梁桩基的桩-坡体系破坏模式可能发生改变，引起陡坡效应影响深度与桩前地基抗力及桩后附加土压力分布产生明显变化，故动力荷载下陡坡段桩基的桩周土体弱化机制研究已成为中西部山区桥梁桩基设计中亟待解决的问题.