基于并行SPH 方法的地震滑坡对桥桩的冲击作用
2022-08-19王占彬张卫杰张健代登辉高玉峰
王占彬,张卫杰,张健,代登辉,高玉峰†
(1.岩土力学与堤坝工程教育部重点实验室(河海大学),江苏南京 210098;2.南京交通职业技术学院建筑工程学院,江苏南京 211188)
伴随着我国经济的高速发展,公路和铁路等基础设施的建设和运营需要更安全的自然环境.据交通运输部统计,截至2019 年,我国公路桥梁总里程达60 634.6 km,铁路桥梁总里程数超过1 100 km.为振兴和发展西部地区经济,我国积极推进西部大开发和丝绸之路经济带战略,两大战略分别涉及山地面积455 万km2和429 万km2(按各省份山地面积比例计算得出).桥梁是沟通山区城市的最主要方式之一.桥梁建设和正常运营对边坡稳定环境的要求不断提高.
我国处于环太平洋地震带和欧亚地震带之间,地震频发.截至2019年,我国发生有5人以上死亡或因灾损失达到当地GDP 0.1%以上的地震灾害近30年平均每年4 次,累计影响人次达0.75 亿,直接经济损失达1 060 亿美元.地震导致了大量滑坡事件,桥桩结构因滑坡冲击发生破坏的现象屡屡出现,如1976 年唐山7.8 级地震中横跨蓟运河的汉沽铁路桥因河岸滑移严重导致桥墩倾斜;2008 年汶川地震滑坡导致10 座桥梁破坏严重或损毁,如都汶公路新房子大桥、一碗水中桥、顺河大桥等受滑坡冲击出现倾斜、剪断、倒塌等不同程度损坏[1],213 国道百花大桥软弱场地土层向河心滑移导致桥桩基础变位、倾斜[2].桥桩结构对滑坡体冲击荷载的承受力大小决定着它能否安全运行,因此研究地震荷载下边坡滑坡冲击桥桩结构过程具有重要意义.
目前,学者们对地震等诱发滑坡对桥桩等结构形成的冲击主要以模型试验、理论解析、数值分析为手段进行研究.在模型试验方面,王友彪等[3]通过调整滑动体中黏土、砂土、砾土和水的质量分数研究土水混合体密度、滑动形态对桥墩承受冲击荷载的影响.在理论解析方面,有学者假设冲击荷载与作用在结构物上静压力成正比[4],但因在理论上冲击荷载是动力问题而非静力问题,该假设未能得到后续较深入的研究.同时也有学者[5]认为该冲击荷载在数值大小上与结构物承受的静压力和滑坡体滑动速度的平方成正比.在数值分析方面,基于网格离散的数值方法如有限单元法、有限差分法等在处理流滑大变形问题时将遭遇困难,故越来越多的学者开始采用无网格分析方法对土体的大变形动力学特性进行研究,其中一些研究(如Huang 等[6]、Dai 等[7]、Hu等[8]、王斌等[9])利用具有无网格近似、追踪粒子信息和能够较好模拟不同材料相互作用性质的光滑粒子流体动力学(Smoothed Particle Hydrodynamics,简写为SPH)方法与流变模型结合,对地震诱发滑坡的大变形流滑过程进行了数值模拟.Bui等[10]在对岩土体材料滑坡大变形、Chen 等[11]在对岩土颗粒材料滑坡大变形的SPH 研究过程中,岩土体材料的应力应变关系采用非关联流动法则Drucker-Prager 模型进行描述.Huang 等[12]在对滑坡中液化土体的大变形土体流滑数值模拟研究中采用土-水耦合SPH 方法,土和水分别在不同的计算层,土体采用弹性模型,水体被视为近似不可压缩流体.唐宇峰等[13]采用SPH 方法对土体滑动大变形规律进行研究,土体应力应变关系采用Drucker-Prager 模型进行描述.Dai 等[14]引入流体-结构相互作用SPH 模型计算研究了文家沟和洪春沟滑坡对节制坝的冲击影响,滑动土体采用Bingham 流体模型.综合分析,学者们基于SPH 方法对流态性滑坡的大变形运动特性研究在一定程度上揭示了滑坡的大变形成灾机制,但是这些研究缺少地震滑坡冲击桥桩结构全过程的演化机理分析.
对此,本文基于SPH 基本原理提出用于模拟分析地震滑坡冲击桥桩结构灾变过程的并行SPH 计算方法,形成自编程序,采用Arias 烈度增加值方法截取地震波以减少计算空间的浪费,基于该方法研究不同地震加速度幅值、频谱和持时条件下滑坡对桥桩结构的冲击规律,并研究不同线程数对并行计算效率的影响.
1 并行SPH地震滑坡冲击模型的建立
1.1 SPH滑坡冲击的基本原理
SPH 方法是一种拉格朗日无网格近似方法,将计算区域划分为一定数目的粒子,每个粒子都包含着自有的场变量,如速度、应力、压力、质量、密度等.实体运动、变形等所有信息由这些粒子承载,同时追踪每个粒子的运动,无网格及粒子间相互作用的特点使其更易处理大变形问题.SPH 无网格近似过程(如图1 所示)包括核近似和粒子近似,假设场函数为f(x),则它的核近似和粒子近似表达式分别如式(1)(2)所示:

图1 SPH无网格近似示意图(目标粒子影响域为半径为κh的圆形区域)Fig.1 SPH approximate schematic diagram(the influence domain of target particle is a circular area with radius κh)
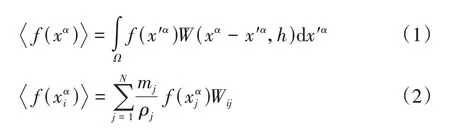
式中:上标α表示坐标方向;特征宽度参数h是定义光滑核函数影响区域的光滑长度;W是光滑核函数;N是粒子i影响域内的粒子数量;mj、ρj分别是粒子j的质量、密度;Wij是粒子i在粒子j位置的值.
SPH 方法的基本控制方程包括连续方程、动量方程和能量方程[15].本研究中将地震滑坡冲击桥桩结构的过程假设为等温过程,因此不考虑能量方程,得到无网格近似后的连续方程、动量方程表达式如式(3)(4)所示:

式中:表示α方向上的体力(如重力)、面力(如外荷载)在i粒子处引起的加速度;分别为速度、应力.
为了提高SPH 计算方法在边界上的精度,将控制方程表达式用影响域内粒子核函数和的形式进行归一化[16-18],得到:
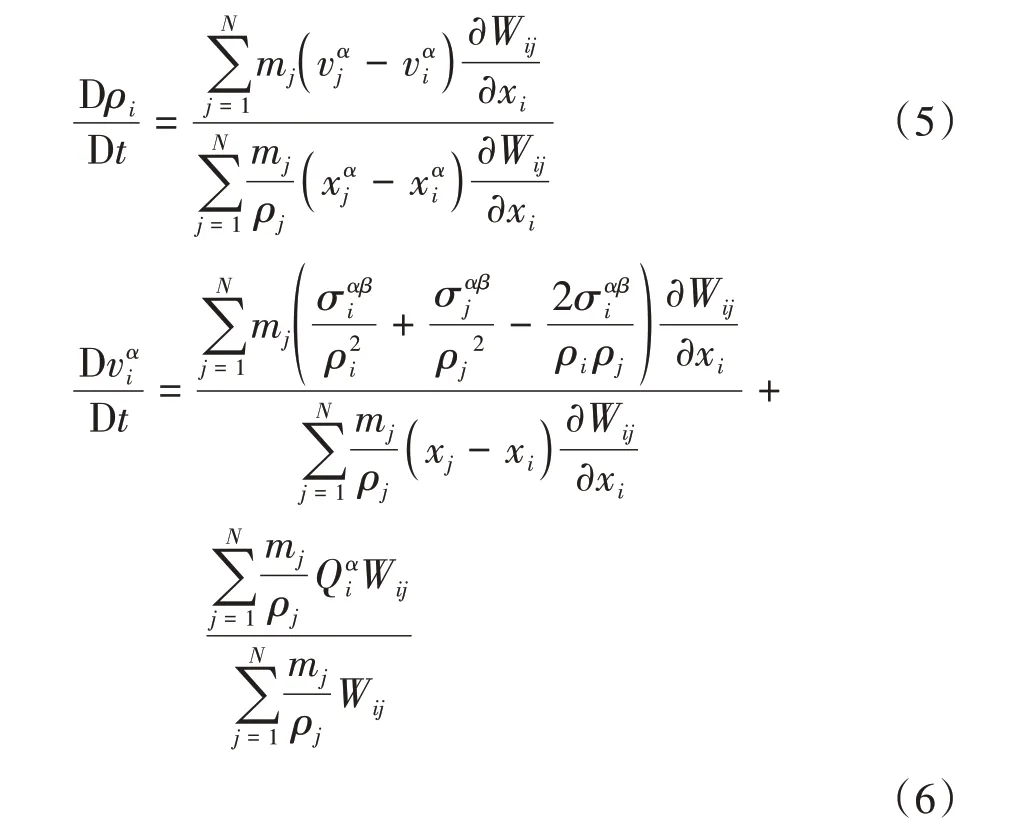
1.2 SPH滑坡冲击的土-结构模型
研究中结构粒子的控制方程采用的应力形式为Piola-Kirchhoff 第一应力张量,质量守恒和动量守恒以完全Lagrange 方法表示,采用的归一化表达式如式(7)(8)所示:


式中:含下标“0”的变量表示初始构形的状态变量;为Piola-Kirchhoff 第一应力张量;Ji为变形梯度的行列式.
由滑动土体对结构体的冲击动量方程得到:

通过影响域内为土体粒子的无网格粒子近似得到如下形式表达式:


式中:等号右侧分子上第一项是土体压力;第二项是土体粒子与结构粒子相对速度产生的压力为结构粒子的加速度.
1.3 SPH滑坡冲击的并行优化
Amdahl 定律给出了算法在运用并行计算之后,运行加速的估算[20].假设算法按串行计算消耗的时间为t1,按并行计算消耗的时间为tp,tp分为并行计算部分和非并行计算部分,其中非并行计算部分的时间为ts,则可得到

式中:N是并行处理器的数量.得到加速比sp:

式中:假设并行处理器数N趋近无穷大时,加速比为sp=t1/ts.这反映了并行程序的加速比主要受限于非并行计算部分的时间ts,也显示出了算法的运行中并行计算的部分占比越多,所消耗的时间越少.本研究采用张卫杰等[21]提出的并行计算方法.
1.4 SPH滑坡冲击的地震加速度施加和验证
本研究中土体采用的Drucker-Prager 模型是Bui等[10]改进的弹性-完全塑性土体本构模型.地震边坡滑坡研究中土体阻尼系数和弱化指数借鉴Chen[22]对地震边坡滑坡的研究.验证模型中采用下负荷屈服面剑桥模型[23],参数如表1 所示.计算模型两侧边界设置为吸能边界,以此防止地震波传播到边界时,边界再反射回来对试验模型或计算模型造成影响(如图2 所示,左侧为刚体边界,右侧为吸能边界),以模拟实际场地的半无限区域特性,地震波由底部输入,振动方向为水平.
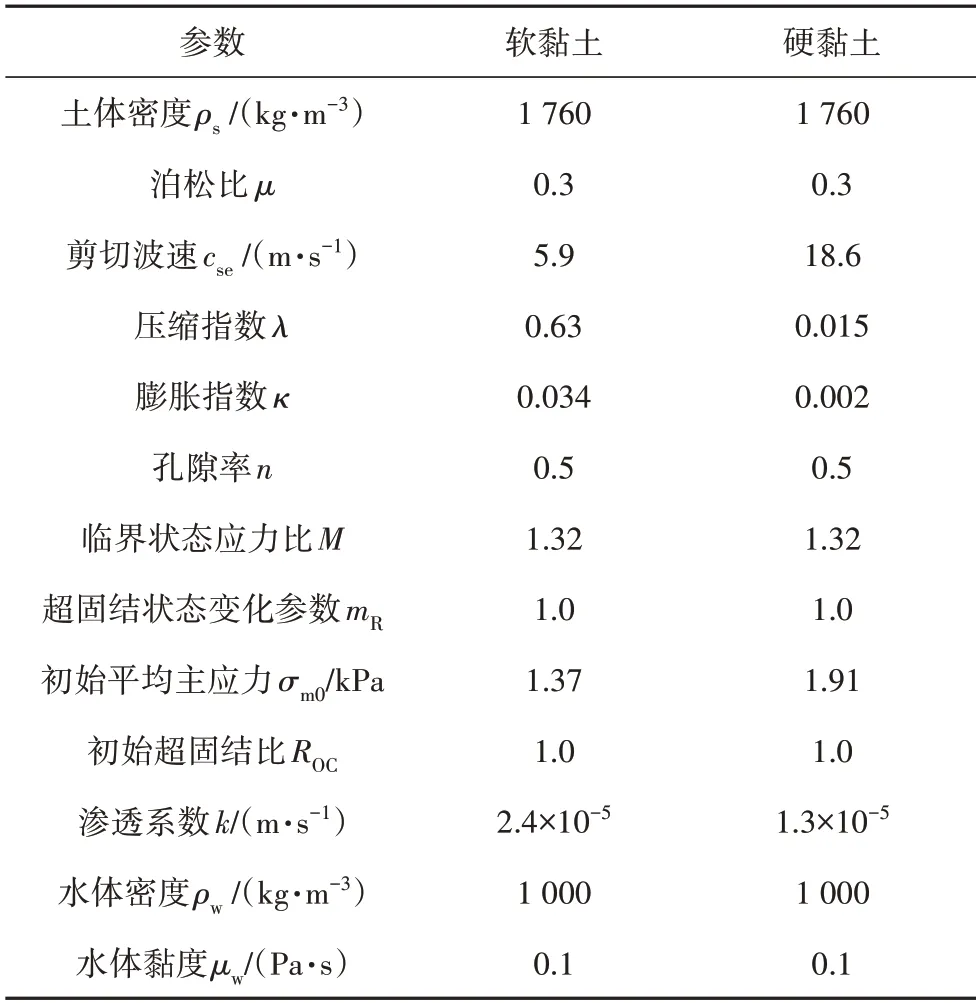
表1 边坡振动SPH模型参数Tab.1 Parameters of SPH model slope vibration
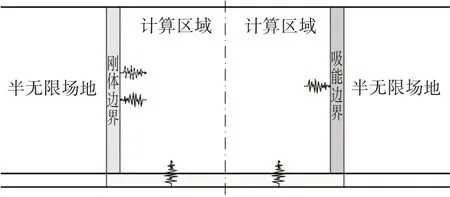
图2 吸能边界与刚体边界模型示意图Fig.2 Schematic diagram of energy absorption boundary and rigid body boundary
为验证所提出方法在地震作用下土体大变形滑坡方面的应用,建立边坡振动SPH 模型如图3 所示.输入的地震波采用修正Kobe 波,地震加速度为水平向.计算模型滑动土体部分由砂土粒子和软黏土粒子间隔等间距分布、硬土层由砂土粒子和硬黏土粒子间隔等间距分布,软黏土和砂土混合而成的边坡土体厚度为20.1 cm,坡度为27.9°,硬黏土和砂土混合而成的边坡土体左侧厚4.8 cm、右侧厚28 cm.模型箱宽1.6 m,高0.384 m.初始粒子间距0.8 cm,软黏土粒子数为1 267,硬黏土粒子数为1 211,砂土粒子数为2 479,水体粒子数为4 957,地震边界粒子数为897.左右两侧各设置3 层吸能边界粒子,其数值为270.砂土密度为2 130 kg/m3,采用Drucker-Prager 模型,剪切波速79.5 m/s,泊松比0.3,内摩擦角30°,渗透系数1×10-4m/s,软黏土和硬黏土采用能够描述软化和硬化行为的下负荷面剑桥模型,材料参数如表1所示,混合土体密度均为1 760 kg/m3,混合土体为饱和状态,计算结果与振动台试验数据(Wartman等[24])进行对比.
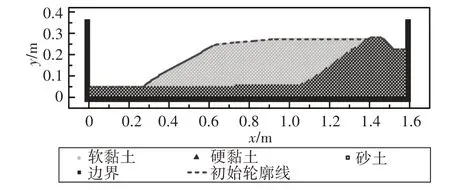
图3 边坡振动SPH模型Fig.3 SPH model for slope vibration
图4 和图5 分别给出了振动后土体粒子分布图和振动后土体粒子最大剪应变云图.从图4 中可以看出,计算结果振后软黏土粒子外轮廓线与物理模型试验振后土体轮廓线较接近,表明计算模型的振后土体滑动位移与物理模型的土体滑动位移大致相近.试验土体变形较计算值大,原因是试验中软化土层的下部和硬化土层的上部分别被嵌附一层0.5 mm厚光滑的高密度聚乙烯土工膜作为预设滑动面,从云图中可以看出,土体最大剪应变位置沿软化土层和硬化土层接触面出现,由此可得出结论:计算值和试验值的土坡滑动规律大致相同.
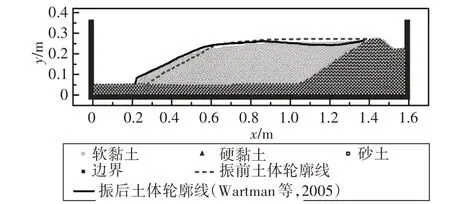
图4 振动后土体粒子分布图Fig.4 Soil particles distribution after vibration
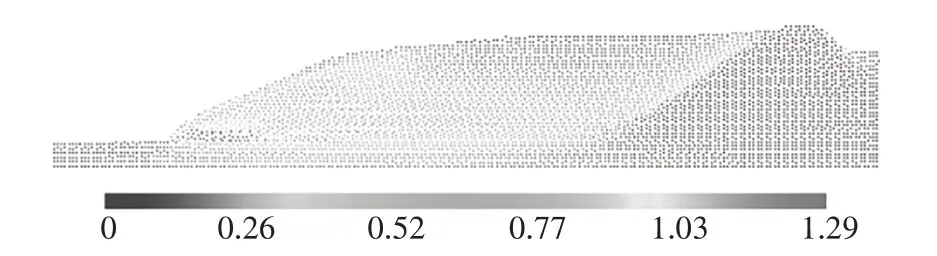
图5 振动后土体粒子最大剪应变云图Fig.5 Maximum shear strain cloud figure of soil particles after vibration
1.5 SPH滑坡冲击桥桩结构的数值模拟工况
Arias 烈度(Ia)[25]是反映观测点地震加速度产生能量大小的重要指标,Ia综合考虑了地震动幅值、地震动频率和地震动持续时间的影响,已被很多学者[26-28]用于地震边坡滑坡潜在危险分析.0.8g峰值加速度的Kobe 地震波加速度持续时间为42 s,时程曲线如图6 所示,其Arias 烈度达0.583 m/s,在5.29~20.29 s 时段内Arias 烈度增长幅度为0.575 m/s,占总增长的99.02%,说明该地震在此测点15 s 时间段内能够释放大部分的能量.选取5.98~20.98 s时段Kobe地震波和全时程地震波作为计算模型的地震动输入.后文将42 s Kobe 地 震波和5.29~20.29 s 时段Kobe地震波分别简称为Kobe波和Kobe截取波.

图6 0.8g峰值Kobe地震波加速度时程及Arias烈度曲线Fig.6 Acceleration time history and Arias intensity curves of 0.8g Kobe seismic wave
本研究计算采用的地震峰值加速度为0.2g、0.4g、0.6g、0.8g;地震反应谱以时间变化系数的形式进行改变:0.5、1.0、2.0;地震持续时间选取1 次和叠加2次相同的典型时段截取波.
2 地震滑坡对桥桩结构的冲击规律
2.1 原波与截取波荷载下滑坡结果对比
为比较Kobe 截取波和Kobe 波在本研究算例的差别,选取5.98~20.98 s时段Kobe地震波和全时程地震波作为计算模型的地震动输入,建立模型如图7所示.布置4 个边坡测点和1 个边界测点,编号分别为S1、S2、S3、S4、B1,其中S1、S2 分别是42 s Kobe 地震波和15 s Kobe截取地震波计算模型总位移最大值点,S3、S4 分别是边坡坡脚和坡顶的测点,B1 用于测量边界在施加42 s Kobe 地震波和15 s Kobe 截取地震波加速度之后得到该点的位移,验证地震加速度施加情况.

图7 Kobe截取波SPH地震计算模型Fig.7 SPH seismic calculation model with Kobe intercepted wave
如图7 所示,所建模型采用的粒子间距为0.25 m,粒子总数为13 623,其中滑动土体粒子数为8 592,桥桩结构粒子数为1 350,边界粒子数为3 681.土体采用DP 模型,参数见表2.边界测点B1 施加两种地震波后的计算结果如图8、图9 所示,从图中可看出SPH 测得位移时程与实际加速度积分后得到的理论值基本一致,随着时间的推移,理论位移偏移终值分别为0.05 mm、-20.56 mm,SPH 计算值分别为1.23 mm、-41.15 mm,位移累积偏移差值分别为1.18 mm、-20.59 mm.

图8 42 s Kobe波边界测点B1输出位移时程Fig.8 Displacement time history of boundary point B1 under 42 s Kobe wave

表2 边坡振动SPH模型参数Tab.2 Parameters of SPH model slope vibration
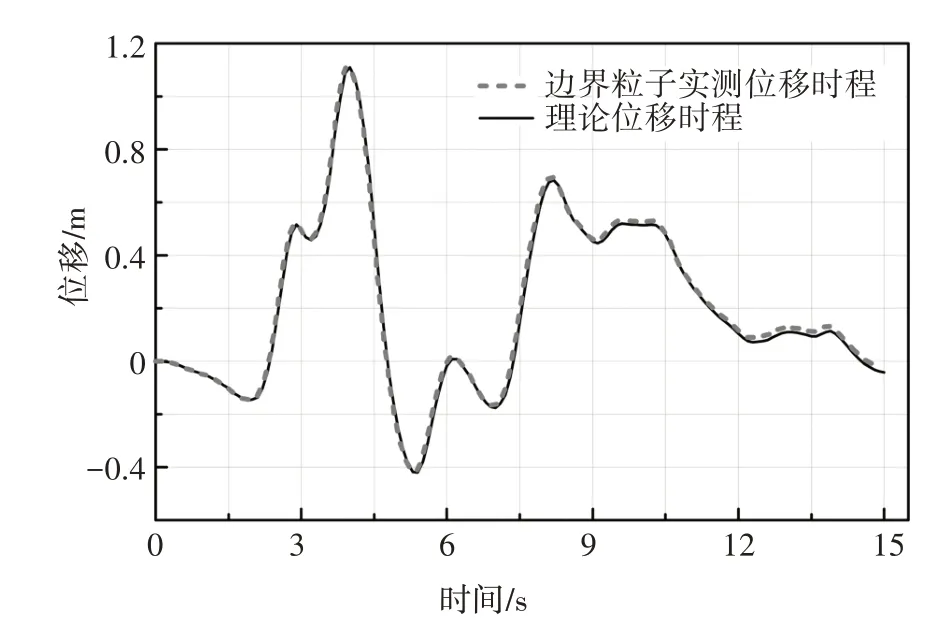
图9 15 s Kobe截取波边界测点B1输出位移时程Fig.9 Displacement time history of boundary point B1 under 15 s Kobe intercepted wave
图10~图13 分别给出了4 个测点S1、S2、S3、S4在42 s Kobe 波和15 s Kobe 截取波作用下的水平向和竖向位移对比.从图中可以看出S1 测点15 s 地震波输入工况相较于42 s 地震波输入工况在水平向和竖向存在最大3.4 s 的延迟位移,42 s 地震波输入工况最大水平位移为40.60 m、竖向位移为-15.29 m,15 s 地震波输入工况最大水平位移为40.42 m、竖向位移为-14.58 m,水平向和竖向最大位移差分别为0.18 m、0.71 m,差值占比分别为0.44%、4.65%;S2 测点15 s 地震波输入工况相较于42 s 地震波输入工况在水平向和竖向存在最大3.4 s 的延迟位移,42 s 地震波输入工况最大水平位移为40.54 m、竖向位移为-15.36 m,15s 地震波输入工况最大水平位移为40.53 m、竖向位移为-14.72 m,水平向和竖向最大位移差分别为0.01 m、0.64 m,差值占比分别为0.02%、4.14%;S3 测点15 s 地震波输入工况相较于42 s 地震波输入工况在水平向和竖向存在最大3.3 s的延迟位移,42 s地震波输入工况最大水平位移为34.30 m、竖向位移为-13.76 m,15 s地震波输入工况最大水平位移为34.10 m、竖向位移为-13.97 m,水平向和竖向最大位移差分别为0.20 m、0.21 m,差值占比分别为0.58%、1.53%;S4 测点15 s 地震波输入工况相较于42 s 地震波输入工况在水平向和竖向存在最大3.5 s的延迟位移,42 s 地震波输入工况最大水平位移为24.84 m、竖向位移为-19.81 m,15 s 地震波输入工况最大水平位移为23.57 m、竖向位移为-19.73 m,水平向和竖向最大位移差分别为1.27 m、0.08 m,差值占比分别为5.12%、0.40%.
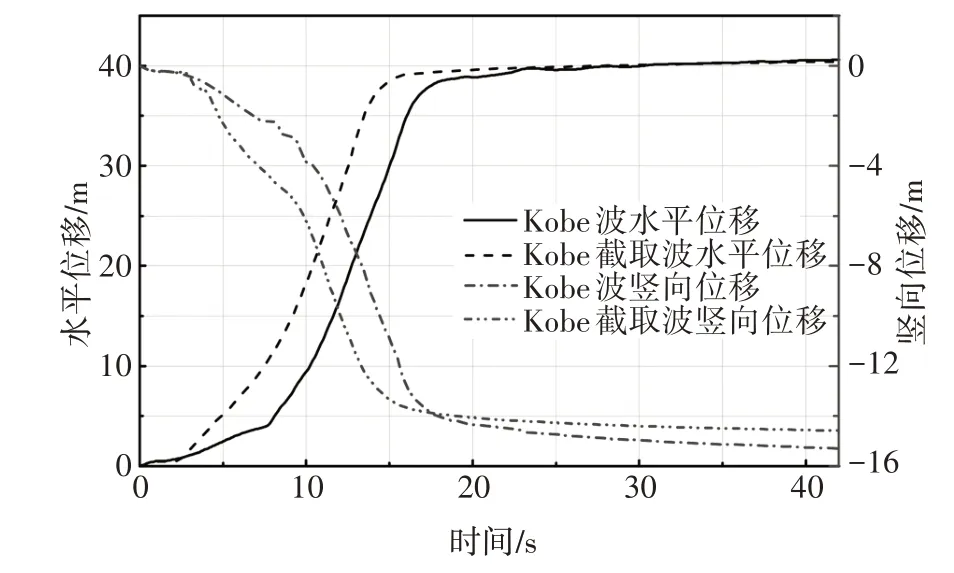
图10 42 s Kobe波和15 s Kobe截取波边坡测点S1位移对比Fig.10 Displacement comparison at S1 in slope under 42 s Kobe wave and 15 s Kobe intercepted wave

图11 42 s Kobe波和15 s Kobe截取波边坡测点S2位移对比Fig.11 Displacement comparison at S2 in slope under 42 s Kobe wave and 15 s Kobe intercepted wave
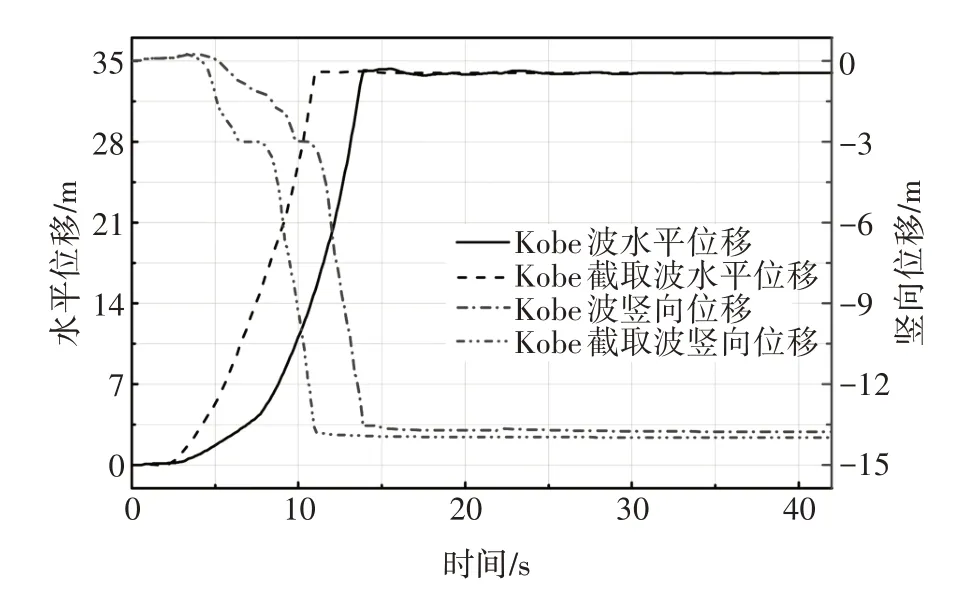
图12 42 s Kobe波和15 s Kobe截取波边坡测点S3位移对比Fig.12 Displacement comparison at S3 in slope under 42 s Kobe wave and 15 s Kobe intercepted wave
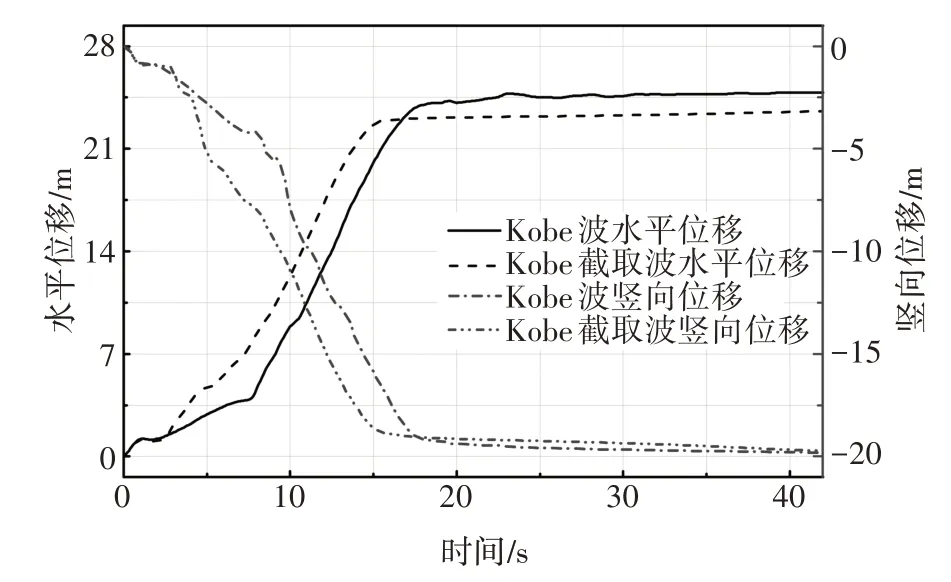
图13 42 s Kobe波和15 s Kobe截取波边坡测点S4位移对比Fig.13 Displacement comparison at S4 in slope under 42 s Kobe wave and 15 s Kobe intercepted wave
图14、图15 分别给出了两种地震波作用下的总位移云图.从图中可以看出滑动土体粒子的位移规律是相似的,即滑动机理没有因为截取地震波输入而出现与原波差距较大的变化.由两者的计算结果比较可知桥桩结构所受荷载、滑动土体位移在两种地震动输入情况下相差很小,为提高研究效率,选取此15 s 时段地震加速度作为本小节数值模型计算研究的地震输入.

图14 42 s Kobe波地震荷载下计算模型总位移云图(单位:m)Fig.14 Total displacement cloud figure of calculation model under 42 s Kobe wave(unit:m)
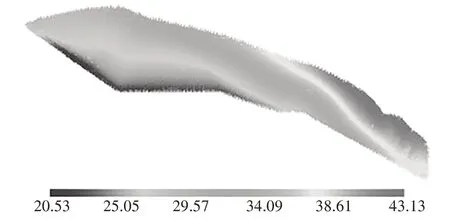
图15 15 s Kobe截取波地震荷载下计算模型总位移云图(单位:m)Fig.15 Total displacement cloud figure of calculation model under 15 s Kobe intercepted wave(unit:m)
2.2 地震加速度幅值的影响
建立计算模型如图16 所示.布置测点S1,坐标(52.75,16.25),用于监测位移变化;布置A-A断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.所研究地震加速度幅值分别为0.2g、0.4g、0.6g、0.8g.土体参数如表2所示.
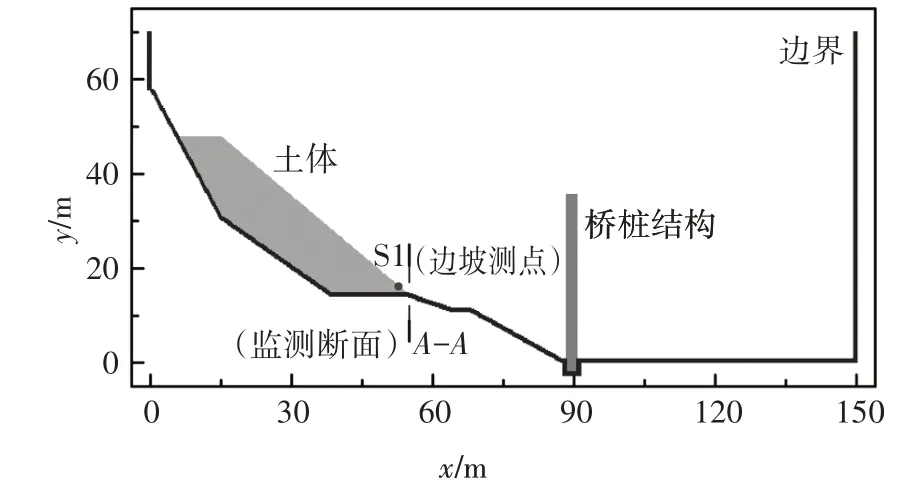
图16 地震加速度幅值影响计算模型及测点布置Fig.16 Model of seismic acceleration amplitude influence and layout of measuring point
图17~图20 分别给出了0.2g、0.4g、0.6g、0.8g峰值加速度作用下的位移云图.从图17、图18 中可以看出,0.2g峰值加速度和0.4g峰值加速度作用下土体最终位移和滑动的土体体积量很接近(0.2g工况S1 测点最大水平向位移为34.71 m,最大竖向位移为-13.89 m;0.4g工况S1 测点最大水平向位移为34.76 m,最大竖向位移为-13.83 m),4种峰值加速度作用下的S1 测点最终位移均很接近的原因是该测点与桥桩结构的水平距离为35.28 m,0.6g工况S1测点最大水平向位移为34.71 m,0.8g工况S1 测点最大水平向位移为35.46 m,与该测点和桥桩结构水平距离相差很小,该测点经过地震荷载作用已滑动到接近桥桩结构的位置.
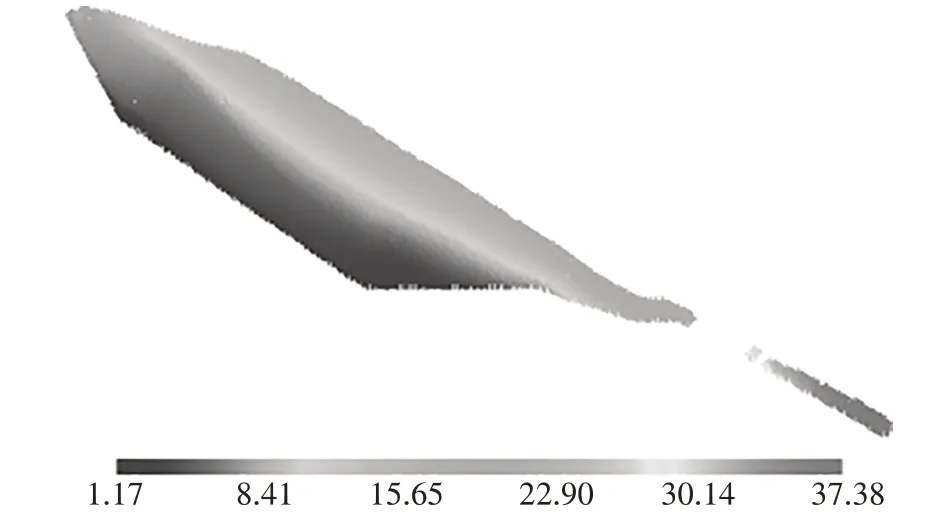
图17 0.2g峰值加速度下计算模型总位移云图(单位:m)Fig.17 Total displacement cloud figure(PGA=0.2g)(unit:m)
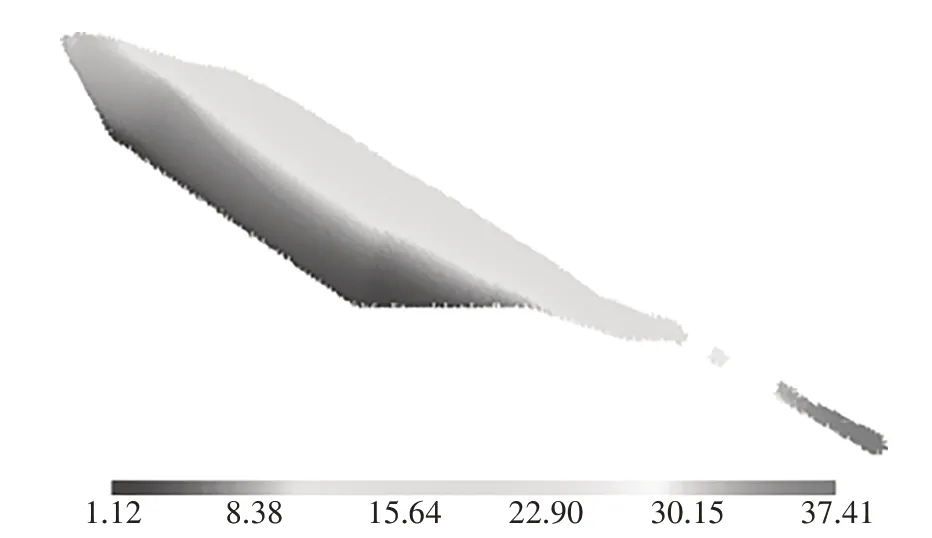
图18 0.4g峰值加速度下计算模型总位移云图(单位:m)Fig.18 Total displacement cloud figure(PGA=0.4g)(unit:m)

图19 0.6g峰值加速度下计算模型总位移云图(单位:m)Fig.19 Total displacement cloud figure(PGA=0.6g)(unit:m)
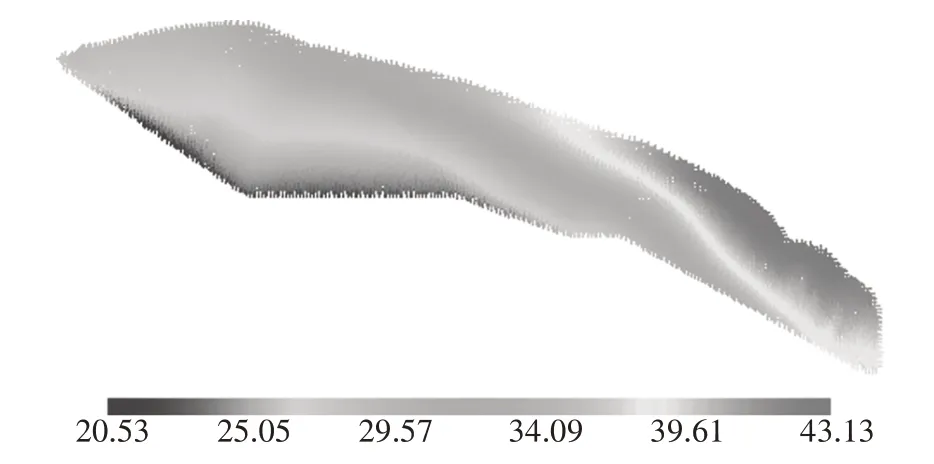
图20 0.8g峰值加速度下计算模型总位移云图(单位:m)Fig.20 Total displacement cloud figure(PGA=0.8g)(unit:m)
图21 给出了4 种峰值加速度作用下S1 测点水平向和竖向位移-时间关系对比曲线,从图中可以看出,0.4g峰值加速度作用下土体位移快速增大的时间要早于0.2g峰值加速度作用下的土体位移快速增大的时间4.2 s.0.6g峰值加速度作用下土体位移快速增大的时间要早于0.2g峰值加速度作用下的土体位移快速增大的时间7.6 s.0.8g峰值加速度作用下土体位移快速增大的时间要早于0.2g峰值加速度作用下的土体位移快速增大的时间9.5 s.这说明峰值加速度的提高加速了边坡的破坏和加大了边坡的滑坡体积量.监测断面A-A,0.2g通过此断面体积量为51.81 m3,占比9.65%;0.4g为54.94 m3,占比10.23%;0.6g为90.19 m3,占比16.79%;0.8g为266.125 m3,占比49.56%.监测断面数据也说明0.2g峰值加速度工况和0.4g峰值加速度工况滑坡体积量很相近,0.6g峰值加速度工况滑坡体积量稍大于0.2g和0.4g工况滑坡体积量,0.8g峰值加速度工况滑坡体积量最大,且超过0.2g工况滑坡5 倍之多.地震加速度幅值的提高在增加土体边坡滑坡体积量的同时,也加快了边坡土体的滑动破坏.
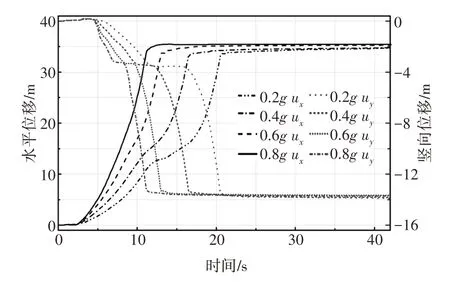
图21 不同峰值加速度下S1测点位移-时间对比曲线Fig.21 Displacement-time comparison curves at S1 under different PGAs
2.3 地震加速度频谱的影响
为研究不同地震加速度频谱对边坡滑坡冲击桥桩荷载的影响,将15 s Kobe 截取地震波压缩至7.5 s和延长至30 s,定义时间变化系数为现研究地震波时长与原时长的比值.本节所选取的时间变化系数tvc为0.5、1.0、2.0.3种时间变化系数的地震加速度时程如图22 所示.它们经过傅里叶变换以频域的形式展示如图23 所示,它们的波峰频率分别为0.27、0.54、1.08,随着时间变化系数的提高,波峰频率增大.计算模型如图16 所示,布置测点S1,坐标(52.75,16.25),用于监测位移变化;布置A-A断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.土体参数如表2所示.
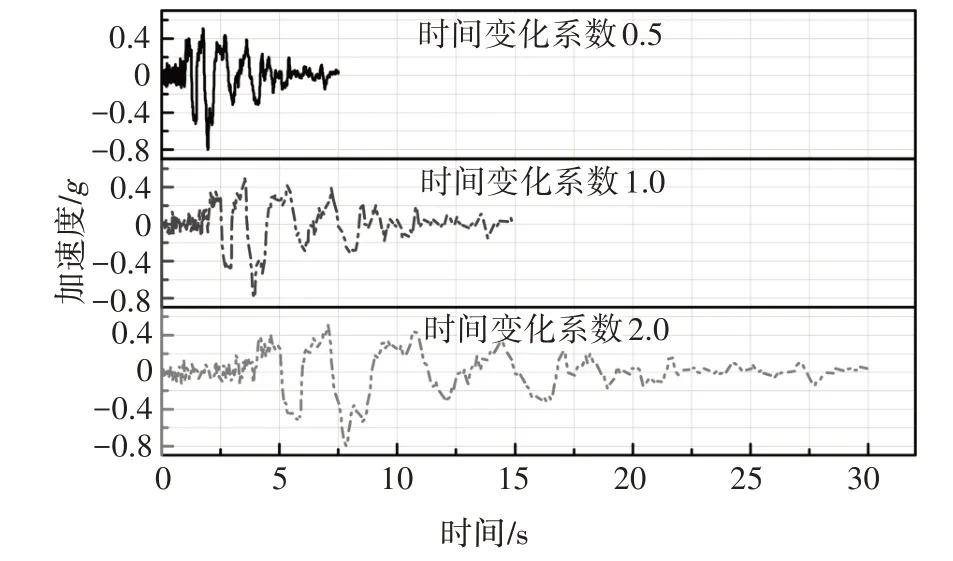
图22 不同时间变化系数下地震加速度时程Fig.22 Seismic acceleration time history under different tvc
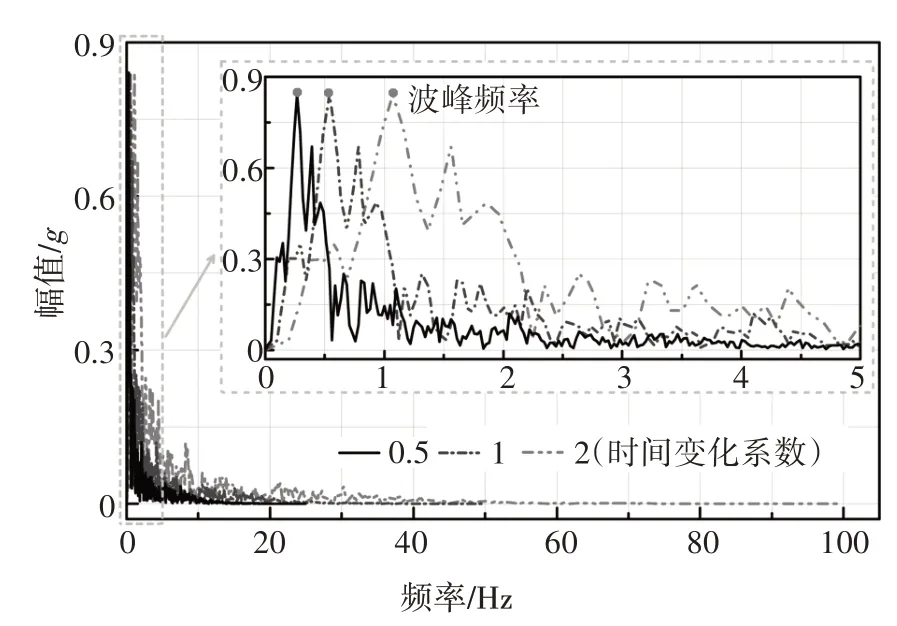
图23 不同时间变化系数下地震反应谱频域分布Fig.23 Frequency domain distribution of seismic response spectrum under different tvc
图24、图25 分别给出了时间变化系数为0.5 和2.0 的边坡地震位移云图,图26 给出了3 种时间变化系数下地震边坡模型S1 测点水平向位移、竖向位移与时间的对比关系曲线.从位移云图中可以看出,时间变化系数为0.5 时最大位移和最小位移分别为37.4 6m、2.05 m,通过断面A-A的体积量为59.31 m3,占滑坡体总体积量的11.05%;时间变化系数为1.0时最大位移和最小位移分别为43.13 m、20.53 m,通过断面A-A的体积量为266.13 m3,占滑坡体总体积量的49.56%;时间变化系数为2.0时最大位移和最小位移分别为43.65 m、17.71 m,通过断面A-A的体积量为273.44 m3,占滑坡体总体积量的46.08%.时间变化系数由0.5 增大至1.0,土体滑坡位移和体积量会明显增多,时间变化系数由1.0 增大到2.0,土体滑坡最终位移和滑动体积量无明显变化.图26 中时间变化系数2.0 相较于1.0 时在15~30 s 出现的水平位移波动由边界位移波动引起,边界位移波动如图9 所示.从中也可以看出,时间变化系数由1.0 减小至0.5,延缓了滑坡体的位移变化(延缓约2.6 s),也减小了滑坡体的滑动速度,时间变化系数由1.0增大至2.0,滑坡位移未出现较大变化,提前约0.9 s,较小程度地提高滑坡体的滑动速度,原因可能是边坡土体在时间变化系数为1.0 的情况下已经达到足够大的滑坡位移.

图24 时间变化系数为0.5计算模型总位移云图(单位:m)Fig.24 Total displacement cloud figure(tvc=0.5)(unit:m)
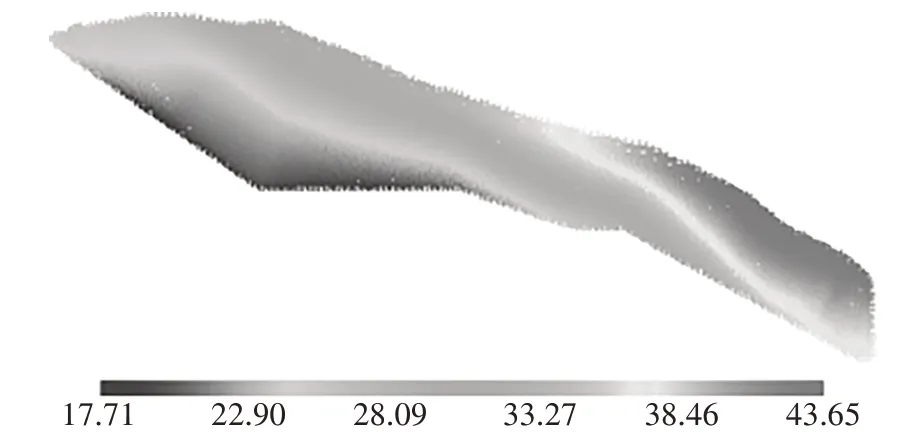
图25 时间变化系数为2.0计算模型总位移云图(单位:m)Fig.25 Total displacement cloud figure(tvc=2.0)(unit:m)

图26 不同时间变化系数下S1测点位移-时间对比曲线Fig.26 Displacement-time comparison curves of measuring point S1 under different tvc
2.4 地震加速度持时的影响
建立计算模型如图27 所示,布置测点S1、S2,坐标分别为(52.75,16.25)和(38.75,28),用于监测位移变化;布置A-A断面,横坐标为54.25,用于监测滑坡土体通过此断面的体积量.所考虑的地震加速度持时影响是选取1 次的15 s Kobe 截取波和2 次截取波时间上的叠加,持续时间分别为15 s、30 s.土体参数如表2所示.
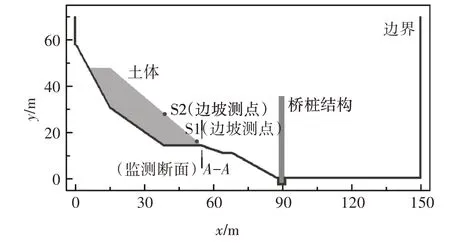
图27 地震加速度持时影响计算模型及测点布置Fig.27 Calculation model of seismic acceleration duration influence and layout of measuring points
图20、图28 分别给出了1 次15 s Kobe 截取地震波和2次叠加截取地震波的位移云图,图29、图30给出了两种持续时间下地震边坡模型S1、S2 测点水平向位移、竖向位移与时间的关系对比曲线.从云图中可以看出,2次叠加截取地震波最终最大和最小位移分别为45.59 m、21.26 m,高于1次截取地震波边坡最大位移和最小位移2.46 m、0.73 m,1 次截取地震波边坡最大和最小位移分别为43.13 m、20.53 m.1次截取地震波和2 次叠加截取地震波滑坡土体通过断面A-A的体积量相同,均为266.125 m3,占滑坡体总体积量的49.56%,滑坡体积量均很大.从位移-时间关系曲线中可以看出,2 次叠加截取地震波与1 次截取地震波作用的边坡,对S1 测点位移的影响差别很小,但对S2 测点在15 s(即第1 次截取地震波作用结束后)出现增大,S2 测点最终水平位移、竖向位移在1次和2次叠加截取地震波作用下分别为40.53 m、14.72 m 和43.03 m、15.06 m,2 次多于1 次2.5 m、0.34 m.这说明2 次叠加截取地震波对滑坡体的中部和后缘部分位移影响较大,对前缘部分无较大影响.
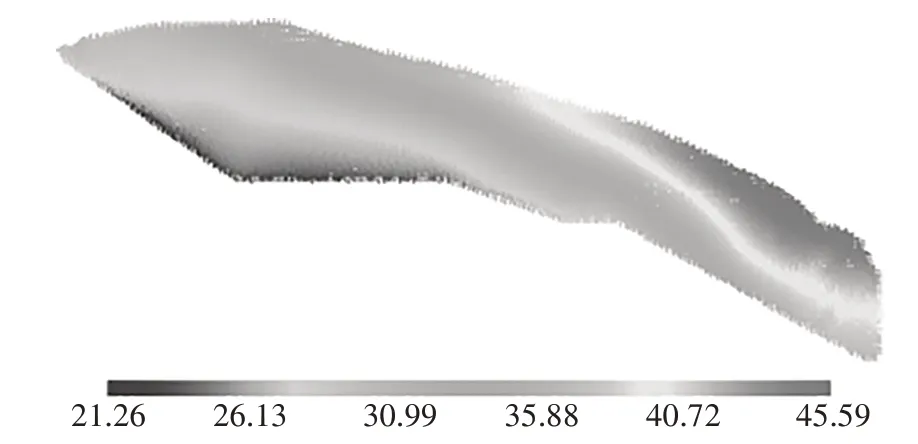
图28 2次截取地震波持时叠加计算模型总位移云图(单位:m)Fig.28 Total displacement cloud figure under wave superposition(unit:m)
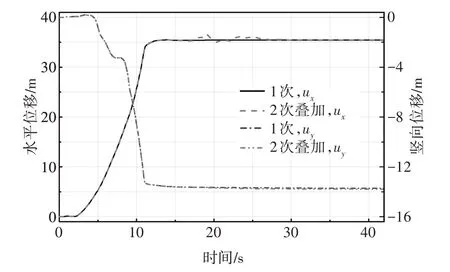
图29 1次和2次截取地震波持时叠加测点S1位移-时间对比曲线Fig.29 Displacement-time comparison curve of S1 under single and superpositioned wave
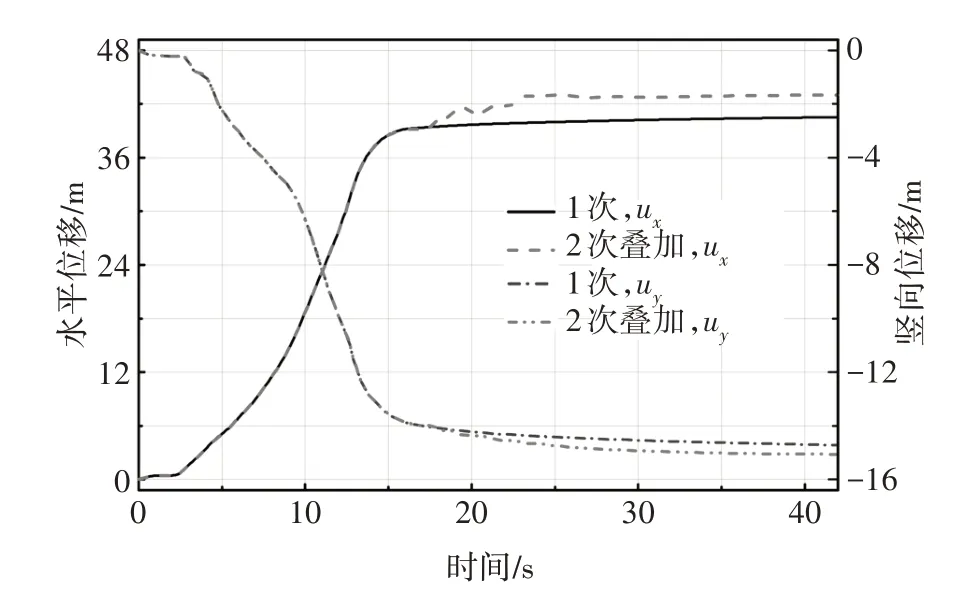
图30 1次和2次截取地震波持时叠加测点S2位移-时间对比曲线Fig.30 Displacement-time comparison curve of S2 under single and superpositioned wave
2.5 SPH滑坡冲击模型的并行优化效率
为验证并行优化的效率,计算研究了线程数分别为1、2、4、6、8、10、12、16、20、24、28,峰值加速度分别为0.2g、0.4g、0.6g、0.8g,时间变化系数Rt分别为0.5、1.0、2.0,施加1 次截取波、循环施加2 次截取波地震作用下边坡土体滑动冲击桥桩结构工况(其中峰值加速度为0.8g,时间变化系数Rt为1.0,1 次15 s截取Kobe 波为同一工况,在图中简写为0.8g),按式(13)得到各线程数下的加速比sp(多线程和单线程计算消耗时间的比值),如图31 所示.图中虚线为加速比随线程数增加的均值趋势线,从图31 中可以看出,在该计算平台下,线程数从1 增加到8,加速比呈快速增长趋势;线程数从8 增加到20,加速比增长速度稍缓;线程数从20 增加到28,加速度增长很缓慢,表明计算中线程数为20~28 时,计算机处理效能的利用已接近或达到最大状态.线程数为28 时最大达6.1,平均5.7,其计算时间近似是单线程计算时间的1/6.该结果说明本研究土-结构耦合SPH 并行方法极大地提高了地震作用下边坡土体滑移计算效率,减少了计算时间.

图31 地震滑坡冲击桥桩结构分析的加速比随线程数的变化曲线Fig.31 Acceleration ratio curve with the number of threads in landslide impact analysis of bridge pile under earthquake
3 结论
1)基于SPH 方法的基本原理,建立了考虑静压力和相对速度产生的压力的土-结构粒子相互作用模型,通过地震滑坡模型验证了SPH 方法模拟振动台试验的准确性.
2)根据Arias 烈度增长值确定15 s 截取Kobe 地震波代替42 s 原Kobe 地震波,减小了对计算空间的浪费.
3)高地震加速度幅值会大幅增加可滑动土体的体积量,0.4g相对于0.2g滑坡体积量增加不明显,0.8g滑坡体积量超过0.2g滑坡5倍之多,低地震加速度幅值会大幅加快滑动速度,0.4g下土体位移快速增大的时间要早于0.2g下的时间4.2 s,0.8g下土体位移快速增大的时间要早于0.6g下的时间1.9 s.
4)地震加速度频率由0.27 增大至0.54,土体滑坡体积量增大近4 倍,滑动位移加快2.6 s,由0.54 增大到1.08,土体滑坡体积量无明显变化,滑动位移加快0.9 s.
5)地震加速度持时对滑坡体后缘部分影响较大,对后缘测点的位移增加明显高于前缘测点,滑动到桥墩结构的累积土体体积量随持时的增加而增加.
6)对多种工况的SPH 程序进行不同线程数的并行优化,总结得出线程数从1 增加到8,加速比呈快速增长趋势;线程数从8 增加到20,加速比增长速度稍缓;线程数从20 增加到28,加速度增长很缓慢,表明计算中线程数为20~28 时,计算机处理效能的利用已接近或达到最大状态.
