基于改进遗传算法的BP神经网络的水体叶绿素a含量预测
2022-08-19周游陆安江刘璇
周游,陆安江,刘璇
(贵州大学明德学院,贵州贵阳,550025)
0 引言
水体富营养化现在越来越严重,表征水体富营养化的指标有很多,其中水体叶绿素a含量是重要指标之一,且水体中叶绿素a含量变化机理是非常的复杂,能够用于判断水体水华的发生情况[1]。我们可以通过对水体中叶绿素a含量影响因子的研究,从而为水污染防治提供关键性依据[2]。目前国内外对水体叶绿素a预测的智能算法发展迅猛,其中,为构建叶绿素a含量的预测模型,我们常常利用神经网络的非线性逼近特征,因此神经网络已经成为叶绿素a含量预测的重要手段之一[3]。例如文献[4]张成成等基于太湖梅梁湾2010年4月至2011年12月的监测数据,提出基于支持向量机的叶绿素a浓度预测模型,并进行了输入变量的敏感性分析,并通过模拟值和实测值的对比分析可得该模型可以较好地预测7天后的叶绿素a浓度的变化情况;文献[5]裴洪平等通过对西湖湖心采样的数据进行处理分析,最终成功构建了叶绿素a的BP神经网络预测模型;文献[6]罗华军等提出利用遗传算法的特性来优化支持向量机的模型参数,同时利用空间重构方法计算出时间序列的时间延迟和嵌入维数,确定支持向量机输入向量的水库叶绿素a浓度短期预测模型;文献[7]李峰等对三峡水库支流神龙溪2013年5月至12月水环境进行检测,并对检测数据进行处理分析,利用Matlab R2010a软件建立了基于BP神经网络的叶绿素a预测模型。本文通过改进遗传算法的选择、交叉以及变异算子,从而优化BP神经网络权值和阈值,最后建立叶绿素a含量预测模型。
1 BP神经网络
BP神经网络是由Rumelhart和McClelland为首的科学家在1986年提出的一种按照误差逆向传播算法训练的多层前馈式网络,是目前被使用最为广泛的神经网络[8],同时被广泛应用于藻华预测领域。本文采用三层前馈神经网络来构建叶绿素 a 含量预测模型[9]。基本结构如图1所示。图1 中输入变量与隐含层之间的权值为Wik,Vk表示隐含层与输出层之间的权值;B1表示隐含层阈值矩阵,B2表示输出层阈值矩阵,φ ( x )表示隐含层,∅ ( x )表示输出层节点传递函数。

图1 BP神经网络的结构
通过文献[10-12]可知,BP 神经网络是一种迭代算法,它的传播由两个过程组成,第一个是正向传播,即输入信息在传播过程中通过相应的权值、阈值和激活函数的处理,最后传输到输出层;第二个过程是逆向传播过程,当输出误差大于给定的精度时则转入误差反向传播,在误差返回传输过程中,网络将会对各层的权值和阈值进行修正,经过反复上述操作直到满足给定精度。其中,x1, x2,… ,xn作为初始信号,对于在本文中的输入变量,我们使用与叶绿素a含量相关的因子监测值,将叶绿素a含量作为输出变量;对于网络中的激活函数,其中隐含层采用tansig函数作为激活函数,输出层采用线性函数purelin作为激活函数,权值和阈值学习函数在本文中采用learngdm函数。
则在单组样本中,隐含层神经元k的输入值为输入变量与隐含层权值乘积之和,如式(1)所示:

经激活函数激活映射后,节点k的输出值为:
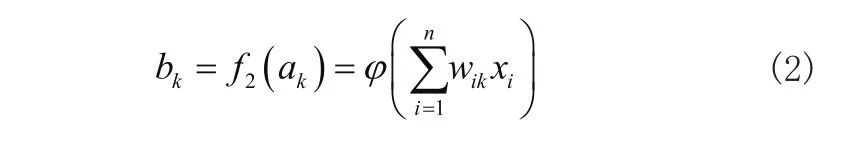
输出层的输入值为隐含层输出值与输出层权重Vk乘积之和,如式(3)所示:

输出层叶绿素预测输出值为:

对于叶绿素a预测模型的准确性,本文采用Pearson相关系数来对其进行评估,具体关系如式(5)所示:

通过文献[13-14]可知,对于处理数据BP神经网络虽具有较强的自适应、泛化以及非线性映射能力,但其自身具有以下缺点:网络训练工程中及其容易陷入局部极小值、误差梯度变化非常小以及收敛速度特别慢。而遗传算法具有较强的全局搜索最优值特性[15],因此考虑利用遗传算法来优化BP 神经网络。
利用遗传算法全局优化能力,对于BP神经网络的初始权值和阈值我们可以通过遗传算法的选择、交叉和变异操作来进行优化,从而得到BP神经网络的最优权值和阈值。BP神经网络的权值和阈值由遗传算法获得的最优个体进行赋值,局部优化由BP神经网络预测模型进行,通过遗传算法和BP神经网络的结合最终得到BP神经网络的全局最优预测值。
2 改进的遗传算法优化BP神经网络
遗传算法是一种效仿自然界遗传与选择机制的随机优化算法,它结合了自然遗传学的适应性或器官进化过程与功能优化。通过仿照达尔文进化过程中染色体结构的“适者生存”,通过随机信息交换寻找最优染色体(解)。在每一代人中,都有一套新的人工染色体是用最合适的旧染色体碎片创造出来的。它能有效地利用历史信息推测新的搜索点,预期性能会得到改善。
在使用遗传算法时,种群规模是有限的,通过选择、交叉以及变异后,往往会使适应度值较高的个体在下一代中得到更多的复制,这样反复的进行,会造成某些个体在种群中占有绝对的优势,遗传算法就会不断强化这种优势,从而造成群体开始收敛,造成种群多样性不断降低,使个体变得越来越相似,最终导致好的个体得不到更多繁殖的机会,使得遗传算法出现局部最优,这就是所谓的遗传算法早熟现象。
遗传算法基本上是从一个最普通的群体遗传学模型中衍生出来的。完成遗传算法主要依靠三个相关算子:选择、交叉和变异。因此针对遗传算法的缺点,本文将对遗传算法的选择、交叉以及变异算子进行改进。遗传算法主要步骤及改进措施如下所示。
(1)编码
确定编码方式是遗传算法进化设计的首要步骤,经分析研究我们决定在实数编码和二进制编码中选择一种编码方式,考虑到二进制编码的复杂性及计算量大的缺点,本文最终决定采用实数编码。
(2)适应度函数的设计
确定适应度函数,适应度函数在遗传算法中的作用就好比眼睛对于人的作用,对适应度函数改进所产生的的效果可以很好的反应在算法中。适应度函数选取的好坏直接影响到问题解决的完美与否,因为遗传算法的进化仅仅取决于适应度函数,个体能否进入候选群完全由适应度决定,适应度与个体的优劣程度成正比,适应度越高,个体越优秀,进入下一代的概率越高,越有利于种群的繁衍。通常来说,不同的适应度函数对同一问题的效果是不同的,我们往往根据我们要实现的目的来选择相应的适应度函数。对于本文我们采用期望输出值与网络输出值的误差Eg作为评价标准[16]:

(3)免疫机制选择算子
算法早熟会导致无法得到全局的最优解,为了得到最优解,克服算法早熟,本文对选择概率进行了轻微的变动,利用的是一种免疫原理。免疫优化算法结合了生物免疫系统的进化机制和传统的遗传算法,在一定水准上精确地提升了算法的性能。利用免疫机制进行选择时,目标函数和约束条件就相当于免疫系统中的抗原,在抗原的刺激下可产生抗体群,之后根据遗传操作和抗体亲和度找出针对该抗原的抗体。
首先定义个体浓度d:


设某一个个体的适应度为 fi,该个体被选中的概率为pfi,则:
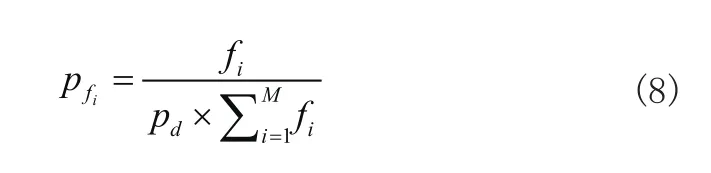
其中,i=1 ,2,3,…,M
通过对个体浓度进行定义,选出最优个体会变得相对方便,同时也提高了选择的效率和精确率。由上述可知,适应度与被选中的概率成正比;个体浓度与被选中的概率成反比,它们分别可以实现加快收敛速度和防止过早收敛的目的。
(4)自适应交叉、变异算子
在种群寻找最优解的过程中,会产生大量具有相同的适应度值染色体,也就意味着会找到很多相似的个体,相似个体越多,种群的多样性就会越低,针对这一现象设计出了自适应交叉、变异算子:

Pc1、Pm1初始设置的交叉概率、变异概率,C1和C2是非零的正常书。这里C1=0.1,C2= 0 .01,NCSF表示当前种群具有最多相同适应度值的染色体数目,fCSF表示当前种群中最多的适应度值,favg表示当前种群的平均适应度值。
可以看出如果种群中产生了数量多且适应度值大于种群平均适应度值,则证明种群中存在很多优秀的个体,这时适当减少交叉变异概率,以保持种群的优势;如果种群中产生了大量低适应度的个体,则使之保持较大的交叉变异概率,一方面提高种群多样性,另一方面可以创造更大产生优质个体的概率。
叶绿素a预测模型中,改进的遗传算法优化BP神经网络步骤如下:
Step1:确定BP神经网络结构参数。
Step2:初始化种群。设定种群规模,编码BP神经网络的权值和阈值,产生初始种群。
Step3:确定适应度函数。适应度函数作为评价个体好坏的标准利用适应度值判断每条染色体适不适合在现在的环境中生存。本文采用式(1)作为适应度函数。
Step4:选择过程。选择操作是以每条染色体的适应度值作为参考,其中适应度较高的个体“脱颖而出”的机会就越大,然后“升级”为父代参与到下一代群体。对于选择过程中的概率,本文采用式(3)作为个体被选择的概率。
Step5:交叉过程。交叉就是在一定交叉概率上,锁定两条父代染色体,并将其部分基因互相移植,从而得到新生个体的过程。通过交叉操作,可以较大程度上提高遗传算法获取最优解的可能,本采用式(4)作为交叉算子产生新个体。
Step6:变异过程。变异是交叉操作的拓展延伸步骤,其目的都是为了保证种群多样性。变异也是在一定的变异概率上,瞄准某条染色体,使它的某个基因发生骤变的过程。与交叉有所不同的是,变异只针对单个个体,交叉针对的是两个个体;且交叉是大概率创造新个体,变异是小概率创造新个体。在变异操作时如果变异概率设置过大,遗传算法就可能简化为随机搜索算法,遗传算法的特性与搜索能力将不复存在。本文采用式(5)作为变异算子产生新个体。
Step7:判断是否满足终止条件,如满足则输出最有值;如不满足则重复Step2~ Step6过程。
基于改进的GA-BP神经网络的预测模型结构如图2所示。

图2 基于改进的GA-BP神经网络的预测流程
3 模型的训练与应用
3.1 数据预处理
本文采用数据来源于贵州省西部威宁县县县城西南面的草海,采集对象为该水域2018年7月1日到8约时间10日的时段水质因子叶绿素a(Chl-a)、水温(Tw)、pH值、溶解氧(Do)、总氮(TN)、透明度(SD)、总磷(TP) 以及降雨量(RF)等8项现场监测数据,数据采集频次为每小时一次。
在使用BP神经网络进行网络训练之前,我们必须对原始数据进行归一化处理,因为原始数据各因子存在着量纲及数量级不同的缺点。处理数据归一化的方法有很多,本文采用极差归一化处理,归一化公式如下[17]:

试中:x′表示为监测数据归一化后[0,1]空间映射值;x为监测数据原始值;xmin,xmax分别为最大、最小监测值。
3.2 网络变量选择
3.2.1 因子敏感性分析
为了使网络变量尽可能的少,接下来将对影响叶绿素a含量变化的主要敏感因子进行探讨。对于叶绿素a含量变化主敏感因子探讨依据,由于Dimopoulos因子敏感性秩序具有合理性,因此本文采用基于偏导的Dimppoulos敏感性分析方法进行模型敏感度分析[18]。
通过Dimppoulos敏感性分析方法分析,训练结束的神经网络为系数明确的函数表达式,因此在单样本中,叶绿素a含量各相关因子敏感值可通过以下表达式求出[19]:

式中:Si为神经网络第i个输入变量的敏感值;(x1,x2,…,xn)为叶绿素a含量预测值,x1,x2,…,xn为叶绿素a含量变化相关因子监测值;ak分别为神经网络隐层,c输出层输入值矩阵。
则对于在总样本中,叶绿素a相对于对该变量的敏感度可用以下式子进行表示:
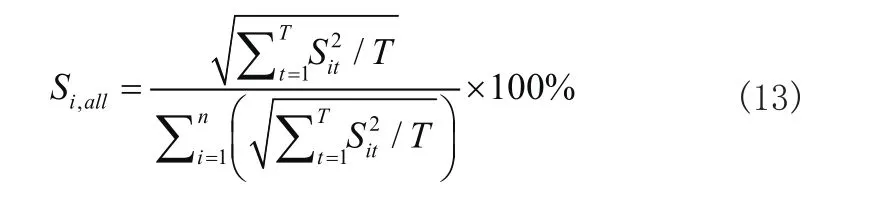
式中:Si,all为总样本中第i个因子相对敏感度,值越接近1对叶绿素a含量变化影响越大;Sit为样本t第i个输入变量的敏感值,n为叶绿素a含量相关因子数,T为样本总数。
基于 Dimopoulos 因子敏感性分析结果如图3所示,叶绿素a含量对pH值最为敏感,TN次之,Tw、Do再次之,而对SD、TP及RF三项指标敏感性最弱。

图3 叶绿素a相关因子敏感性分析分布
3.2.2 输入因子方案选择
根据dimopoulos因子的灵敏度顺序,将输入变量由小到大,调整输入参数的个数,设置不同因子的输入精简方案。对于叶绿素a预测模型中的其他设置固定不变,进行基于神经网络的1000次循环训练。如表1输入因子调整方案。

表1 输入因子调整方案

3 pH、TN、Tw、Do、SD 5 0.973 4 pH、TN、Tw、Do 4 0.985 5 pH、TN、Tw 3 0.965
从表1可以看出,剔除SD、TP和RF三项指标,预测精度基本保持不变,表明SD、TP和RF不是叶绿素a含量变化的主敏感因子。
结合图3和表1的分析,本文采用方案4作为网络输入因子来对叶绿素a含量进行预测。
3.3 改进GA-BP神经网络性能训练
在700余组有效数据种选取500组为训练数据,200组作为验证数据;本文采用方案4,以叶绿素a含量为输出变量,以pH、TN、Tw和Do,4项因子作为输入变量训练神经网络。其中,神经网络隐含层神经元数K=4,最大迭代次数设置为1000,学习率设置为0.1,训练目标最小误差设置为0.0001;GA种群规模设置为100,进化次数为100,初始交叉概率Pc1= 0 .8,初始变异概率Pm1= 0 .1。具体的测试结果见下图。
通过图4~图7可以看出,改进后的GA-BP神经网络具有较好的预测效果,其中改进GA-BP神经网络的训练精度为0.985,仿真精度为0.981,GA-BP神经网络的训练精度为0.973,仿真精度为0.965;对比基础BP神将网络,BP神经网络的训练精度为0.959,仿真精度为0.934。改进GA-BP神经网络相对于GA-BP神经网络预测精度提升1.23%,仿真精度提升1.66%;GA-BP神经网络相对于BP神经网络预测精度提升1.46%,仿真精度提升3.32%;改进GA-BP神经网络预测精度相对于BP神经网络预测精度提升2.71%,仿真精度提升5.03%;从结果可得改进GA-BP神经网络预测模型优于GA-BP神经网络预测模型,GA-BP神经网络预测模型优于BP神经网络预测模型。
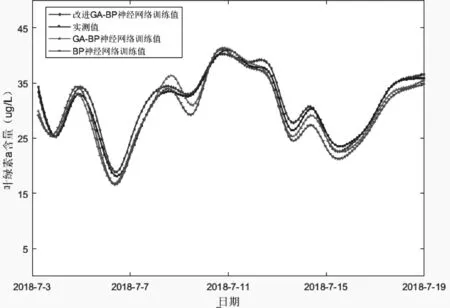
图4 训练效果

图5 训练值与监测值相关性

图6 仿真效果
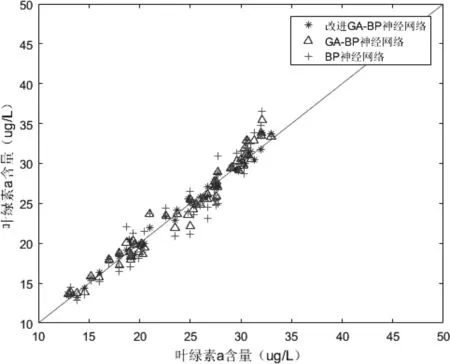
图7 仿真值与监测值相关性
4 结论
本文通过对遗传算法选择、交叉及变异算子的改进,并将改进的遗传算法与BP神经网络结合构建了叶绿素a预测模型。从BP神经网络、GA-BP神经网络及改进GA-BP神经网络的仿真与训练结果对比可得,通过对遗传算法算子的改进可以有效避免遗传算法陷入局部最优及早熟现象,同时对BP神经网络的权值和阈值进行了有效的优化,避免网络训练陷入局部最优并提高了模型预测精度,从而提高了叶绿素a预测精度;本文通过Dimopoulos偏导敏感性分析,对叶绿素a预测模型中的输入因子进行敏感性分析,根据灵敏值大小调整输入因子个数,最终确定输入因子个数及因子组合。
