基于“材料力学”课程教学的高阶思维训练案例设计——以“预应力圆环热驱自持续翻滚”为例

李 凯，杜长慎，柳军修，余 勇，葛大丽

(安徽建筑大学土木工程学院,安徽合肥 230601)

0 引言

教育部自2019年起开始全面实施一流本科课程建设，一流课程(金课)建设引领着全国高校教育教学改革的发展方向.一流课程的主要特征概括为“两性一度”，即高阶性、创新性和挑战度，其核心在于以“创新性”为方法，通过具有“挑战度”的训练，达到培养“高阶性”思维的目的[1].培养高阶性思维作为一流课程建设的首要目标，其不同于传统的知识识记、理解和应用的培养目标.高阶性思维培养目标要求学生通过对挑战性问题进行独立思考和深入探究，提出独立个性化的见解和认识，以训练形成创新性和批判性思维模式.高阶性思维训练案例是实现一流课程建设目标的重要途径和关键环节.案例设计时，内容上应反映学科前沿性和时代性，难度上应具有一定挑战度，形式上应能有效引导和激发学生思考、讨论和探究，最终培养学生解决复杂问题的创新能力和高阶性思维[2].

“材料力学”是土木、机电、材化和航空等多个工科专业的一门专业基础课，对后续专业课的学习至关重要.材料力学作为独立学科是以意大利科学家伽利略在1638年发表《关于力学和局部运动的两门新科学的对话和数学证明》一书为标志，现已发展成为一门古老、经典且理论框架成熟的学科[3].传统材料力学课程注重基本概念和公式推导，难以调动学生学习兴趣并且容易束缚学生思维.近年在“材料力学”课程的讲授内容、教学方法和考查手段等方面已有不少改革和创新，如实物演示[4]以及引入力学史[5]等.目前这些尝试也已取得不少效果，但还需不断探索以达到一流课程建设要求.

“材料力学”一流课程打造的关键在于围绕“两性一度”特征做好高阶思维训练的案例设计.力学及相关学科在近几十年不断涌现各种新成果，为培养学生创新意识与批判精神提供丰富优秀素材，可用于激发学生的学习兴趣和探究热情.为此本文选择趣味性强、课程内容相关度高和具有一定挑战度的“热响应性预应力圆环自持续翻滚”问题[6]作为案例进行重构整合，从材料力学基本问题出发逐步推进到科学前沿问题，展示问题升阶和启发思考的高阶思维训练案例设计过程.

1 基本问题

本案例从材料力学中梁的弯曲基本问题出发进行设计[7].如图1(a)所示，一根初始长度为L、横截面半径为R的圆柱细杆首先被纯弯曲成圆环状，接着细杆两端面被相互粘结在一起，并形成一封闭圆环.此时，封闭圆环处于纯弯曲状态且其内部存在预应力.假设L>>R，细杆弯曲成圆环过程中材料变形较小，仍属于弹性变形阶段，不考虑屈服后塑性变形阶段，圆环的拉压弹性模量为E.细杆弯曲成圆环后，圆环横截面上的环向应力和环向应变属于拉压应力和拉压应变，不属于切应变.求此预应力圆环横截面上的环向拉压应变及拉压应力.

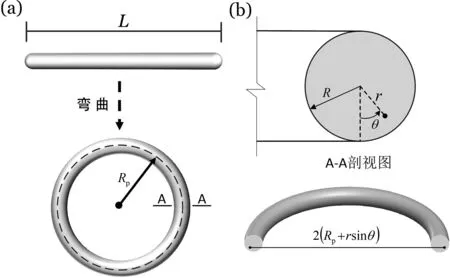
图1 圆柱细杆被纯弯曲为预应力圆环Fig.1 A thin cylindrical rod is purely bent into a prestressed torus

该基本问题涉及梁理论中的横截面正应力计算.首先，截取半圆环进行受力分析，根据对称性和平衡条件易得预应力圆环横截面上的轴力为零.因此，预应力圆环轴线的周长等于细杆的初始长度L.设弯曲后圆环曲率半径为Rp，则L=2πRp.在圆环横截面内建立如图1(b)所示的极坐标系，并进一步求解圆环横截面任意位置(r,θ)处的环向拉压应变.

把此预应力圆环分割成无数根环向纤维，环向纤维弯曲前的长度为细杆的长度L.细杆弯曲成圆环后，圆环横截面(r,θ)处的环向纤维周长变为2π(Rp+rsinθ)，如图1(b)所示.根据拉压应变定义，则环向拉压应变可以计算为

(1)

注意到细杆长度与圆环曲率半径之间的关系为L=2πRp，则公式(1)可进一步化简为

(2)

从公式(2)可看出，圆环横截面上环向拉压应变随角度周期性变化，且上下对称.特别地，圆环横截面上环向拉压应变在内侧区域为压缩应变，在外侧区域为拉伸应变.

利用梁理论中的单向受力假设，圆环横截面上任意点处的环向拉压应力与环向拉压应变成正比.因此，环向拉压应力可计算为

(3)

从公式(3)可看出，与环向拉压应变对应，圆环横截面上环向拉压应力在内侧区域为压缩应力，在外侧区域为拉伸应力.

2 进阶问题一

在基本问题的基础上，进一步进阶求解此预应力圆环在给定非均匀温度作用下的环向拉压应力.如图2所示，将上述预应力圆环置于一平面热台上，且圆环以角速度ω稳定翻转.此时，在预应力圆环内会形成一非均匀温度场，此非均匀温度场由文献[8]直接给出.求此时预应力圆环在非均匀温度场下横截面上的弯矩分量Mx.

图2 置于热台上的预应力圆环Fig.2 A prestressed torus placed on a hot surface

此题为热力耦合问题，我们首先根据文献给出的温度场求解得到横截面上的环向拉压应变和拉压应力，然后将环向拉压应力对x轴取矩计算预应力圆环横截面上的弯矩分量Mx.

2.1 预应力圆环横截面的温度场

预应力圆环在平面热台上稳定翻转时，其内部的温度场由文献[8]直接给出，这里不进行详细推导.计算内部温度场时，假设预应力圆环与平面热台间接触传热，且热流量为Q.假设预应力圆环表面其余部分以热对流的形式向空气散热,且不考虑流体力学中气体流动的传热系数.计算温度时，以环境温度为参考温度计算圆环内各点处的相对温度，则圆环横截面上的相对温度分布可写为[8]

(4)

式中的bern、bein分别为开尔文函数的实部和虚部，A0、An、Bn分别表示为

(5)

式中的h为传热系数，k为材料的热传导系数，D的表达式为

(6)

根据公式(4)，图3绘制了不同角速度下预应力圆环横截面上的温度分布.数值计算中，参数根据文献中已有实验选择典型数值，分别为R=5×10-4m，Q=10×103W/m2，h=10 W/m2/oC，c=103J/kg/oC，k=0.1 W/m，ρ=103kg/m3和ω0=0.25/s[6].从图3可见，圆环横截面上的温度场大小和分布受到翻转角速度的明显影响.一般地，翻转角速度越大，圆环横截面上温度场的顶部与底部温度差越小.

图3 不同角速度时圆环横截面上的温度场Fig.3 Temperature fields on the cross section of a torus for different angular velocities

2.2 预应力圆环横截面上的拉压应变和拉压应力

下面计算上述温度场下预应力圆环横截面上的环向拉压应变和环向拉压应力.热应力问题是材料力学中的难点，准确理解总应变、热应变和弹性应变三个重要概念是求解热应力问题的关键.总应变一般由几何条件可以直接确定，而热应变与温度相关.弹性应变为总应变与热应变之差,且与弹性应力成线性关系.

由于预应力圆环横截面上的温度场是非均匀的，因此圆环受热后其曲率半径会发生变化.假设圆环受热后其曲率半径从Rp变为Rc，则环向总拉压应变可类似于公式(2)由几何条件计算为

(7)

从公式(7)可见，预应力圆环横截面上的环向总拉压应变仍随角度周期性变化，且上下对称，在内侧区域为压缩应变，在外侧区域为拉伸应变.

假设预应力圆环受热后，其横截面上的拉压热应变与温度成正比，则圆环横截面内的拉压热应变可计算为

εT(r,θ)=CTT(r,θ)

(8)

其中CT为材料的热膨胀系数.

由总应变等于热应变与弹性应变之和，代入公式(7)和(8)，拉压弹性应变可计算为

(9)

进一步地，利用单向受力假设，预应力圆环受热后其横截面上的环向拉压应力σ(r,θ)可计算为

(10)

从公式(10)可见，环向拉压应力与横截面上的温度相关.

2.3 预应力圆环横截面上的弯矩分量Mx

由公式(10)中已给出的环向拉压应力分布可进一步计算横截面上的弯矩分量Mx.根据材料力学梁弯曲理论，横截面上的环向拉压应力σ(r,θ)对x轴取矩并进行积分即得横截面上的弯矩分量

(11)

联立公式(2)、(4)-(11)可得Mx的解析形式为

(12)

从公式(12)可看出，横截面上的弯矩分量Mx的大小与翻转角速度相关.

3 进阶问题二

下面，进一步进阶求解预应力圆环的热驱自持续翻转问题.如图4所示，将上述预应力圆环置于一平面热台上，圆环内部会形成非均匀温度场，则其横截面上弯曲力偶Mx能驱动预应力圆环发生自持续翻转.假设预应力圆环稳定翻转的角速度为ω，求圆环与热台之间的滑动摩擦系数.

此问题是个动力学平衡问题.首先求解施加在圆环微段两端面上的弯曲力偶的合力偶，其是驱动圆环翻转的驱动力.然后建立圆环稳定翻转时驱动力与摩擦阻力之间的平衡方程，再根据已知的角速度反向推算圆环与热台之间的滑动摩擦系数.

3.1 预应力圆环稳定翻转时的驱动力偶

选取预应力圆环微段dx为研究对象，圆环微段两端横截面上分别受弯曲力偶Mx作用，如图4所示.注意到小曲率假设条件下,sin(α/2)≈α/2=dx/2Rc.则两端面横截面上的弯曲力偶的合力偶为两端面力偶矢量Mx的矢量和，方向沿环向，大小可计算为

(13)

注意到M合作用在圆环微段dx上，则预应力圆环每单位长度上的驱动力偶可计算为

(14)

公式(14)表明，驱动力偶为横截面上弯曲力偶Mx与圆环曲率之积.弯曲力偶Mx越大，驱动力偶越大.驱动力偶也随曲率增加或曲率半径减小而增加.

将公式(12)中的弯曲力偶Mx带入公式(14)，得到驱动力偶的解析形式为

(15)

从公式(15)可见，驱动力偶Md也与圆环的翻转角速度相关.特别地，驱动力偶与膨胀系数和拉压弹性模量成正比.这个结果意味着，提高膨胀系数和拉压弹性模型是提升驱动力偶的重要途径.

3.2 平衡方程及滑动摩擦系数

预应力圆环在稳定翻转过程中，除了受到热致驱动力偶的作用外，其还受到热台表面对其施加的滑动摩擦力.由于圆环处于动力学平衡状态，可建立微段的平衡方程来求得滑动摩擦系数.首先取圆环的任意微段作为研究对象，由圆环微段重力为G=ρgπR2dx，故单位长度的圆环受到的滑动摩擦力大小可计算为[9]

Ff=CfρgπR2

(16)

其中，Cf为预应力圆环与平面热台间的滑动摩擦系数.

当圆环稳定翻转时，圆环处于平衡状态.选取单位长度圆环为研究对象，并对y轴建立力矩平衡方程，可得

Md=FfR

(17)

联立公式(15)-(17)并化简可得预应力圆环与平面热台之间的滑动摩擦系数为

(18)

值得注意的是，公式(18)中圆环曲率半径Rc应受到滑动摩擦力和横截面上非均匀温度场的双重影响，其可由圆环横截面上的轴力条件进行确定.选取半圆环作为研究对象进行受力分析，根据半圆环在轴力与滑动摩擦力的共同作用下的平衡条件，易得轴力为FN=LCfρgπR2/2，则

(19)

将公式(10)中的环向拉压应力代入(19)可得预应力圆环稳定翻转时的曲率半径为

(20)

公式(20)表明，预应力圆环在热驱稳定翻转时，其曲率半径与受热及滑动摩擦都相关.对于热膨胀材料，受热膨胀和滑动摩擦都导致圆环曲率半径增大.

通过公式(18)和(20)进行数值计算，图5绘制了预应力圆环热驱稳定翻转时的角速度与相应滑动摩擦系数间的依赖关系.计算中，参数根据文献中已有实验选取了典型数值，分别为R=5×10-4m，κ=20 m-1，CT=3×10-3/oC，E=10 MPa，ρ=103kg/m3，Q=3×103W/m2，k=0.1 W/m，h=5 W/m2/oC，ρ=103kg/m3和g=10 N/kg[6,10].从图5可见，随着预应力圆环翻转角速度的增加，对应的滑动摩擦系数是单调减小的，此结果符合物理直觉.一般地，滑动摩擦系数减小，圆环稳定翻转所需的驱动力偶也减小.又因驱动力偶随着圆环翻转角速度增大而减小.这样，热流不变的情况下，圆环可以获得更大的翻转角速度.

4 小结

本文以“预应力圆环热驱自持续翻滚”问题为例，将现代力学前沿研究成果巧妙嫁接到“材料力学”课程教学中，通过递进式、创新型和启发性的案例设计方式，展示了高阶思维训练案例设计模式.此教学案例已被应用于“材料力学”示范课项目，初步成果表明可加强学生对书本原有基础知识的理解，开阔学生的学术视野，以及培养他们的创新精神和批判意识.在教育教学改革探索实践中，还可根据各学校及专业特点进行个性化设计，最终达成知识结构与能力两方面的专业培养核心目标.