沉积层结构被动源探测方法及其在典型盆地的应用
2022-08-19张瑞青况春利张笑晗李永华
张瑞青,况春利,张笑晗,李永华
1 中国地震局地球物理研究所,北京 100081
2 中国地震局地震研究所 地震大地测量重点实验室,武汉 430071
3 湖北省地震局,武汉 430071
0 引 言
沉积盆地精细结构探测在油气资源勘探开发、防震减灾、深部结构成像与构造演化研究等方面均具有重要意义. 许多沉积盆地蕴含石油、天然气和矿产资源,是国家能源战略基地. 同时,不少人口和建筑密集的城市也位于沉积盆地地区. 已有研究显示,沉积盆地对“超高、超大、超长”结构的地震动有显著的放大效应. 一旦发生地震,可加剧工程结构的破坏,造成巨大的人员伤亡和经济损失.如1985 年墨西哥海域发生M
8.1 地震,远在400多千米外的位于盆地内的墨西哥城遭受了严重破坏,比震中区的灾害还要重(Flores-Estrella et al.,2007). 一般而言,场地放大作用取决于近地表岩石或土壤的剪切波速度和密度,特别是30~60 m之内的S 波速度对地表地震动的影响极大(王海云等,2008). 因此在抗震设计规范中,用V
(地表以下30 m 的平均土层剪切波速值)参数来指示场地类别. 此外,沉积盆地下方,近地表的低速层会造成远震走时层析成像和接收函数偏移成像的假象. 因此,如何准确获取沉积层结构就显得尤为重要(Chen et al., 1996; Langston, 2003, 2011; Ni et al.,2014; Tao et al., 2014; 滕龙等, 2014).钻探和人工地震勘探(主动源探测)是探测沉积盆地结构的一种经典方法. 前者对沉积层直接进行钻孔测井研究,可以获得浅部地层岩性和速度结构的详细信息. 后者采用人工震源(如炸药、重锤、可控震源和气动震源等)激发地震信号,利用目标层上产生的反射/折射震相,通过动力学射线追踪方法来反演地下结构. 由于S 波震相难以识别,因此人工地震测深通常仅给出P 波速度分层结构信息. 主动源探测成像精度高,但由于成本高、空间覆盖受限、以及炸药震源对环境具有破坏性,因此在城市等人口密集地区实施起来较为困难,同时也难以开展区域尺度结构研究.
近年来,随着密集流动地震台站的观测,基于被动源资料已逐渐成为沉积盆地精细结构探测的一种重要手段. 目前被动源探测的地震学方法主要获得的是地壳浅部的S 波速度结构,对泊松比结构的研究甚少(Wang et al., 2021). 本文通过调研相关文献,对基于被动源资料约束沉积盆地结构的地震学方法进行了一定的归纳总结,并综述了松辽盆地和华北盆地沉积层结构研究的最新进展. 下面将首先对这些方法的基本原理和进展逐一进行阐述.
1 远震体波方法
1.1 接收函数和转换函数
远震接收函数方法是获取台站下方壳幔速度间断面结构的常规手段之一(图1). 它的基本原理是利用间断面上产生的转换波/多次波与直达波之间的到时差来约束间断面结构. 目前P 波接收函数研究中,常采用H
-κ
扫描法求取地壳厚度和平均波速比(Zhu and Kanamori, 2000). 该方法是考虑单层地壳模型情况下,给定地壳P 波平均速度,对一定范围内的地壳厚度(H
)和波速比(V
/V
,也用κ
表示)进行网格搜索,将转换波和多次波振幅进行加权叠加. 构建的叠加函数s
(H
,κ
)如下所示: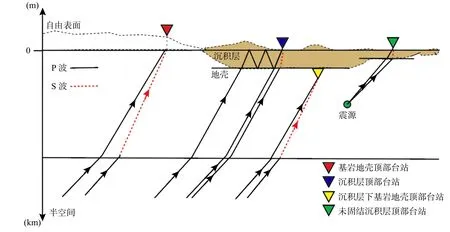
图 1 均匀介质中,不同地震台站(基岩和位于盆地内)下方远震和近震P 波响应的射线路径示意图. 实线表示P 波,虚线表示S 波Fig. 1 Schematic ray paths of the P (black solid lines) and S (red dashed lines) waves beneath stations (located on bedrock and sediment) in response to an incoming P wave both at teleseismic and local distances

ω
(i
=1, 2, 3)是权重因子,且ω
+ω
+ω
=1,RFS(t
)是径向接收函数,t
是Ps、PpPs 和PsPs+PpSs震相的到时. 当叠加振幅达到最大值时,对应于最佳的地壳厚度和平均波速比.当地震台站位于沉积盆地时,接收函数会出现直达P 波能量较弱、几乎观测不到、但紧随其后的震相具有较大振幅的情况(Owens and Crosson,1988). 这种初至延迟的现象与台站下方浅层界面产生的Ps 转换波与直达P 波发生干涉有关. 基于接收函数正演计算,可建立初至延迟与沉积层厚度之间的对应关系. 利用该经验关系,通过接收函数初至延迟可大致估算沉积层厚度. 如罗艳等(2008)与Wang 和Wu 等(2017),分别给出了首都圈地区和青藏高原东北缘地区沉积层厚度的分布情况.值得注意的是,初至延迟与沉积层厚度之间的对应关系,还受其他参数的影响,如沉积层内的地震波速度. 因此在不同研究中,这种定量对应关系存有一定差异(罗艳等, 2008; Wang W L et al., 2017).
为有效约束盆地内沉积层和地壳的结构,在接收函数H
-κ
研究的基础上,Garret 等(2012) 和Yeck 等(2013)发展了序贯H
-κ
叠加扫描法. 该方法首先对台站下方的高频接收函数进行H
-κ
叠加获得沉积层厚度. 以此为先验信息,然后对低频接收函数再次进行H
-κ
扫描法,求取地壳厚度与波速比. 也有学者提出了改进的迭代H
-κ
叠加扫描法(Zhang and Huang, 2019). 当沉积层与下覆基岩存在明显的速度差、且沉积层较薄时,利用上述方法可有效约束沉积层厚度(Yeck et al., 2013).然而,较厚的沉积覆盖往往产生多次波混响,干扰甚至掩盖接收函数中Moho 界面的转换波和多次波震相,会导致H
-κ
叠加方法失效. 为消除这种混响效应,前人提出构建共振滤波器(Yu et al.,2015). 利用共振滤波器对频率域的接收函数进行滤波,然后再反变换到时间域. 该方法主要是利用了沉积层内多次波具有能量强和一定周期性的特征(Yu et al., 2015). 为减少接收函数在时频率转换中的不稳定性问题,朱洪翔等(2018)采用预测反褶积法来构建共振滤波器. 该方法具有参数设定简单、运算量小、振幅值较大等特点. 但在接收函数波形较复杂的情况下,利用共振滤波器来压制和消除沉积层多次波混响效应具有一定的困难.其次,接收函数波形包含沉积层结构信息,因此可通过波形反演方法来约束沉积层和地壳结构(图2)(Shibutani et al., 1996; Clitheroe et al.,2000; Zheng et al., 2005; 武岩等, 2014; Saikia S et al.,2016). 前人已开展大量的接收函数反演研究,采用的反演方法主要有遗传算法(Shibutani et al.,1996; Clitheroe et al., 2000)、自适应全局混合算法(Zheng et al., 2005)以及相邻算法(Saikia et al.,2016; 武岩等, 2014)等. 反演中,模型参数主要为各层的厚度、S 波速度以及V
/V
比值等. 但不同反演研究设定的模型层数并不相同. 如一些研究采用简单的沉积层和地壳双层模型(武岩等,2014).另一些研究采用了复杂模型,如Clitheroe 等(2000)设定的模型由沉积层、基底、上、中、下地壳和上地幔构成. 还有研究把沉积层细分为5 个水平层(Zheng et al., 2005). 模型参数的增加,不仅会增加计算量,而且反演结果的非唯一性问题也会更加突出. 因此当模型参数较多时,考虑到计算量、唯一性和稳定性问题,常对较小时窗范围内(如前~10 s)的接收函数进行波形反演(Clitheroe et al., 2000; Zheng et al., 2005).此外,如果非固结沉积层较厚、速度低以及与下方基岩具有较大波阻抗时,远震波场中沉积层内产生的转换波/多次波振幅会放大,可能是深部壳幔界面Ps 转换波振幅的10~20 倍. 在此情况下,垂向分量难以近似为仪器响应和有效震源时间函数的褶积. 这给常规接收函数研究带来一定挑战. 为此,Langston(2011)提出将附近基岩台站垂向分量近似为入射P 波震源函数,经过反褶积计算获得盆地内台站的垂向和径向转换函数. 然后对沉积层模型参数进行网格搜索,通过转换函数波形拟合方法获取最佳的速度结构. 由于初始模型的准确性直接影响波形拟合的计算工作量,因此在沉积层厚度给定的情况下,仅对S 波速度进行网格搜索(Langston,2011).
1.2 H-β 网格搜索法和地下接收函数
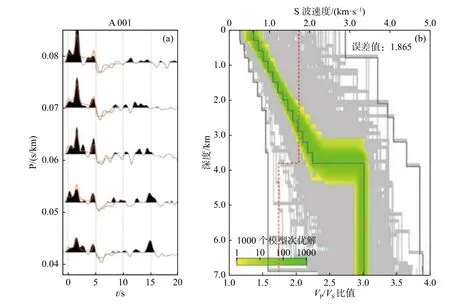
图 2 (a)利用相邻算法获得的A001 台站的接收函数波形拟合结果. 黑色为实际波形,红色为理论地震图.(b)最优的S波速度模型与波速比(修改自武岩等,2014)Fig. 2 (a) Comparison of receiver functions at A001 station between the observations (black lines) and synthetics (red lines) derived from neighborhood algorithm inversion. (b) The best fitting S wave velocity model together with VP/VS ratio (modified from Wu et al., 2014)
为有效压制接收函数中沉积层的多次振荡,Tao 等(2014)提出基于波场反延拓的H
-β
网格搜索法. 与构建共振滤波器对接收函数进行滤波处理有所不同,该方法是通过对远震波场的延拓和分解来获取沉积层和地壳结构. 下面简要介绍H
-β
网格搜索法基本原理(图3). 对水平均匀层状模型而言(如双层地壳覆盖均匀半空间地幔),远震P 波及其尾波可用水平层介质对近垂直入射的平面P 波的结构响应来表示. 在理论地震图计算中,径向和垂向分量构成P-SV 型运动方程. 以υ、υ表示速度的径向和垂向分量,τ
和τ
表示应力的径向和垂向分量,深度z
处的速度-应力向量为: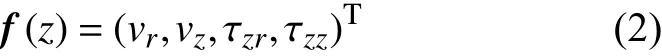
z
和z
处的速度-应力向量之间的关系可用4×4 的传播矩阵P
(z
,z
)来表示. 以此类推,深度z
处的速度-应力向量可由地表记录来表示:
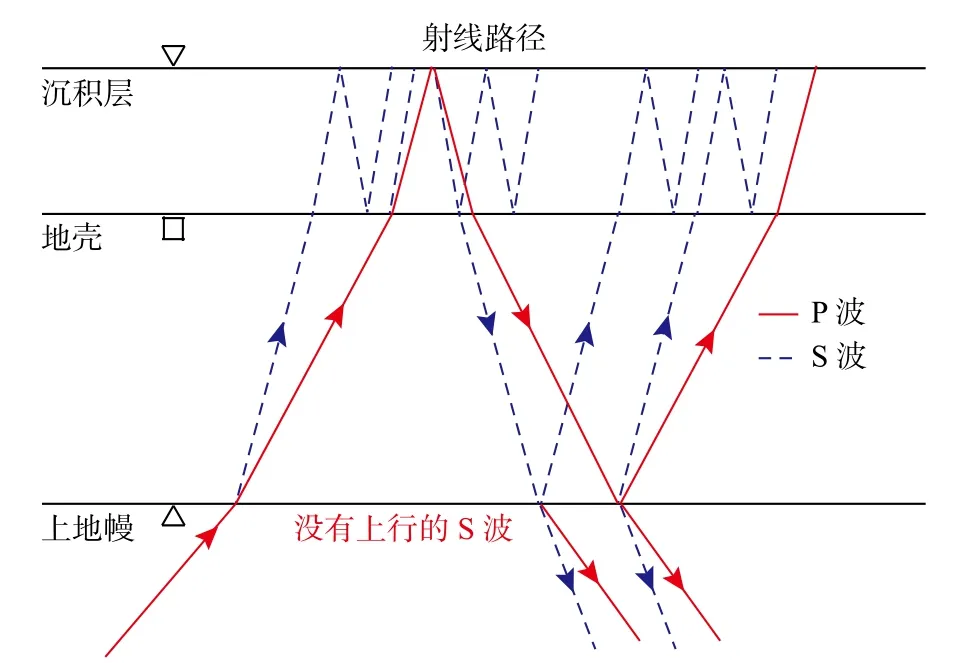
图 3 沉积盆地台站下方射线路径示意图,其中实线表示上行和下行 P 波,虚线表示上行和下行 S 波(修改自Tao et al., 2014)Fig. 3 Schematic ray paths of the upgoing and downgoing P(solid lines) and S (dashed lines) waves inside the sediment, crust and mantle in response to an incoming P wave at teleseismic distance (modified from Tao et al.,2014)
式中,f
为地表处的速度-应力向量. 由(3)式可知,由地表记录可求得任意深度处的速度和应力向量. 同时,采用弹性波场分解的方法(Kennett et al.,1978),任一深度z
处的速度-应力向量可表示为上行和下行P 波与S 波的合成: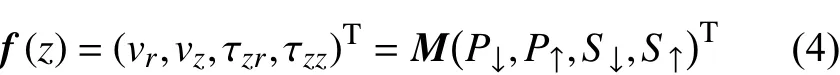
P
,P
,S
,S
)为速度-应力向量对应的上行和下行P 波与S 波的分解系数,M
是传播矩阵P
对应的特征值矩阵 .由上可知,通过波场延拓和分解方法,可将地表波形记录反传至沉积层/地壳底部,并可获得各层上行和下行P 波与S 波. 然后,基于上地幔顶部上行S 波能量最小化的准则(图3),对一定的模型参数进行网格搜索,可求取沉积层/地壳对应的最佳厚度(H
)和速度(β
).另一方面,对盆地台站而言,如果沉积层结构已知,通过波场延拓可将大量远震地表记录反传至基岩地壳,并进行上行和下行P 波与S 波的分解.然后,通过对基岩顶部上行S 波和上行P 波进行反褶积计算,可得到地下接收函数(Tao et al., 2014).已有研究显示,地下接收函数能够清晰地显示出Moho 面的转换波震相,有效改善了盆地内常规接收函数H
-κ
叠加结果(Tao et al., 2014; 况春利等,2022). 同时,利用地下接收函数可对沉积层速度结构的准确性进行评估. 如,李国良等(2019)利用背景噪声反演构建了松辽盆地沉积层速度结构模型. 利用该速度模型,计算了台站下方地下接收函数,发现沉积层震荡已基本消除,这为浅层速度结构反演的可靠性提供了有力的支持.1.3 远震P 波质点运动
当沉积盆地台站下方近地表速度低时,远震直达P 波在垂向和径向分量上会出现一定的到时延迟(简称AP 分裂),表现为随频率变化的非线性质点运动(Bao and Niu, 2017; Yang and Niu, 2019),与地震波各向异性引起的横波分裂具有一定相似性(图4). 这种频率相依赖的AP 分裂主要是由直达P 波与沉积层内的Ps 转换波叠加所致,因此通过AP 分裂时间可以约束沉积层厚度和速度.
对于远震事件,采用互相关方法可拾取不同频率下的AP 分裂时间. 然后,通过P 波实际波形与理论地震图的拟合,基于网格搜索的方法来获取近地表的S 波速度结构. 但与波场反延拓H
-β
搜索方法不同,远震P 波AP 分裂时间的网格搜索法中,需给定地壳和半空间地幔模型,仅对一定范围内的沉积层厚度和S 波速度进行搜索. 现有理论测试表明(Bao and Niu, 2017),在沉积层较薄的情况下,即使给定的P 波速度模型存在10%的偏差,基于频率依赖的AP 分裂时间仍可较好地约束沉积层结构. 然而,当沉积层较厚时,AP 分裂时间对沉积层厚度并不敏感. 造成这种情况的原因可能与近地表具有较复杂的浅层结构有关.其次,通过远震P 波/S 波的偏振分析也可直接估测近地表的速度(Park and Ishii, 2018; Park et al.,2019). P 波极化方向对S 波速度敏感,研究表明,而S 波极化方向对P 波和S 波速度均敏感. 一般常通过P 波偏振分析获取近地表的S 波速度结构. 所用的方法主要为主成分分析(principle component analysis, PCA)方法,即通过垂向和径向分量的协方差矩阵法来进行体波的偏振分析:
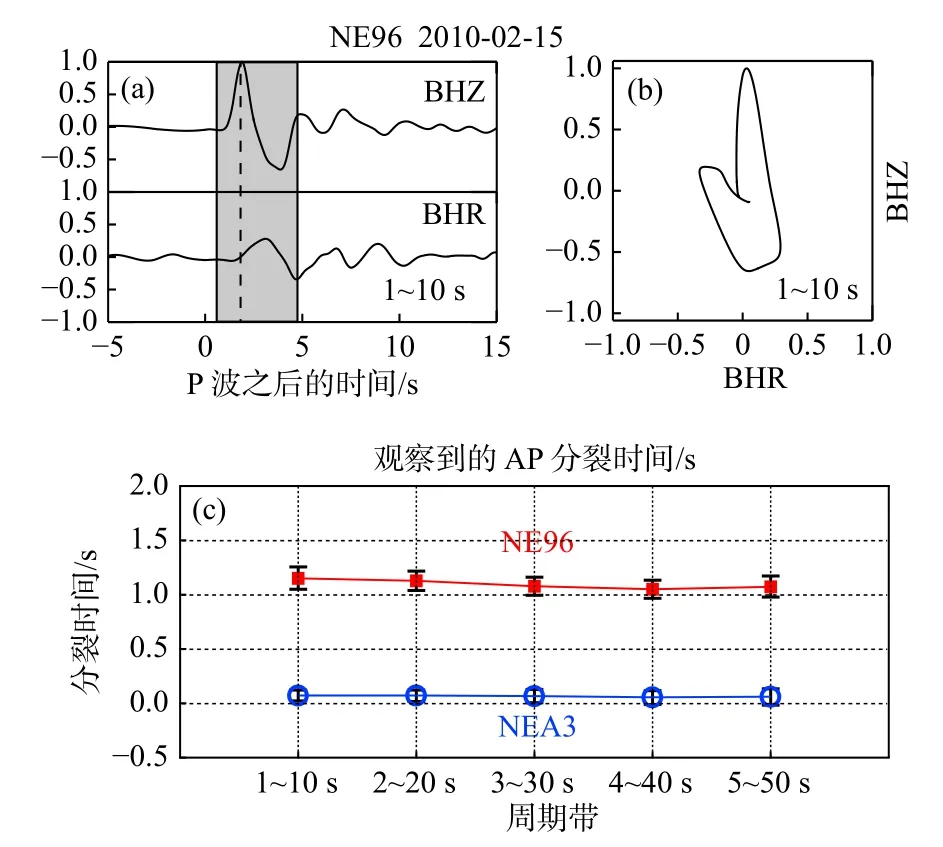
图 4 (a)NE96 台站记录到的2010 年2 月15 日发生的远震事件的垂向和径向分量,经过1~10 s 的带通滤波后的波形示意图.(b)P 波质点运动轨迹图,时窗范围见图(a)所示.(c)位于盆地内NE96 台站(红色正方形)和基岩上方NEA3 台站(蓝色圆圈,位于)测得的不同周期下的平均AP 分裂时间(修改自Bao and Niu, 2017)Fig. 4 (a) Normalized vertical-(BHZ) and radial-component(BHR) recordings of NE96 from a teleseismic earthquake occurring on 15 February 2010, which is filtered in the period band of 1~10 s. (b) The particle motion of the P wave, which is denoted by the shaded time window in Fig. 4a. (c) Comparison of the average AP splitting times as a function of period measured at NE96 (red solid squares) and NEA3 stations (open blue circles),which are deployed on sediment and bedrock, respectively (modified from Bao and Niu, 2017)
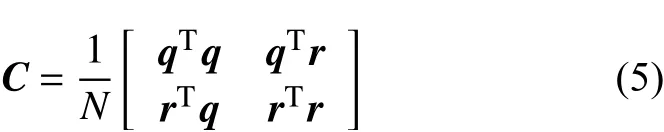
q
=[q
,…,q
]和r
=[r
,…,r
]分别表示垂向和径向时间序列.需要指出的是,协方差矩阵法的计算与地震波选取的时窗大小有关. 如果选取的时窗范围较大,包含了直达波后的Ps 转换,会直接影响P 波的质点运动,表现为明显的非线性. 其次,如前所述,P 波偏振分析具有明显的频率依赖性,如利用5~10 Hz 的高频数据可获取近地表10 m 到几百米内的速度结构,而低频数据(~0.1 Hz)适用于上地壳和深部结构的探测研究(Park et al., 2019).
2 近震体波波形方法
前人理论测试研究表明,当近地表速度很低,地震发生在速度较高的结晶基底时,近震P(S)波在台站下方近垂直入射,可近似为平面波入射( 图 5)( Langston, 2003; Chiu and Langston,2011). 在此情况下,可利用结晶基底产生的换转波和多次波的振幅与到时信息来约束沉积层结构( Chen et al., 1996; Langston, 2003; Chiu and Langston, 2011; Ni et al., 2014; Bao et al., 2021). 如,Langston(2003)利用2000—2001 年期间新马德里地震带发生的数个小震(1.7~2.4 级)事件,采用近震波形拟合的方法,对密西西比湾下方沉积层内的V
/V
比值进行了估测. 结果显示,沉积层顶部具有较高的V
/V
值(5.0),而底部的V
/V
值要小(约为2.4). Chiu 和Langston(2011)采用奇异值分解方法(SVD),对近震高频的P 波和S波波形进行联合反演,得到了新马德里地震带近地表(7 m 之内的)的1D 速度结构. 研究表明,近地表的V
和V
要低,对应的速度范围分别为0.14~0.47 km/s 和0.095~0.215 km/s. Ni 等(2014)尝试利用近震P 波的R
/Z
振幅比来约束近地表的S波速度. 马海超等(2020)对深源近震事件进行高通滤波(0.05~2 Hz),利用Ps 与P 波初至的振幅比与走时差获得了松辽盆地下方的沉积层结构.在实际应用过程中,R
/Z
振幅比需要在一个很小的时窗范围内进行测量,因而获得到的S 波速度是从地表到一定深度范围内的平均值. 这个深度范围与S 波波长有关(Li et al., 2014; Ni et al., 2014). 近震R
/Z
振幅比研究的局限性在于,为尽可能消除震源的影响,常需选取深源地震事件来满足高频近垂直入射的要求.其次,借鉴远震接收函数研究思想,有研究提出利用中等强度的近震事件,通过对径向和垂向分量反褶积,计算近震接收函数(Ni et al., 2014; 郑德高等, 2014). 同一台站下方,不同中强近震事件计算的接收函数具有很好的相似性,表明P 波初至主要与结构有关,而对地震的位置和深度并不敏感. 因此,基于近震接收函数波形拟合,可获取沉积层最优模型(Ni et al., 2014; 郑德高等, 2014).
与中强近震事件不同,对沉积盆地内台站记录到的小震近震事件,可直接通过结晶基底产生的转换波(Ps/Sp)与直达波(P/S)之间的到时差来约束台站下方的沉积层厚度(Chen et al., 1996; Bao et al., 2021). 如Bao 等(2021)利用2017 年1 月至3 月唐山地区加密流动台站观测(包含145 个台站,台间距1~4 km),选取震源深度大于10 km 的25个小震近震事件(震级在0.1~2.4 之间),通过人工拾取直达P/S 波和Ps/Sp 转换波的到时,得到了每个台站下方的S-Sp 与P-Ps 的到时差. 在V
和V
/V
给定的情况下,可进一步获得整个研究区的沉积层厚度分布图. 上述研究中转换波震相走时的拾取较为关键,仅在沉积层与下方基岩存在较大的速度差,产生的转换波震相具有较大振幅,才易于人工拾取.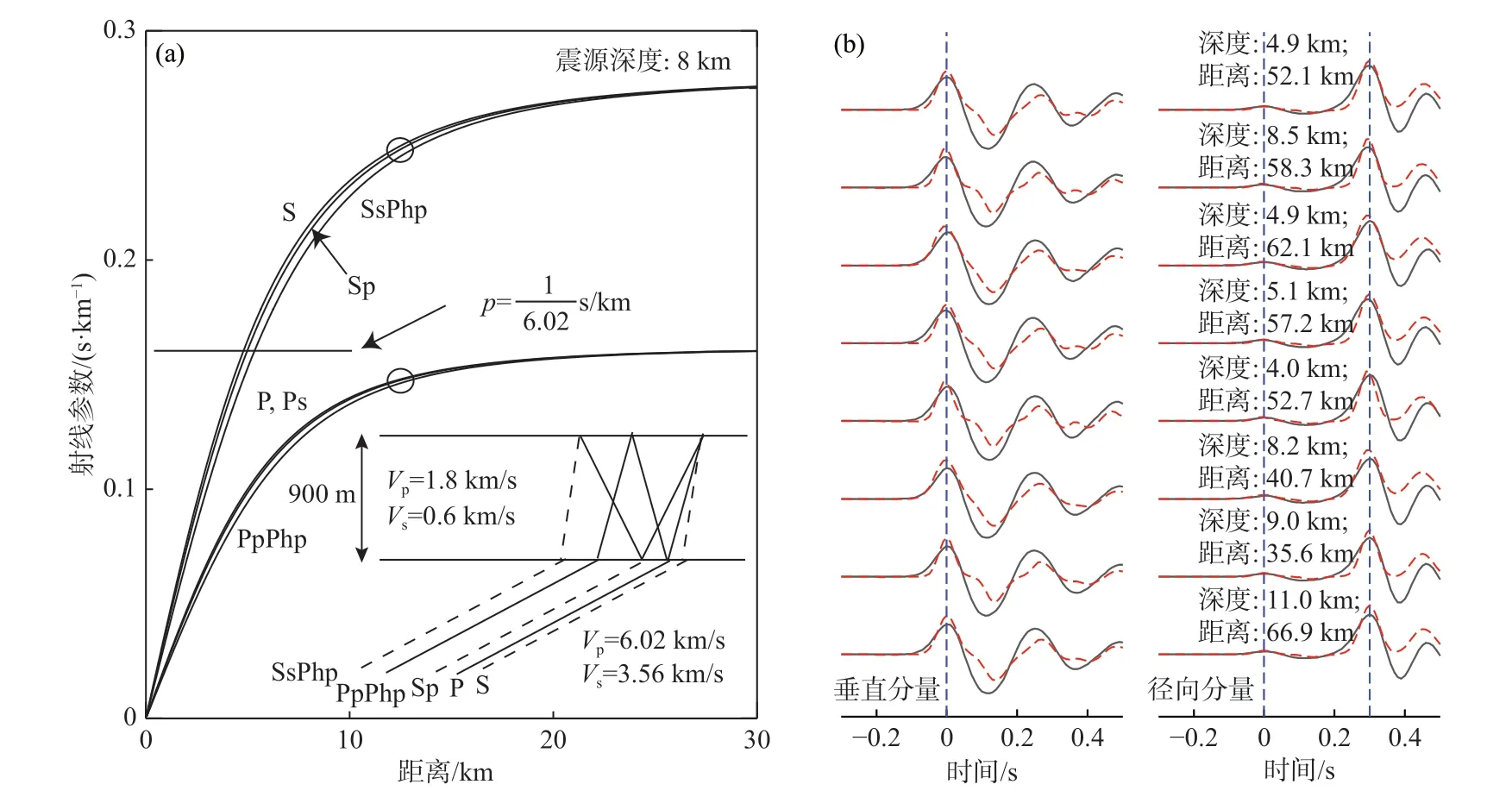
图 5 (a)从震源(8 km 深度)出发的P 波和S 波系列震相的射线参数随震中距变化图. 其中,两个圆圈表示PEBM 台站记录到的地震事件6 的P 波和S 波的射线参数,水平线表示S 波在基底处发生相移的临界射线参数(修改自Langston, 2003). (b)f–k 方法计算的爆炸源(黑线)和平面波(虚线)的理论地震图的比较,其中震源深度和震中距在径向分量中已标识(修改自Ni et al., 2014)Fig. 5 (a) Ray parameter versus distance curve for incident P and S phases from a source at 8-km depth. The two open circles show P and S ray parameters for event 6 at PEBM. The horizontal line shows the critical ray parameter where S phases undergo a phase shift due to a complex transmission coefficient at the basement boundary (modified from Langston, 2003). (b) Comparisons of the waveforms computed by f–k with explosion source (black lines) and plane-wave synthetics (dashed lines). The focal depth and epicentral distance used in the f–k computations are labeled above each radial waveform (modified from Ni et al., 2014)
3 谱比法
H
/V
(又称HVSR 或QRT)谱比法指的是地脉动水平分量(V
)与垂直分量(H
)的频谱比. 不考虑基岩放大效应和面波能量的情况下,地脉动主要是由松散沉积内的反射S 波组成. 当沉积层与基岩之间具有明显的波阻抗比时,H
/V
谱比的峰值频率与沉积层的S 波基阶共振频率(卓越频率)具有一定的对应性,因此可用来估计场地的卓越频域和放大因子 .对水平层状的沉积层-地壳双层模型而言,H
/V
基阶共振频率与沉积层厚度和平均剪切波速度有关(Carcione et al., 2017). 结合钻孔资料给出的S 波速度结构信息,可建立共振频率与沉积层厚度之间的统计关系(Ibs-Von Seht and Wohlenberg,1999). 然而这种经验关系在不同地区存有一定差异. 如,中国三河—平谷地区,沉积厚度(h
)-共振 频 率(f
) 之 间 的 关 系 式 为h
=(94.76045±8.4167)f
(彭菲等,2020). 但中国喀什乌恰地区,该经验关系式为h
=43.53f
(李文倩等,2019).H
/V
谱比法不仅可利用地脉动连续记录进行研究,也可推广应用于地震记录(Bonilla et al., 1997). 此外,与基阶共振频率仅利用单个频率信息不同,通过H
/V
谱比曲线的拟合也可用来直接反演地下介质结构(秦彤威等,2021b).与H
/V
谱比法类似,V
/H
谱比法是基于地脉动的垂直分量与水平分量的频谱比(Mostafanejad and Langston, 2017),获得的是场地P 波共振频率信息. 通常情况下,V
/H
谱比法中共振频率的峰值比H
/V
谱比法的要大,更容易识别. 但当沉积较薄时,V
/H
谱比曲线中会出现多个峰值的现象(图6),这给共振频率的选取带来较大的不确定性. 因此基于V
/H
谱比法难以建立沉积层厚度与P 波速度之间的确定关系.对于人口稠密、主动源难以开展的城市地区,地脉动H
/V
谱比法是快速评估场地作用和获取浅层结构的有效途径. 与其它方法相比,它具有简单、经济和抗强干扰的优势(Nakamura, 1989; Ibs-Von Seht and Wohlenberg, 1999; 王伟君等, 2011; 王未来等, 2011; 秦彤威等, 2021b). 但H
/V
谱比法记录的主要能量成分是体波(Nakamura, 1989; Herak, 2008)还是Rayleigh 波(Lachet and Bard, 1994; Bonnefoy-Claudet et al., 2006)仍存在争议.4 背景噪声面波成像、Rayleigh 波Z/H幅度比和多种方法的联合反演
自从Weaver(2001)等发现通过互相关技术可以从噪声中提取格林函数后,背景噪声成像研究得到了快速发展和广泛应用(Shapiro et al., 2005;Yao et al., 2006; 房立华等, 2009; Pan, 2012; Lin et al., 2013; Li et al., 2014; 李国良, 2016; 王仁涛等,2019; Wang et al., 2020; 李奇等, 2021). 与地震事件相比,利用背景噪声资料可提取台站间较短周期的Rayleigh 波格林函数. 受地球背景噪声频率谱和台间距的限制,常规噪声互相关法提取到Rayleigh波最小周期为~7 s,对地下~10 km 深度附近的速度结构比较敏感(李国良,2016).
加密流动台阵观测为浅层速度结构约束提供了有力的数据支持(Lin et al., 2013; Li et al., 2016;Wang, Lin et al., 2017; 张明辉等, 2020). 如,2011年美国Long Beach 开展了密集流动台阵观测,布设了5 200 个高频地震仪(10 Hz),台间距仅~100 m.利用该台阵的连续观测记录,Lin 等(2013)采用背景噪声互相关技术提取到了Rayleigh 波0.5~4 s的相速度频散曲线. 近年来,基于密集流动台站的背景噪声成像已成为沉积盆地和断裂带精细结构探测研究中的重要手段(Li et al., 2016; Wang Y et al.,2017; 付媛媛和肖卓, 2020). 如Li 等(2016)在合肥市区(5 km×7 km)布设了17 个流动台站,台间距约1~2 km,采用互相关技术提取到周期为0.5~2 s 的Rayleigh 波频散曲线,通过面波反演获得了近地表400 m 深度范围内的S 波速度结构. 也有学者尝试利用区域流动台阵记录提取较短周期的面波频散曲线. 如王仁涛等(2019)利用松辽盆地布设的NECESSArray 台阵垂向连续记录,采用多重滤波方法(Herrmann, 2013)提取2~14 s 的Rayleigh 波频散曲线,反演获得了盆地下方地表至12 km 深度范围内的三维S 波速度结构.
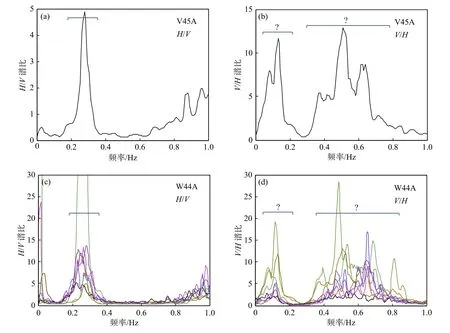
图 6 V45A 台站(沉积层厚度为869 m)得到的H/V 谱比曲线(a)和V/H 谱比曲线(b),括号表示最大峰值频率区域.W44A 台站记录到的8 个地震事件得到的的H/V 谱比曲线(c)和V/H 谱比曲线(d). 其中,H/V 谱的最大峰值共振频率为0.2~0.4,但V/H 谱的最大峰值共振频率较为复杂(修改自Mostafanejad and Langston, 2017)Fig. 6 (a) H/V and (b) V/H power spectral ratios for observed teleseismic P waves at station V45A with sediment thickness of 869 m.Brackets point out the areas of maximum peak frequency. (c) H/V and (d) V/H power spectral ratio for station W44A with overlying spectra of eight different teleseismic P waves. Brackets show the frequency band that the peak resonance may be in.Although maximum peak resonance frequency for H/V spectra is definitely arriving on 0.2~0.4, it is more complicated to recognize where maximum peak occurs for V/H spectra (modified from Mostafanejad and Langston, 2017)
除相速度和群速度外,利用Rayleigh 波的Z
/H
幅度比(瑞利波椭圆率)可对地球结构提供独立约束. 与Rayleigh 波相速度相比,Z
/H
幅度比对浅层速度结构更为敏感(Boore and Toksöz, 1969;鲁来玉, 2021; 秦彤威等, 2021a). 如周期为8 s 的Rayleigh 波的最大敏感深度在~10 km,但同周期Z
/H
幅度比的敏感深度明显要浅(李国良,2019).通过Rayleigh 波Z
/H
幅度比可约束沉积层厚度. 如曹佳俊等(2022)利用35 个地震仪组成的流动台阵观测数据,采用Rayleigh 波Z
/H
幅度比对海南琼北火山区的浅层结构进行约束. Bao 等(2018)横跨唐山断裂带,开展了台间距为1 km 的流动台站加密观测,获得了Z
/H
幅度比曲线,并基于频率—深度的转换获得了测线下方第四纪沉积结构特征.如上所述,不同的被动源探测方法对沉积层结构具有不同的分辨特性. 地球物理反演问题具有不稳定和多解性问题. 两种或多种数据集的联合反演,可以在一定程度上缓解单一方法反演的不稳定和多解性问题(Julia et al., 2000; 刘洁和张建中, 2020).因此,利用多种数据联合反演获取高分辨的沉积层结构模型是一个重要的发展趋势. 如,基于Rayleigh波Z
/H
幅度比和面波频散数据的联合反演,可对面波相(群)速度约束浅层结构进行有力补充. 袁艺等(2016)基于NA 算法将Z
/H
幅度比(25~110 s)和面波频散数据(10~150 s)进行联合反演. 还有研究采用Rayleigh 波椭圆率、相速度和远震体波波形三种数据的联合反演,开展了对松辽盆地(李国良,2016)和澳大利亚东南部沉积盆地(Li et al.,2019)结构的研究.5 松辽盆地和华北盆地沉积层结构研究进展
5.1 松辽盆地
松辽盆地位于东北地区中部,呈NNE 向菱形展布,是晚中生代以来发育的大型陆内裂陷盆地,也是我国陆相盆地中油气资源最丰富的地区. 松辽盆地广泛发育晚中生代侏罗系、白垩系和新生代沉积地层. 其中,白垩系是盆地盖层的主体. 为揭示松辽盆地油气资源构造条件和深部结构特征,前人已完成了多条地球物理测深剖面,如满洲里—绥芬河地学断面(杨宝俊等,1996),以及SinoProbe 项目在松辽盆地和周边地区布设的深反射地震剖面等(Xiong et al., 2015; 符伟等, 2019). 与此同时,盆地内开展了多项重大科学钻探工程,如位于徐家围子断陷区的“松科二井”,其钻井深达7 018 km(王璞珺等,2017;侯贺晟等,2018).
已有的剖面研究显示,松辽盆地具有典型的断陷-坳陷复合结构,其中一些局部地区沉积层厚度可达~6 km(周庆华等,2007). 同时盆地具有南北分区特征,北部断陷层上发育较厚的坳陷层向盆地边缘减薄,南部坳陷层很薄甚至缺失. 最近,松科二井附近100 km 长的深地震反射剖面也显示,测线内沉积盖层厚度为3~6.5 km(符伟等,2019).
数十年来,众多学者基于东北地区的宽频带流动台阵和区域固定台网资料,采用多种地震学手段,对松辽盆地的沉积层和地壳结构进行了研究(图7). Li 等(2016)利用NECESSArray 台阵数据,依据背景噪声互相关和地震事件分别提取到8~25 s 和10~40 s 的Z/H 振幅比,结合Rayleigh波相速度信息(Guo et al., 2015),联合反演获得了东北地区的S 波速度结构. 成像结果显示,松辽盆地南部地区的低速异常延伸到地下~3 km,而北部的异常可延伸至~6 km 深度. 这也得到了其它研究的支持. 如利用松辽盆地内42 个流动台站连续观测记录,王仁涛等(2019)采用波形互相关和多重滤波方法提取到较短周期(2~14 s)的Rayleigh波群速度和相速度频散曲线. 反演结果表明,盆地北部地区呈明显的低速异常. 如果以2.9 km/s 的S波速度对应的深度为盆地基底埋深,则中央坳陷区的沉积层厚度约3~6 km. 利用远震P 波质点运动方法,Bao 和Niu(2017)给出了松辽盆地内30 个台站下方基于不同频率的AP 分裂时间,并获得了沉积层厚度,但沉积中心位置与背景噪声成像结果(王仁涛等,2019)有所差别. 另外,Zhang 和Huang(2019)采用序贯H-κ 叠加方法,得到了盆地内24 个台站下方的沉积层厚度,整体呈现中央厚,边缘薄的形态特征. 这与采用近震P 波R/Z 振幅比和转换波震相估算的沉积层厚度分布基本相同(马海超等,2020). 最近,况春利等(2022)基于波场延拓的H-β 网格搜索法发现,松辽盆地下方存在一个速度界面,埋深在0.2~2.5 km之间. 该界面整体呈现中央坳陷区深、边缘浅、且西南地区最浅的特征, 结合深地震反射剖面研究,推测可能是坳陷层与断陷层之间界面所在深度.
5.2 华北盆地
华北盆地(也称渤海湾盆地)包括华北平原和渤海湾,是一个在太古界变质基底上发育而成的、稳定的陆相区域. 古生代华北盆地地区仍为稳定的块体,但在中、新生代经历了几个不同的裂谷和沉降阶段. 由于整个中国东部缺少古新世沉积,因此推测在这一时期普遍存在区域隆升. 最后一个裂谷阶段始于第三纪始新世,以断块、快速下沉和广泛的钙碱性玄武岩火山活动为特征(李德生, 1980;Ye et al., 1985). 活动裂谷在第三纪晚期开始减缓并逐渐下沉. 裂谷活动导致盆地内形成了一系列隆起和凹陷,包括:冀中坳陷、沧州和内黄隆起、黄骅和临清坳陷、城宁隆起和济阳坳陷(Xu et al.,1996).
大量的地震反射剖面以及钻探资料显示,该区晚第三纪-第四纪(N+Q)沉积厚度在 800~4 000 m之间,多数最深的沉积层与古新世沉积槽重合. 第三纪始新世以来的沉积厚度,在临清坳陷较薄,大约5 km,而在冀中坳陷、渤中坳陷最厚,可达7 000 m(李德生, 1980; Ye et al., 1985).
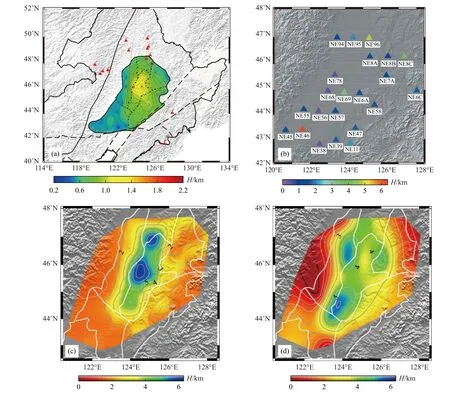
图 7 松辽盆地沉积层厚度分布图.(a)和(b)分别是利用H-β 方法(修改自况春利等,2022)和高频近震P 波转换波震相估算的沉积层厚度图(修改自马海超,2020).(c)背景噪声成像中2.9 km/s 的速度等值线对应的沉积层厚度分布图(修改自王仁涛等,2019).(d)基于频率相关的P 波质点运动方法获得的沉积层厚度分布图(修改自Bao and Niu, 2017)Fig. 7 Sediment thickness in the Songliao basin obtained by H-β method. (a) (modified from Kuang et al., 2022), and by high-frequency Ps converted from local deep earthquakes (b) (modified from Ma et al., 2020). (c) The sediment thickness at 2.9 km/s velocity isosurface obtained from short-period ambient noise tomography (modified from Wang et al., 2019). (d) The sediment thickness obtained by P-wave frequency-dependent P Wave particle motion (modified from Bao and Niu, 2017)
在过去的10~15 年中,随着首都圈数字地震台网固定地震台站和一系列流动地震观测计划的实施,对华北地区沉积层结构进行了调查研究,所用手段包括人工地震(段永红等,2016)、接收函数方法(罗艳等,2008;武岩等,2014)和P 波质点运动方法(Bao and Niu, 2017)等(图8). 如罗艳等(2008)利用首都圈数字地震台网记录,根据接收函数P 波初至延迟给出了华北地区沉积层大致厚度,结果显示首都圈地区沉积层厚度为4~7 km.武岩等(2014)利用2006~2009 年期间华北布设的宽频带流动台阵资料,采用接收函数波形模拟获得到渤海湾盆地沉积层结构. 研究认为,华北地区沉积层厚度为1~6 km,其中冀中坳陷带沉积最厚处可达3~6 km,并呈NE-SW 向展布. 这一结果得到了人工地震测深观测的支持,如段永红等(2016)利用华北地区人工地震宽角反射、折射探测资料构建的地壳三维速度模型显示,东部地区沉积层厚度在2~6 km 之间. 同样使用华北流动台阵记录,Zhang 和Huang(2019)采用接收函数序贯H
-κ
扫描方法估测华北盆地沉积层厚度为1~6 km,但沉积较厚的凹陷带呈NW 向展布. 另外,基于华北台阵资料开展的背景噪声面波和接收函数联合反演认为,华北盆地沉积层厚度大于3 km,局部地区可达5~6 km(姜磊等,2021). 与该研究有所不同,Li 等(2021)利用区域固定台站资料,采用接收函数序贯H
-κ
扫描方法估测华北盆地沉积层厚度要薄,不超过3 km. 考虑到固定台站分布稀疏,Li 等(2021)的结果可能难以刻画研究区复杂隆起和凹陷区的沉积结构. 此外,利用华北台阵资料,Yang和Niu(2019)利用P 波质点运动方法(Bao and Niu, 2017)获得了渤海湾盆地沉积层结构,结果表明华北东部沉积层厚度在1~3.7 km 之间,这与Ye 等(1985)给出的晚第三纪—第四纪(N+Q)沉积厚度分布基本相似.6 结 论
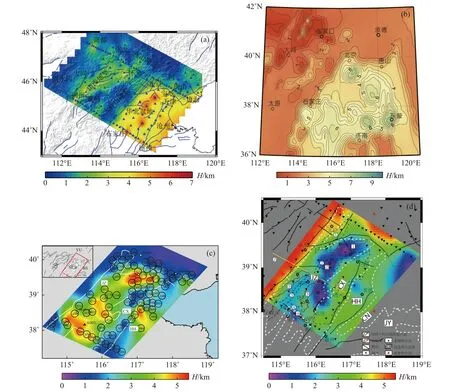
图 8 华北克拉通中部和东部地区沉积层厚度分布图. 其中(a)和(b)分别是利用背景噪声面波和接收函数联合反演方法(修改自姜磊等,2021)和采用人工地震测深(修改自段永红,2016)得到的沉积层厚度分布图. (c)和(d)分别是采用接收函数波形反演方法(修改自武岩等,2014)和序贯接收函数H-κ 扫描方法(修改自Zhang and Huang, 2019)获得的渤海地区沉积层厚度分布图Fig. 8 Sediment thickness beneath the central and eastern North China Craton, obtained by joint inversion of receiver function and Rayleigh wave dispersions (a) (modified from Jiang et al., 2021) and deep seismic sounding (b) (modified from Duan et al 2016). The sediment thickness of Bohai Bay basin derived by receiver function waveform fitting (c) (modified from Wu et al.,2014) and sequential H-κ stacking method (d) (modified from Zhang and Huang, 2019)
沉积盆地结构研究对油气资源勘探开发、防震减灾、深部结构成像与构造演化等都具有重要意义. 目前,基于被动源地震台站记录已逐渐成为沉积盆地精细结构探测的重要途径. 与主动源探测不同,被动源数据分析研究通常获得的是近地表的S波速度结构. 本文总结了基于被动源数据约束沉积层结构的一些主要地震学方法和相关进展. 其中,利用远震地震事件的方法有:接收函数和转换函数,波场反延拓的H
-β
网格搜索法、以及P 波质点运动偏振分析. 这些方法主要是利用台站下方浅层界面上产生的转换波和直达波的到时差和振幅信息来约束沉积层厚度和速度. 利用近场记录也可约束沉积层结构,但主要采用的是高频波形拟合方法. 其次,本文还简要介绍了基于地脉动和地震事件的谱比法、背景噪声面波成像,以及Rayleigh 波Z
/H
幅度比分析方法. 由于地球物理反演的不确定性,多种数据联合反演获取高分辨的沉积层结构是重要的发展趋势. 此外,尽管目前多数研究认为松辽盆地下方沉积层结构存在南北分区特征,但不同研究得到的沉积层厚度还存有差异. 同样的,已有的华北盆地沉积层厚度分布情况也存有不一致性. 综合上述研究,我们认为沉积层精细结构的探测仍然是今后地震学研究发展的一项重要挑战.附中文参考文献
曹佳俊,郭震,夏少红,等. 2022. 利用H
/V
方法研究琼北火山区的浅表层地质变化特征[J]. 热带海洋学报,41(1):10.段永红,王夫运,张先康,等. 2016. 华北克拉通中东部地壳三维速度结构模型(HBCrust1.0)[J]. 中国科学:地球科学,46(6):845-856.
房立华,吴建平,吕作勇. 2009. 华北地区基于噪声的瑞利面波群速度层析成像[J]. 地球物理学报,52(3):663-671.
符伟,侯贺晟,高锐,等. 2019. “松科二井”邻域岩石圈精细结构特征及动力学环境——深地震反射剖面的揭示[J]. 地球物理学报,62(4):1349-1361.
付媛媛,肖卓. 2020. 青藏高原东北缘及邻区Rayleigh 和Love 波背景噪声层析成像[J]. 地球物理学报,63(3):860-870.
侯贺晟,王成善,张交东,等. 2018. 松辽盆地大陆深部科学钻探地球科学研究进展[J]. 中国地质,45(4):641-657.
姜磊,丁志峰,高天扬,黄翔. 2021. 利用背景噪声和接收函数研究华北克拉通地壳结构[J]. 地球物理学报,64(5):1585-1596.
况春利,张瑞青,陈成峰,刘嘉栋. 2022. 松辽盆地地壳精细结构研究[J]. 地震学报,44(4). DOI: 11939/jass.20210108.
李德生. 1980. 渤海湾及沿岸盆地的构造格局[J]. 海洋学报 (中文版),2(4):93-101.
李国良. 2016. 瑞利波椭圆率的测定与在反演S 波速度结构中的应用[D]. 北京:中国石油大学.
李国良. 2019. 利用被动源数据联合反演盆地3D 速度结构[D]. 北京:中国石油大学.
李奇,张智,侯爵,等. 2021. 背景噪声提取体波方法研究进展[J].地震科学进展,51(10):433-451.
李文倩,何金刚,朱皓清. 2019. 基于H
/V
谱比法的场地卓越频率研究[J]. 内陆地震,33(4):314-320.刘洁,张建中. 2020. 重震联合反演框架及应用新进展[J]. 地球物理学进展,35(2):743-752.
鲁来玉. 2021. 基于平面波模型重访地震背景噪声互相关及空间自相关(SPAC)[J]. 地球与行星物理论评,52(2):123-163.
罗艳,崇加军,倪四道,等. 2008. 首都圈地区莫霍面起伏及沉积层厚度[J]. 地球物理学报,51(4):1135-1145.
马海超,储日升,盛敏汉,等. 2020. 利用深源近震高频Ps 转换波震相研究松辽盆地沉积层结构[J]. 大地测量与地球动力学,40(2):214-220.
彭菲,王伟君,寇华东. 2020. 三河—平谷地区地脉动H
/V
谱比法探测:场地响应、浅层沉积结构及其反映的断层活动[J]. 地球物理学报,63(10):3775-3790.秦彤威,冯宣政,王少曈,鲁来玉. 2021. Rayleigh 波 ZH 幅度比(椭率)研究综述[J]. 地球物理学进展,36(1):39-66.
秦彤威,王少曈,冯宣政,鲁来玉. 2021. 微动 H/V 谱比方法[J]. 地球与行星物理论评,52(6):587-622.
滕龙,倪四道,李志伟. 2014. 重力测定盆地沉积层厚度的方法及其进展[J]. 地球物理学进展,29(5):2077-2083.
王海云,谢礼立. 2008. 近断层地震动模拟现状[J]. 地球科学进展,23(10):1043-1049.
王璞珺,刘海波,任延广,等. 2017. 松辽盆地白垩系大陆科学钻探“松科2 井”选址[J]. 地学前缘,24(1):216-228.
王仁涛,李志伟,包丰,等. 2019. 松辽盆地沉积层结构的短周期地震背景噪声成像研究[J]. 地球物理学报,62(9):3385-3399.
王伟君,陈棋福,齐诚,等. 2011. 利用噪声 HVSR 方法探测近地表结构的可能性和局限性——以保定地区为例[J]. 地球物理学报,54(7):1783-1797.
王未来,吴建平,房立华. 2011. 利用地脉动信息约束沉积层区域台站下方速度结构反演[J]. 地震学报,33(1):28-38.
武岩,丁志峰,朱露培. 2014. 利用接收函数研究渤海湾盆地沉积层结构[J]. 地震学报,36(5):837-849.
杨宝俊,穆石敏,金旭,等. 1996. 中国满洲里——绥芬河地学断面地球物理综合研究[J]. 地球物理学报,39(6):772-782.
袁艺,姚华建,秦岩. 2016. 基于邻域算法的瑞利面波垂直—水平振幅比及频散曲线联合反演及应用[J]. 地球物理学报,59(3):959-971.
张明辉,武振波,马立雪,等. 2020. 短周期密集台阵被动源地震探测技术研究进展[J]. 地球物理学进展,35(2):495-511.
郑德高,李志伟. 2014. 基于远震接收函数与近震P 波波形的沉积层结构研究[C]. 2014 年中国地球科学联合学术年会——专题6:岩石圈结构与大陆动力学论文集.
周庆华,冯子辉,门广田. 2007. 松辽盆地北部徐家围子断陷现今地温特征及其与天然气生成关系研究[J]. 中国科学 D 辑,37(增刊Ⅱ):177-188.
朱洪翔,田有,刘财,等. 2018. 沉积盆地地区地壳结构估计——预测反褶积方法消除接收函数多次波混响[J]. 地球物理学报,61(9):3664-3675.
