无人机辅助车联网的无人机部署算法
2022-08-19谢英辉彭维捷苏秀芝邱春荣杨洪朝
谢英辉彭维捷苏秀芝邱春荣杨洪朝
(1.长沙民政职业技术学院,长沙 410004;2.长沙商贸旅游学院,长沙 410001;3.湖南软件职业技术大学,湘潭 411100)
1 引 言
由于易部署、移动方便,无人机(Unmanned Aerial Vehicle,UAV)已在无线网络领域内广泛使用,其中基于UAV 的车联网(Vehicle-to-everything,V2X)是UAV 的典型应用之一。 在UAV-V2X 中,UAV 扮演空中的路边单元(Roadside Unit,RSU)。
V2X 通信中既包含了车间通信,也包含了车与基础设施间通信(Vehicle-to-Infrastructure,V2I)。 考虑到部署成本,不可能在所在道路上部署RSU。 因此,利用UAV 扮演RSU,降低了部署成本,提高了V2I 通信服务效率。
尽管UAV 存在较多优势,但它的能量消耗、低空飞行时间、三维空间部署以及回传链路(Backhaul Link,BL)等问题仍需优化。 为此,研究人员试图解决这些问题。 例如,文献[5]研究了能效的三维部署策略,并得出城市海拔高度是维持强健的UAV网络的重要参数的结论。
文献[6]处理了在紧急情况下的UAV 的能量以及回传问题,并提出利用系留式无人机(Tethered Drone,TD)克服回传问题。 然而,它们假定由TD 提供的回传链路是高速率的,这忽略了回传链路容量受约束的问题。 文献[7]也讨论了基于回传感知的UAV 部署问题,并提出基于最大化服务用户数和用户数的数据速率的UAV 部署策略,分析了用户移动对最优部署方案的影响。 此外,文献[8]考虑了数据传输时延问题,并提出基于最小化等待时间的网络模型。
为此,针对UAV-V2X 中的UAV 部署问题进行分析,构建了基于时延和回传链路的能效的UAV部署的目标函数,旨在减少UAV 总的功率消耗。
2 网络模型
考虑如图1所示的UAV-V2X 网络场景,其中UAV 扮演空中RSU,为陆地上用户构建V2I 链路。因此,UAV 可以与车辆用户(Vehicular Users,VUs)分享道路信息,并协助VUs 间的数据传输。
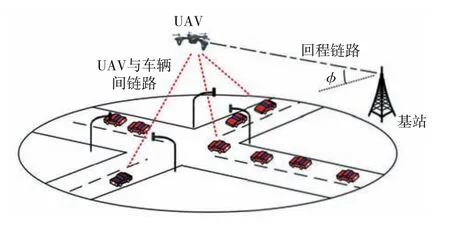
图1 UAV-V2X 的网络场景图Fig.1 Communication model of UAV-V2X
令C表示基站(Base Station,BS)与UAV 间回传链路容量。 本文的研究目的在于:在不超过链路容量C和满足时延要求的基础上,通过优化VUs的功率分配,最小化UAV 总的功率消耗。
2.1 空-地的信道模型
常用陆地信道模型不再适用于在空中飞行的UAV。 依据文献[9],可利用由视距和非视距链路产生的平均损耗率表示空-地对路径损耗模型。
为此,先推导VUs 与UAV 间的视距链路概率。假定UAV 在平面的位置坐标为(x,y),其相对地面高度为h。 假定第个VUs(U)的位置坐标为(x,y)。 用PL表示U与UAV 间链路为视距链路的概率:
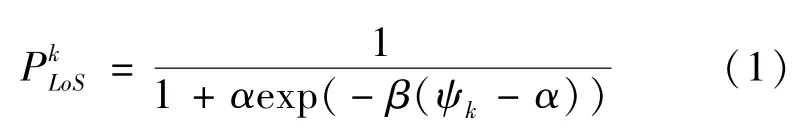
式中:,——由环境决定的参数;ψ——链路的海拔角度,ψ=arctan(h/d)。
设d为UAV 与U在二维平面间的距离,即:

再利用式(3)计算链路的路径损耗:
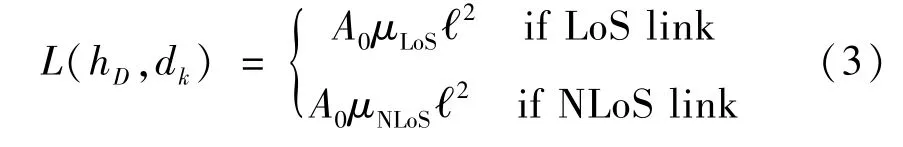
其中,

式中:,——视距和非视距链路的额外损耗;LoS,NLoS——视距和非视距链路;f——载波频率;c——光速,m/s。
最后,利用式(6)计算平均路径-损耗:
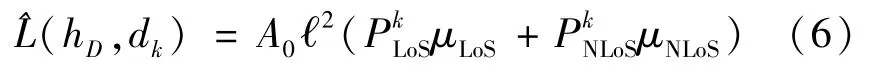
2.2 回传链路容量
假定一个UAV 为个VUs 提供数据链路服务。 这个VUs 到达UAV 的覆盖区域的过程服从泊松过程,其中UAV 的高度为h。 UAV 下行链路的天线增益为:

式中:——VUs 至UAV 上行链路的仰角;θ——下行链路天线的半功率波束宽度;≈30 000;G——其余旁瓣所获取的功率增益。
在总带宽为上采用正交频分多址(Orthogonal Frequency Division Multiple Access,OFDMA)技术。因此,利用式(8)计算VU 端所接收的信号功率:

式中:P——分配给U的功率。
利用式(9)计算下行链路数据率:
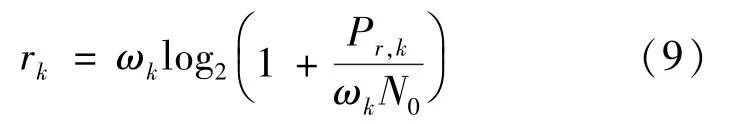
式中;ω——分配给U的子信道带宽;——零均值的高斯白噪声的功率谱密度。
由于回传链路容量不超过C,网络内所有子信道的数据率应不大于C。 因此,回传链路容量受式(10)约束:

其中,

式中:W——回传链路所需的带宽,假定W为系统已知参数;P——BS 的传输功率。
对BS 与UAV 间的路径损耗L进行dB 换算:


UAV 与BS 间的信道参数如表1所示。

表1 UAV 与BS 间的信道参数Tab.1 Parameters of the channel between UAV and BS
2.3 时延模型
时延是衡量V2X 通信网络的一个重要参数。令Q表示在时隙第个VUs(U)在缓冲区内的存储的数据包数。 令W()和δ()分别为第个数据包在缓冲区的等待时间和传输时延。 此外,U的第个数据包的时延表示为:
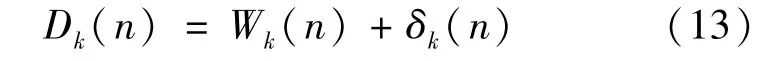
由于V2X 通信要求低的通信时延,每个VU 在缓冲区的时延应限制于某个范围内,如式(14)所示:
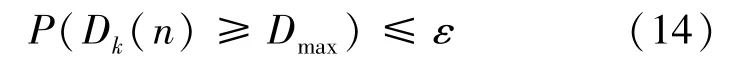
式中:——允许传输数据包的可容忍的时延,在V2X 网络中,一般=100 ms;——D()大于的概率。
2.4 功率消耗模型
假定UAV 盘旋在上空。 因此,UAV 主要有来自两个方面的功率消耗:通信和在空中盘旋。 由于UAV 采用正交信号为地面上的用户提供服务,每个子信道的通信所消耗的功率为:

为了简化表述,假定子信道数等于VUs 数。 令表示UAV 在空中盘旋所消耗的功率,其由两部分组成,如式(16)所示:
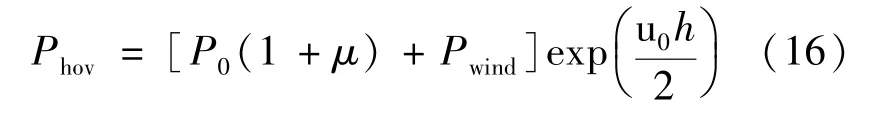
其中:
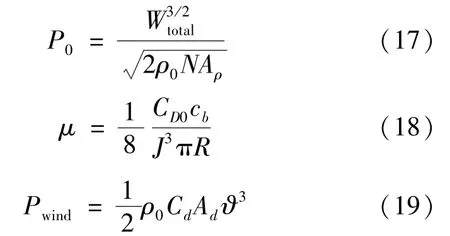
式中:——UAV 在平均海平面上的功率消耗;——附加功耗因子;——克服气流所消耗的功耗;;u——常数,且u=9.7 ×10;——海拔高度;——UAV 马达旋转时产生的推力;——在空气密度值,通常=1.225 kg/m;A——单螺旋桨所跨度的面积;C——牵引系数;c——叶片的弦长;——螺旋桨进程系数;——每螺旋桨的半径;C,A——无人机的牵引系数和车辆的正面面积;——风速,m/s。
令表示UAV 总的能量消耗,其定义如式(20)所示:
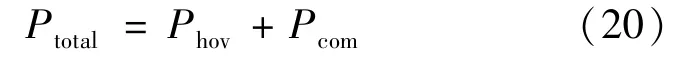
本研究目的在于最小化。 注意:1)由于电池和马达驱动器提供的功率有限,对进行限制,即≤;2)由于功率放大器受限,通信的总的传输功率也受限,即≤。
3 基于功耗最小化的目标函数及求解
3.1 目标函数
根据第1 节所建立的模型,建立目标函数。 建立目标函数的准则为:1)最小化UAV 的功率消耗;2)遵守VUs 的可容忍的时延;3)不违背回传链路容量。
根据式(16),盘旋的功率是关于高度的指数函数。 而UAV 的高度h依赖于城市的海拔高度。 因此,重新表述盘旋在地面上的高度:
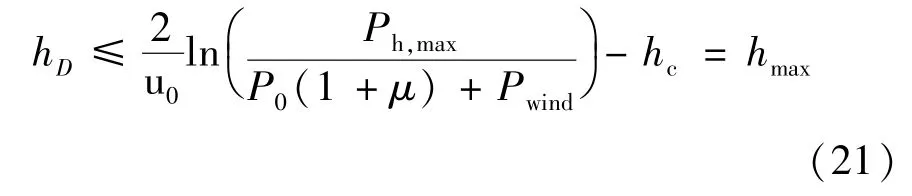
由于直接通过式(14)计算时延非常困难。 因此,将其转换成单独数据率约束条件,并采用最大代数队列算法求解。 考虑GI/GI/1 队列,对于任意一个VUs,如果它的缓冲区在时隙被一些数据占用,则瞬时速率()应大于维持容忍时延的最小速率,其定义如式(22)所示:
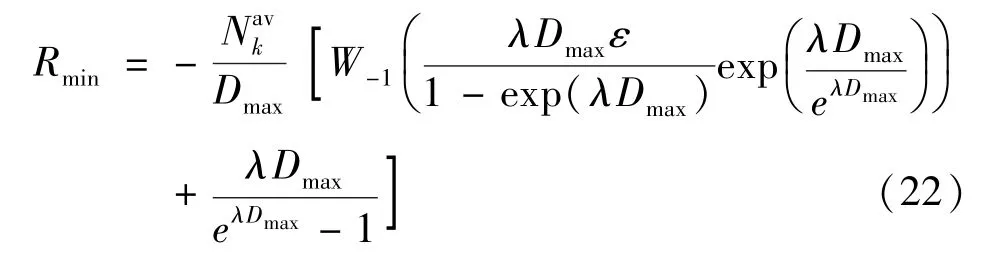

任意第个VUs 用户,端到端时延应满足:r≥。 最后,可建立目标函数为:
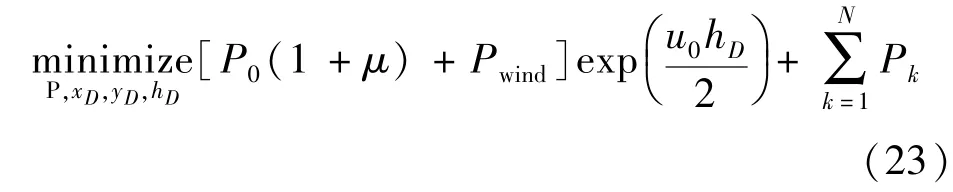
该目标函数的约束项为:
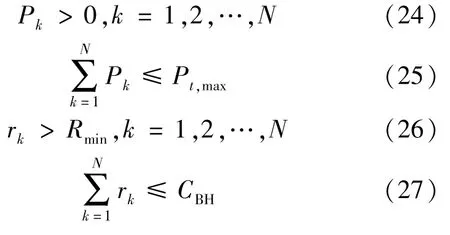
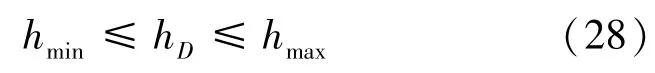
3.2 基于序列二次规划的目标函数求解
式(23)所示的目标函数为带约束非线性优化问题。 为此,利用序列二次规划(Sequential Quadratic Programming,SQP)求解目标函数。 SQP 算法具有良好的理论基础及较强的边界搜索能力,其在解决非线性约束优化问题中得到广泛应用。
4 性能分析
4.1 仿真环境
在Windows 7 操作系统、8GB 内存,core i7 CPU的PC 上进行实验仿真。 利用MATLAB 软件建立仿真平台。 仿真参数如表2所示。
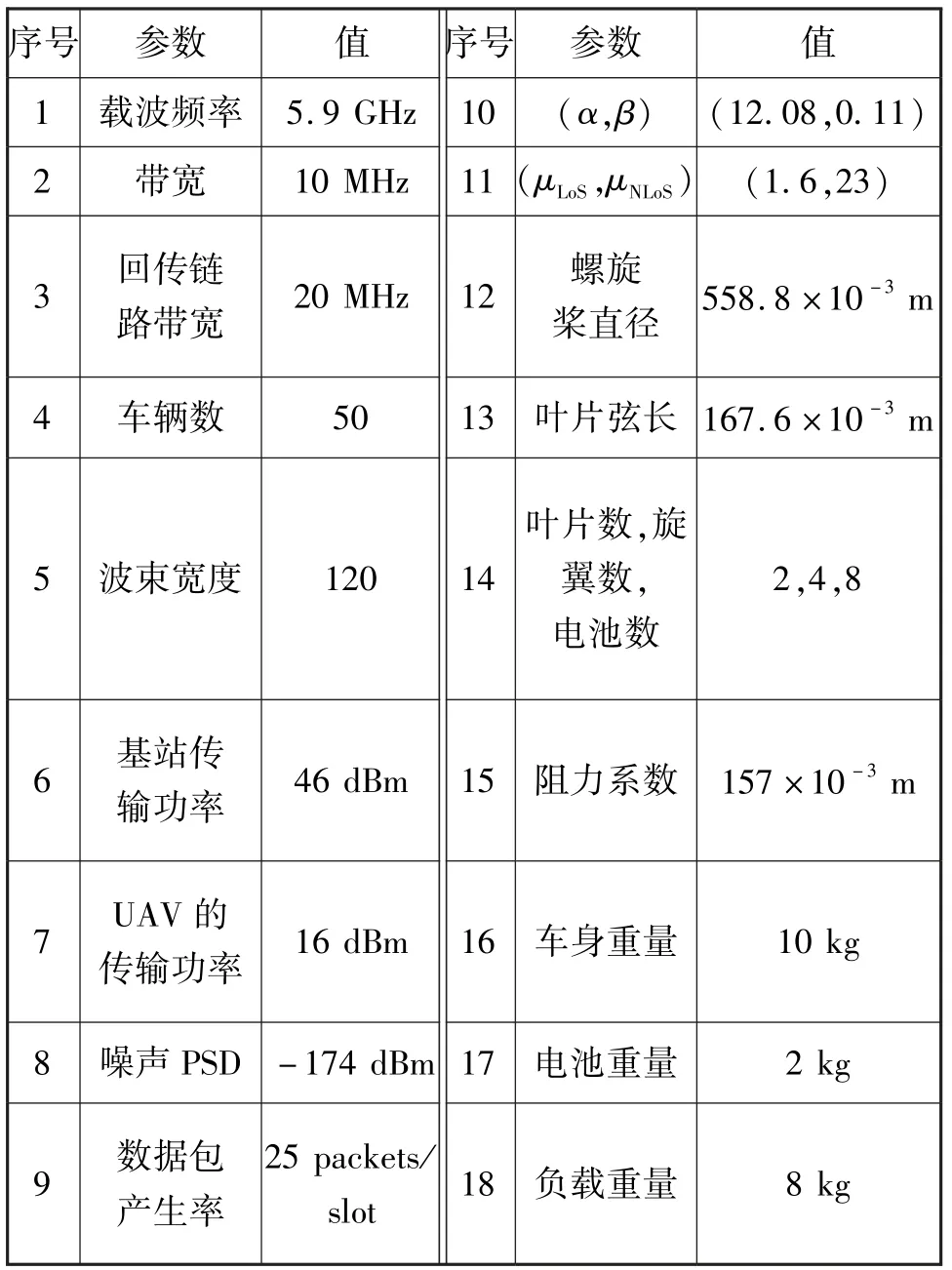
表2 仿真参数Tab.2 Simulation parameters
4.2 最小速率Rmin的性能

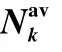
表3 最小速率Rmin随ε 和的变化情况Tab.3 Minimum data rate Rmin with ε and
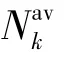
4.3 最优的UAV 高度及消耗的总功率
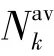

图2 最优的UAV 高度及消耗的总功率图Fig.2 Optimum height and total power consumption
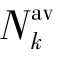
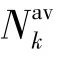
4.4 回传链路的负载
由于回传链路容量是关于UAV 与BS 间距离函数,回传链路容量不是固定的值。 为了评估链路的适应能力,引用回传链路负载指标,其等于总的VUs 速率之和与回传链路容量的比值,即=∑r/C。 对回传链路负载的影响如图3所示。
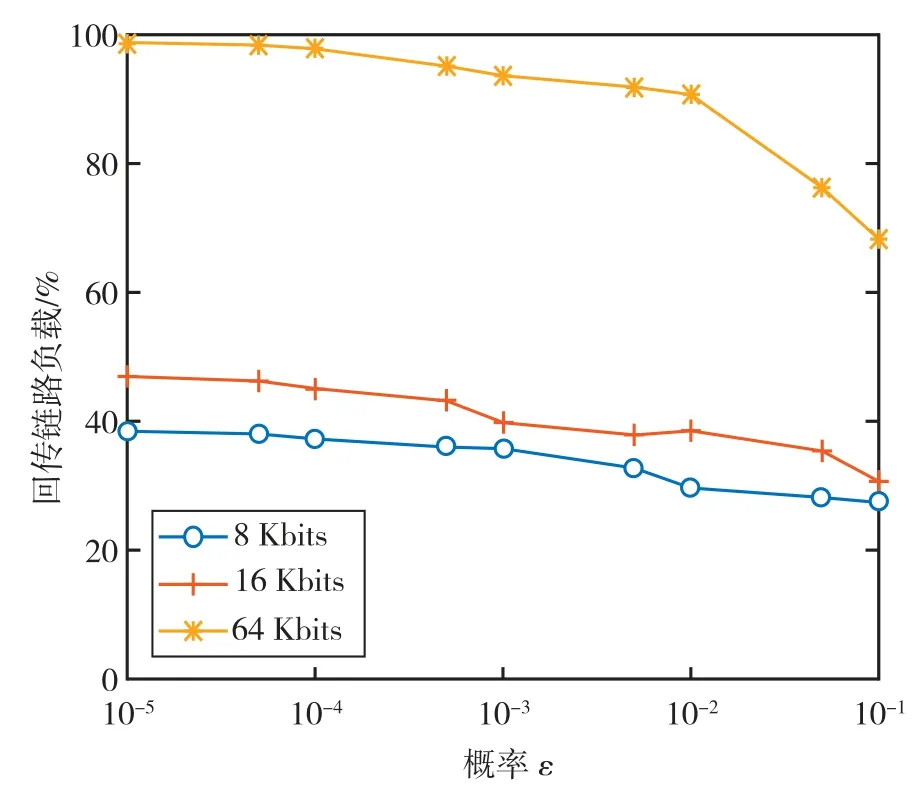
图3 回传链路负载图Fig.3 Backhaul link load

1)最小速率随增加而下降。 相应地,在时延约束条件下,所有用户总速率将小于单个速率。 这就降低了=∑r的值;
2)从图2可知,增加使UAV 高度下降,就减少了UAV 离BS 间的平面距离。 这就提升了回传链路的质量。
5 结束语
系统分析了UAV-V2X 中的UAV 部署问题。通过优化UAV 部署,在满足时延要求,并遵守回传链路容量的基础上,减少UAV 的总的功率消耗。先构建信道、回传链路、时延和功率消耗模型,然后构建目标函数,并利用SQP 求解。 性能分析表明,当平均数据包尺寸增加,UAV 与BS 间的链路负载增加。
