基于人工智能技术的雷达目标检测

王 炼董胜波

（北京遥感设备研究所，北京 100039）

1 引 言

脉冲多普勒（Pulse Doppler，PD）雷达导引头是一种利用全倒置接收机技术检测目标速度信息的全相参体制的雷达导引头，能实现对雷达信号的窄带多普勒滤波输出准连续波单谱信号，具有对目标进行速度维高分辨识别的能力，进而实现对目标的远距离检测和跟踪。

现代战争战场环境复杂多变，战争中的电磁环境越来越复杂，多种地海杂波背景并存，严重影响雷达导引头下视情况下的目标检测。

真实的雷达散射杂波特性很复杂，其动态散射特性和产生机理仍然是世界性难题，城市杂波、海杂波等复杂杂波其概率分布特性各不相同，很难统一描述，有不少学者尝试用混沌模型来阐述海杂波的散射特性，对海杂波产生的机理进行深入分析，推导出海杂波的非线性动力方程，而神经网络强大的非线性预测能力能对海杂波的非线性动力方程进行逼近，从而实现对海杂波的高维非线性预测，给强杂波背景下的小目标检测提供了新的方法。

2 雷达导引头目标检测

2.1 目标信号模型

PD 雷达导引头是一种利用全倒置接收机技术检测目标速度信息的全相参体制的雷达导引头，能实现对雷达信号的窄带多普勒滤波输出准连续波单谱信号，具有对目标进行速度维高分辨识别的能力，主要应用于杂波背景中打击运动目标的场合。

PD 信号模型如下：

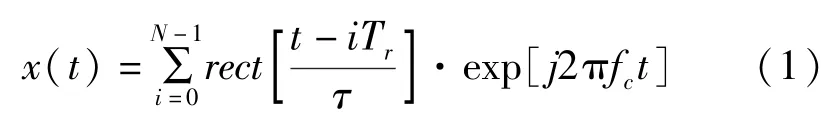
其中：

式中：——相参处理发射脉冲数；T——信号脉冲重复周期；——脉冲宽度；f——载频。

2.2 雷达信号检测原理

经典的雷达信号检测原理是基于白噪声背景下的雷达目标信号检测，检测原理图如图1所示，（）为目标回波信号，（）为匹配接收机的底噪。雷达的目标信号检测其目标就是在白噪声背景下去发现真实雷达目标，首先对匹配接收机接收到的回波信号（）进行数字抽样处理，得到离散数字序列＝｛…x｝，然后对数字序列进行相参积累滤波等处理，最后依据奈曼皮尔逊等雷达信号判决准则对真实的目标是否存在进行判决。

图1 雷达信号检测原理框图Fig.1 Block diagram of radar signal detection schematic design

2.3 PD 雷达目标检测方法

对PD 雷达导引头来说，其接收机为全倒置接收机，能对雷达目标进行多普勒域的窄带滤波，输出的信号为准连续波单谱信号，因此，对于PD 雷达导引头的目标可以看成点目标，窄带点目标满足：

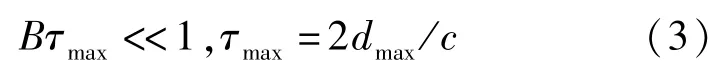
式中：——发射射频信号（）的信号带宽；——目标的最大径向长度。

则此时的目标将视为点目标，信号检测即为噪声背景下的点目标检测。

为了提高PD 雷达导引头的威力，雷达导引头在实际应用中不会只发送一个脉冲，而是发射一连串同频脉冲信号，接收机端接收到目标信号回波后，对每个脉冲进行预处理，并对预处理后的脉冲串进行相参积累滤波，其检测处理过程如下。

发射信号可以表示为：

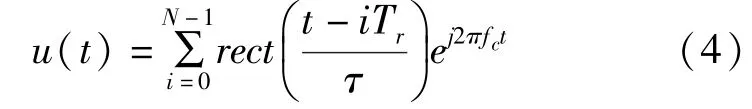
式中：T——重复周期；——脉冲宽度。

对多脉冲的相参积累检测，对PD 雷达导引头，在一个相参积累周期内，目标的运动对距离波门走动的影响可以忽略，即δ＝2＞＞vNT，此时即可用DFT 或者FFT 来实现对脉冲串的相参积累（CI），PD 雷达导引头相参积累检测器的原理框图如图2所示。

图2 PD 雷达导引头相参积累检测器原理框图Fig.2 Block diagram of PD radar seeker coherent accumulation detector

在工程实践中，对目标的速度或多普勒值无法准确预知，通常会采用一个速度指示容错能力较强的宽速度门，即多普勒滤波器组对目标回波信号进行滤波，如图2所示目标回波信号先经过单脉冲匹配滤波，为了提高导引头的威力，还需要对脉冲串进行全相参积累处理，最后进行判决。

3 人工智能技术

随着智能信息处理技术的发展，人工神经网络在信息处理领域得到的飞快的发展，现在人工神经网络技术已经广泛应用在图像处理、模式聚类识别和高维非线性预测等方向，人工神经网络的强大主要体现在其学习和泛化能力上，人工神经网络通过对有限的样本进行反复训练和学习，在学习和训练过程中不断进行修正和改善，以掌握隐含在有限样本中的内在规律。

基于BP 算法的多层前馈神经网络技术在高维非线性预测、图像处理、目标识别等方向有独特优势。 其学习和训练过程由信号的正向传播与误差的方向传播两个过程组成。

设输入向量＝（，，…，x），中间层输出向量为＝（，，…，y），输出向量为＝（，，…，a），输入层到中间层之间的权值向量为＝（，，…，v），中间层到输出层间的权值向量为＝（，，…，w），构建一个三层BP 人工神经网络，其组成示意图如图3所示。

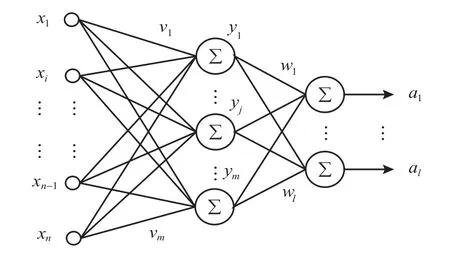
图3 三层BP 人工神经网络示意图Fig.3 Sketch map of three-layer BP neural network show

BP 学习算法中，各层权值调整形式上是一致的，均由学习速度、本层的输出误差及本层输入信号3 个因素决定。

4 强杂波背景下的PD 雷达导引头小目标检测

海杂波会严重影响导引头的目标检测，且均与目标信号有一定相关性的非高斯统计特性。 对强海杂波等非高斯背景下的小目标检测，可以利用杂波与真实目标信号的频率差，在相邻CPI 周期间，杂波可以视为不变的，而目标是运动的，对目标回波信号进行杂波对消滤波，对消滤波后的残差服从高斯分布，然后运用高斯噪声背景下的经典目标检测理论进行目标检测。 利用BP 神经网络的强大非线性预测功能对海杂波进行预测对消，对强海杂波背景下的PD 雷达导引头小目标检测转化为高斯噪声背景下的导引头小目标检测。

4.1 基于BP 神经网络的非线性方程的预测

神经网络理论中著名的柯尔莫哥洛夫（Kolmogorov）连续性定理是神经网络对高阶非线性方程逼近的理论基础，令（）为有界单调递增的一元连续函数，（） ＝（，，…，x）为连续实值函数，对于任意的＞0，存在正整数和实数c，b（＝1，2…，）及w（，＝1，2…，），使得：

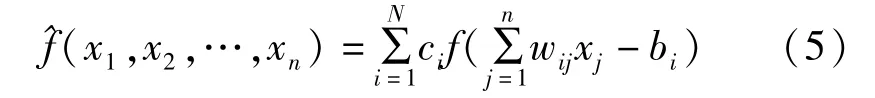
满足条件：

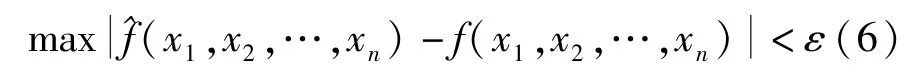
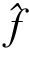
Kolmogorov 连续性定理从理论上保证了神经网络用于非线性时间序列的可行性，尤其是对高阶非线性函数的逼近。

4.2 强杂波背景下的PD 雷达导引头小目标检测

海杂波具有混沌特性，只需要对海杂波的时间样本序列求出其嵌入维和延迟时间，就可以对高维海杂波时间序列进行相空间的重构，从而实现对海杂波高维动力方程的非线性预测，我们令BP 网络输入的个数为嵌入维，采样时间与延迟时间保持一致，则BP 网络输入为：

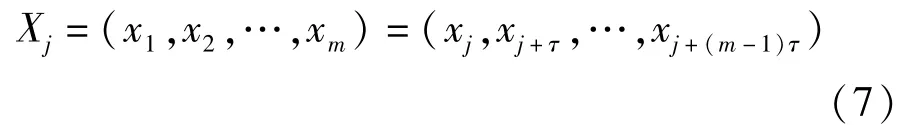
则BP 预测网络输出为：

式中：（·）——BP 网络的隐含层的激活函数，一般采用S 型；w——权值。

由此可得，海杂波背景下的目标检测器设计，如图4所示，隐含层的单元个数若取的太大，计算量大，隐含层的个数太少，逼近效果差，一般隐含层的个数取值为2＋1 时（为输入变量的个数），能够得到很好的逼近效果。

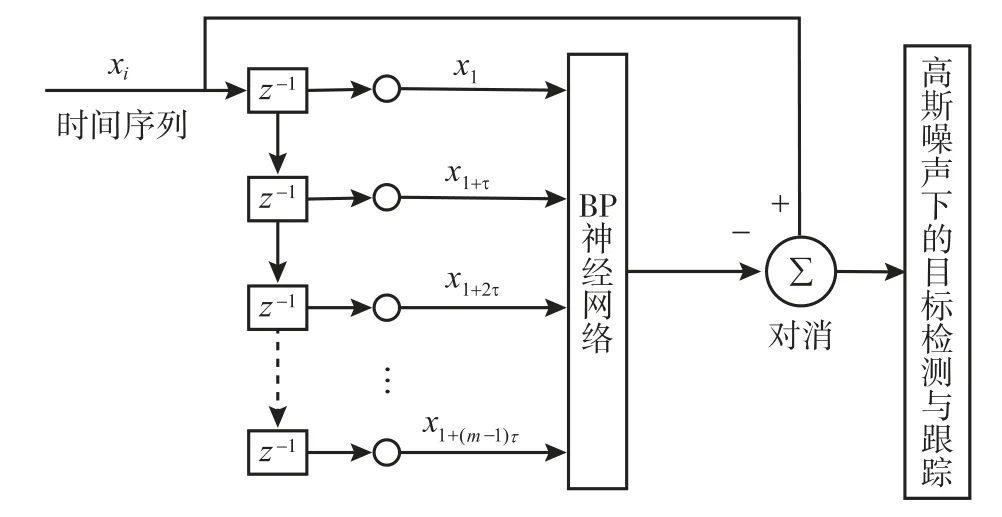
图4 基于BP 神经网络的非高斯背景下的目标检测框图Fig.4 The target detection in non-Gaussian background based on BP neural network

4.3 仿真与结果分析

在进行PD 雷达导引头的目标检测时，海杂波是叠加在导引头目标回波信号上的，可以认为海杂波与目标信号是相加的，以工作频率为35 GHz，目标多普勒频移为2 kHz 的PD 雷达导引头数据为例。

海杂波对消前后相参积累的检测结果如图5和图6所示，分别对对消前后的时间序列进行相参积累检测，然后对比海杂波对消前后的相参积累检测效果，图5的目标多普勒频偏为2 kHz，信杂比－22 dB，信号淹没在杂波下，对消后的信杂比改善3.68 dB；图6的目标多普勒频偏为2 kHz，信杂比1.3 dB，信号与杂波相当，对消后的信杂比改善2.62 dB。

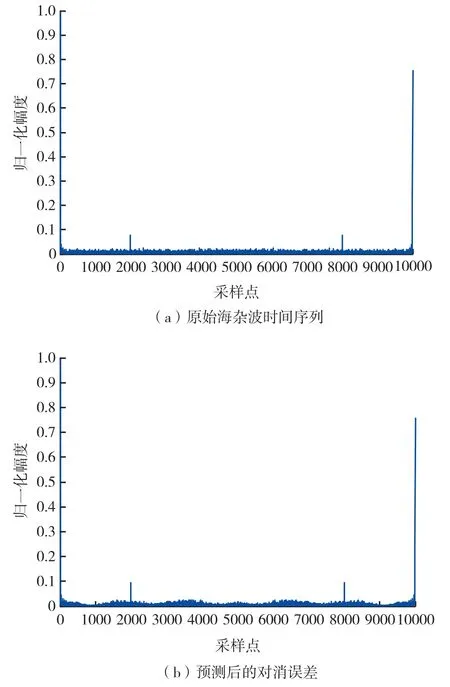
图5 信杂比－22dB 海杂波时间序列检测效果图Fig.5 The detection show of －22dB signal-to-clutter sea clutter time series

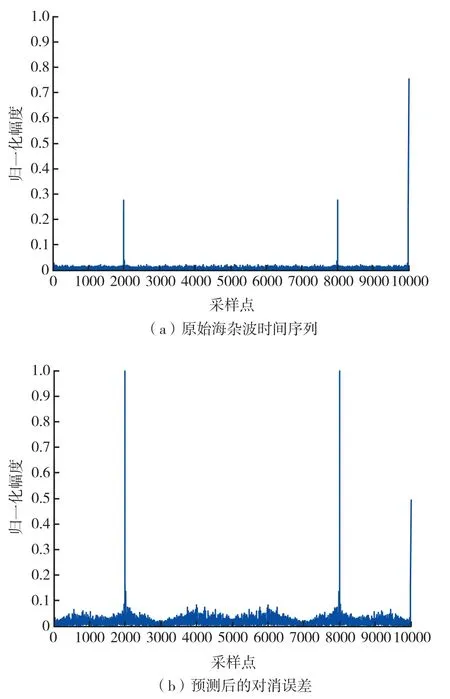
图6 信杂比1.3 dB 海杂波时间序列检测效果图Fig.6 The detection show of 1.3 dB signal-to-clutter sea clutter time series

运用蒙特卡洛仿真方法，进行强海杂波时间序列下的PD 雷达导引头的小目标检测，可以得到，对消后的信杂比改善一般在（2 ～6） dB，且对小信杂比信号的检测信杂比的改善相对明显，对大信杂比信号的检测无优势，这是因为在大信杂比条件下，信号能量比杂波信号强很多，在对消处理时，对信号的对消度大于对海杂波的对消度，因此，本检测方法适用于小信杂比强杂波背景条件下的PD 雷达导引头的小目标检测。

5 结束语

基于海杂波时间序列的混沌特性，采用BP 神经网络的强大非线性逼近功能，对海杂波时间序列进行预测与对消处理，进而实现强杂波背景下的PD雷达导引头的小目标检测，最后仿真试验证明了强海杂波对消处理后的目标检测性能的改善，提高了目标检测概率，提升了导引头威力。