一种互相关法测量相位噪声理论及仿真分析

沈晓宇张 亮曹 旭李宏宇刘宇轩袁 艳

（1.北京无线电计量测试研究所，北京 100039；2.航天系统部装备部装备保障队，北京 100094）

1 引 言

相位噪声是信号源、晶体振荡器、雷达等各种信号设备与系统的重要技术指标。 如今，随着众多新型技术的应用，各种低噪声信号源与高稳晶振不断问世，输出频率范围不断增大以及相位噪声不断减小，对相位噪声的测量提出了更高的要求。 传统的鉴相法测量相位噪声，为了避免参考源噪声底部的影响，通常要求参考源噪声底部优于待测源10 dB 以上，对于目标是超高指标的待测源而言参考源无法满足要求，从而就无法实现测量，互相关法是为了打破这一限制因素，在传统鉴相法基础上做出的改进。

基于MATLAB 的系统仿真模型进行互相关法测量相位噪声的研究，介绍了互相关法测量相位噪声的系统流程，并针对其抑制干扰噪声的原理，进行了理论分析与效果的仿真验证。 同时，分析了互相关法测量相位噪声过程中双通道相关性的影响，进行了仿真论证，仿真得到的结果与理论分析结果一致，该研究对于实际工程中相位噪声的测量，及相关仪器设备的研制具有一定的现实参考意义。

2 相位噪声理论基础

相位噪声有多种表征方式，应用最广泛的表征方式是单边带相位噪声谱密度，其定义为偏离载波频率处，单位赫兹的信号功率与载波功率之比为：

相位噪声与功率谱的对应关系如图1所示，相位噪声等于阴影面积除以载波功率。

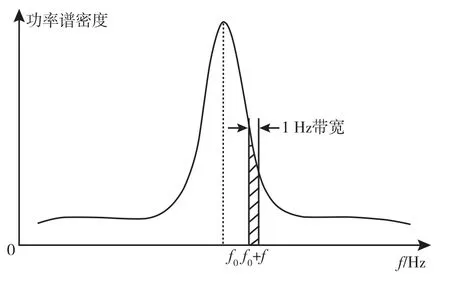
图1 相位噪声表征示意图Fig.1 Characterization of phase noise

3 互相关法测量相位噪声原理

互相关法测量相位噪声可以抑制不相关的噪声信号，从而实现超低相位噪声的测量，整体系统结构图如图2所示。

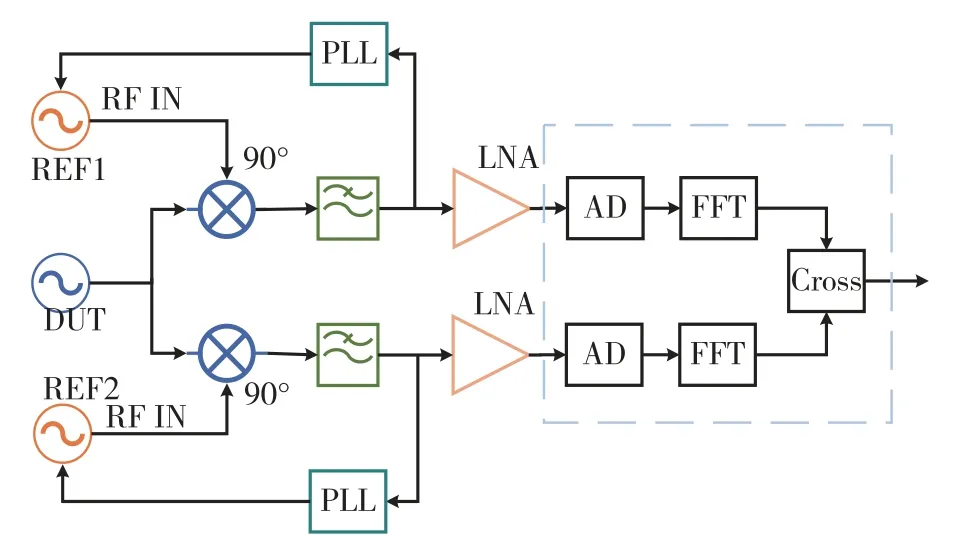
图2 互相关法测量相位噪声系统结构图Fig.2 System structure of noise measurement system by cross-correlation method

系统包含一个待测源与两个参考源，设置参考源信号与待测源信号同频正交，待测源信号通过功分器分为两路信号，每一路待测信号与参考信号经过鉴相器混频，再通过低通滤波器滤除高频分量得到待测相位噪声。 根据所选AD 芯片的满量程输入功率，用低噪声放大器将输入AD 芯片的噪声信号放大到适合的功率范围，利用AD 芯片完成模拟信号到数字信号的转换，于FPGA 中进行FFT 运算并将运算结果发送到上位机，上位机进一步完成互相关计算，得到最终的待测噪声信号的功率谱，并绘制相位噪声曲线。

互相关算法实现集中在数字处理模块，即图中虚线框内部分，目标是将AD 芯片采集到的噪声信号转换为功率谱估计值，目前关于功率谱估计方法有两种定义，分别称为直接估计法和间接估计法。

3.1 间接估计法

依据维纳－辛钦定理，求被观测信号样本序列［］的自相关函数r（），再对其做傅里叶变换，将傅里叶变换结果作为功率谱估计值。

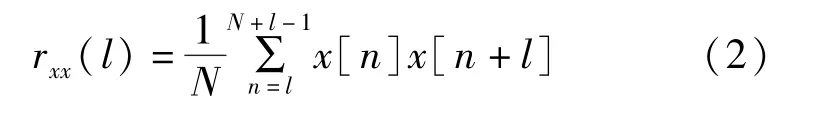
式中：——相关运算的点数；—延迟间隔。

则功率谱估计值S（）为：

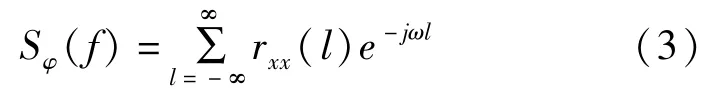
3.2 直接估计法

直接法是Schuster 在19 世纪末提出的方法，它的计算方法是先对信号序列［］求其傅里叶变换，变换结果乘自身的共轭并除以序列长度，所得结果作为功率谱估计值。

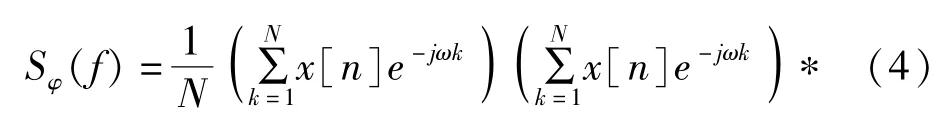
当的值较小时，两者计算量差别不大，当增大时，间接估计法中求相关函数的计算量陡增，在工程应用中不再实用。 比较而言，直接估计法不需要计算信号序列［］的自相关函数，只需要对输入序列求傅里叶变换，再加简单计算即可得到功率谱估计值，益于FFT 的应用，傅里叶变换可以快速计算得出，所以S（）可以比较快速地算出，因此，工程上我们使用直接估计法进行功率谱估计。

基于直接法求两个不同信号序列［］和［］的互相关功率谱估计值S（），则为两个序列FFT变换后共轭相乘并除以序列长度。

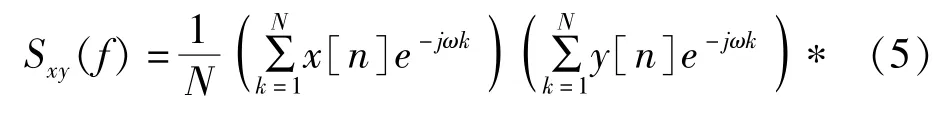
计算结果为复数，工程和实验中取S（）的模值作为互相关功率谱估计值，简称互功率谱估计值。

3.3 互相关算法原理

采用直接估计法进行功率谱估计，分析这一过程中实际的双通道信号互功率谱估计值的计算，假设（），（）为双通道信号，对应傅立叶变换为，变换关系如式（6）所示：

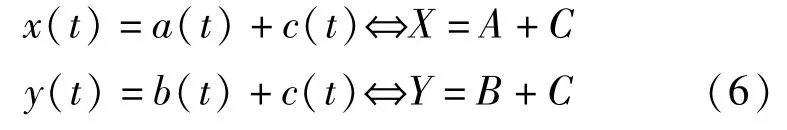
式中：（）——干扰高斯白噪声信号1；（）——干扰高斯白噪声信号2；（）——待测高斯白噪声信号；——（）的FFT 变换；——（）的FFT 变换；——（）的FFT 变换。

分析过程中，选择以高斯白噪声为研究对象。

美国国家标准协会（American National Standards Institute）提出定义，频率源的相位噪声主要由5 个相互独立的随机过程组成，并建立了相位噪声的幂律谱模型，如式（7）所示：

式中：S（）——被测频率信号的相对频率波动谱密度；——各噪声分量的系数；f——噪声的有效带宽；——各噪声分量的编号。

根据幂律谱模型，美国学者Enrico Rubiola F 和Fran＿cois Vernotte 指出并证明，各种有色噪声均可通过与适当的幂相乘转换为白噪声，再通过除幂恢复得到原有色噪声而不影响其功率谱密度特性，基于这一性质，针对有色噪声的研究通常都是将其转换为白噪声进行分析，再通过恢复转换得到相应的结果。 因此，在互相关计算的推演过程中只需以白噪声为研究对象即可。

定义运算符号（）＝（＋＋……＋a），其中为可替换的任意变量，设S为（），（）信号的互功率谱估计值，实际工程中要求得的（），（）信号次互相关所对应的功率谱估计值，即为S求次平均后的模值，结果如式（8）所示：

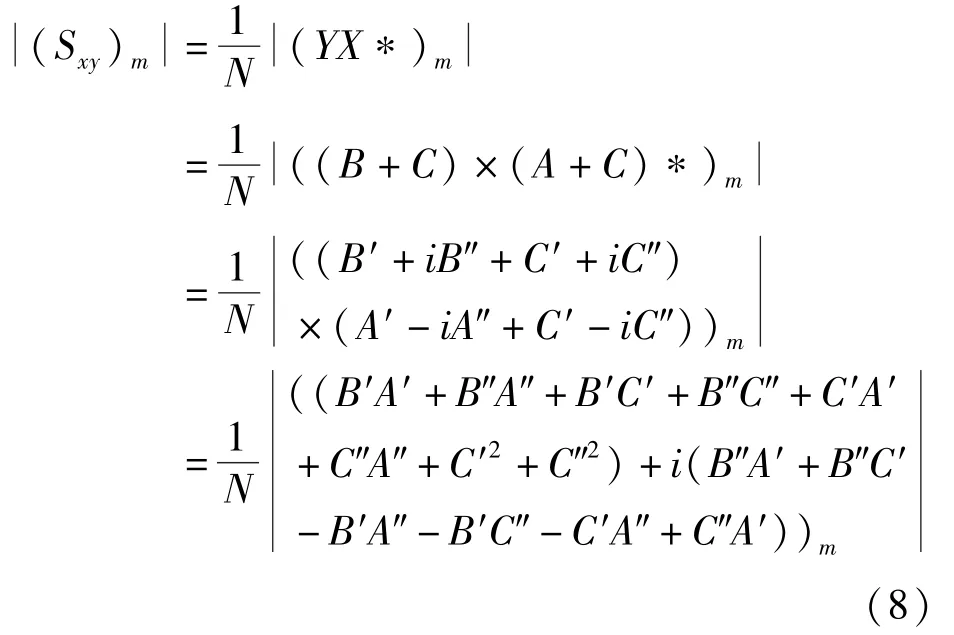
式中：——FFT 运算点数；，，——对应矢量的实部；，，——对应矢量的虚部。

表1 分量特征Tab.1 Feature of component

记为：

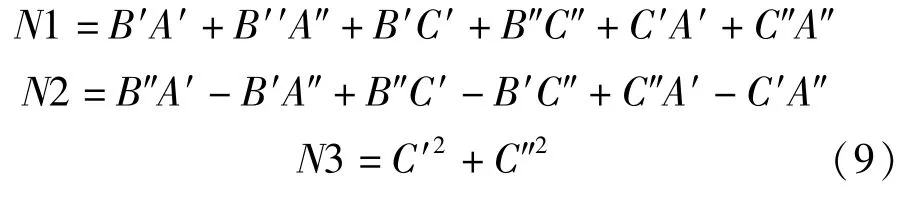
代入式（8），可得：

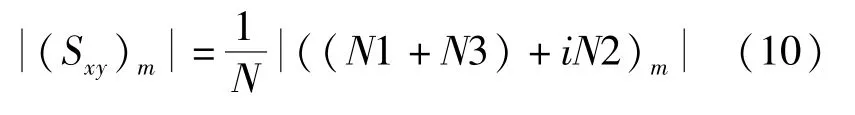
结合表1与式（9），进一步得到1，2，3 特征如表2所示。

表2 化简后的分量特征Tab.2 Features of simplified component

由式（10）发现，目标估计量3 存在于（S）的实部，所以对于互相关法测量相位噪声而言，优化的功率谱估计方案是不取（S）的模值，而是取（S）的实部绝对值作为最终估计结果，从而消除虚部干扰项带来的误差，此时误差项仅为1。 当≥10时，测量结果近似等于1 绝对值与3 绝对值之和，即：

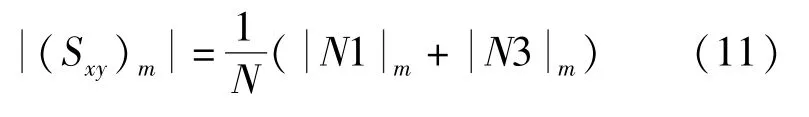
令＝1＋212（1＋2），则不相关项1 绝对值的数学期望计算如式（12）所示：

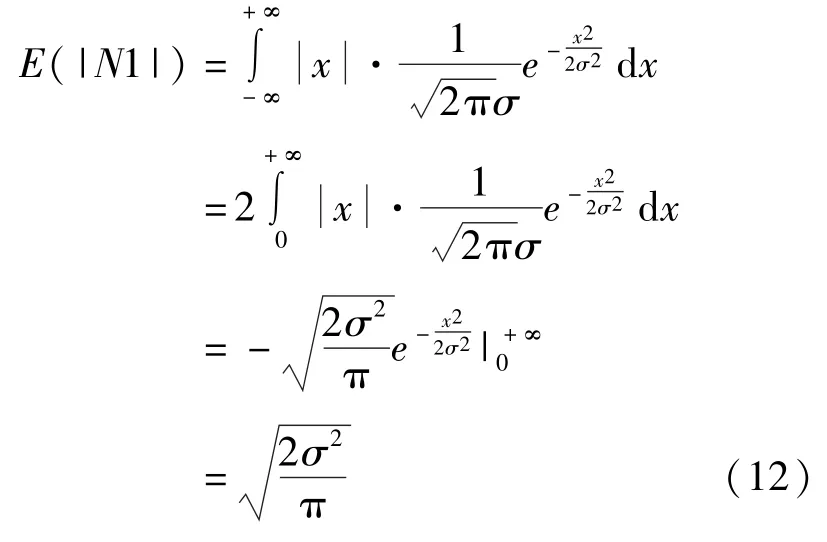
次互相关后的计算结果为：

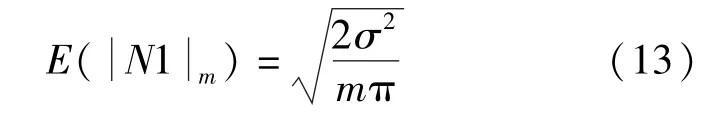
由此可以得出结论，采用取实部绝对值的方法，不相关噪声功率谱密度满足互相关次数增大倍，均值减小的规律，相比取互功率谱模值，取实部绝对值的方法更具优势，体现在同条件下估计结果更加准确，计算量更小，运算速度更快。

4 互相关法测量相位噪声仿真

互相关法测量相位噪声仿真流程如图3所示。

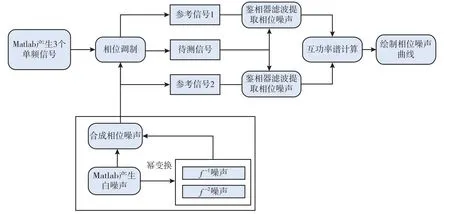
图3 互相关法测量相位噪声仿真流程图Fig.3 Simulation process of measuring phase noise by cross-correlation method

第一步，使用MATLAB 自带函数产生高斯白噪声序列，再根据幂率谱模型通过幂变换产生，两种有色噪声，将三种噪声线性叠加来模拟相位噪声，通过调整三种噪声的幅度系数，使产生的相位噪声满足表3中的设置（误差0.5 dBc／Hz）。

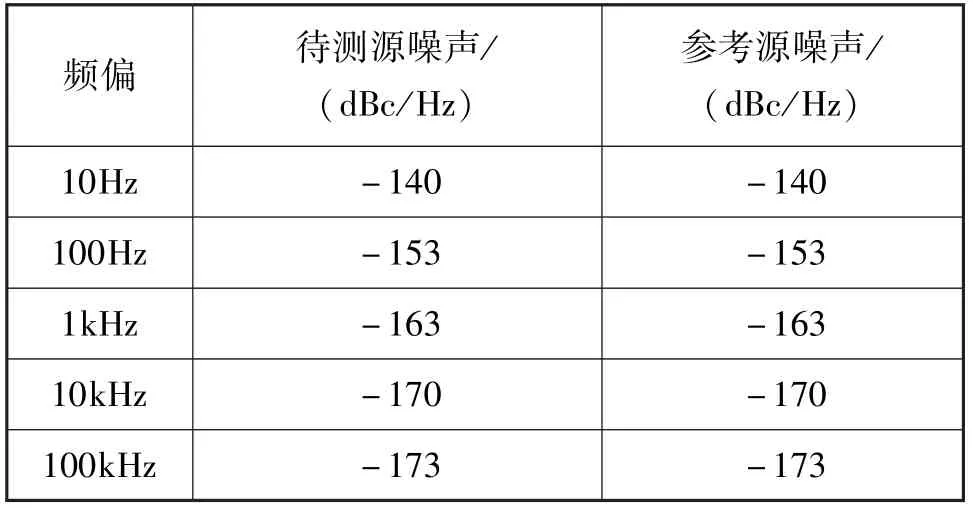
表3 相位噪声设置Tab.3 Setting of phase noise

第二步，使用MATLAB 产生3 个纯净的单频信号，为方便计算，功率均设为0dBm，将产生的相位噪声与单频信号叠加，得到含相位噪声的待测信号与参考信号。

最后，通过鉴相法提取相位噪声并进行互功率谱计算，绘制相位噪声曲线。

4.1 效果验证

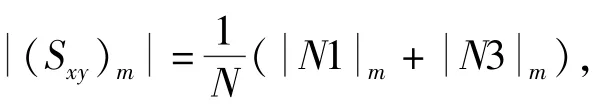
进行单通道鉴相法测量，仿真得到的相位噪声曲线结果如图4所示。

图4 单通道测量的相位噪声曲线图Fig.4 Curve of phase noise in single channel

仿真得到的数据统计结果如表4所示，由于仿真得到的实测噪声为待测源噪声与系统噪声的叠加，在既定参数下，相位噪声数值上将比实际待测源噪声高3 dBc／Hz，此时相位噪声测量受系统噪声限制作用较为明显。

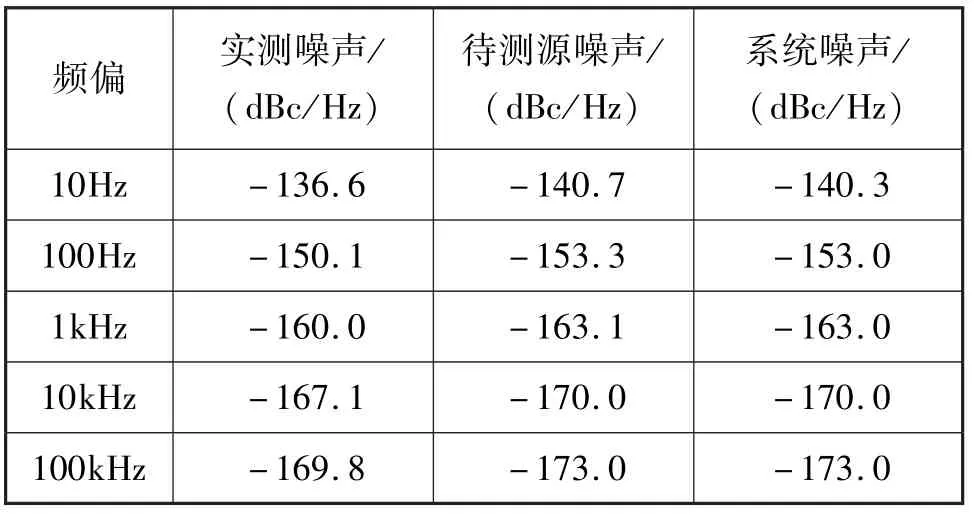
表4 单通道测量相位噪声统计结果Tab.4 Statistical results of phase noise in single channel

进行10 次互相关运算，仿真得到的相位噪声曲线结果如图5所示。

图5 10 次互相关后相位噪声曲线图Fig.5 Curve of phase noise after 10 times of cross-correlation

仿真得到的数据统计结果如表5所示，相比单通道鉴相测量，系统噪声降低约5 dBc／Hz，与推论结果一致，得到的相位噪声波动减小。

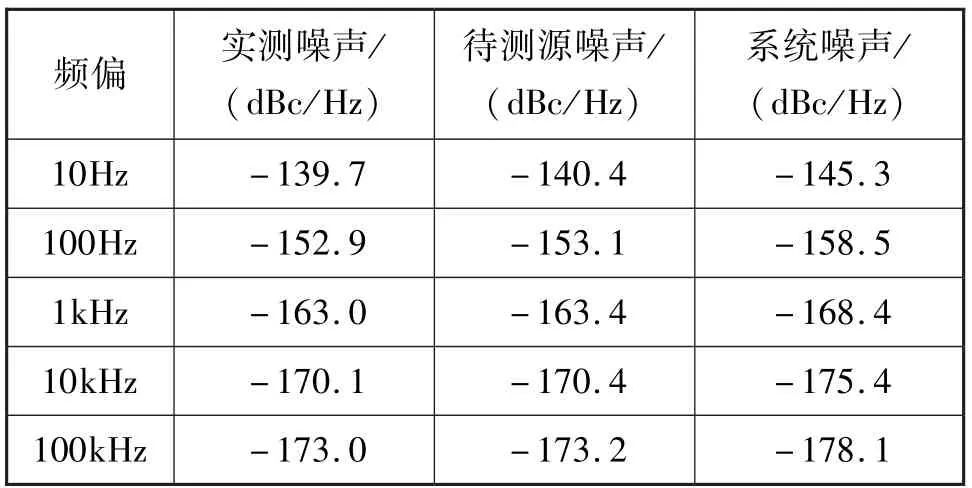
表5 10 次互相关后相位噪声统计结果Tab.5 Statistical results of phase noise after 10 times of cross-correlation

进行100 次互相关运算，仿真得到的相位噪声曲线结果如图6所示。

图6 100 次互相关后相位噪声曲线图Fig.6 Curve of phase noise after 100 times of cross-correlation

仿真得到的数据统计结果如表6所示，可以看出，进行100 次互相关后，系统噪声降低约10 dBc／Hz，与推论结果一致，得到的相位噪声曲线波动进一步减小，与实际待测源噪声误差小于0.5 dBc／Hz。

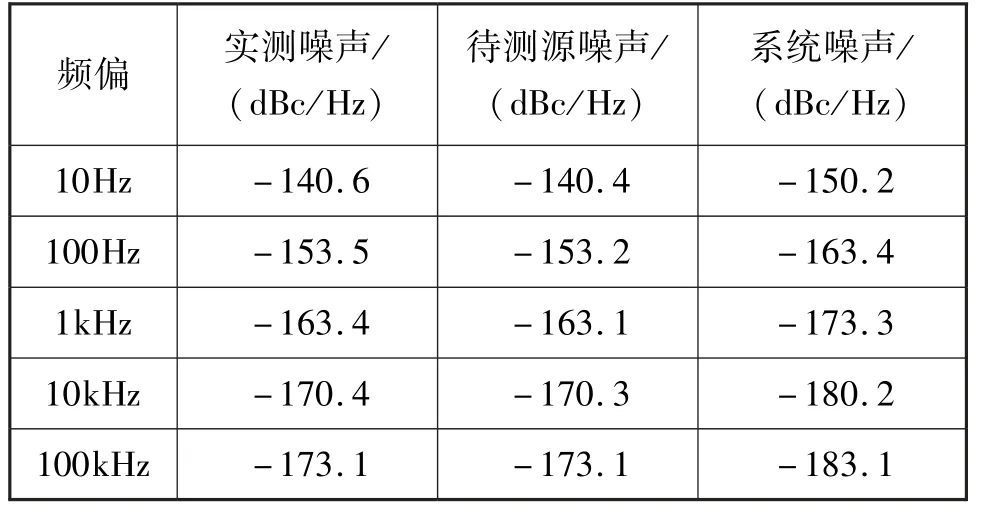
表6 100 次互相关后相位噪声统计结果Tab.6 Statistical results of phase noise after 100 times of cross-correlation

综上，互相关次数增加倍，系统噪声将随之降低5lg（m）。 但是在工程环境下，互相关次数成倍增加的同时，系统计算时间也会成倍增加，所以在确定互相关次数上限时，需综合考虑硬件水平与算法速度。

4.2 双通道信号相关性的影响

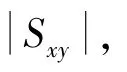
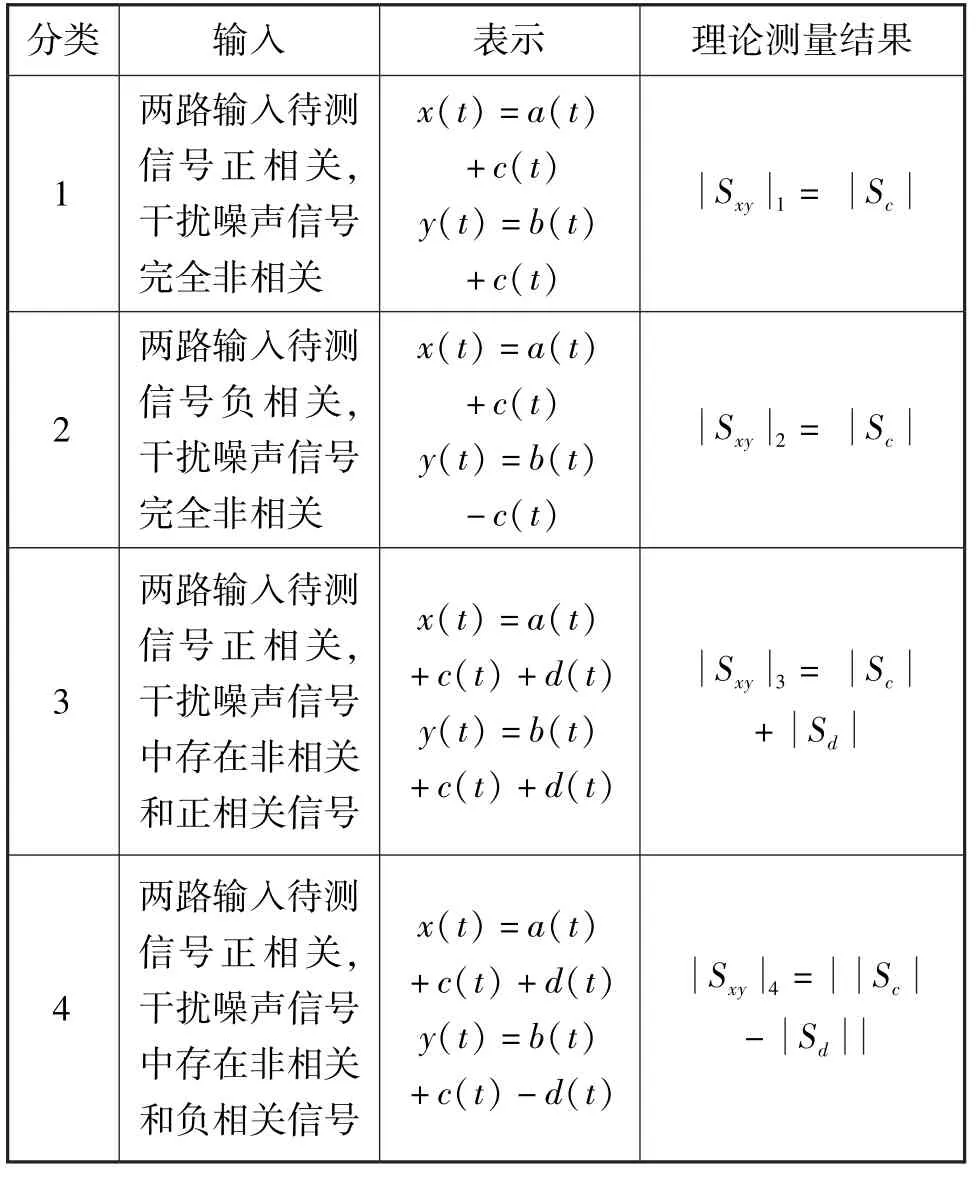
表7 双通道信号相关性分析Tab.7 Correlation analysis of dual channel signals

结论：双通道中待测信号的正负相关性对结果无影响，而干扰信号中的正负相关信号将直接叠加到待测信号上，且无法通过互相关运算抵消。

下面针对四类情况进行结论的证明，第1、2 类情况的证明相对简单，只需要将式（6）中的（）变为－（），推导过程不变，即可证明推论的正确性，这里不再重复，现在对第3 类情形作展开分析，分析如下：

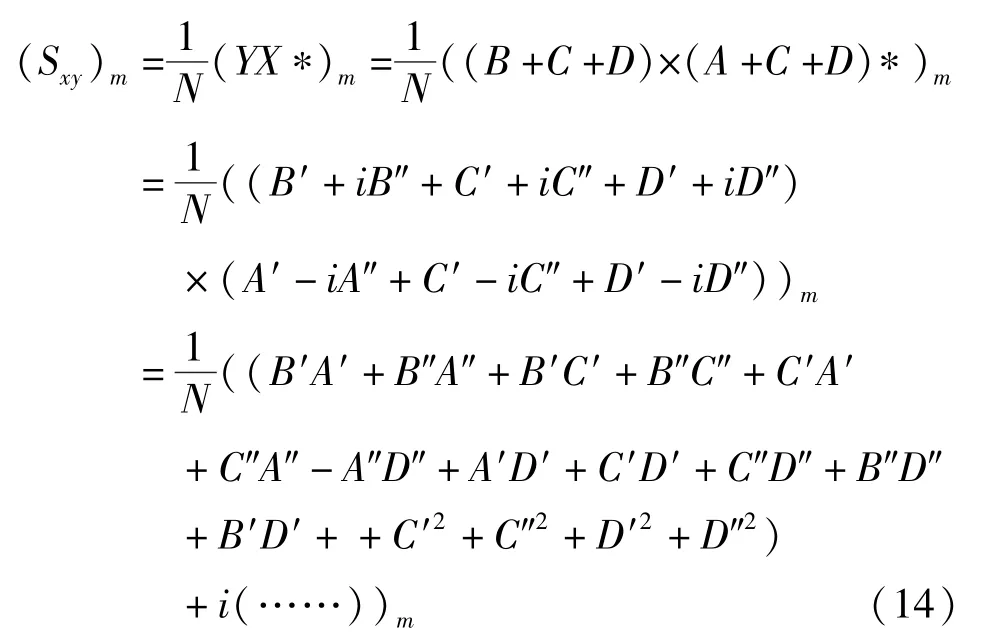
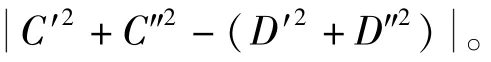
通过仿真实验验证相关性的影响，具体方案是产生一段噪声分别叠加到双通道信号上，则叠加的噪声具有相关性，为突出对比效果，调整该噪声功率大小为待测源噪声的0.8 倍，通过正负叠加来控制干扰噪声的正负相关性。 设置互相关次数为10并进行10 次仿真实验，记录特定频点的相位噪声大小，取10 次所得数据的平均值作为最终数据并进行比较。

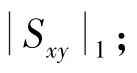
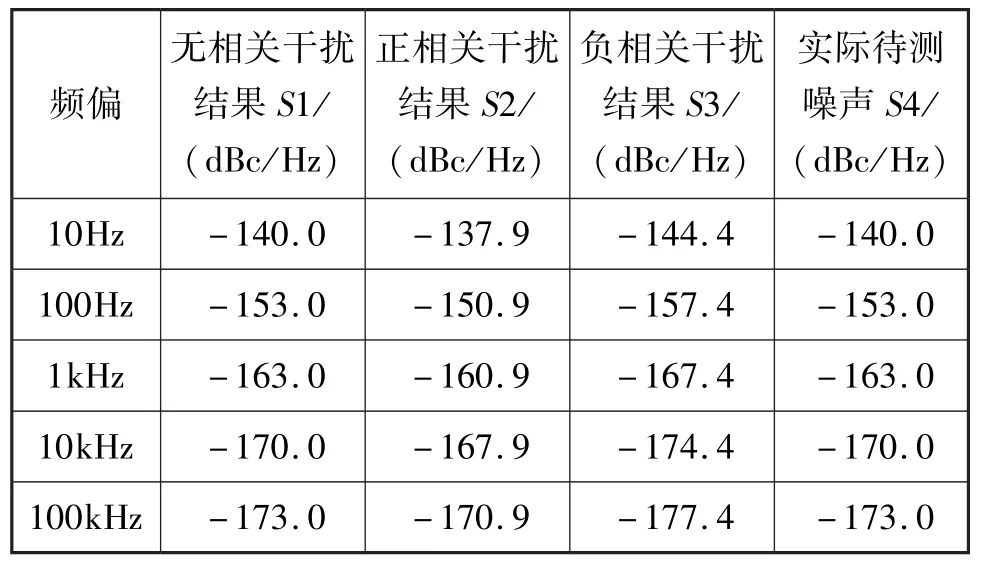
表8 相关性相位噪声数据理论结果Tab.8 Theoretical results of correlated phase noise data

仿真得到的相位噪声曲线结果如图7所示。

图7 相关性相位噪声曲线仿真结果图Fig.7 Simulation results about correlation of phase noise

仿真得到的数据统计结果如表9所示，与表8理论结果相符，数值误差小于0.5 dBc／Hz。

表9 相关性相位噪声数据统计结果Tab.9 Statistical results of correlated phase noise data

综上，双通道中的相关干扰信号会显著影响测量结果，该影响无法通过增加互相关次数进行抵消，保持双通道不相关对于得到准确的计算结果具有重要意义，是发挥互相关作用的关键。

5 结束语

针对互相关法测量相位噪声进行了理论分析与仿真验证，证明了随着互相关次数的不断增加，系统噪声底部不断降低，不相关噪声产生的影响被有效抑制，从而满足超低相位噪声的测量需求。 同时对互相关计算过程中双通道相关性影响因素进行了理论分析与仿真验证，所得到的推论及仿真结果对相位噪声测量系统的研制，及相关的理论研究具有重要的参考价值。