Risk modeling of femoral neck fracture based on geometric parameters of the proximal epiphysis
2022-08-19AnnaShitovaOlgaKovalevaAnnaOlsufievaInchekhanumGadzhimuradovaDmitryZubkovMikhailKniazevTatyanaZharikovaYuryZharikov
lNTRODUCTlON
Fractures of the proximal epiphysis of the femur are problematic for state health care because they are associated with severe medical and social problems[1], high morbidity rates[2], disability[3,4], and high mortality rates[5]. Bone strength depends on the mineral density, architectonics and remodeling ability of bones[6], which change over time due to various factors. Characteristics such as bone mineral density, bone geometry and the properties of bone materials are factors that constitute bone quality[6]. The process by which bone strength decreases due to chemical composition changes and by which it decreases in trabecular density is referred to as osteoporosis[7].
The results of multiple studies on the causes and risk factors of bone deterioration, such as osteoporosis, have been introduced in clinical practice. The Fracture Risk Assessment Tool (FRAX)[8] scale was developed by individuals at the University of Sheffield to evaluate fracture risk; the scale assesses the influence of factors that cause a decrease in bone strength. The FRAX scale allows us to predict the ten-year probability of fracture, to identify patients who require more detailed examinations, including X-ray densitometry, and to prevent excessive radiation exposure[9].
In recent years, numerous studies have investigated the distribution of strain in bone under an applied load, identified areas that are highly influenced by stress and fracture risk and determined the influence of bone cytoarchitectonics and geometry on stress apportionment. High-resolution computed tomography and magnetic resonance tomography are employed in this field to analyze bone morphometric parameters[10]. Finite element analysis is a technique that is widely employed for bone model construction[11]. MATLAB is frequently utilized to calculate stress distributions in bone models[1]. The authors assessed changes in bone sample flexibilitya microhardness tester[12]. Other authors have detected structures in loaded femursa tension detector fixed to the bone[13]. The results of these investigations have been implemented in osteosynthesis operations[14] and endoprosthesis engineering applications[15].
This study aimed to determine the geometric parameters of the proximal femur that contribute most to femoral neck fracture. A method for measuring bone geometric parametersX-ray images is provided since X-ray images are widely employed by general practitioners, and thus, may be preferable for use in screening studies. According to this finding, in this study, we will mostly rely on X-ray imaging, as a widely utilized diagnostic method.
MATERlALS AND METHODS
Seventy femurs from the records of the Department of Human Anatomy at Sechenov University from people aged 14 to 80 years were selected to measure geometric parameters of the proximal epiphysis.
At other times both leaves were held in the backward eddy, and failed to reach the main current of the noisy stream What are you doing? asked the king at last, and the hermit replied that he was reading the fates of men; every one s fate, he said, was settled from the beginning, and, whatever it were, there was no escape from it
The projection values of the proximal epiphysis of the femurs from the Department of Human Anatomy and geometric parameters of the bones shown in the X-ray images were measured with Autodesk software (AutoCAD 2018).
Method of measuring bone geometry parameters
To ensure accurate measurements, centimeter rulers were attached to the bones, which helped to correctly scale the images. The projection that defines the femoral neck base and accuracy of the neckshaft angle (NSA) measurements,, the frontal standard projection (FSP), was selected to plot the segments signifying the main geometric parameters of the proximal epiphysis of the femur.
The angle of bone rotation obtained by turning the cube corresponded to the angle measured with the second technique, which uses the previously described feature of the large spit. Thus, this method of calculating the rotation of the bone relative to the anterior projection was deemed reliable and utilized in subsequent calculations. During the rotation of the bone around axis AB to a random angle, triangle ABC was projected onto ABC1.
The triangle ABC designations, which are employed in formulas, comprising NSA (angle CAB); AC, the neck axis; and AB, the diaphyseal axis segment (connecting the diameter of the diaphysis to the neck axis), were plotted (Figure 1A) as a major component of the epiphysis of the proximal femur.
The angle between the principal compressive trabecular pattern and the secondary compressive group [angle of the minimal resistance zone (AMRZ)] was applied to assess the value of Ward’s triangle. The principal compressive trabecular pattern and secondary compressive group are indicated by segments KL and LJ, respectively. Segment KL was defined as the segment from the upper projection point of the distal base of the neck (point K) to the lower projection point of the lesser trochanter (point L). The segment LJ was defined as the segment parallel to the mechanical axis, which connects the center of the femoral head to the point between the femoral condyles and passes through point L (Figure 1B).
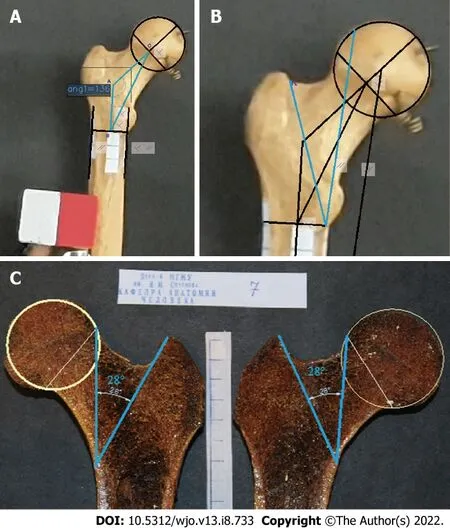
The minimal resistance zone was demonstrated using photos of gross sections of the proximal epiphysis of the femur from the Department of Human Anatomy at Sechenov University. Trabecular patterns, following the course of the main forces acting on the femoral epiphysis under physiological vertical loading, were clearly visualized on the gross sections. The direction of the chosen segments corresponded to the physiological stress lines and comprised a zone containing fewer trabeculae than were present in adjacent areas (Figure 1C).
The projection values of the proximal femoral geometry parameters are equal to their actual values if the bone is positioned such that the planes of the CAB and KLJ triangles are parallel to the plane of the screen onto which the bone is projected. If the bone is somehow rotated, its parameter cannot be measured directly. Therefore, the bone elements that can assist in determining the presence of bone rotation relative to the standard projection and in measuring its angle were selected.
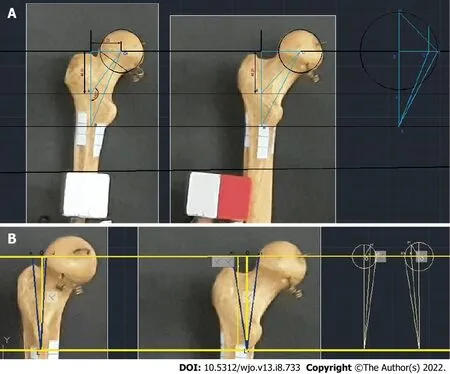
When analyzing the video frames that show bone rotation, we determined that the greater trochanter can be inscribed in a parallelepiped, one of the faces of which is a rectangle when the bone is in FSP. Consequently, this geometric parameter was chosen to evaluate the rotation of triangle ABC relative to the anatomical axis, to which segment AB is parallel. Thus, on an X-ray, the angle of rotation of the bone relative to the FSP can be determined by calculating the angle of rotation of the parallelepiped that contains the greater trochanter using spatial construction (Figure 2).

To assess the reliability of determining the angle of rotation on the basis of the greater trochanter, this angle was calculated by measuring the angle of rotation of the cube fixed to a tripod using the following formula:
QCN =135°- arcos (a1/a), where a is the edge of the cube (whose length is 50 mm) and a1 is the length of the cube verge in a projection other than the FSP.
In this study, a method for assessing the morphometric parameters of the proximal femur based on the projection values and angle of rotation around the anatomical axis relative to the FSP was developed. In this study, the rotation angle was determined by the rotation of the cube installed on the tripod turning the bone. The rotation of the cube thus indicated the rotation of the bone at every point in time. The anatomical axis was drawn through the midpoint of the diaphyseal diameter. The mechanical axis passed through the center of the femoral head and the midpoint of the distal epiphysis of the thigh bone (half of the distance between the condyles). The femoral neck axis was determined by the segment passing through the center of the femoral head and the plane perpendicular to the midpoint of the upper base of the femoral neck.
A video of femur rotation around the anatomic axis (for the estimation of the bone projection changes during the turning process) and stills from the video and X-ray images of the femur of 10 adult patients (18-24 years) were provided by the Department of Human Anatomy at Sechenov University (18-24 years), and 10 images of adult patients (18-63 years) were provided by the Department of Traumatology, Orthopedics and Disaster Surgery of Sechenov University (18-63 years). These X-ray images contained images of both femurs: one femur was fractured, and the other femur was intact and considered equal. The parameters of the fractured bone were measured using images captured with a Canon d60 camera.
The change in the projection value of the NSA as a function of the angle of the rotation is represented by the following equation:
CAB = 180°-arctg (SA/(SC1/cosHSC)), where HSC is the angle of rotation, SA is the segment of the diaphyseal axis, and SC1 is the perpendicular segment, which passes through the center of the head of the femur to the diaphyseal axis (Figure 3A).
The wolf ran as fast as he could, taking the shortest path, and the little girl took a roundabout way, entertaining herself by gathering2 nuts, running after butterflies, and gathering bouquets3 of little flowers. It was not long before the wolf arrived at the old woman s house. He knocked at the door: tap, tap.
Based on the abovementioned findings, the formula for calculating the true value of the AMRZ takes into account the rotation of the bone:
KLJ= acrtg (KO/(cos (KOH) × OL)) + arctg (OJ/(cos (JOH) × OL)), where KLJ is the projection AMRZ, KLJ 1 is the true AMRZ, KO and OJ are segments of the perpendicular line toward the diaphyseal axis passing through point J (Figure 3A), and KOH and JO indicate the angle of rotation.
Determination of the true parameters of the proximal epiphysis of the femur from an X-ray
A technique is proposed for determining the angle of rotation of the bone relative to the plane of the Xray image based on the estimated rotation of the greater trochanter. In this technique, a box is created around the greater trochanter. Geometric constructions (Figure 2) are performed to estimate the angle of rotation similar to the technique previously mentioned for native bones and their videos.
Subsequently, this value is used to determine the true AMRZ. The change in the projection magnitude of the NSA as a function of the angle of rotation can be represented by the following equation:
The true value of the AMRZ was calculated as follows:
CAB = 180o-arctg (SA/(SC1/cosHSC)), where HSC is the angle of rotation, SA is the segment of the axis of the diaphysis, and SC1 is the segment of the perpendicular line connecting the center of the femoral head to the axis of the diaphysis (Figure 3B).
KLJ= acrctg (KO/(cos (KOH) × OL)) + arctg (OJ/(cos (JOH) × OL)), where KLJ is the AMRZ projection, KLJis the true AMRZ, KO and OJ are segments of the perpendicular line toward the axis of the diaphysis drawn through point J (Figure 2), and KOH and JOH are the angles of rotation (Figure 3B). When the plane including the axes of the neck and diaphysis is parallel to the plane of the X-ray, it is possible to directly measure the AMRZ (Figure 4).
How I wish a colorful bundle of fresh wildflowers could reflect the beauty of your way with children-the constant patience and nurturing6, the gentle encouragement. A keepsake basket laden7 with soothing8 soaps and bath oils would eventually serve only as a common gift were its sturdy, woven walls not filled to overflowing9 with examples of the individual ways you have touched the lives of your students.

This study does not take into account any parameters other than geometric parameters. Sex, age, concomitant diseases and other conditions can affect these parameters, but this study evaluates the results of these effects.
RESULTS
Interrelations among proximal femoral morphometric parameters
The results of a statistical analysis of the geometric parameters of the proximal epiphysis of the femur are presented in Table 1.

The correlation coefficient for the correlation between the NSA and the AMRZ, for the correlation between segment BC and the zone of minimum resistance, and for the correlation between the length of segment BC and the upper-to-lower neck length ratio was -0.155, 0.0617, and -0.119, respectively, which indicates weak negative correlations among these parameters. These findings suggest that the NSA and AMRZ vary independently of each other, and regarding the influence of these changes on the risk of fracture of the femoral neck, they must be evaluated as independent values. The correlation coefficient between the NSA and the upper-to-lower neck length ratio was -0.396, that is, there was a moderate negative correlation between these parameters.
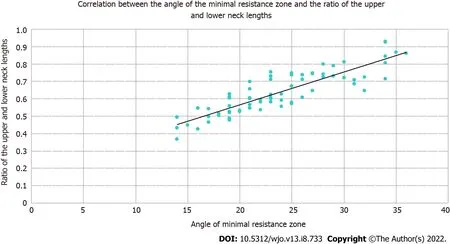
The strongest correlation was found between the AMRZ and the upper-to-lower neck length ratio, with a correlation coefficient of 0.872 (Figure 5). Based on this finding, we use the upper-to-lower neck length ratio to determine the size of the AMRZ.
Model of the proximal epiphysis that provides a minimal risk of femoral neck base fracture
The scale needs to be evaluated further in future studies and is not ready for use in clinical practice. However, the measurement of these parameters during screening studies can reduce the risk of severe injuries.
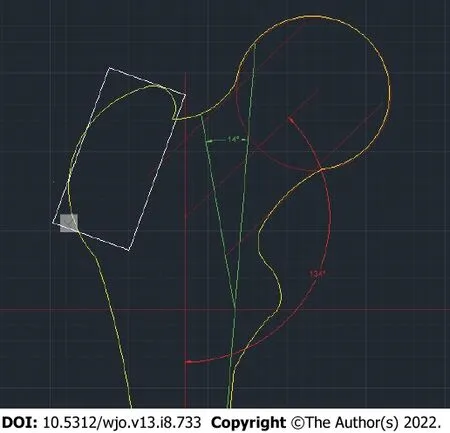
The femoral proximal epiphysis, which has parameters included in this model, is the most resistant to femoral neck base fracture when a patient falls on his or her side, according to our study.
Evaluation of the risk of femoral neck fracture using X-ray images
The scale was developed to evaluate the risk of femoral neck base fracture (Table 2). Scores were assigned to bone parameters within certain intervals, as specified in the table. According to the sum of the points, the degree of fracture risk for a given bone was determined: 2 points indicated low risk, 3-4 points indicated average risk, and 5-6 points indicated high risk. The analysis of 10 X-ray images stored in the Department of Human Anatomy and 10 X-ray images of patients from the Department of Traumatology, Orthopedics and Disaster Surgery of Sechenov University showed that the value of the NSA and AMRZ differed from the optimal value for all bones.

DlSCUSSlON
We aimed to determine the bone parameters that are risk factors for a fracture of the base of the femoral neck when the patient falls on his or her side and did not take into account other types and mechanisms of fracture. However, the selected optimal values still remain within the reference values, even if they increase the risk of other mechanisms of femoral fracture.
In our study, we agree with the finding of several authors[16-20] that some bone parameters, such as NSA, have optimal values, and their deviations can cause a higher risk of fracture. In another study, the NSA value had a weak correlation with the size of the minimum resistance zone of the proximal femur (AMRZ), indicating that these parameters can independently influence fracture risk.
Their old father gave each of them a fine horse; the one who knew the dictionary and the daily paper by heart had a black horse, while the other who was so clever at corporation law had a milk- white one
According to previous studies, neither a decrease in the NSA nor an increase in the NSA can be considered a reliable risk factor for femoral neck fracture since there are data that both confirm and disprove the influence of these factors on the probability of fracture[21-23]. Nevertheless, it has been confirmed that the strength of the proximal epiphysis decreases when the NSA decreases, and the stress that occurs in the proximal epiphysis under stress conditions shifts to its distal part. The femoral neck can be considered a lever, to the ends of which forces are applied. In this case, the value of the moment of forces that characterize the rotational action of forces acting on the proximal and distal part of the neck relative to the middle of the lever will increase as the NSA decreases. Based on measurements and a fracture risk assessment in another study, we assume that reducing the NSA causes an increase in the risk of femoral neck base fracture.
In the field of orthopedics, proximal femur modeling is utilized to plan interventions and assess their results[24]. When planning corrective osteotomy, to calculate the true value of the NSA using X-ray images, the researchers employed X-ray images of the hip joints projected directly in the middle position, with internal rotation of the thigh, and in a position proposed by Lauenstein, with the mathematical tables proposed by Strzyzewski or Shartlain[19]. However, these measurements allow only approximate planning of the surgical intervention, so the results of the treatment depend heavily on the personal skills of the surgeon. 3-D modeling is considered a more accurate method; therefore, algorithms for calculating surgical interventions on 3D models have been introduced and are highly distributed[24-27].
Furthermore, modeling of the proximal femoral epiphysis is conducted to create mathematical models to assess the risk of fractures under the influence of external factors. In recent years, special attention has been given to the variability of the shape of the proximal femur and the influence of its geometry on its strength[28]. For this purpose, statistical shape models are employed to simultaneously assess the impact of risk factors and pathological changes in a variety of bone geometric phenotypes[29]. The analysis of the geometric and strength characteristics of cadaveric proximal femurs continues to be applied for more accurate construction of mathematical models[30,31].
However, in most cases, statistical shape models require three-dimensional images using tomographic methods. Since the 3D model is associated with a high computational burden, Jazinizadeh[32] compared the ability of 2D and 3D femur models to predict hip fracture risk and showed that their productiveness does not differ significantly.
We propose a method for calculating the true parameters of the proximal epiphysis based on one projection obtained using an X-ray image. Our technique is assumed to prevent the occurrence of femoral fracture in primary health care practice, unlike other techniques designed to correct the consequences of a fracture. We assume that our method can be used in combination with existing methods for assessing the risk of fractures, since it does not contradict but can complement other methods.
Our study has a retrospective design, which is its first limitation. In the course of this work, a small number of X-ray images were selected; other types and mechanisms of fracture were not taken into account; and any parameters of bone tissue, other than geometric characteristics, were not taken into account. With regard to the selection of cadaveric bones, the age, gender and other parameters of the owners of the bones were not taken into account. In addition, the impact of other risk factors for hip fractures has not been evaluated, and densitometry studies have not been performed.
But instead of sleeping he only lay awake and thought of the hermit s prophecy; and the more he thought of it the angrier he felt, until he gnashed his teeth and declared that it should never, never come true
The model of the proximal epiphysis, which provides a minimal risk of femoral neck base fracture, consists of an NSA of 134° (which is 1° smaller than the mean of the maximal and mean values of this parameter shown in our study (144°+125.9°)/2 = 134.99)) and an AMRZ of 14° (minimal value of the parameter in our study) (Figure 6).
The suggested method for measuring the true parameters of the proximal femur does not require special equipment but is quite difficult to implement. This method can be used when special software is not available and in combination with other screening tools that use X-ray scans of the femur. Further improvements to this method are needed. Nevertheless, performing such measurements with modern X-ray diagnostic systems is not difficult. This method is assumed to be combined with other screening techniques and to be employed when other less complicated measurement methods are not available.
Ali Baba, who expected a dull, dismal5 place, was greatly surprised to find it large and well lighted, hollowed by the hand of man in the form of a vault6, which received the light from an opening in the ceiling
CONCLUSlON
Disease prophylaxisthe assessment of risk factors and prevention is essential in modern medicine. Therefore, methods for assessing and diminishing risk should be developed. The method described in this article is assumed to be a tool for first-level health care to predict severe disabling damage. Early detection of the anatomic predisposition to fracture as well as the identification of osteoporosis shall allow general practitioners to identify patients who are in the femur fracture risk group because of proximal femur geometry pathological changes and to take opportune actions for bone strengthening. This screening approach will decrease morbidity, mortality and the costs required for treatment and rehabilitation. Simultaneously, with a decline in incidence, mortality is also expected to decrease. The plotting methods proposed in this study could also be applied to design mathematical models for preoperative preparations. However, in this way, these methods should be further developed.
What possible argument could I muster18 against that? There was none. Did I eat the peas? You bet I did. I ate them that day and every other time they were served thereafter. The five dollars were quickly spent. My grandmother passed away a few years later. But the legacy19 of the peas lived on, as it lives on to this day. If I so much as curl my lip when they are served (because, after all, I still hate the horrid20 little things), my mother repeats the dreaded21 words one more time: You ate them for money, she says. You can eat them for love.
3. Fountain: In some versions of the story, the fountain is a well. Traditionally, good spirits live in wells, and from thence came the tradition of throwing coins into wells in hopes of having a wish come true (Philip 1997).Return to place in story.
ARTlCLE HlGHLlGHTS
Research background
Currently, a fracture of the femoral neck is a serious health problem, as it very often leads to long-term hospitalization, disability and death of patients. Modern medicine implies the prevention of such serious injuries and their consequences. At the moment, there are methods for assessing bone mineral density, but its geometry remains beyond attention.
Scholars also debate whether the red garment is a hood or a cap according to the earliest versions which more closely translate from the French and German to cap. Return to place in story.
Research motivation
This study was created for the reasons that existing methods often do not take into account the geometric parameters of the bone, and is aimed at filling this gap and creating techniques that complement existing ones.
Research objectives
The purpose of this work was to study the influence of bone geometry on its strength, as well as to find ways to apply these data in practice. The results of the study were conceived as an addition to the existing methods of assessing the risk of fracture.
Research methods
In our study, we measured 70 cadaveric bones and 20 X-rays by creating digital copies of them and processing them in the AutoCAD environment. The cuts of the proximal epiphyses of bones were studied. An analysis was also carried out aimed at identifying parameters correlating with a high risk of fracture. A scale was created as a possible risk assessment tool.
Research results
In our research, we studied the course of bone beams, the distribution of bone tissue in the proximal epiphysis and found the zone that is most vulnerable to mechanical stress. The parameters of the proximal epiphysis were investigated and those that may indicate a higher risk of fracture were identified. A scale was proposed and tested to assess this risk.
And here are two loaves and a sausage; now you won t be hungry! They were tied to the reindeer, the little robber-girl opened the door, made all the big dogs come away, cut through the halter with her sharp knife, and said to the reindeer, Run now! But take great care of the little girl
While I admire the Goose Girl s forbearance, I am not sure I agree that keeping the secret was her best choice. She was forced to make this promise under dishonest and possibly violent circumstances entirely94 against her will. Such a promise should not be kept, especially when it allows an imposter to flourish.
Research conclusions
The geometric parameters of the bone reflect the features of the structure of the bone beams and the distribution of bone matter. There are parameters of the proximal epiphysis, the measurement of which with the help of modern imaging methods can help determine the increased risk of fracture of the proximal epiphysis of the femur. Modern methods of risk stratification often ignore the geometric parameters of the bone and our study suggests a way to take them into account to determine the risks of fracture.
Research perspectives
In order to develop the idea, it is possible to conduct a larger-scale study with a large number of participants. Further refinement of the scale is needed in order to clarify it and possibly expand it. With satisfactory results of refinement, it is possible to introduce the proposed methodology into practice for its clinical trial.
ACKNOWLEDGEMENTS
The authors cordially thank Professor Nikolenko VN (Head of the Department of Human Anatomy, N.V. Sklifosovsky Institute of Clinical Medicine, I.M. Sechenov First Moscow State Medical University) for professional assistance.
FOOTNOTES
Shitova AD, Zubkov DD, Gadzhimuradova IA and Kniazev MO are responsible for measurement of bone parameters; Shitova AD, Olsufieva AV, Zubkov DD, Gadzhimuradova IA and Kniazev MO are responsible for data collection and analysis; Shitova AD, Olsufieva AV, Zubkov DD, Gadzhimuradova IA and Zharikova TS did the literature review; Shitova AD and Zubkov DD graphing in AutoCad2018; Zharikova TS created the figures; Kovaleva ON and Zharikov YO: project manager and scientific advisor.
This study was reviewed and approved by the Ethics Committee of the I.M. Sechenov First Moscow State Medical University (Sechenov University).
The prince let himself be persuaded to go with the nurse, but when the princess questioned him as to who he was and how he had got into her garden, he behaved like a man out of his mind--sometimes smiling, sometimes crying, and saying: I am hungry, Or words misplaced and random61, civil mixed with the rude
Patients were not required to give informed consent to the study because the analysis of the X-ray images and anonymous clinical data that were obtained after each patient agreed to treatment by written consent. Cadaver material (70 femurs) was bequeathed to the Department of Human Anatomy by people and their relatives from 20 to 35 years ago, when these objects were designated for educational purposes for morphological departments.
All authors report no relevant conflict of interest for this article.
No additional data are available.
This article is an open-access article that was selected by an in-house editor and fully peer-reviewed by external reviewers. It is distributed in accordance with the Creative Commons Attribution NonCommercial (CC BYNC 4.0) license, which permits others to distribute, remix, adapt, build upon this work non-commercially, and license their derivative works on different terms, provided the original work is properly cited and the use is noncommercial. See: https://creativecommons.org/Licenses/by-nc/4.0/
Russia
‘My boy, my dear boy!’ cried the king, ‘who is it you want to marry? We will give her to you for a bride, even if she is the humblest of our slaves. What is there in the whole world that we would not do for you ?’
Anna D Shitova 0000-0003-0787-6251; Olga N Kovaleva 0000-0001-7391-5103; Anna V Olsufieva 0000-0003-2115-3287; Inchekhanum A Gadzhimuradova 0000-0001-8922-5086; Dmitry D Zubkov 0000-0002-7251-2422; Mikhail O Kniazev 0000-0002-9155-6236; Tatyana S Zharikova 0000-0001-6842-1520; Yury O Zharikov 0000-0001-9636-3807.
Wu YXJ
A
Wu YXJ
杂志排行
World Journal of Orthopedics的其它文章
- Rates of readmission and reoperation after operative management of midshaft clavicle fractures in adolescents
- Bilateral hip heterotopic ossification with sciatic nerve compression on a paediatric patient-An individualized surgical approach: A case report
- Quantitative alpha-defensin testing: ls synovial fluid dilution important?
- Effect of pelvic fixation on ambulation in children with neuromuscular scoliosis
- Epidemiology of pelvic and acetabular fractures across 12-mo at a level-1 trauma centre
- Higher cost of arthroplasty for hip fractures in patients transferred from outside hospitals vs primary emergency department presentation
