基于改进质心算法的无线传感器网络定位研究

李 昊，柏 植，由 佳，郝保明

(宿州学院 机械与电子工程学院，安徽 宿州 234000)

无线传感器网络(Wireless Sensor Networks，WSNs)是由大量的无线传感器组成的，采用单跳或者多跳的方式完成数据的传输.WSNs可以工作在条件比较恶劣的环境，代替人工进行数据的采集.由于传感器的数量比较多，投放的位置比较复杂，传感器节点的位置确定尤为重要.因此，无线传感器网络定位研究是当今研究的热点问题[1].

无线传感器网络定位算法一般分为两类：基于距离的无线传感器网络节点定位和基于能量的无线传感器网络节点定位.基于距离的节点定位算法需要知道两个节点之间的相对方向和相对距离来确定节点坐标.基于能量的节点定位算法是通过节点的位置移动接收到的相邻节点的能量大小来确定节点的位置[2].其中，基于能量的节点定位算法由于能够减少网络的能量消耗从而达到延长整个网络生命周期的目的而得到了广泛的研究.目前已有的典型算法有：质心法、凸规则定位法、DV-Hop算法、APIT算法和MAP定位算法等.

本文对传统的质心算法进行了改进，提出了一种基于RSSI的改进加权质心定位算法，提高了节点的定位精度.

1 无线传感器网络

无线传感器网络是一种新生的不需设备支持的网络系统，一般由许多汇聚在监测区域的传感器节点和在区域附近的汇聚节点构成[3].虽然传感器节点所占空间小，但是它在这里担着重要角色，例如数据收集器、数据传输站或簇头节点.它们身上配有传感器、处理器和收发器，可以接收信息、处理信息以及向汇聚节点传送信息.互联网将收到的信息整合后发送到用户终端[4].无线传感器网络基本结构图如图1所示.

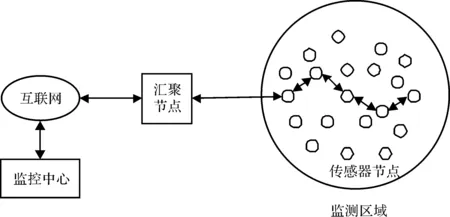
图1 无线传感器网络基本结构图

无线传感器节点的四个部分如图2所示.感知模块中的传感器根据接收的现象产生信号，模/数转换器将信号转为仅表示大小的信号传到处理模块.信息处理模块负责处理传来的信号，并保存到存储器中.无线通讯模块将信号转为模拟信号再发送出去，与其他传感器节点取得通信[5].电源模块是为整个节点供电的模块.另外，针对实际问题中不同的需求，传感器节点还可以添加其他所需的模块.

图2 无线传感器节点的构成

无线传感器网络一般采用单跳或者多跳的方式完成数据的发送.单跳网络结构是指每一个传感器的节点都可以直接将信息传送给汇聚节点，如图3所示.但是，节点用于通信所耗费的能量太多，为了不浪费能量、最大限度提高网络寿命，务必要降低传送的数据量，并且发射距离也要进行相应的缩短[6].多跳的传输方式可以有效地解决能量消耗过多的问题，传感器节点不再单独直接将信息传给汇聚节点，而是发送给彼此连接的网络中间节点，由它们再将信息传给汇聚节点，多跳网络结构如图4所示.

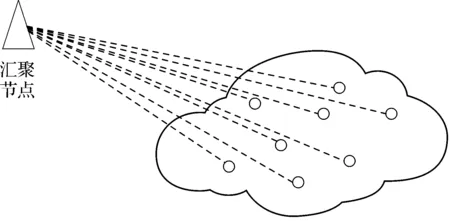
图3 单跳网络结构

图4 多跳网络结构

2 传统质心定位算法

2.1 传统质心定位算法概述

基于距离无关的定位是根据网络连通性来完成定位估量，无需额外配备设备.本文以质心定位算法为论述重点.

质心算法原理图如图5所示，盲节点P(x,y)可以接收并记录来自锚节点A(x1,y1)、B(x2,y2)、C(x3,y3)、D(x4,y4)、E(x5,y5)发送的信息，通过式(1)求解可得盲节点坐标.

图5 质心算法原理图

(1)

由以上内容可知，质心法有优点也有缺点，优点是算法简易，延展性好，但定位精度低，取决于锚节点在范围内的分布数目，并不是十分的精确.未知节点获取位置信息，将高度连接的信标节点添加到集合中，所有连通的信标节点都以其位置作为圆心，距离为半径作圆，则需要知道位置信息的节点就在圆的交集中.质心法只用到信标节点的数据，所以它的复杂度是由信标节点的密度决定的，具有可扩展性[7].

在遇到实际定位问题时，参考节点存在着分布不均的问题，那么如果采用质心法，误差是肯定存在的.当节点均匀分布或者信标节点数量足够多时，定位的精度好，消耗也相对较高[8].相反，定位精度低，成本也低.因此，本文的研究重点是在不增加大量消耗的前提下提高定位的精度.

2.2 传统质心定位算法仿真与分析

研究给出一个固定的区域，然后保持通信半径或者节点数其中一个指标不变，另一个指标进行变化，根据仿真图分析定位误差的变化情况.

首先，给定了一个100*100 m2的监测范围里节点随机分布，其中有部分锚节点以及一个未知节点，且未知节点与信标节点之间的通信半径一样，均为R.

(1)半径为20 m时，由图6可看出，信标节点与总节点的比例增加，定位误差随之降低，后变化缓慢.节点总数为500的定位误差比节点总数为100和300的定位误差要小，说明半径为一定值时，节点数递增，精确度更高.

图6 平均定位误差与节点总数关系图

(2)当节点总数为100个，半径分别为10 m、30 m、50 m时.由图7可得出，半径愈大，其定位误差愈小，在本次仿真中半径为50 m的定位误差最小.锚节点的数目增加，其与总节点数比例越大，定位误差则越小.

图7 平均定位误差与节点通信半径关系图

3 基于RSSI的改进加权质心定位算法

质心定位算法由于其信标节点数量的不同和分布不均，定位产生的误差是不可规避的，相比之下，成本高的测距算法就有较高的定位精度[9].针对这两种算法的优缺点，本文提出了一种基于RSSI测距的加权质心算法，定位精度得到提高的同时，成本不会超出预算.

3.1 RSSI的测距模型

在节点定位中，通过三边测量法，未知节点能通过接收到与其通信的锚节点传来的位置信息算出自己的坐标.三边测量法示意图如图8所示.

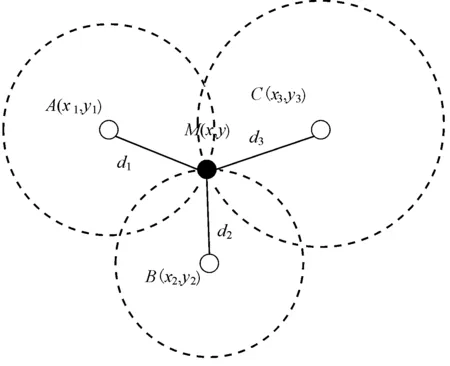
图8 三边测量法示意图

假设未知节点M的位置为(x,y)，令已知的三个信标节点A、B、C的坐标分别为(x1,y1)、(x2,y2)和(x3,y3)，它们距离能够通信的未知节点M的间距为d1、d2和d3.由已知信息可得：

(2)

由下式可算出节点M的坐标：

(3)

但是，非理想情况下，由于环境因素的影响，导致误差的存在，以三个锚节点为圆心、距离为半径画的三个圆不一定交于一点，例如图9，这时候上述方程组在阴影区内能求得出解，且三个圆相交部分的面积越大，定位精度就越低，所以这个方法不是很常使用.

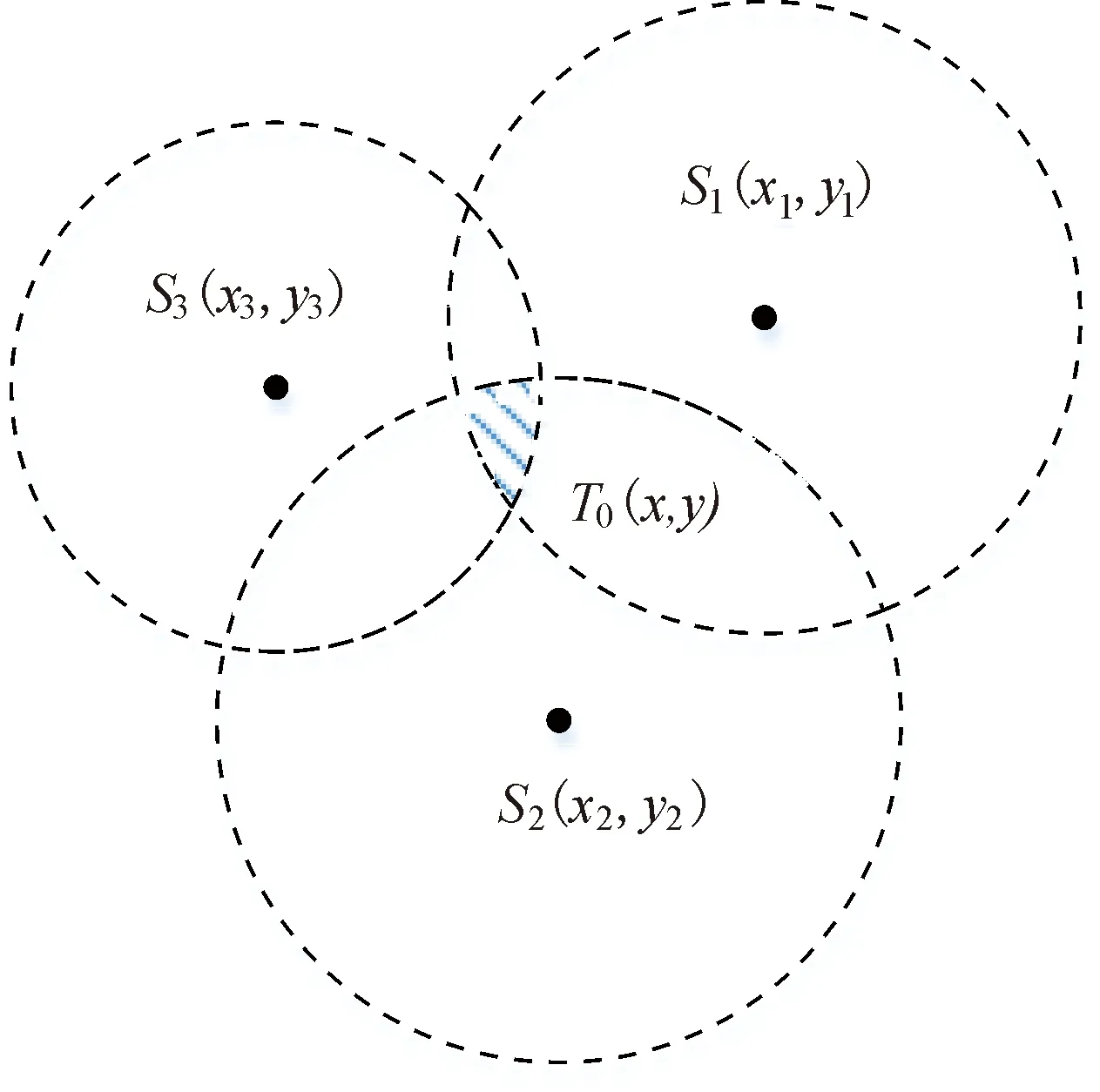
图9 非理想情况下的三边测量法示意图

基于RSSI测距定位的流程图如图10所示.

图10 基于RSSI测距定位流程图

接收的信号强度指示，即RSSI，是依据能进行通信的信号能量的强度来判断间距[10].RSSI值的大小依赖于距离，节点之间的距离可以使用信号和距离之间的衰减模型来计算.在信号发送过程中，若距离过大或者存在障碍物等影响，RSSI值会有误差.所以，从相同的时间间隔内采样得出七组数据，并计算出其算术平均值.

(4)

当应用于现实时，电磁波传输过程中会有损耗，其实际值与理论值会产生偏差.其损耗公式为：

(5)

(6)

其中d0为确定距离；d为接收端和发射端的间距；RSSI(d)指从接收端到发射端这段距离能产生的信号强弱值；RSSI(d0)指离发射端的距离为已知间距时获取的RSSI值；ε和k是系数，为一定值.

3.2 基于RSSI的加权质心定位算法基本思想

由于传统的质心算法只能对与未知节点产生通信的节点坐标进行平均，与未知节点不能产生通信的信标节点的位置信息考虑不到，并且从节点接收到的信息不能得到完全的利用.因此，在改进的时候，注意信标节点在不同点上对未知节点坐标的影响.

将接收信号强弱的值转变为距离，对节点的影响和距离是一对相反的参数，距离增加，对未知节点的作用减小，反之亦然.因此，在传统质心定位算法中加入1/d的权值，形成一种加权的定位算法.

基于RSSI的加权质心定位算法流程图如图11所示.

图11 基于RSSI测距的加权质心定位算法

改进后的加权质心定位算法的公式如下：

(7)

3.3 仿真环境步骤及结果分析

仿真给出100*100 m2的固定监测区域，分别改变节点的通信半径或锚节点数目来观察改进后的质心定位算法随着指标变化而变化的情况.

(1)当节点总数为100时，对信标节点数为8、14和20分别进行仿真.仿真图12表明，当通信半径取一定值、信标节点n=8时，其平均误差为8.16，比信标节点为14和20时分别高出1.56和2.26.说明锚节点数多其定位误差小，通信半径增大，定位误差也逐渐增大.

图12 节点通信半径不同的定位误差

(2)节点总数为100，对通信半径分别为10 m、30 m和50 m时进行仿真.如图13，锚节点的数目增多，误差减小并趋于水平.当通信半径为10 m时，其平均定位误差为9.6 m，比通信半径为30 m和50 m要高.可得半径越大，定位精度依赖于锚节点数目增多而提高.

图13 锚节点数目不同的定位误差

单独对基于RSSI加权的质心法进行Matlab仿真，结果如图14所示.可以看出当参考节点之间的距离比较近时，它的平均误差率随着距离的增加降低幅度显著,距离逐渐增加时，误差也跟着增加.从图15可以看出间距较小时，预测位置与实际位置相差无几.但是，当间距超过一定值时，平均误差率随着间距的增加而增加，预测的位置和实际位置偏差变大.

图14 改变距离对平均误差率的影响

图15 改变距离对预测位置的影响

此外，还将传统的质心法和改进后的算法放在一起比较，如图16所示.可以看出两种定位算法在信标节点总数增加到一定值时，其定位误差变化逐渐稳定，是由于信标节点数增多系统达到饱和状态.虽然两者的变化趋向大体相同，但RSSI质心定位算法的定位误差显著低于传统质心算法，证明所提出改进后的算法确实可行.

图16 传统质心法与改进之后比较

4 结语

无线传感器网络节点定位采用传统质心算法定位精度不高，为了提高节点定位精度，本文提出了一种基于RSSI的改进加权质心定位算法.改进算法在测距阶段利用高斯滤波对信号进行平滑处理，将值加权平均处理，将所得的值转变为距离，定位阶段通过改正其权值增加了有效数据的利用率.通过仿真可知，改进的算法节点定位误差更低，定位精度更高.