无线传感器网络中改进粒子群优化DV-Hop算法的研究*

吴建锋，徐振宇，蒋 震

(1.浙江树人大学信息科技学院，浙江 杭州 310015.2.杭州电子科技大学电子信息学院，浙江 杭州 310018)

过去几年中，位置信息在各种无线传感器网络应用中发挥了重要作用。对许多研究者来说，设计高效的定位算法是一项具有挑战性的任务。

大多数以前的算法[3]假设节点部署在规则区域下，以获得针对大多数应用的满意结果，但在现实世界场景中，往往区域是不规则的，带有空洞和障碍物，因此一对传感器节点之间的几何距离并不总是与它们的跳数距离成正比，这破坏了许多现有的无测距定位算法的假设。

文献[5]在DV-Hop算法中利用信号功率衰减修正跳数，但该方法易受到地形限制。文献[5]提出了Rendered Path算法，利用网络的几何特征，以纠正曲折路径的最短距离，但该算法并未考虑节点的分布密度。文献[7]提出了Partiton weighting算法，该算法对锚节点随机分配等级区域，以此区域加权修正距离，但该法在锚节点数量较少时效果并不理想。文献[8]提出的DV-maxHop算法在计算中移除了一些离未知节点较远的锚节点，并没有很好地利用锚节点的有效信息。

为了提高在不规则区域下的定位精度，本文在DV-Hop算法的基础上进一步研究，提出一种无线传感器网络中改进粒子群优化DV-Hop算法。

1 DV-Hop算法及不规则区域下误差分析

1.1 DV-Hop算法

DV-Hop算法的实现主要有三个步骤:

第1步 估计传感器节点和锚节点之间的最小跳数，所有锚节点将向网络中的所有其他节点广播包含跳数和坐标的消息。跳数的值初始化为零，并在每一跳增加1。

第2步 估计每个锚节点的平均一跳距离:

式中:(xa，ya)，(xb，yb)分别是锚节点a和b的坐标，hopab是a和b之间的跳数。

第3步 评估未知节点和锚节点之间的距离。

式中:dau是节点a和u之间的估计距离，HopSizea是未知节点u最近锚节点a的平均一跳，hopau是在第一步中获得的节点a和u之间的跳数。

1.2 在不规则区域下的误差分析

1.2.1 曲折路径

由于障碍物和空洞的存在，会使得节点间通信的路径发生曲折，这样以简单的跳数乘以平均跳距估计的距离会被严重误估，导致精度大幅度下降。如图1(a)不规则区域所示:锚节点A1和未知节点U3之间由于障碍物的影响造成了严重的曲折路径，跳数明显增加，共有6跳，而两个节点之间的实际距离并不大。在图1(b)规则区域中U3到A1只需要3跳，不规则区域和规则区域下跳数相差3跳，这样根据式(2)得到的估计距离误差较大。

图1 区域节点分布图

1.2.2 未知节点坐标计算方法不合理

使用最小二乘法计算每个未知节点的位置。假设区域内有n个锚节点，未知节点的坐标为(xu，yu)，根据锚节点和未知节点的位置关系可得:

将式(3)写为线性方程组AX＝b的形式，并利用最小二乘法求解:

式中:

将式(2)得到的估计距离dau代入到式(4)中，由于dau在估计时就存在不同程度的误差，故用该法求解坐标时容易造成误差累积。而在不规则区域中，类似这样的曲折路径有许多，即使定位算法精度再高也难以得到准确的坐标值，矩阵b的变化必然会引起解的波动。其次，在求解X＝(ATA)-1ATb时，矩阵ATA可能存在不可逆的情况，导致最终无法获得坐标。此外，当网络中锚节点数量较少或锚节点分布不均匀时，也会对定位精度造成影响。

2 改进粒子群优化DV-Hop算法

在上述误差分析的基础上，本文提出了基于临界值的改进粒子群DV-Hop算法(Critical value and improved particle swarm algorithm of DV-Hop，CPDVHop)来提升不规则区域下的定位精度，在DV-Hop算法的跳数上设置了临界值，对每跳距离进行修正，并用改进PSO代替最小二乘法优化定位。

2.1 曲折路径的跳数与跳距修正

由于不规则区域的影响，锚节点的不均匀分布，无线传感器网络中的跳数与平均跳距各不相同。往往有些未知节点到某一锚节点的跳数远大于正常跳数，为了合理地利用该锚节点的信息，本文设置了跳数临界值限制最大跳数，并对这些超过临界值的跳数相对应的跳距进行了修正，而对于那些小于跳数临界值的信息则不做处理。以此使得未知节点与锚节点之间的估计距离更接近真实值，具体实现方法如下:

步骤1 计算未知节点与其最远锚节点z之间的最大跳数MaxHopu。

式中:N a是网络中所有锚节点的集合，z是离未知节点u最远的锚节点。

步骤2 计算跳数临界值T。当未知节点u的最大跳数超过了临界值T时，代表了最远锚节点z与未知节点u存在曲折路径，需要修正，临界值可以通过文献[9]中的临界值计算公式计算。

式中:R是节点的通信半径，L是网络区域边长，N为节点总数，ρ为锚定比，M是定位未知节点所需的最小锚节点数量。根据式(9)，T一般为3；

步骤3 计算跳距校正值Cau。锚节点通信半径R与平均一跳距离的差值称为最大跳跃距离误差DistErrorMaxHop，由式(10)得到。

不同锚节点相对未知节点的位置不同，最大跳跃距离误差也不同，这里引入加权思想，对最大跳跃距离误差赋以权值，权值λau由式(11)求得。将最大跳跃距离误差乘以最大跳数权值误差得到校正值Cau，如等式(12)所示。

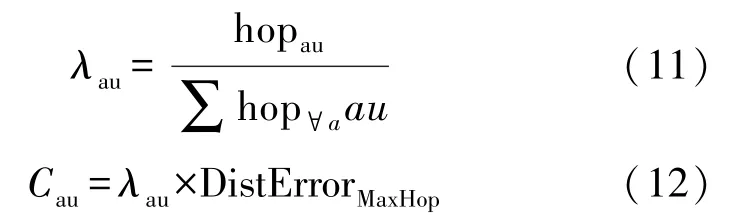
锚节点a和未知节点u之间的每条链路修改后的平均一跳为:

故不规则区域下的估计距离如式(14)所示:

2.2 改进粒子群算法

PSO算法由Eberhart和Kennedy博士提出，其数学模型为:假设粒子种群数为N，每个粒子i包括一个D维坐标和速度向量x i＝(xi1，xi2，…xiD)，v i＝(vi1，vi2，…viD)，粒子i的历史最优位置pb＝(pbi1，pbi2，…，pbiD)，全局最优位置gb＝(gb1，gb2，…，gbD).粒子i的速度和位置更新公式为:

式中:iter表示迭代次数，c1、c2为学习因子，r1，r2为(0，1)上均匀分布的随机数，w为惯性权重。

2.2.1 禁忌搜索

为了解决标准粒子群算法后期局部搜索能力差，收敛速度慢的问题，提出一种改进粒子群算法。首先由粒子群算法实现全局搜索，当算法收敛速度明显降低时停止粒子群算法的搜索，并将当前解作为初始解进行邻域搜索。在邻域搜索法中引入禁忌思想[10]，设置动态禁忌表来禁忌短期内找到的最优解，避免迭代陷入局部最优。当在搜索过程中寻得的解在禁忌表中，则重新生成解。迭代过程中，只有不在禁忌表中的优质解才能作为下一次迭代的初始解。

利用禁忌搜索算法对当前解的邻域做进一步搜索，当搜索次数达到一定次数，而最优解仍未改变时，扩大邻域搜索半径，并增加邻域解数目。当邻域半径扩大数次后，仍未找到比当前最优解更优质的解，则表明该解为当前区域的最优解。

邻域解从当前解的邻域范围rd内随机生成，对于邻域解各维度值均满足:

式中:x′d为邻域解的第d维值，xd为当前解的第d维值。

禁忌对象以目标函数周围区域εi作为禁忌对象，如式(18)所示:

式中:f(x)、f(x′)为当前解、邻域解的目标函数值。

2.2.2 权重改进

ω为控制粒子群算法全局索搜能力和局部寻优能力的主要因素，目前研究采用较多的为线性递减惯性权重策略[11]，通过调整惯性权值来避免陷入局部搜索，本文设置的惯性权重值如式(19)表示:

式中:wmax和wmin分别表示最大和最小惯性权值，并且通常设为0.9和0.4。itermax为最大允许迭代次数，iter表示当前迭代次数，α为(0，1)之间的随机数。

2.2.3 适应度函数

将未知节点到锚节点的实际距离与估计距离的误差作为目标函数:

式中:n为锚节点数量，(xns，yns)为最优解的坐标，(xa，ya)为第a个已知锚节点的坐标，dau为两者之间的距离。fitness值越小，则表示该位置越接近真实位置。

2.3 CPDV-Hop算法过程

①在目标区域随机部署传感器节点，并通过式(2)得到估计距离。

②根据式(7)~(8)得到最远锚节点的跳数与临界值T比较，判断是否存在曲折路径并由式(14)得到修正后的估计距离。

③设置改进粒子群算法相关参数学习因子c1、c2，权重最大、最小值wmax和wmin，种群数N，最大迭代次数itermax，邻域范围ri，禁忌区域εi。

④初始化粒子群。随机产生粒子的速度v i和位置xi，并设置当前最优位置pb和历史最优位置gb，迭代次数iter＝0。

⑤令iter＝iter+1，并根据式(15)和(16)更新粒子速度和位置。

⑥判断是否满足改进PSO算法的终止条件(即达到最大迭代次数itermax)，如果满足终止条件则停止迭代，返回最优解，否则进行⑤。

⑦利用⑥中得到的最优解进行禁忌搜索，如果禁忌搜索得到的最优值优于当前最优值且不在禁忌表中，则更新最优值；若持续找不到最优解，则扩大邻域半径，同时增加邻域解的个数继续搜索。

⑧判断当前解是否满足禁忌搜索迭代结束条件(达到最大迭代次数)，若不满足则返回⑦。反之，输出最优解。

3 算法性能分析

3.1 仿真参数与实验环境

为了验证改进算法的定位性能，在不同的实验条件下对各算法性能进行了对比论证。

采用MATLAB R2016a对算法进行仿真，在二维200 m×200 m区域部署了200个传感器节点，假设所有传感器节点都具有相同的半径R。其半径内的每个传感器节点都能够直接与其所有相邻节点通信。不规则区域布置为“C”、“O”、“S”型，如图2所示。本文算法的参数设置为:学习因子c1＝c2＝2，粒子种群N＝50，最大迭代次数itermax为50。wmax＝0.9，wmin＝0.4，邻域范围ri＝0.01，禁忌区域εi＝0.1。

图2 3种不规则区域下的传感器节点定位

采用归一化定位误差作为定位误差的评价指标:

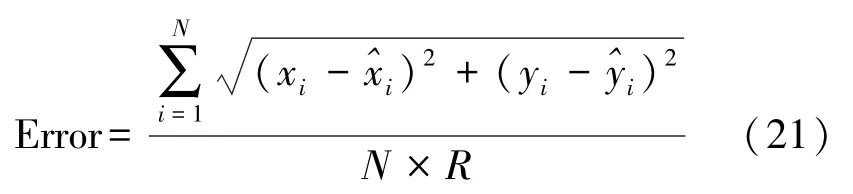
式中:(xi，yi)为未知节点的实际位置，为未知节点的估计位置，N为节点总数，R为通信半径。

3.2 仿真结果及分析

图3是不同定位区域下，节点通信半径对定位性能的影响。设置总节点数为200，锚定比为7.5%。从图中可以看出，经典DV-Hop算法在“C”型网络、“O”型网络、“S”型网络下，定位误差较大，尤其是在“S”型网络下，由于多个曲折路径的存在，定位误差始终高于“C”型、“O”型网络，而“O”型网络接近规则区域，相较于其他网络，受到曲折路径的影响较小，定位精度相对较高。在通信半径为25时，由于未知节点附近可通信得节点数量少，且离未知节点很远的锚节点，跳数值远高于正常值，估计距离过大，故归一化定位精度不高，三种网络模型下归一化定位误差都大于1.5。而在通信半径R＞40时有较好的表现，因为随着通信半径的增大，通信范围内的节点增多，跳数值趋于正常范围。而本文提出的CPDV-Hop算法意在削弱由于曲折半径的存在而导致的估计距离增大，从图中明显可见，本文改进算法，在不规则区域下有较好的适用性。

图3 3种不规则区域下节点通信半径对定位性能的影响

图4~图6分别是“C”型、“O”型、“S”型网络下，不同锚定比，不同节点总数量对定位性能的影响，其中默认通信半径为35 m，节点数量为200，锚定比为7.5%。并与经典DV-Hop，文献[8]的DVmaxHop算法，文献[9]的RDV-Hop算法定位性能进行对比。

图4 “C“型网络下节点数量和锚定比对定位性能能影响的比较

图6 “S”型网络下节点数量和锚定比对定位性能能影响的比较

从图4中可以看出，在“C”型网络下，由于未知节点与锚节点之间存在曲折路径，估计距离误差增大，现有算法的定位精度不高。但当锚节点数和节点数量增加时，四种算法的定位误差均减小，主要是由于锚节点的增多使得未知节点能得到更多有效的跳距信息，而节点总数的增多会减少最小跳数。本文提出的CPDV-Hop算法相较于经典DV-Hop算法、DV-maxHop算法、RDV-Hop算法，在不同节点总数下，定位误差平均减小了53.9%、29.6%和19.7%。在不同锚定比下，定位误差平均减小了48.7%、7.9%和24.4%。

从图5中可以看出，d“O”型网络下，由于存在较少的曲折路径，总体的估计距离误差不大，进而定位误差也不大。随着节点总数的增加，节点间的距离减小，当达到200个节点总数时，定位误差减小幅度趋于平缓。锚节点数增加到15%时，未知节点得到的有效信息达到饱和，定位误差减小趋于平缓。在不同节点总数时，CPDV-Hop算法相较于DV-Hop算法、DV-maxHop算法、RDV-Hop算法，定位误差平均减小了74.1%、36.4%和18.2%。在不同锚定比情况下，定位误差平均减少了57.8%、18.3%和30.5%。

图5 “O“型网络下节点数量和锚定比对定位性能影响的比较

从图6中可以看出，在“S”型网络下，整体定位精度不佳，且在改变节点总数和锚定比时，定位误差减小缓慢，这是由于在该网络下存在较多曲折路径，使得未知节点与最远锚节点之间的跳数明显增加，从而导致估计距离与实际距离的偏差较大，最终导致整体定位效果不佳。本文提出的CPDV-Hop算法在跳数阶段设置了临界值并对跳数进行了修正，定位精度优于DV-Hop算法、DV-maxHop算法、RDVHop算法，在不同节点总数时，定位误差分别减少了51.9%、31.0%和38.5%。在不同锚定比情况下，定位误差分别减少了45.5%、14.6%和24.6%。

4 结束语

本文对DV-Hop算法在不规则区域下的定位误差进行了分析，并提出了改进粒子群DV-Hop算法以优化无线传感器网络定位精度，算法主要做了以下几个方面的改进:①根据不规则区域设定跳数临界值，并判断是否有曲折路径。②利用最大跳数MaxHop修正距离，使得估计距离更加接近真实情况。③引入改进粒子群算法代替最小二乘法对定位结果进行优化。仿真表明，在不规则区域下，CPDVHop比DV-Hop算法、DV-maxHop算法和RDV-Hop算法定位精度更高。