基于ALIF多尺度样本熵和CNN的螺栓组松动定位*

张世壮王 涛*谭波海袁 锐

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉 430081；2.武汉科技大学机械传动与制造工程湖北省重点实验室，湖北 武汉 430081；3.武汉科技大学精密制造研究院，湖北 武汉 430081)

螺栓联接广泛应用于机械、土木等工程领域中，其联接状态对整个工程结构的安全性和可靠性有着重大的影响。在实际工程应用中，结构常常以螺栓组进行联接。当螺栓组中螺栓发生松动时，逐个检测工作量大，但是，如果没有及时检测出来，会加速整个螺栓组的松动从而造成严重的工程事故甚至人员伤亡。因此对螺栓组中松动螺栓进行有效定位具有重要的应用意义。

目前，常见的识别螺栓松动的方法主要分为基于振动的方法[1]、基于压电阻抗的方法[2-3]和基于超声波的方法[4-6]。基于振动的方法适用于识别结构整体的损伤，而不是螺栓松动这种局部缺陷。基于压电阻抗的方法受环境影响严重，在实际应用中效果不稳定。基于超声波方法因其精度高、识别范围大且方便实现而备受关注。但是目前基于超声波的方法常以信号的能量作为健康指标，而信号能量会随着螺栓的预紧力变大而逐渐饱和[7]，对螺栓早期松动定位有一定局限性，并且单个螺栓松动引起的能量衰减在螺栓组中作用较小。目前的研究主要针对单个螺栓对其松动程度进行监测，所用的方法不适合应用在更复杂情况的螺栓组上，在实际工程中应用时会受到限制。对多螺栓形成的螺栓组中松动螺栓的定位研究较少，需要进行更深入的研究。

超声导波通过螺栓联接处会产生非线性特征[8]，这些特征也可以用来定位螺栓的松动。为了提取超声波通过螺栓后的非线性特征，基于熵的方法开始被应用到螺栓监测领域，如近似熵[9]、样本熵[10]、模糊熵[11]等。其中样本熵是基于近似熵优化所得，用来衡量信号的复杂特性并且弥补了近似熵匹配自身的缺陷。Costa[12]在样本熵的基础上，提出了多尺度样本熵(Multiscale Sample Entropy，MSE)。MSE考虑了多个尺度因子下信号的复杂性，克服样本熵单一尺度分析的不足，使信号分析的结果更全面、更准确。之前研究[13]表明多尺度样本熵可以有效地分类螺栓松动情况，能够作为量化信号中非线性特征的指标。

压电主动传感法接收到的信号含有噪声等其他成分，并且螺栓松动处的非线性特征往往隐藏于信号部分成分中，因此需要对数据进行解耦。常用的分析方法如经验模态分解(Empirical Mode Decomposition，EMD)[14]、集成经验模态分解(Ensemble Empirical Mode Decomposition，EEMD)[15]和自适应局部迭代滤波(Adaptive Local Iterative Filtering，ALIF)[16]等已经有效应用于结构健康监测领域。其中EMD能对复杂的信号进行解耦，但存在模态混叠现象；EEMD引入了高斯白噪声，减少了模态混叠现象，但是噪声增大了信号重构误差；ALIF是一种基于迭代滤波的分解算法，能将信号分解成不同分量，具有很好的抗模态混叠能力，被广泛应用于非线性信号特征的提取。葛红平[17]研究表明ALIF在信号分解能力以及模态混叠抑制能力等方面均具有一定的优势。

为实现螺栓松动的有效定位，需进一步对提取的特征进行识别分类。卷积神经网络(Convolutional Neural Network，CNN)自提出以来，不仅应用于图像识别领域，也广泛应用于故障诊断领域。然而如何将一维时域信号进行特征提取转换为二维特征矩阵，是目前基于CNN进行结构健康监测的热点。谷玉海等[14]将各类轴承数据转化为二值化图像作为CNN的输入。陈仁祥等[18]利用离散小波变换时频图提取故障信号二维特征矩阵作为输入。

针对螺栓组的松动定位问题，本文基于ALIF和MSE提出了一种新的分析方法来提取螺栓松动处的二维非线性特征。在ALIF的作用下，响应信号被分解成若干个本征模态函数分量(Intrinsic Mode Function，IMF)，利用相关系数筛选出部分有效的分量并去除冗余分量；然后分别计算每个分量的MSE构成二维特征矩阵；最后采用CNN对特征矩阵进行分类和识别，从而完成对螺栓组松动螺栓的有效定位。

1 ALIF多尺度样本熵和CNN的螺栓松动定位框架

螺栓组松动定位检测原理如图1所示。压电材料分别粘贴在螺栓组的两侧，PZT1、PZT2分别作为激发器与传感器。在一定条件下，包含时变性边界条件的螺栓联接结构在混沌激励作用下会表现出非线性混沌特征，且非线性信号对于早期松动更为敏感，因此本文采用混沌信号作为激发信号作用在PZT1上。数据采集设备从PZT2上接受到响应信号后，做进一步的信号处理。

图1 螺栓组松动定位系统框图

本文结合ALIF和MSE开发了一种新的方法，能够从响应信号中提取特征并通过CNN对特征进行分类识别，实现对螺栓松动的定位。图2为该方法的流程图，详细步骤如下:①用ALIF算法对采集到的各类螺组松动情况的非线性响应信号进行分解，得到若干个包含原始信号信息的IMF分量，然后根据相关系数选择n个合适的IMF分量。②分别求每个IMF分量的多尺度样本熵，并计算前n个尺度因子下的熵值，从而提取出大小为n×n的二维特征矩阵。③将得到的特征矩阵按照合适的比例随机划分为训练集、验证集和测试集，并将训练集和验证集的数据输入到CNN中训练，同时在训练过程中优化、调整超参数，得到一个识别效果好的神经网络模型。④将训练好的网络模型对测试集数据进行测试，得出定位螺栓组中螺栓松动的结果。

图2 ALIF-MSE-CNN螺栓松动定位方法流程图

在实际工程中应用此方法时，可以在安装螺栓组进行联接时提前对目标螺栓组的不同松动情况进行数据采集作为数据库，进行训练得到定位螺栓松动的神经网络模型，之后需要对螺栓组进行松动定位时，可以采集螺栓组当时工况下的信号并用训练好的模型进行识别来定位出螺栓的松动。因此，该方法具有较好的可实施性和移植性。

1.1 自适应迭代滤波分解

Cicone[19]在2014年提出的ALIF是基于迭代滤波(IF)的一种新的模态分解算法。ALIF与IF的区别在于IF采用固定的滤波函数，当遇到非平稳信号时，分解得到的IMF的平滑性无法保证。而ALIF采用Fokker-Planck方程的基础解系作为滤波函数，该函数能够随着滤波区间变化而变化，使分解得到的IMF分量更加精准，实现非平稳信号的自适应分解。

ALIF算法的信号筛选过程主要包括了两个迭代循环，其中内循环用于找到所有的IMF分量，外循环用于提取所有的IMF分量，内循环与外循环均有停止迭代的条件。

1.2 多尺度样本熵

为了从分解得到的IMF分量中提取非线性特征，本文采用了多尺度样本熵。该方法是Costa等人[12]在样本熵的基础上改进所得，具有较强的抗干扰和抗噪声能力。MSE详细计算步骤如下

①对于分解得到的IMF分量imf(i)，i＝1，2，…，N，利用以下公式定义粗粒化序列y(τ):

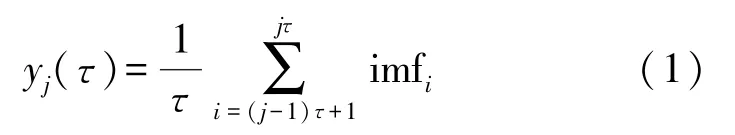
式中:τ为尺度因子，1≤j≤N/τ。

②计算不同尺度因子τ下粗粒化序列y(τ)的样本熵值，即多尺度样本熵:

式中:v为嵌入维数；R为相似容限；ESE为样本熵值；和分别为粗粒化序列的v维、v+1维空间向量个数。

1.3 卷积神经网络

卷积神经网络的结构由输入层、卷积层、池化层、全连接层和输出层组成。原一维数据经ALIF与MSE处理后转化为二维数据输入，通过对输入数据进行一系列的卷积、池化以及非线性激活函数映射等，从原始数据中提取到更抽象的深层特征。经过卷积和池化过程后，数据进入到全连接层。该层中的每个神经与前一层的所有神经元进行全连接，将卷积层和池化层提取到的特征信息进行整合，同时为了避免过拟合的发生，会在该层中引入丢失数据方法(Dropout)。最后全连接层的输出将传入到输出层，完成特征域到样本类别域的映射。

2 实验研究

根据压电主动传感法的基本原理，实验设计如下。实验试样如图3所示，样件材质为铝，尺寸大小为250 mm×30 mm×5 mm，上面有三个M1螺栓，分别表示为B1、B2、B3。两个尺寸大小为8 mm×7 mm×1 mm的压电片分布在螺栓组两侧，其中PZT1作为产生激励信号的作动器，PZT2作为采集信号的传感器。压电材料的压电常数d33＝400×10-12C/N。

图3 实验试样示意图

实验装置如图4所示，其中信号采集/控制设备NI PXIe-1082包含了NI PXIe-5423激发模块和NI PXIe-5172采集模块。本文选择Lorenz混沌方程中的状态变量x作为实验的激励信号。Lorenz方程为:

图4 实验装置

式中:σ＝10，b＝8/3，r＝28。

激励信号采用四阶Rungr-Kutta数值积分式(3)得到，典型信号如图5所示，该信号经NI PXIe-5423模块转换为模拟信号。为了确保信号功率足够大，使用TREK 2100HF放大器将激励信号放大50倍，作用在压电片PZT1上产生激励。激励作用在铝板介质后，超声波通过螺栓处后，被压电片PZT2接收并转换为电压信号，由NI PXIe-5172数据采集模块采集并储存到计算机中。

图5 激励信号

实验中，每个螺栓分为松动(部分拧入)和紧固(完全拧入)两种状态。由于B1、B3关于中心对称，本文将螺栓组松动情况分为6种。每种工况代表了不同位置、不同个数的螺栓发生松动的情况，如表1所示。每种松动情况进行多次实验，每种工况下采集90组实验数据。

3 结果处理与分析

3.1 特征提取

不同螺栓组工况下的信号隐藏着不同的非线性特征，六种螺栓组工况的典型时域信号如图6所示。从时域信号图中无法直接分辨出螺栓组各类松动情况，因此需对信号做进一步分析。

图6 6种工况的时域信号图

使用ALIF对采集得到的响应信号进行数据预处理，将其分解为多个不发生模态混叠的IMF分量。参数的设置参照文献[19]，其中设置分解层数为9(不包括残余分量)、停止准则值为4×10-6、遮掩长度调整值设为1.6。螺栓组某一工况(工况1)信号的分解结果如图7所示。

图7 工况1信号的ALIF分解结果图

响应信号分解后得到的IMF分量中有一部分不能有效映射信号的特征，若不筛选出来，会增加后续计算的复杂度，降低该方法的识别效率。为选择出合适的IMF分量，分别求取了每个IMF与原信号的相关系数，如表2所示，相关系数越大的IMF所含的特征信息越多。

由表2可知，模态分量的相关性呈较均匀分布，特征信息不完全集中在单个IMF中。前7个IMF分量与原信号的相关性较大，因此选择前7个IMF分量用来提取特征。考虑到本文卷积神经网络的输入是二维矩阵，因此，分别计算每个IMF的前7个尺度因子的样本熵，构造成7×7的特征矩阵向量。

表2 IMF的相关系数

3.2 CNN超参数设置

卷积神经网络的超参数直接影响着模型的效率和准确率，需要凭借经验和反复试验来调整。经过多次试验，最终本文的卷积神经网络模型主要设置为:两层卷积层，卷积层卷积核尺寸为3×3，步长为1，卷积核数目依次为32和64。池化层尺寸为2×2，池化方式为最大池化。全连接层神经元数目为256，激活函数为修正线性单元(ReLU)，批量处理个数为12，优化器选择Adam，训练迭代epoch次数为500。

重复实验后，每一类螺栓组松动情况采集了90个样本，按照0.6∶0.2∶0.2的比率将其划分为训练集、验证集、测试集。本文采用TensorFlow框架和TensorBoard进行神经网络模型构建和结果的可视化。

3.3 实验结果

为了研究本文提出方法的有效性以及选择IMF数量与识别效果之间的关系，使用ALIF将响应信号分别分解为5阶、6阶、7阶IMF分量，然后分别计算其多尺度样本熵，构造成特征方阵输入到CNN中。为了更清楚地展现该方法定位螺栓组松动的效果，采用混淆矩阵对结果进行可视化，结果如图8所示。

混淆矩阵中纵坐标代表了预测类别，横坐标代表了数据真实类别。矩阵中非对角线元素框内的数值与百分比代表了真实类别与预测类别不相符的个数及概率，例如图8(a)中第2行第5列，数值1代表了实际工况5的18个测试样本进行预测时，被错误预测为工况2的样本数为1，5.6%代表工况5的样本被错误预测为工况1的概率。因此，矩阵中主对角线元素框内表示每一类18个样本中预测正确的个数及准确率。矩阵上方为总体样本识别分类的准确率，即主对角线上准确率的平均值，表示当前方法训练所得模型的定位螺栓松动的能力。

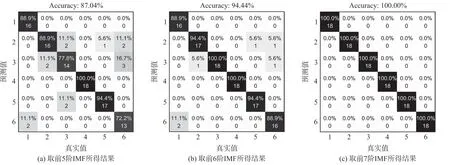
图8 实验结果图

由结果图可知，输入的特征矩阵取前5阶IMF分量时准确率为87.04%，取前6阶IMF时准确率为94.44%，而取前7阶时准确率可以高达100%。这表明该方法可以有效提取映射螺栓组松动的非线性特征，并且能够精准分类出螺栓组不同的松动情况。只选取部分IMF阶数时，提取的特征矩阵无法完全反映螺栓松动处的特征，导致分类识别的准确率低。随着选取IMF阶数的增多，分类识别的准确率逐渐变大，验证了本文之前通过IMF与原信号的相关系数作为选取依据的正确性，使该方法具有自适应性。对IMF阶数进行筛选不仅减少了模型的复杂度和后续的运算时间成本，而且增加了该方法在实际应用中的可实行性。

3.4 对比实验

为了证明本文提出的特征提取方法的可行性与优越性，使用本文实验数据，分别选择EMD、EEMD两种分解算法以及将原始信号直接输入一维CNN的方法进行对比验证。两种分解算法分别取前7阶IMF分量与多尺度样本熵进行多维特征提取，并用CNN对比分类识别的准确性。采用EEMD时，设置总体平均次数M为100，高斯白噪声的标准差为原信号的0.25倍[15]。一维CNN结构的搭建和参数的选择根据文献[20]进行。重复多次试验后，四种方法10次结果及训练时间对比如图9和表3所示。

图9 准确率对比图

表3 训练时间对比

从结果可知，三种采用了信号分解的方法都有着不低的准确率，验证了这种特征提取思路的正确性。ALIF和EEMD分解后的第三阶IMF分量及其放大部分如图10所示，可见ALIF的分解能力和抗模态混叠能力更好。因此，其识别结果的差异是由算法处理信号能力的不同引起。与直接使用一维CNN的方法对比，本文提出的方法有着更高的准确率且训练时间少，可见对数据进行特征预提取可以加强CNN的学习能力和速度，更能有效地定位出螺栓组的松动。并且本文提出的方法10次实验结果的波动小，这意味着该方法有着良好的鲁棒性。

4 结论

为定位出螺栓组的松动螺栓，本文提出了一种基于自适应迭代滤波和多尺度样本熵进行多维特征提取，然后用卷积神经网络进行识别的方法。本文所得主要结论如下:①将ALIF和MSE相结合来提取螺栓组松动处的特征。ALIF可以将信号进行自适应分解，有效地分离出信号中重要的部分。MSE可以映射螺栓松动处的非线性特征。两者相结合可以有效提取螺栓松动处的非线性二维特征矩阵。CNN结果证明了该方法的有效性，并且相较于其他方法，有着较高的准确率和较好的鲁棒性。②信号分解后，依据IMF与原信号的相关性来选择合适阶数的IMF分量，增加特征信息的同时，减少了后续操作的复杂度及成本，使该方法具有自适应性。③基于压电主动传感法，采用混沌非线性激励信号对M1小螺栓组的松动情况进行了有效定位，结果显示该方法实施简便、精度高、适用范围广，具有好的应用价值。

本文为定位螺栓组松动提供了一种新的分析方法，实验表明该方法具有较好的识别精度和应用前景。但该方法仍有大量工作需要更深入研究，如螺栓松动程度的定量识别、更加复杂螺栓组的松动螺栓定位以及工程实际应用问题等。