自确认气动执行器的故障诊断算法研究*

冯志刚，杨佳琪

(沈阳航空航天大学自动化学院，辽宁 沈阳 110136)

执行器作为工业自动化控制系统的终端执行部件，可分为气动、液动与电动三大类。气动执行器基于自身材料和结构等因素而被广泛应用。但当气动执行器由于某种原因性能下降或者发生故障时，控制输出将偏离理想输出，易造成人员伤亡或财产损失等。因此，气动执行器故障诊断技术对于维持控制系统的稳定性至关重要。针对气动执行器的故障诊断问题，文献[1]基于MVRVM回归原理提取残差特征作为关联向量机(Relevance Vector Machine，RVM)二叉树分类机的输入，诊断气动执行器故障类型。文献[2]通过分析故障数据的主元向量，建立PLS模型，采用Hotelling T2和SPE统计方法对故障诊断结果进行验证，但识别故障类型少，识别精度不高。文献[3-4]主要采用神经网络和支持向量机(Support Vector Machine，SVM)方法，但SVM核函数受Mercer条件限制，且核参数选取困难，而神经网络算法收敛速度慢、需要样本数量多及容易陷入局部最优，影响故障诊断的准确度。同时由于执行器是闭环控制系统，有反馈的影响，传统的故障诊断方法不能有效地在整个系统性能下降到不可接受之前完成执行器的故障诊断。因此，本课题组基于对原有三组件式气动执行器的研究，提出了一种自确认气动执行器[5]，尝试应用一种基于自适应多核多分类关联向量机的气动执行器模式识别方法，意在解决气动执行器故障类型的多样化问题，能够直接实现多分类，并采用自适应粒子群算法和遗传算法的混合算法优化组合核参数，从而实现自确认气动执行器的故障检测与诊断。

1 自确认气动执行器结构及常见故障描述

本课题组以气动执行器为研究对象，如图1和图2所示。将执行器接收的控制量作用到阀门定位器，驱动执行机构带动阀杆运动，改变阀芯和阀座之间的流通面积，并将阀杆的位置信号、介质温度、流量、阀前压力和阀后压力信号均反馈到定位器，由此构成闭环控制，以控制调节阀中流体流量[6]。

图1 传统三组件式气动执行器结构图

图2 自确认气动执行器结构图

对于图2所示的自确认气动执行器，其结构模型如图3所示。其中，CV是执行器接收的控制量，即阀位指令信号，P1表示阀体前流体压力，P2表示阀体后流体压力，T1代表阀体流体温度，X代表阀杆位置反馈信号，F为流量信号。CV、P1、P2和T1为自确认执行器模型的输入，X和F为输出。

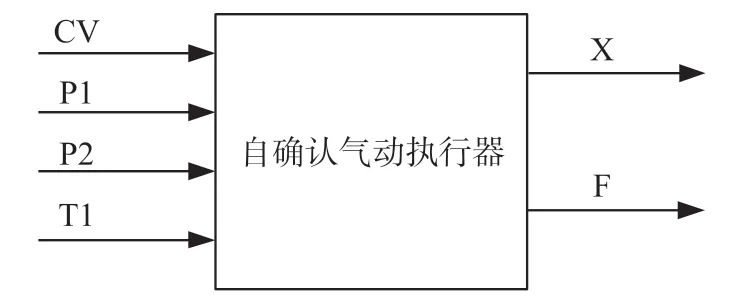
图3 自确认气动执行器模型原理图

当执行器性能受损，给定的各参数无法维持在相应正常的范围，此种状态视为发生故障。关于气动执行器19种典型故障的描述[7]，如表1所示。

表1 气动执行器的19种典型故障

2 基于关联向量机的数据恢复方法研究

2.1 关联向量机回归原理

给定气动执行器的输入和输出训练样本集[8]:表示该执行机构的第n组输入样本向量，N为正常状态的训练样本组数，输出样本向量为y N×1＝[y1，y2，…，yN]T，目标值yn可表示为式(1)，其概率表达如式(2)和式(3)所示:

式中:εn表示误差函数，服从均值为0，方差为σ2的高斯分布，W＝(w0，w1，w2，…，wn)T是模型的权向量，K(X，Xn)为核函数，Φ为核函数设计矩阵。

给定新的一组测试样本集数据X*，则相应目标值y*的预测分布为:

式中:

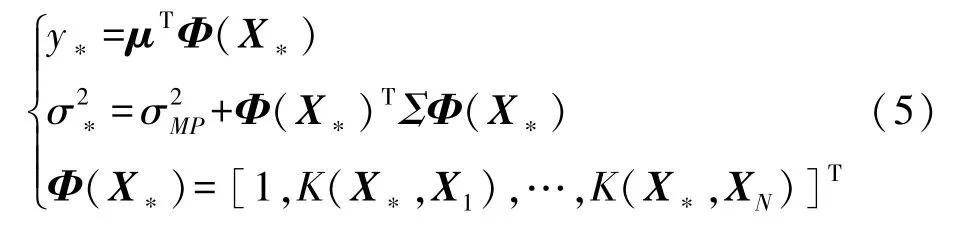
σMP和可通过最大边缘似然函数方法来估计，可得:

式中，μi是均值向量μ的第i个元素，Nii为方差矩阵Σ的第i个对角线元素。具体推导过程请参考文献[9-11]。

2.2 RVM预测器核函数选择及参数优化

由于样本数据分布的不同，选取不同的核函数对预测器的识别精度会产生很大的影响。本文将通过分析线性核函数:k(x，y)＝xTy+c、多项式核函数:p(x，y)＝(a xTy+c)d、高斯核函数:g(x，y)＝和Sigmoid核函数:s(x，y)＝tanh(a xTy+c)对RVM预测器性能的影响，选择最合适的核函数建立预测器模型，并采用k遍历交叉验证方法对核参数进行优化。

2.3 利用RVM实现故障数据恢复及特征提取

故障数据恢复方法的主要思想是利用正常数据的历史样本信息对故障状态时刻点的错误输出值进行最佳预测或估计。本项目组基于关联向量机回归原理的理论知识，利用执行机构的正常数据建立模型，可以表示为式(7)、式(8)，用预测值代替错误输出值实现数据恢复。

将模型预测输出值与实际输出值进行比较，获得残差，将此残差作为识别自确认气动执行器故障类型的特征。根据式(7)、式(8)，可得残差方程:

式中:阀前压力信号P1和阀后压力信号P2的振幅和频率是取合适的正弦信号，执行器接收的控制量CV取合适的定值，每个故障运行200次，每次运行2 000s，最终得到18种故障类型(包括无故障)的3 600个故障样本集。

3 基于多核多分类关联向量机的气动执行器的故障诊断

3.1 多分类关联向量机模型介绍

式中:ycn为Y的第n行l列的元素；wc为W的第l列；kn为K的第n个样本与其他样本的关联性。

通过引入多项概率连接函数将回归目标转换为类标签实现多分类:

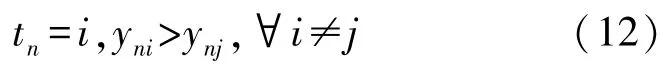
通过多项概率似然函数表示类成员的概率输出:

式中:u~N(0，1)，Φ表示高斯累加分布函数。W中的回归因子，其中αnc为尺度矩阵A∈RN×C的元素，服从超参数q，p的Gamma分布。

采用最大后验定理方法，回归量可推导为:

基于此，给定类的参数可以更新为:

式中:Ac是A的第c列对应的对角矩阵。因此，推导出辅助变量的后验分布，给定类别i，于∀c≠i，有:

先验参数的后验概率分布为:

Gamma分布的均值为:

3.2 多分类关联向量机模型学习

多分类关联向量机采用快速type-Ⅱ最大似然参数法。由边缘似然函数P(WA)dW可以推导出:

式中:C＝I+KA-1KT可以分解为:

式中:C-i表示删除第i个样本后的C值。则有:

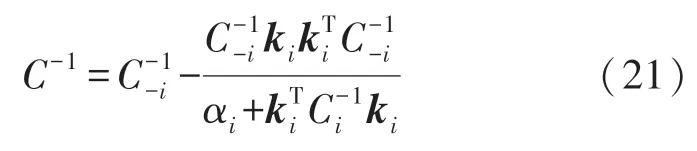
将L(A)进一步分解为:

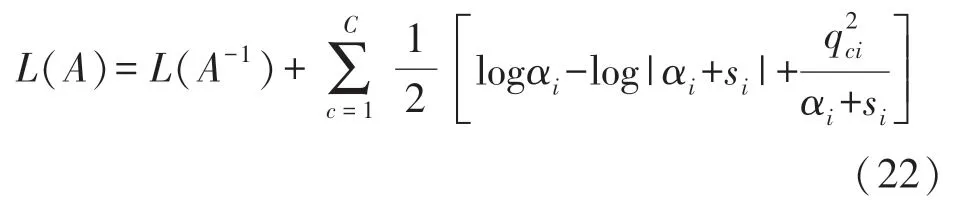
在模型训练过程中，最大后验值更新为:

最后，模型的训练过程从以下初始集合开始:

3.3 核函数选择及参数优化

不同核函数线性组合的数学表达式为:K＝为基本核函数，N为核函数总个数，λj是权重系数，即组合系数。

本文基于高斯核函数和多项式核函数得到最优核组合:

式中:

为了消除人为主观因素的影响，本文采用粒子群(Particle Swarm Optimization，PSO)算法和遗传算法(Genetic algorithm，GA)的混合算法对参数λ、σ、d进行寻优选择[15-17]。多核组合原理如图4所示。

图4 多核组合原理图

3.4 粒子群与遗传算法优化多核多分类关联向量机参数

粒子群算法首先在D维空间中组成一随机初始化的粒子群，通过设定好的群体规模、迭代次数、粒子速度和位置等，对粒子群以迭代的方式逐步搜索最优解，每次迭代过程中，粒子通过个体极值和群体极值更新自身的速度和位置，即:

式中:d＝1，2，…，D；i＝1，2，…，n；k为当前迭代次数；Xi，d表示粒子位置，Pi，d表示个体极值，Pg，d表示群体极值，Vi，d为粒子速度；c1，c2是加速度因子，为非负常数，r1，r2是[0，1]区间内的随机数，ω为惯性权重，影响粒子更新速度，当ω取一个较大的值时，不利于参数的局部寻优，而ω较小时，容易陷入局部最优。因此采用自适应权重法对ω进行改进，依据早熟收敛程度和适应度值进行调整，有利于获得更好的寻优结果:

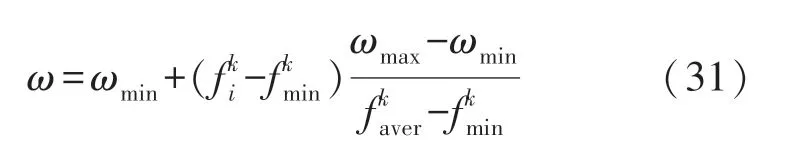
式中:i为迭代特征，k为此刻的迭代次数，f为适应度值。为防止盲目搜索，一般将粒子位置和速度限定在区间[-Xmax，Xmax]，[-Vmax，Vmax]，。

本文在自适应粒子群算法的基本框架上，将遗传算法思想引入其中，遗传算法利用选择、交叉和变异操作，增强局部搜索和全局搜索的能力，通过优胜劣汰的选择机理使整个种群接近最优状态。具体改进方法如下:第一部分，首先初始化粒子相关参数，计算每个粒子适应度函数值，基于个体最优和全局最优更新粒子的位置和速度，预测变异的方向和幅度。第二部分实现对个体进行选择、交叉、变异操作，产生新的子代个体替代父代个体，计算杂交变异后的粒子适应度并不断更新使种群进化。

式中:f为以分类错误率作为优化目标的函数值，n为故障类型的数量，y*(i)为第i个故障类型识别错误率。

粒子群算法与遗传算法结合对多核多分类关联向量机进行参数优化的具体流程如图5所示。

图5 基于PSO与GA算法的多核多分类RVM流程图

4 实验结果分析

基于DAMADICS平台建立气动阀门仿真模型，利用DABLib模块获得了自确认气动执行器每种故障及正常状态各200组数据，选取正常状态数据建立基于关联向量机回归的气动执行器模型，为了分析不同输出特征的核函数性能，对单核RVM故障特征提取，并采用5折交叉验证获得最优核参数值。表2列出了气动执行器的不同故障输出特征的RVM预测器性能。仿真实验均在PC机(Intel(R)Core(TM)i5-8500，8GB内存)上的MATLAB R2018b中运行。

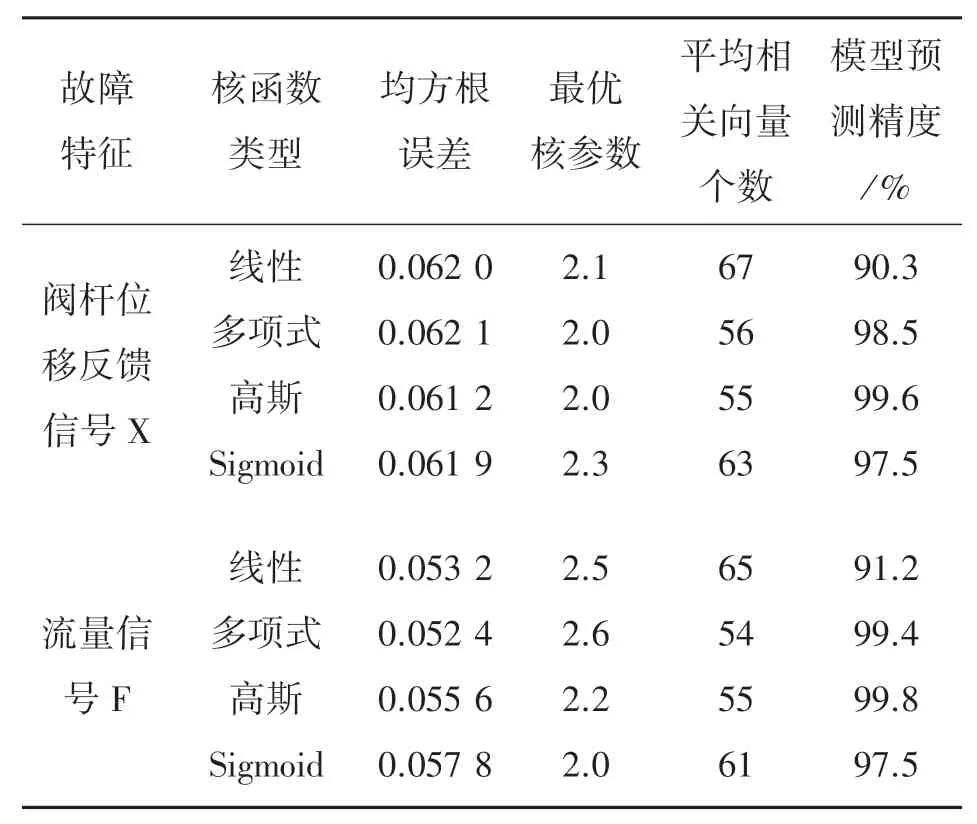
表2 基于不同核函数类型的RVM预测器性能比较

由表2可以看出，不同故障输出特征的核性能有很大差别。经检验，阀杆位移反馈信号X选择高斯核函数，流量信号F选取多项式核函数，预测误差小，相关向量数量少。图6为利用正常数据建立RVM预测模型，对不同输出特征进行数据恢复的结果显示图，并将其余每种故障及正常状态数据样本输入到建立好的气动执行器模型，产生残差，图7至图10是以无故障数据和故障f1，f7，f15仿真数据输出的残差特征为例的波形图，共获得故障样本集3 600组。

图6 利用最优核参数建立预测器的回归结果

图7 无故障仿真数据输出的残差特征

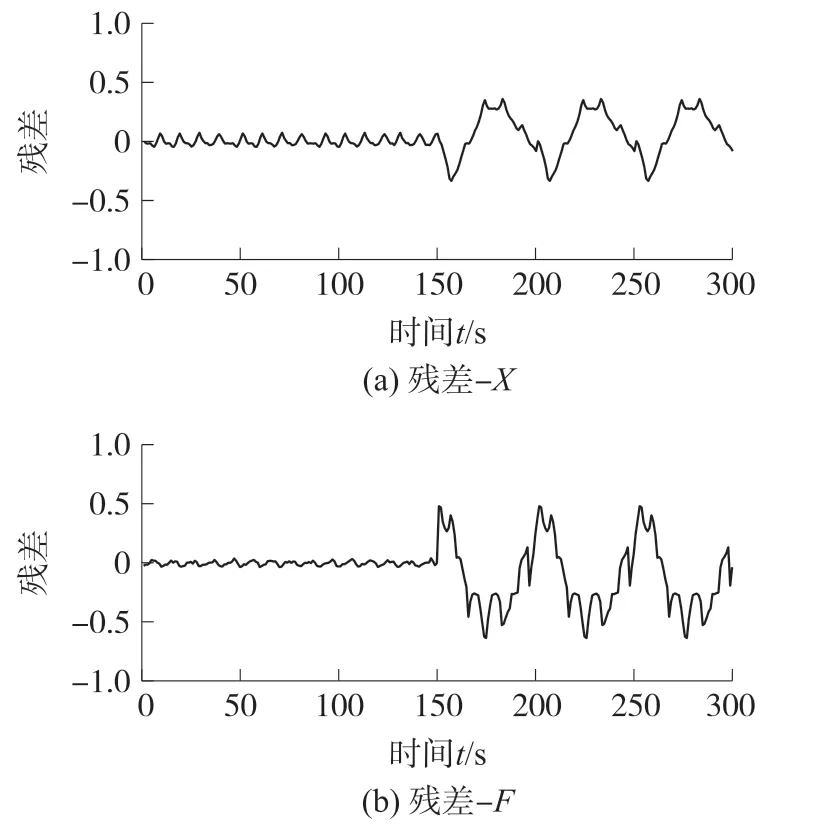
图10 故障f15仿真数据输出的残差特征

文中设定粒子种群数为30，c1＝c2＝1.5，最大迭代次数N＝50，惯性因子最大值ωmax＝0.9，ωmin＝0.4，交叉概率Pc＝0.5，变异概率Pm＝0.02，其适应度随迭代数变化曲线如图11所示，当迭代次数达到17次时，最佳适应度值为0.008 5，该适应度对应的参数为最优值，即λ＝0.3，σ＝1.21，d＝2。

图11 参数寻优过程

任意选取故障样本集1 000组数据用于训练自适应多核多分类RVM分类机，其余的每种故障及正常状态共2 600组数据用于对算法的测试。

图8 故障f1仿真数据输出的残差特征

图9 故障f7仿真数据输出的残差特征

表3给出了详细的训练样本数目和测试样本的故障识别结果。

由表3我们可以看出:f1，f2，f3，f4，f7，f10，f11，f13，f15，f16，f17和fn的所有测试样本均被正确识别，f5，f6，f9，f12，f18，f19识别率均高于95%，采用此种故障诊断识别方法不仅精度高，还可以提高故障类型识别数量。

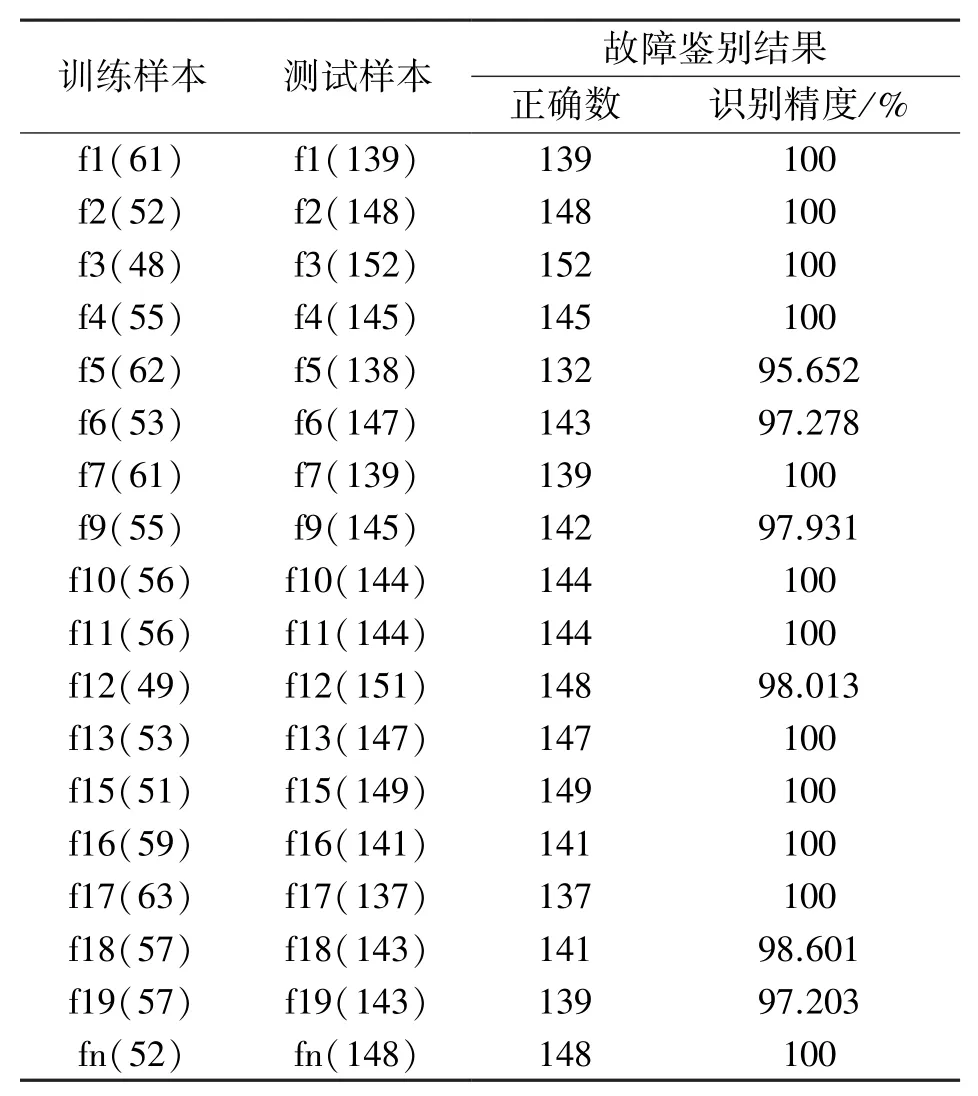
表3 训练样本数目和测试样本的故障诊断结果

5 结论

本文通过分析自确认气动执行器结构及其输入输出之间的关系，提出了一种基于关联向量机回归原理的特征提取方法和基于自适应粒子群融合遗传算法优化多核多分类关联向量机的故障分类方法，利用气动阀故障仿真模型DABLib模型产生不同类型和不同强度的故障数据，对所研究方法进行了验证，共实现了18种故障类型的识别。结果表明，所研究方法对于建立自确认气动执行器模型和实现故障类型多样化分类具有较好的适用性。但是对于渐变性故障，在故障强度较小时，很难及时发现并诊断出故障类型，影响执行机构的性能，这些都是将来需要完善和深化研究的地方。