基于矩阵分解的捷联惯导多位置系统级标定方法*
2022-08-18赵桂玲谭茂林
赵桂玲,谭茂林,吴 偲
(辽宁工程技术大学测绘与地理科学学院,辽宁 阜新 123000)
捷联惯导系统级标定的实质是根据系统的导航输出进行惯性测量单元(Inertial Measurement Unit,IMU)误差参数的估计[1-3]。IMU误差参数标定结果直接影响系统的导航精度,IMU估计精度和标定时间也成为反映系统级标定技术的关键指标[4-5]。常用的系统级标定方法分为拟合法和滤波法[6-7]。拟合法的研究集中在标定路径编排,通过设计合适的标定路径建立起观测量与误差参数之间的关系,再利用最小二乘估计对误差参数进行标定[8]。拟合法路径编排与待辨识误差参数密切相关,计算简便,但标定模型推导复杂[9],标定环境和条件要求严格[10]。
滤波法研究集中在设计滤波方案[11-12],通过建立系统状态方程和量测方程,利用Kalman滤波算法对误差参数进行估计[13],鲜有文献对路径编排进行深入的理论推导和分析,导致标定位置多、标定时间长。文献[14]建立了36维Kalman滤波模型,标定路径为25位置,标定时间约为4 h。文献[15]设计了一组13位置转动编排方案,标定21项误差参数用时约1 h。文献[16]以导航速度误差为观测量建立了27维Kalman滤波器,设计了一组8位置标定路径来标定21个误差参数,标定时间为40 min。上述文献未对误差参数辨识与路径设计进行深入的理论分析和探讨。文献[17]对IMU误差参数激发过程进行分析,建立了27维滤波模型,设计了35次序标定路径,标定时间为2 h,标定路径过于复杂。上述研究均存在标定时间长,标定路径复杂等问题。
针对上述问题,本文将安装误差角分解为不正交角和正交的失准角,建立非正交和失准的标定模型。将拟合法中路径编排与误差参数辨识紧密联系的特点引入滤波法,设计了7位置连续标定路径,对误差参数的可辨识性、可观测强度和标定时间进行分析,完成21项误差参数的完全标定,标定时间小于30 min。
1 系统模型的建立
1.1 IMU输出误差模型
捷联惯导系统通常由三个加速度计和三个陀螺组成,加速度计的比力误差和陀螺的角速率误差为:
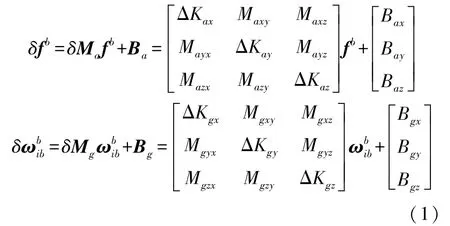
式中:δfb和分别表示加速度计和陀螺的输出误差;δMa和δMg是三阶方阵,两个矩阵中主对角线元素分别表示加速度计组件和陀螺组件标度因数误差,非主对角线元素表示加速度计组件和陀螺组件安装误差;fb和表示IMU理想输出;Ba和Bg分别表示加速度计和陀螺的零偏误差。
导航坐标系下观测量对载体坐标系参数约束不足,加速度计和陀螺12项安装误差系数存在3组耦合关系[18]。将加速度计或陀螺敏感轴进行重新定义,对载体系参数形成约束,安装误差参数降为9项。引入矩阵分解原理[19],将δMa和δMg分解为对称矩阵(Symmetric matrix)与斜对称矩阵(Skewsymmetric matrix)之和。和表示对称矩阵,和表示斜对称矩阵。

加速度计组件和陀螺组件的安装误差特性由非正交特性和正交失准特性构成。非正交特性表现为组件的3个输入轴不正交,正交失准特性表现为正交组件相对载体系失准。采用最佳约束方式使陀螺斜对称矩阵为零[19],对应安装误差标定流程如图1所示。

图1 安装误差标定流程
从式(2)和图1可知,本文对IMU安装误差进行分解,安装误差角被分解为非正交角和正交的失准角。安装误差标定流程为先完成安装误差正交化,正交化完成后的组件相对载体系b系失准,需要转动与b系重合,使IMU完成真正意义上的安装误差建模。由于约束关系的存在,本文设计的约束方式是将正交化后的陀螺组件构成的正交坐标系视为与b系重合。由此,系统输出误差模型设定为:
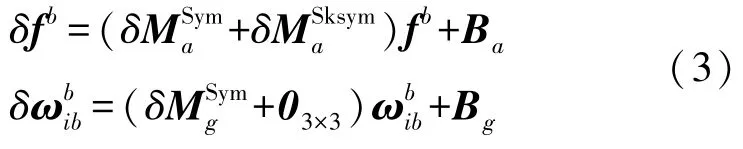
1.2 系统误差方程
忽略δg影响,略去二阶小量,姿态误差角φ=[φxφyφz]T为小角度,静基座下IMU误差参数引起捷联惯导系统速度和姿态误差方程为:

式中:导航坐标系n系选用东-北-天坐标系,载体坐标系b系选用右-前-上坐标系。表示n系下速度误差,fn表示比力在n系下的投影,表示地球自转角速度在n系下的投影,δfb和为系统输出误差模型中b系下比力误差和旋转角速度误差。表示b系到n系的捷联矩阵,静基座条件下fn=(说明:ωc、ωs分别为ωiecosL、ωiesinL的简写,L为当地地理纬度)。
1.3 Kalman滤波模型
根据IMU系统输出误差模型和系统误差方程,建立的Kalman滤波状态变量为27维:

根据式(4)和式(5)构建滤波器状态方程和量测方程:

式中:F为状态转移矩阵,G为系统噪声分配矩阵,W为IMU输出中的白噪声向量,观测矩阵H=[I6×606×21]。
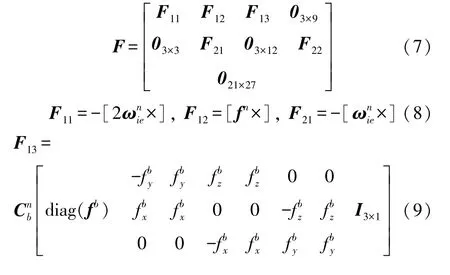

2 标定路径的设计
2.1 路径编排
在静基座条件下,IMU通过敏感重力加速度g和地球自转角速率ωie完成误差参数的标定。由于ωie是一个小量,为更好地激励陀螺各项误差参数,同时保证标定过程的连续性,通过转台施加转动角速率ωr完成位置变换。
1.2.1 对照组 行单一肛瘘切除术治疗:患者手术前进行常规的灌肠和导泻,所有患者进行腰-硬联合麻醉[3],麻醉后进行常规消毒,然后铺巾,等待肛门括约肌松弛舒张后进行肛内消毒。行单一肛瘘切除术治疗时首先探针由外口向内口插入,然后将瘘管和内口沿探针切除,沿着切开的瘘管清除所有瘢痕和坏死组织。对患者术后情况观察并记录。
设计IMU敏感轴在两个标定位置分别指向天向和地向快速消除误差参数中的部分耦合关系。以“北-东-地”和“北-西-天”两个位置为例。在“北-东-地”完成静态导航后,绕x轴转动180°到达“北-西-天”。对于IMU静止在标定位置时,设静止时间从t0~t1,则在静止位置下有:
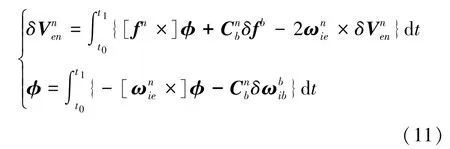
将两个位置对应的参数代入式(11),得两个位置下的速度误差和姿态误差,如下
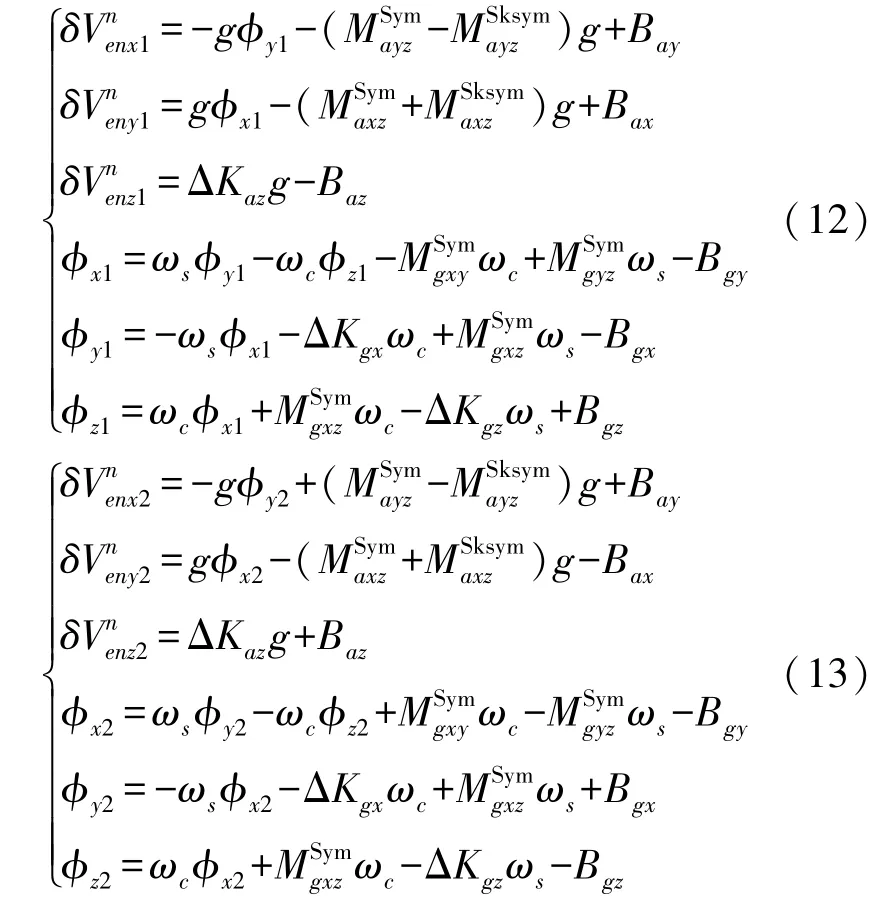
从式(12)和式(13)可看出,两个位置下速度误差和姿态误差对应被激励的IMU误差参数是相同的,参数前的正负号不同,联立公式即可消除参数间的耦合关系。通过这种标定位置设计方式可以快速辨识加速度计和陀螺误差参数,如下:

上述两个标定位置可以直接辨识出7项误差参数,另外有9项误差参数虽被激励,但由于存在耦合关系不能被辨识出,剩下的5项参数则不能被激励。
IMU从“北-东-地”绕x轴旋转180°到“北-西-天”,转台转动角速率ωr设计为6°/s,标定中由于ωc≪ωr、ωs≪ωr,Bgi(i=x,y,z)≪ωr,因此在转动过程中可忽略地球自转角速率和陀螺零偏。在t1~t2转动过程中由陀螺误差引起的姿态误差方程如下:
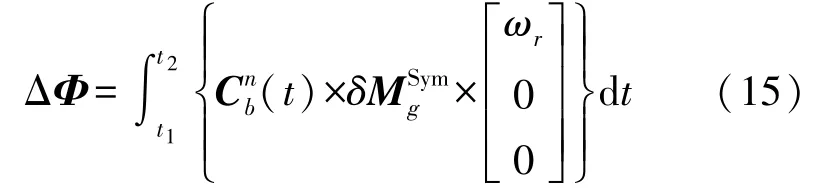
式中:以“北-东-地”为初始位置绕x轴转动,转动过程中的捷联矩阵为:

转动完成后,

从式(17)可看出,本次转动可使陀螺3项误差参数被辨识出。由于Bgi(i=x,y,z)≪ωr,在转动过程中难以辨识,在转台静止时进行IMU零偏标定。零偏仿真结果如图2所示。每个位置静止600 s,转动时间为30 s,标定时间共计20.5 min。
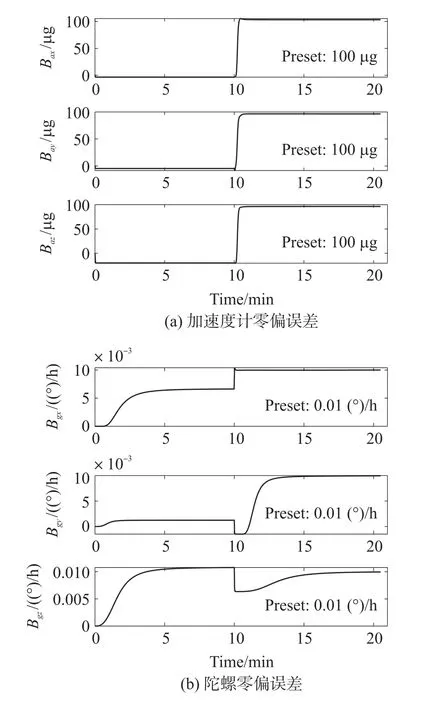
图2 IMU零偏误差估计曲线
2.2 标定方案
同一标定路径下,不同误差参数的可观测度不同。图2中,加速度计零偏误差可观测度高,陀螺可观测度低。当从“北-东-地”转换到“北-西-天”时,加速度计3项零偏误差在很短的时间内达到收敛。陀螺3项零偏误差的可观测度差别明显,Bgx在该路径下可观测度强,短时间即达到收敛,Bgy在转动完成后需要约6min才能收敛,Bgz需要约8 min才能收敛。分析原因,陀螺敏感地球自转角速率是一个小量,导致陀螺零偏的可观测度低,需要的标定时间长。综合考虑加速计和陀螺零偏收敛时间,本文设计标定路径如图3所示,前2个位置静止时间分别为500 s,后5个位置静止时间分别为120 s。
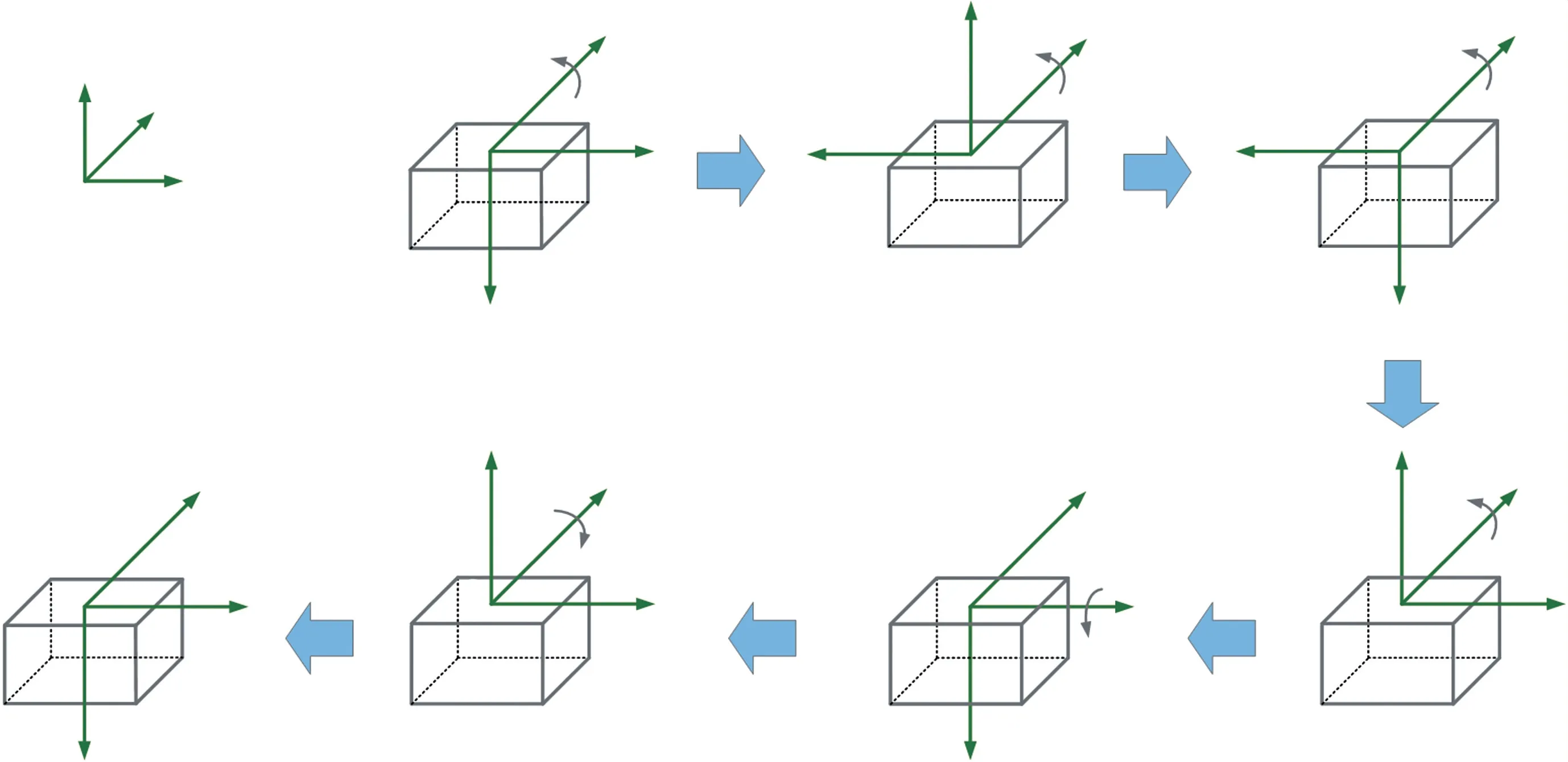
图3 7位置标定路径
2.3 可观测性分析
为验证标定路径的有效性,采用分段线性定长系统(Piece-Wise Constant System,PWCS)对路径进行可观测性分析。利用提取的可观测性矩阵(Stripped Observability Matrix,SOM)代替总的可观测性矩阵,使得模型的可观测分析变得更简单[20]。
根据Kalman滤波器的状态方程和量测方程,可观测性矩阵SOM为:
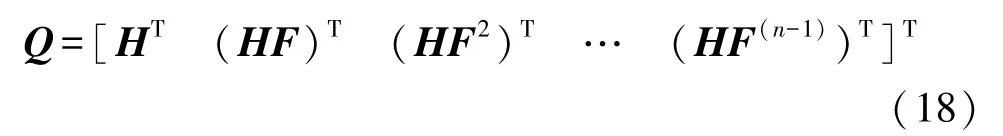
式中:Q代表矩阵SOM,n为Kalman滤波器状态维数,为27维。计算SOM在各位置下的秩,结果如图4。
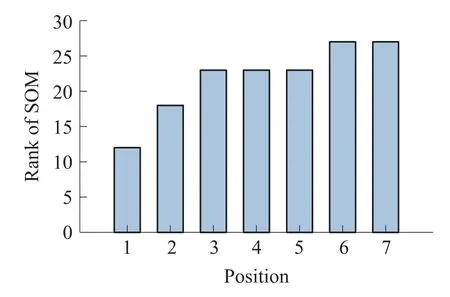
图4 各位置下可观测矩阵的秩
从图4可以看出,系统在第六个位置时,SOM的秩达到27,等于滤波器状态维数。可以判定系统状态在该路径下完全可观测[21],验证了论文设计路径的可行性。
3 实验结果与分析
对7位置系统级标定算法进行仿真实验。初始速度设置为V0=03×1,3个初始姿态角分别设置为:航向角270°,俯仰角0°,横滚角180°,采样频率设置为100 Hz。各误差参数的预设值见表2。滤波估计曲线如图5~图10所示。
从图5~图10中可以看出,各误差参数都能完全收敛,估计结果见表1。
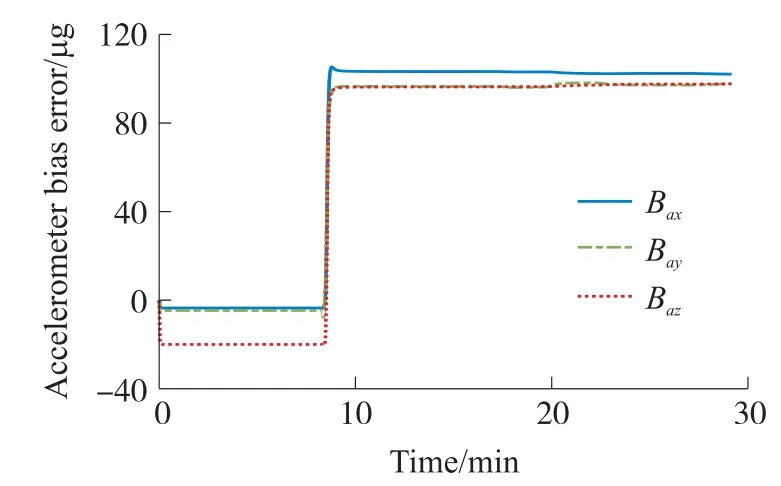
图5 加速度计零偏误差估计曲线
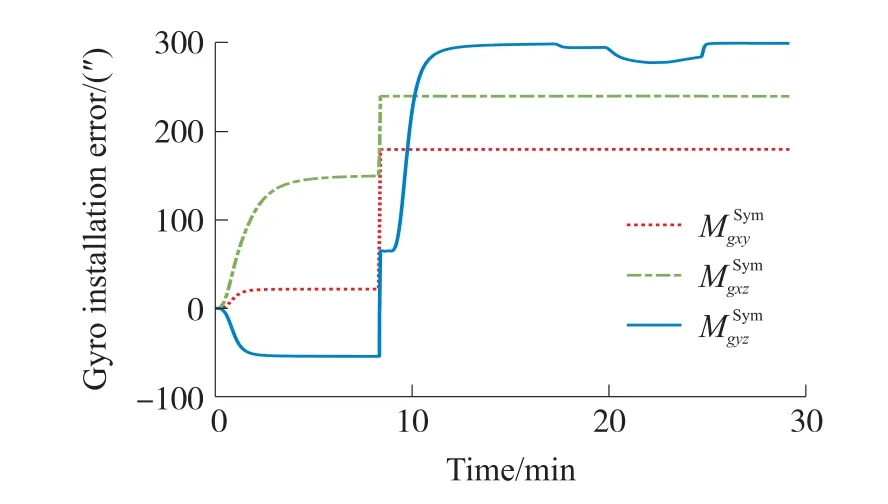
图10 陀螺安装误差估计曲线
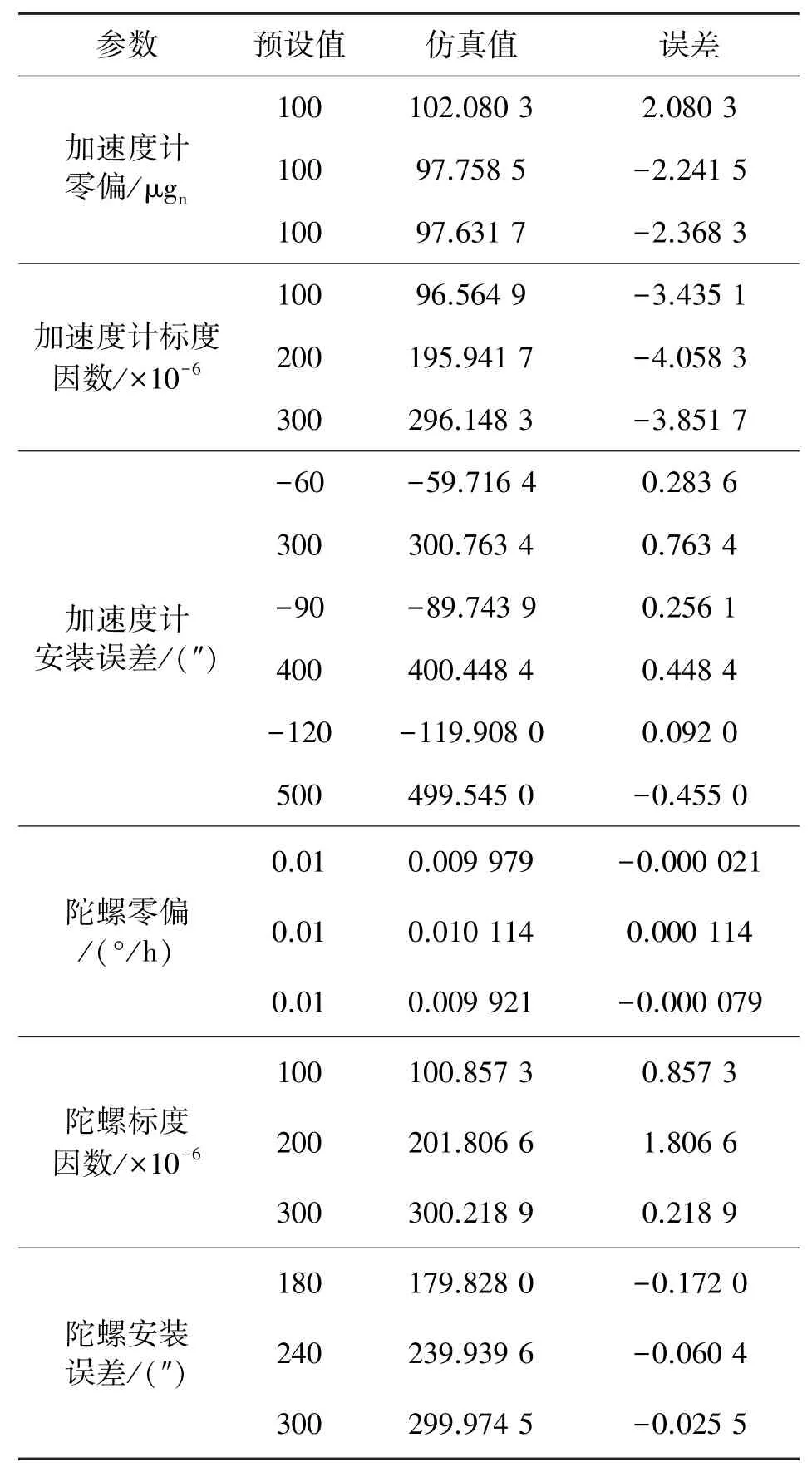
表1 标定误差估计结果
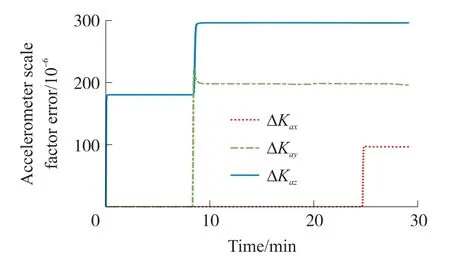
图6 加速度计标度因数误差滤波估计曲线
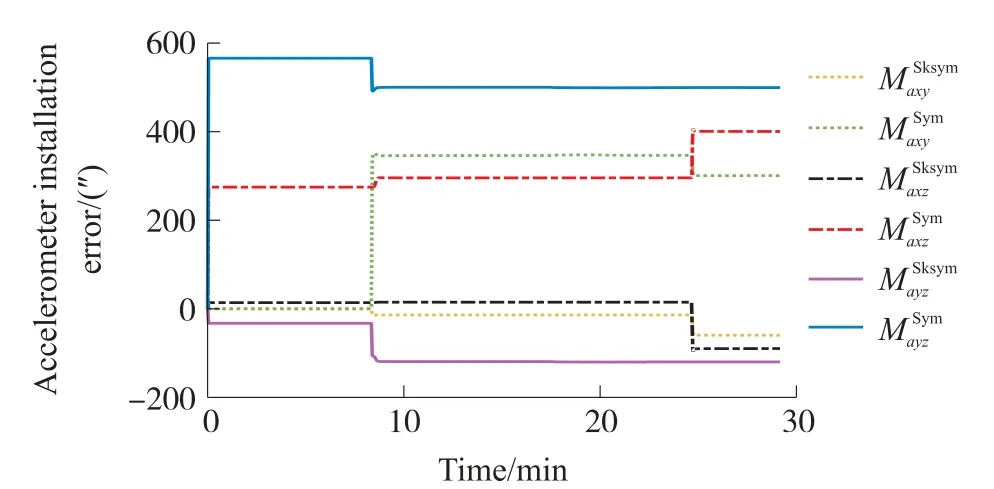
图7 加速度计安装误差估计曲线

图8 陀螺零偏误差估计曲线

图9 陀螺标度因数误差估计曲线
计算IMU待标定参数估计结果,陀螺零偏误差优于0.000 15°/h,加速度计的零偏误差优于3μgn,陀螺标度因数误差优于2×10-6,加速度计的标度因数误差优于4.5×10-6,安装误差角优于1″。
为验证基于矩阵分解的捷联惯导多位置系统级标定方法的可靠性,另设置3组不同的安装误差参数,分别为表1中安装误差参数预设值的40%、60%、80%(组1~组3),进行仿真对比实验。
表2以各组中加速度计和陀螺安装误差参数估计精度最低的误差项作为安装误差的估计误差,IMU各项安装误差标定精度均优于1″。

表2 对比实验安装误差估计误差
4 结论
本文基于矩阵分解原理对安装误差矩阵进行分解,将安装误差矩阵分解为对称矩阵和斜对称矩阵之和,对应地将安装误差角分解为不正交角和正交的失准角,建立了包含21项误差参数的标定误差模型。以导航速度误差和姿态误差为观测量,建立27维Kalman滤波模型。深入分析标定路径与误差参数辨识间的关系,根据陀螺和加速度计零偏可观测度的不同设置标定时间,设计了一种7位置标定编排方案,误差参数在标定结束后全部收敛,标定时间小于30 min。仿真实验验证了所提方法和标定路径的可行性。本文为系统级标定滤波法的路径编排提供了一些新思路,具有良好的工程参考价值。
