阵列式柔性力敏传感器的平衡校准标定方法*

王怀鹏周 旭姚志明杨先军*王 鹏秦嘉深

(1.安徽大学物质科学与信息技术研究院，安徽 合肥 230601；2.中国科学院合肥物质科学研究院，安徽 合肥 230031；3.中国科学技术大学研究生院科学岛分院，安徽 合肥 230031)

评价传感器的指标很多，如线性度、灵敏度、稳定度等[3]，其中线性度是支持传感器进行测量的一项基础指标，但由于传感器材质、工艺制作等方面的问题，对传感器的线性度有一定的影响，需要在使用前对传感器进行补偿及标定[4]。

国内外针对传感器的补偿及标定方法有很多，总的来说可以分为硬件补偿和软件标定两类。硬件方面，优化电路或制作工艺，通过芯片补偿传感器的输出电压，例如调节ADC的增益对电压进行补偿，从而优化传感器电路的输出反馈[5]。软件方面，通过设计上位机软件，优化曲线拟合的算法，对采集的压力数据进行补偿，减少传感器测量误差，例如基于二元插值算法的异频分步在线补偿方法，采用三次样条插值算法对传感器输出电压和工作温度插值，利用拉格朗日插值算法对压力和电压进行分段插值，减小非线性误差[6]；从信号处理的角度减少复杂噪声对压力传感器动态校准的影响[7]等等。但阵列式传感器有面积大、密度高的特点，通过传统的校准方法耗时耗力，且各点之间存在差异性，直接进行线性标定会降低传感器的输出表现。

本文提出了一种基于气压型一体化标定台的平衡校准标定方法，标定台通过密封空腔及硅胶膜传导达到均匀施加压力的目的，通过安全阀保障操作的安全性；平衡校准标定方法包括平衡和校准两部分，平衡部分利用Q值检验处理离群值，并对各个压力点的平衡值进行线性拟合，使得传感器阵列上的所有敏感点达到统一，校准部分使用LMBP-ANN模型，使得传感器输出达到期望水平。LMBP-ANN模型能高精度解决压力传感器中的重大误差问题，如增益变化和缺乏线性等[8]。

1 标定平台设计及数据采集

1.1 标定平台结构

本文使用气压型一体化标定台，成本低，量程大，受环境的影响小，误差小于±1%F.S，压力调节稳定。如图1所示，标定台主体由带有密封圈及抽拉垫板的壳体组成，外部气源通过气泵进入恒定气压阀，使得气源施加稳定，然后通过气压比例控制阀，使得气压可以连续成比例地进行调节，后进入腔体进行施压，同时限压阀始终将压力保持在安全范围内。腔体上方置有气压显示表用于显示当前腔内气压。

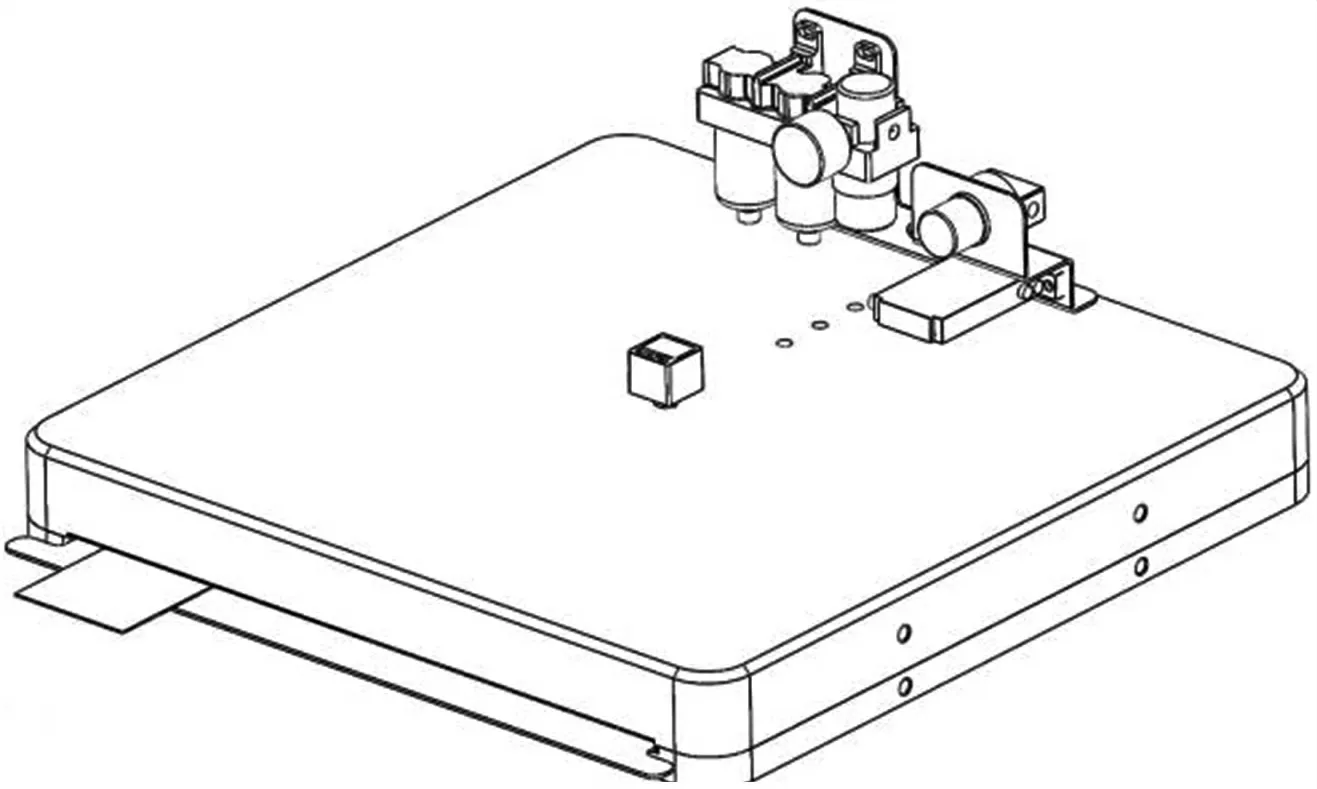
图1 标定台结构示意图

标定台上盖的下表面有向上呈正方体的凹槽，沿凹槽装有密封硅胶模，与抽拉垫板及底座成密封空腔，将传感器阵列固定在抽拉垫板上并推入腔内，气体进入腔内能够很好地通过硅胶模将压力均匀传导至待标定的传感器阵列上。

最后，石里克最大的问题是他对直观哲学提出的疑难亦可以反问于他自身：既然体验与认识有本质区别，那么概念的配列能保持事实的本来面貌吗？概念与对象的一义性判断之网如何能够达成？换句话说，既然体验与认识有本质区别，那么体验与认识又是如何能结合为一个具有统一性的系统呢？这一问题可以称为知识论中的超越问题。石里克大方地承认概念一义性的判断之网，并不能保证对事物的实在本质的知识，想获取事物的本质知识恰恰是直观哲学的错误。然而，直观哲学的本质论恰恰是以悬置事物的存在为前提，所以直观哲学绕开了实在本质的问题，而石里克却以事物的存在为事实，那么实在本质的问题就成为石里克认识论难以解决却如影随形的难题。

该装置在利用充气阀向腔体中加气时，能够通过气压表精准采集待标定传感器所受的实时气压，使得监测手段更加精准，从而保证了标定精度，安全气阀保证了标定操作过程的安全性，为大面积、平面式压力传感器的快速、安全、科学、自动精准标定提供了一种高效的方法。

1.2 数据采集

如图2所示，阵列式柔性力敏传感器由上下两层薄膜构成，其内表面分别印刷列导线和行导线，当两片薄膜叠合在一起的时候，行导线与列导线互相交叉，从而形成了一块具有若干个行和列交叉点所构成的点阵。阵列中每个点都是一个由特殊的压敏半导体材料构成的压力敏感点，当外力作用到敏感点上时，半导体的阻值会随外力的变化而成比例地变化，进而可以使用它来对大面积接触受力进行检测。

图2 阵列式柔性力敏传感器示意图

采集实验通过专门标定程序连接标定台进行，对传感器施加压力，逐渐提升至250 kPa，反复进行多次，具体流程如图3所示。

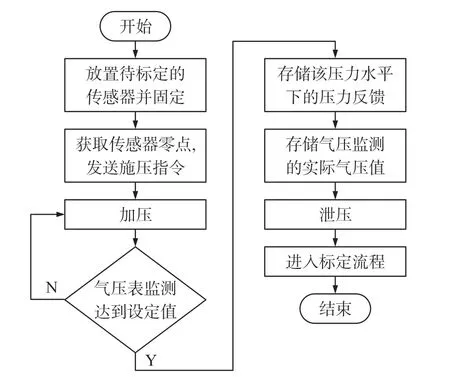
图3 数据采集流程图

从图4可以看出，传感器加压的整体线性度良好，对标定工作有很好的帮助，但从图5可以看出，各点的反馈曲线图存在差异，甚至存在个别的“坏点”需要处理或舍弃。图中的纵轴反馈AD值单位一般用最低有效位LSB(Least Significant Bit)表示，可忽略。

图4 传感器施压反馈值总和图

图5 传感器部分敏感点施压反馈图

2 问题分析

影响阵列式柔性力敏传感器反馈数值的因素很多，包括自身材质、温度、湿度、施压时间等等[9-12]，从而导致传感器出现温漂、时漂、滞后、物理非线性等误差。本文主要解决传感器的一致性及反馈值补偿问题，其他因素对本文所用传感器影响较小，暂不考虑，可在今后的工作中进一步解决。

2.1 一致性问题

①传感器表现不统一。由于材料、制作工艺等因素的影响，同一批次不同的阵列传感器或同一阵列传感器的各敏感点特性难以做到完全一致，存在一定的差异性，在相同的压力水平下不同的阵列传感器或同一阵列传感器的不同敏感点可能出现不同的反馈。

②传感器敏感点之间相互影响。阵列式传感器敏感点密集，每平方厘米可达6个点甚至更多，各敏感点压敏材料受外力发生形变电阻变化，不可避免地对邻近点产生影响，但在标定过程中，此偏差相对较小。

针对不同阵列传感器的一致性问题，可选择对每个阵列传感器进行标定并编号，绑定编号及标定结果；针对同一阵列传感器不同敏感点的一致性问题，需要使用平衡方法减少敏感点之间的差异性，优化传感器实际表现。

2.2 反馈值补偿问题

传感器的实际反馈值与施加压力值相差较大，缺乏对应关系的情况下无法直接使用。且传感器的反馈并非十分理想，如图6所示，阵列式柔性力敏传感器敏感点由特殊压敏材料制成，由于材料自身特性，其压力反馈存在一定的物理非线性。

图6 传感器单点线性度反馈图

在此情况下如何准确地得到输入输出的对应关系，从而对反馈值进行补偿，使反馈值与压力值统一尤为重要，处理该问题为校准工作的主要内容。

针对传感器反馈非线性的特性，如引用传统线性校准方法，需要根据反馈值特性分段进行校准，满量程情况下或需分3~5个部分，不同传感器分段情况也略有差异，校准起来相对复杂。本文主要引入LMBP-ANN模型进行全量程校准，无需分段，准确性也更高。

3 平衡校准标定方法

阵列式柔性力敏传感器由两层薄膜，横竖导线叠加构成，每个敏感点为特殊压敏材料。由于传感器敏感点数量大，间距小，且同一批次不同的传感器表现也略有差异，所以无法进行统一标定或单点标定。

为此，本文使用气压一体化标定台对阵列式柔性力敏传感器进行整体标定，标定分为平衡和校准两部分。

3.1 基于离群值处理的传感器平衡

阵列式传感器由若干压力敏感点构成，由于材质、制造工艺等的细微差别，各敏感点的反馈在未经平衡的情况下不可能做到完全一致，对传感器的实用性有一定的影响，因此需要对各个点进行平衡处理，使得在同一压力水平下，阵列式传感器各敏感点表现统一。

在进行平衡工作之前，需要对采集数据的离群值进行处理。在阵列式柔性力敏传感器中，可能会有个别点由于浆料、印刷等原因，存在反馈值与其他点差距过大的问题，这些差距很难通过校准工作纠正，如果不进行相应处理，而简单混入平衡过程，容易则对传感器的平衡精度产生影响。

对离群值的处理方法有很多，例如使用滤波或中值的方法减少误差[13]，用LOF算法剔除离群值等[14]。本文使用基于Q值检验的处理方法，在减少算法复杂度的基础上，能很好地适应柔性力敏传感器阵列的离群值处理。Q值检验又称为舍弃商法，它是通过对比整体内其他部分的份额来考察当前部分的不合理程度，从而判断是舍弃还是保留该部分[15]。将采集到的某一压力水平下的传感器压力反馈数据从小到大排序，并计算极差:

将最大及最小的各三位数n与其相邻值做差:

或

如果

则认为该点值为离群点，应当舍弃。每个压力下的平衡值为:

在多个压力水平下测算平衡值并进行线性拟合，最小二乘法的线性回归方程为:

所得结果即为平衡的结果。经过平衡过程，传感器阵列上的所有传感器元件表现统一，传感器标定的准确性和可信度有着很大的提高。

3.2 基于LMBP-ANN的传感器校准

阵列式柔性力敏传感器采集电路反馈的为AD值，而日常使用中需要的为实际压力值，校准的目的就是使得反馈的AD值与实际压力值相对应。阵列式传感器校准相对复杂，简单的线性函数不能很好地反馈其压力曲线。

常见的线性函数中二次函数和幂函数最贴近实验所得的压力变化曲线，但从图7、图8可以看出，二次函数和幂函数对70 kPa以下，加压逐渐稳定的部分拟合结果较差，从而导致表1中RMSE未达到理想范围，准确率有待提高。

图7 二次函数线性拟合图

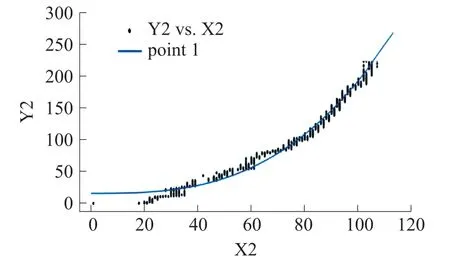
图8 幂函数线性拟合图

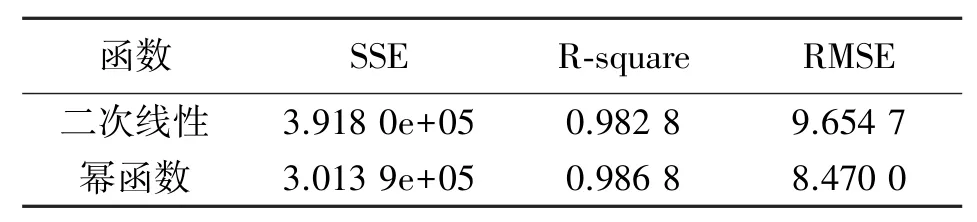
表1 线性函数拟合结果

因此，本文选用了LMBP-ANN模型，该模型对于解决传感器缺乏线性及滞后的问题有很好的帮助。LMBP用于最小化非线性函数的平方和，适合考评以均方差为指标的神经网络，符合阵列式传感器的标定要求。

通过试错的方法，从较少的神经元开始设计，逐渐增加隐藏神经元的数量，如表2所示，训练集、测试集、验证集分别取70%、15%、15%，最终表明隐藏神经元数量为12时效果最好。

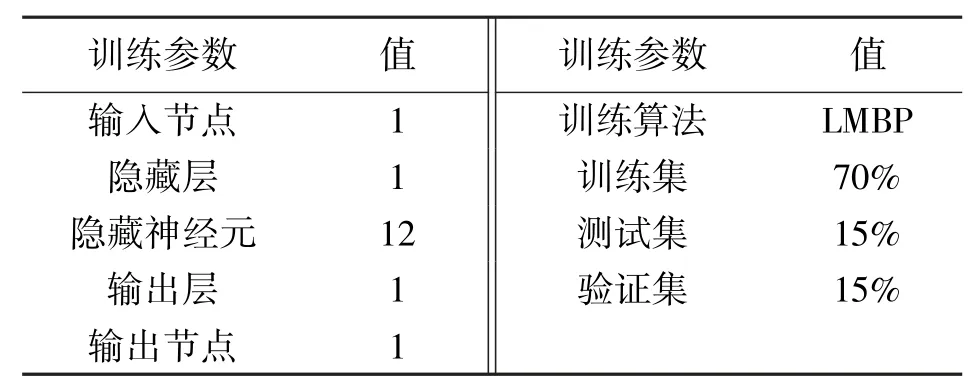
表2 模型参数

数据采集使用气压标定台，从0开始持续加压至250 kPa，每隔100 ms取一帧数据，每次训练约2 400组数据，部分传感器敏感点反馈AD值如图9所示。

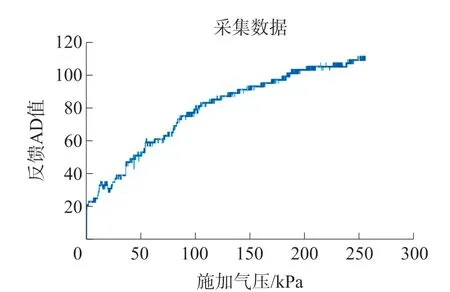
图9 部分传感器敏感点反馈AD值

如图10所示，训练集、测试集、验证集的MSE随训练次数增大而不断减小，直到6代训练也不减少，此时训练在146代达到最佳效果。

图10 EMS与训练周期

如图11、图12模型训练结果及误差直方图所示，该模型能够很好地实现对于阵列式传感器压力数据的自校准，训练集、验证集、测试集的R2均大于0.997，且91%的误差小于2.7%F.S，符合所需标准。

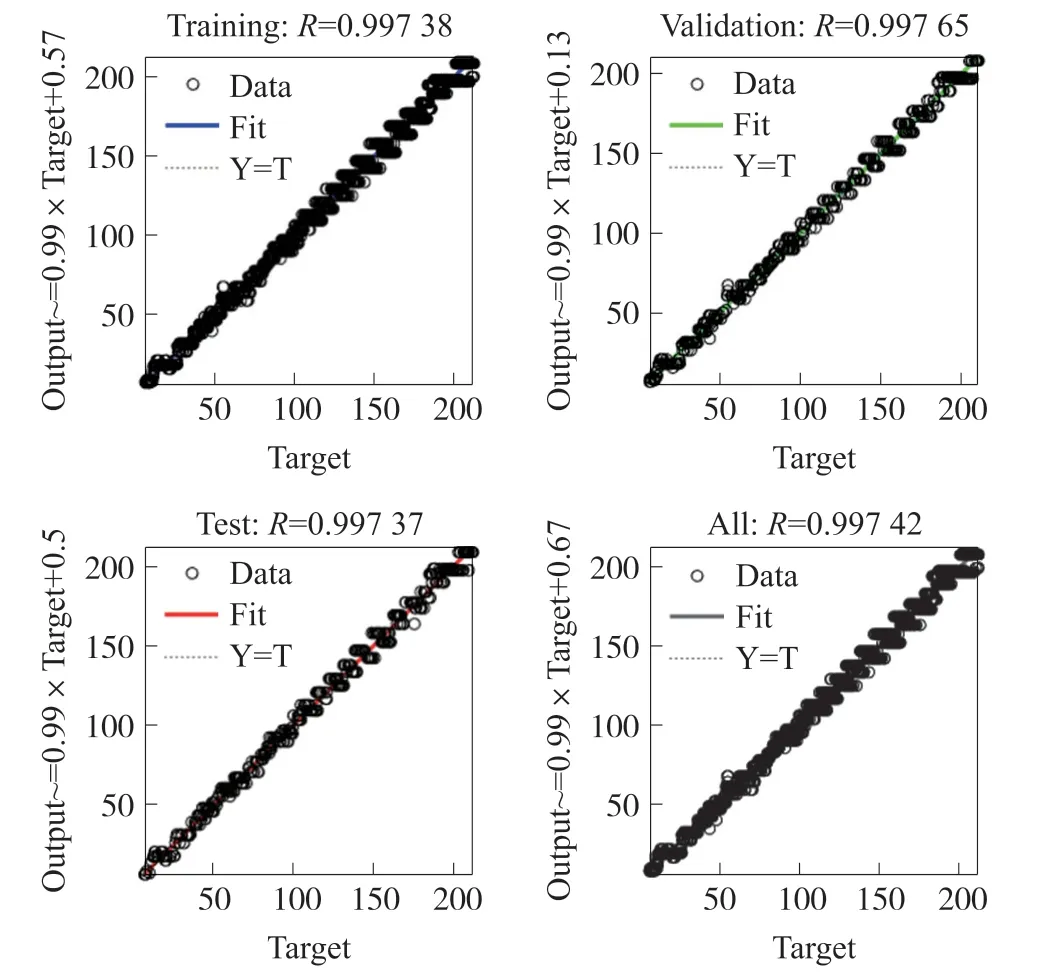
图11 LMBP-ANN模型训练结果

图12 训练误差直方图

如图13~图15训练结果所示，与贝叶斯正则化(Bayesian Regularization，BR)和标度共轭梯度(Scaled Conjugate Gradient，SCG)相比，LM也有更好的拟合表现和更小的误差。

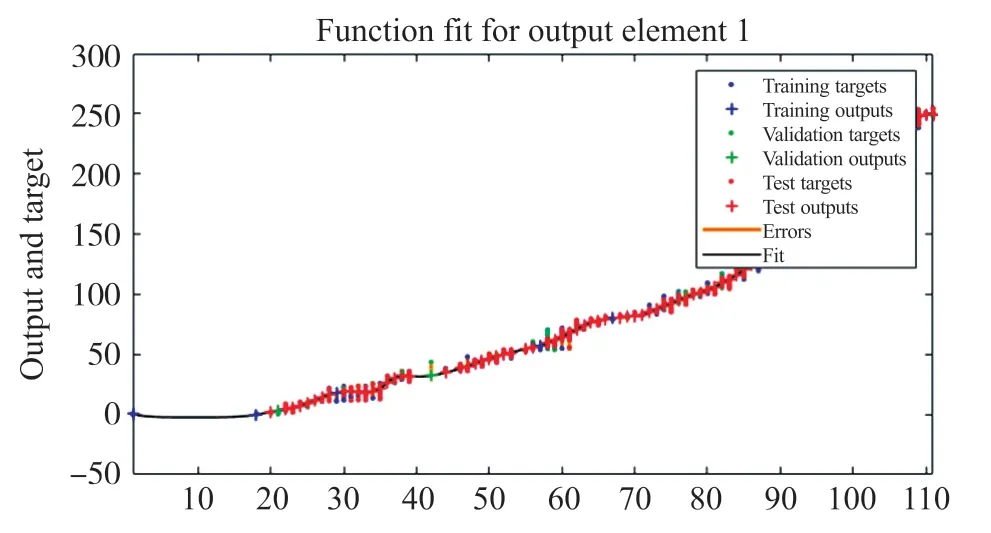
图13 LMBP训练结果图

图14 BR训练结果图

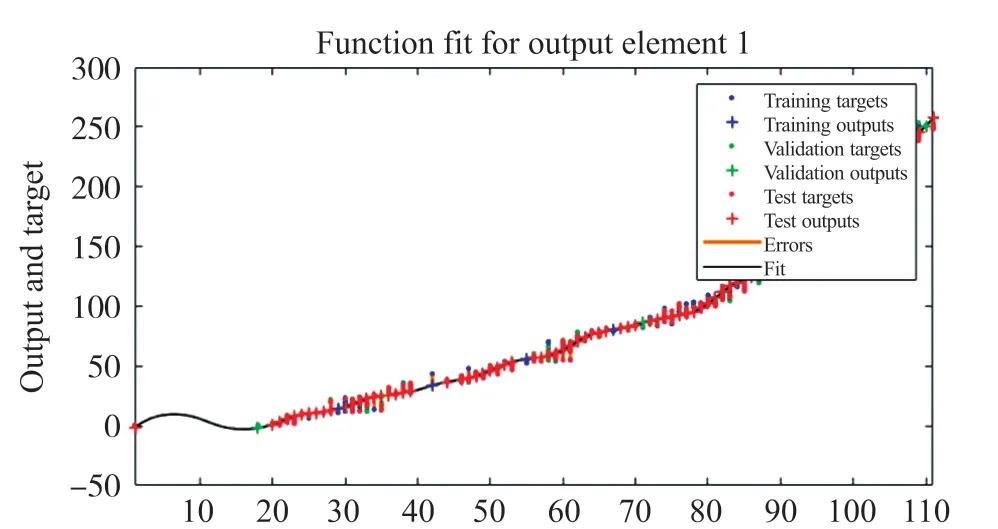
图15 SCG训练结果图

从表3可以看出，LMBP和BR的均方误差较小，优于SCG，但LMBP在小量程方面的拟合结果优于BR，故LMBP更适用于本文所用传感器。

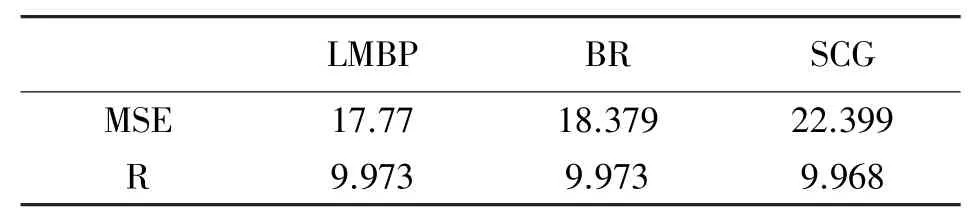
表3 模型误差比较

训练好的模型将保存至标定程序，并绑定传感器编号，以确定每一块阵列式柔性力敏传感器的压力补偿。

4 结论

本文简要介绍了阵列式柔性力敏传感器及相应标定装置，并提出了针对阵列式柔性力敏传感器进行整体快速标定的平衡校准标定方法，由平衡和校准两部分操作组成。平衡与校准两部分可以协同进行，也可以择一进行，平衡基于Q值检验法，处理离群值后通过平衡可以很好地保证整个传感器阵列反馈的统一，提高实用性；校准采用LMBP-ANN模型可以准确反馈施加的压力，R2大于0.997，精度为±4.7%F.S，且91%的误差小于2.7%F.S。标定方法性能优于传统方法，符合阵列式柔性力敏传感器在预期使用场景中的要求。