基于上限分析与随机响应面法的盾构隧道掌子面可靠度研究
2022-08-18陈海军张聚文孙志彬傅鹤林
陈海军,张聚文,孙志彬,傅鹤林
(1.中铁隧道勘察设计研究院有限公司,广东 广州 511458;2.合肥工业大学汽车与交通工程学院,安徽 合肥 230009;3.中南大学土木工程学院,湖南 长沙 410075)
0 引言
近年来,随着国内地铁修建里程的大幅增加,我国隧道工程得到了前所未有的发展,目前已成为隧道规模最大、数量最多、地质条件和结构形式最复杂的国家[1]。
传统的盾构隧道开挖面稳定性分析一般基于确定性的分析方法,即将土体围岩参数视为定值,通过建立合理的破坏面失稳模型求得其临界支护力或者开挖面的安全系数。乔金丽等[2]应用FLAC3D研究了考虑渗流效应的盾构隧道开挖面稳定性。黄阜等[3]将孔隙水压力做功作为一个外力功率引入上限定理的虚功率方程,得到了孔隙水压力作用下盾构隧道开挖面支护力的上限解。
隧道的地质条件受矿物成分、沉积历史、赋存环境等多种因素影响,其力学行为包含了众多的不确定性因素,特别是岩土体自身固有的力学强度不确定性和空间变异性使得隧道稳定性分析问题更加复杂[4]。传统的确定性分析方法只从性能指标方面对隧道稳定性进行评价,忽略了岩土参数的不确定性这一重要因素的影响,难以充分真实地评估隧道结构的工作状态,因而可靠度理论被逐渐引入到隧道工程中。Zeng等[5]对圆形隧道进行了可靠度分析,研究了隧道分布函数、隧道直径和支护压力对可靠性计算结果的影响。Li等[6]分析了分层土体中开挖隧道的掌子面可靠度问题,讨论了初始采样点个数、相关系数、分布类型及变异系数对失效概率的影响。
当隧道穿越富水地层或者穿越河流下方土层时,土体将受孔隙水压力作用,掌子面的稳定性与可靠度将大幅降低。康志军等[7]通过FLAC软件建立数值模型,研究了水位高度、渗流时间等因素对开挖面稳定性的影响。冯利坡等[8]结合水土压力统一计算理论,推导了二维对数螺旋破坏模式下的盾构隧道极限支护力,并将其拓展至多层土的情况中。现有文献对地下水作用下盾构隧道开挖面可靠度方面的研究较少,无法为实际工程的可靠度分析提供理论支持。
本文基于极限分析原理以及随机响应面理论,提出了考虑孔隙水压力作用下隧道开挖面的可靠度分析方法。采用基于空间离散技术的隧道开挖面破坏机构,提出了考虑孔隙水压力作用下的开挖面安全系数Fs上限解的求解流程。并考虑岩土参数黏聚力c以及内摩擦角φ的随机性,基于极限分析模型试验结果及拉丁超立方抽样方法,得到Hermite多项式,展开近似的隧道掌子面失稳功能函数的表达式。采用响应面法模拟量化研究了支护力、地下水位以及随机变量的变异性对隧道掌子面可靠度的影响,并通过工程实例研究了隧道掌子面可靠度的变化规律。
1 基于上限分析的确定性分析方法
确定隧道开挖面的稳定性一直是隧道施工的重点,极限分析上限法因其原理简单明确,计算过程方便,在隧道稳定性分析中常作为确定性分析方法被使用。极限分析从塑性力学的基本原理出发,通过构建机动速度场来研究开挖面的稳定性问题,利用上限分析求解结构的极限荷载,但结构在极限状态下发生破坏,一般选取最接近真实值的最小上限解作为极限荷载。
Davis等[9]首先提出将极限分析上限法应用于无黏性土隧道开挖面破坏机制与极限支护力大小的研究。Subrin等[10]假定掌子面破坏区域为对数螺线曲面,并利用上限法对维持掌子面稳定的最小支护力进行研究。国内学者吕玺琳等[11]通过与村山氏极限平衡法对比验证了极限分析法在求解极限支护压力的优越性。黄阜等[3]考虑地下水渗流的情况,基于空间离散技术建立了隧道开挖面上限破坏机制,并对掌子面开挖过程中安全系数上限解进行求解。由于利用离散技术构建的开挖面破坏机制与模型试验得到的开挖面破坏模式十分吻合,在学术界得到广泛的认可,故本文采用黄阜等[3]提出的上限机构作为本文可靠性分析的确定性模型。
1.1 孔隙水压力作用下的上限定理
Viratjandr等[12]将孔隙水压力视为一个外力作用在土体颗粒上,则孔隙水压力做的功等于孔隙水压力使土体颗粒膨胀做的功和孔隙水压力在速度场边界上做的功之和。孔隙水压力作用下的极限分析上限定理可以用下式表示:
(1)

u=ruγz。
(2)
式中:γ为土体重度;z为地表到计算点的垂直距离;ru为孔隙水压力系数,可以采用三轴试验测得其数值[13]。
1.2 基于空间离散技术的隧道开挖面破坏机制
基于Mollon等[14]提出的离散思想,本文采用黄阜等[15]构建的适用于孔隙水压力作用下的盾构隧道开挖面二维破坏机制作为确定性分析模型。假设刚性塌落体ABE绕旋转中心O以角速度ω旋转,其他参数的物理意义如图1所示。

AB为隧道的开挖面;O′为AB中点;D为隧道直径;C为上覆土层的厚度;Hw为地下水位线;速度间断面AE、BE分别交隧道掌子面于A、B点。
开挖面塌落体ABE由速度间断面AE和BE构成,现以速度间断面BE为例来说明整个塌落体ABE的生成过程。令Bi为BE上任意一点,直线j为旋转中心O与Bi点的径向连线,并记j与起始方向的夹角为θi,如图2所示。假设OBi绕旋转中心转动1个角度δθ后得到另一条径向直线j+1。根据相关流动法则,速度间断面上每一点的速度矢量vi与速度间断面的夹角等于摩擦角φ。故只要将点Bi处的速度方向偏转1个角度φ,并延长至与径向直线j+1相交,其交点即为下一个离散点Bi+1,按照此方法不断循环就可以得到速度间断面BE。采取同样的方法从A点开始则可以生成速度间断面AE,当上下两间断面相交于点E时,整个塌落体ABE生成完成。

图2 基于空间离散技术的开挖面破坏机制
在本文所考虑情况中假设机构不露出地表,故E点纵坐标YE应位于地表之下,即
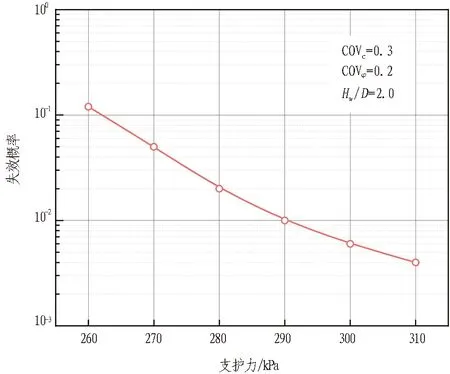
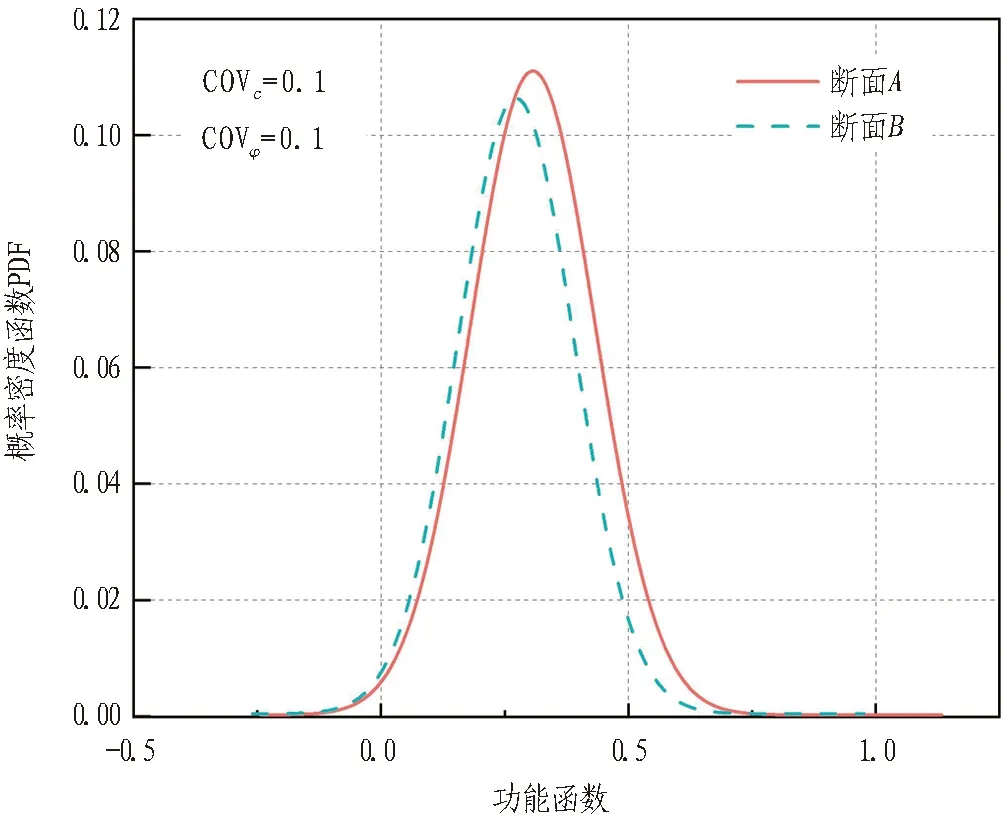
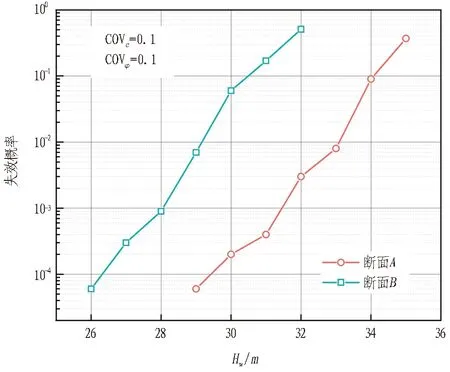
YE (3) 同时旋转中心O应位于隧道上方,故O点纵坐标Yo应位于隧道上方,即 Yo>D。 (4) 由于机构的离散性,在计算重力功率时,整个机构的重力功率可由每个单元重力功率之和得到。在计算过程中,整个塌落体的重力功率计算可分为2部分进行,最后相加得到,计算示意图如图3所示。 (a) 如图3(a)所示,每一个单元为三角形,先分别计算每个单元三角形ABiBi+1的重力功率,然后累加就得到Ⅰ部分的重力功率为 (5) 式中:γ为土体重度;Si为三角形ABiBi+1的面积;RGi为旋转中心O到三角形重心Gi的距离;θGi为OGi与初始方向的夹角。 如图3(b)所示Ⅱ部分的重力功率采用叠加法得到,即单元AiBiBi+1Ai+1的重力功率由单元OBiBi+1与单元OAiAi+1的重力功率之差表示: (6) 式中:SAi、SBi分别为三角形OAiAi+1、OBiBi+1的面积;RAi、RBi分别为O到三角形OAiAi+1、OBiBi+1重心的距离;θGAi、θGBi分别为直线OGAi、直线OGBi与初始方向的夹角。 故整个破坏机构的重力功率 Wγ=W1+W2。 (7) 支护力σ作用在开挖面上,将其视作均布荷载,其功率可由下式计算: (8) 式中:rB为旋转中心O到掌子面下边界B点的距离;θA与θB分别为直线OA、OB与初始方向的夹角,其他符号意义同上。 由于假设塌落体为刚体,内能耗散只发生在速度间断面上,并且通过离散技术生成的速度间断面是由若干段直线构成的,所以速度间断面上总的内能耗散功率可以通过将每一段直线上的内能耗散功率进行叠加得到。按此方法可得速度间断面上的内能耗散计算式为: (9) (10) D=DBE+DAE。 (11) 式(9)—(11)中:c为黏聚力;φ为摩擦角;lBi、lAi分别为BiBi+1、AiAi+1的长度;RAi、RBi分别为点O到AiAi+1、BiBi+1中点的距离。 孔隙水压力功率可由式(12)计算[12]。 (12) 式中各个参量含义与上文一致。由于假设塌落体ABE为刚体,故体应变为0,即式中的前一项为0,孔隙水压力功率全部在速度间断面和开挖面上产生。 安全系数Fs可以表示为 Fs=minf(θA,θB|c,φ,γ,C,D,Hw,ru)。 Fs求解需结合二分法与强度折减法进行,整个流程简述如下: 1)给定安全系数上限值F1、下限值F2,得到折减系数 Ft=(F1+F2)/2。 (13) 2)对各土体参数进行折减 (14) (15) 3)求解折减后重力功率Wλ、支护力功率Pf、孔隙水压力功率Wu及内能耗散功率D。 4)以内外能耗的差值作为判别标准,当D>Wγ+Pf+Wu时,表示在变量的可行域中未找到临界状态下的边坡,则将Ft赋给上限值F1,反之将Ft赋给下限值F2;循环2)—4),直至|F1-F2|<εF,此时的隧道掌子面安全系数为 Fs=Ft。 (16) εF为安全系数的计算精度,一般可取0.01。 由于隧道机构与其赋存环境的复杂性,隧道掌子面的功能函数往往具有高阶非线性的特征,难以直接求得明确解析表达式,而响应面法却可以利用较简单的显式功能函数对真实复杂失效面进行拟合,具有快捷准确的特点,在隧道可靠度分析领域得到越来越广泛的应用。 随机响应面法最早由Isukapalli提出[16],具有正交特性且收敛性好的特点,能够较准确地模拟整个样本空间内结构输出响应量的变化过程。随机响应面法分析的第1步是将输入随机变量X表示为标准正态分布随机变量U的函数,对于正态分布的随机变量X来说,它和标准正态分布随机变量之间的映射关系[16]如下: X=μx+σxU。 (17) 式中μx、σx分别为X的均值与标准差。 输入随机变量的个数根据所求问题的需要确定,但一般为了减少计算量,通常选择最敏感的随机变量作为输入随机变量。 输出响应量的展开形式与随机变量分布函数相关,本文假设随机变量(c,φ)呈正态分布,采用Hermite多项式展开来建立输出响应量与输入参数间的显式函数关系。输出响应量Y的Hermite随机多项式展开表示如下[17]: (18) 式中:a0,ai1,ai1i2,ai1i2i3,ai1i2i3···in均为待定系数;n为标准正态随机变量的个数;Γn(Ui1,Ui2,Ui3,…,Uin)为n阶Hermite多项式,关于Hermite随机多项式展开及其拟合隐式函数理论可详细参考文献[18-19]。 本文采用3阶Hermite随机多项式展开来拟合响应面功能函数,随机变量为c与φ,其具体表示如下: Z(c,φ)=a1+a2c+a3φ+a4c2+a5φ2+a6c3+ a7φ3+a8cφ+a9cφ2+a10c2φ。 (19) 式中a1,a2,···,a10均为系数。 盾构隧道掌子面失效的功能函数定义为: Z(c,φ)=Fs-1。 (20) 设计响应面需要进行配点,合理的配点选取是确定待定系数的关键,往往决定着响应面法的计算效率和计算精度。拉丁超立方抽样是一种全空间填充且非重叠的多维分层抽样方法,全空间填充抽样确保了即使在没有详细的源函数特性的情况下,也可以得到该函数在整个设计空间的信息,非重叠抽样则确保没有重复和多余的数据点,因而在可靠性分析中得到广泛的应用。 本文将极限分析原理和随机响应面理论进行耦合,构建出考虑孔隙水压力下隧道开挖面稳定性的可靠度分析方法。具体流程如下: 1)通过拉丁超立方抽样方法抽取多组配点(c,φ),并通过上限法求解对应的隧道掌子面安全系数。 2)通过Hermite多项式来拟合隧道掌子面失稳功能函数的表达式。 3)随机抽取对应c、φ(c=10 kPa、φ=20°;COVc=0.2、COVφ=0.1)工况下的大量配点,通过功能函数求解安全系数,并与上限法结果进行比较,验证功能函数的正确性。得到的误差曲线如图4所示。结果表明,图4中所有点的误差都在5%之内。这说明,所求失稳功能函数满足计算精度要求,可用于可靠度分析。 图4 功能函数与上限法结果对比 4)最后直接利用蒙特卡罗进行50 000次模拟,评估隧道的失效概率。 本节通过对隧道掌子面进行可靠度分析,对随机变量变异性、地下水位高度及支护力大小对隧道掌子面可靠性的影响进行了研究。计算过程中确定性参数的取值如下:土体容重γ=20 kN/m3,隧道直径D=10 m,地下水位Hw=2D,隧道埋深C=20 m,孔隙水压力系数ru=0.2。隧道支护压力取1.1倍极限支护力σc,根据已有文献[20],本文假设岩土材料参数的概率分布服从正态分布,随机变量及分布参数如表1所示。 表1 随机变量及分布参数 通过拉丁超立方方法抽样抽取20组配点(c,φ),并采用上限法求解对应的隧道掌子面安全系数,用以拟合Hermite多项式近似的临界状态曲面,结合蒙特卡罗法进行50 000次模拟,求得结构失效概率约为0.1%。根据可靠度分析结果绘制功能函数概率密度函数(PDF)及累计分布函数(CDF),结果如图5所示。由图5 PDF曲线显示功能函数近似服从正态分布;从CDF曲线中可知功能函数值<0的统计量约占0.001,即隧道掌子面失效概率约为0.1%。 (a)COVφ=0.1 为进一步分析随机变量变异系数对隧道掌子面可靠度的影响,控制单一变量COVc与COVφ,得到失效概率与变异系数关系图,如图6所示。图6(a)中COVc=0.2,COVφ=0.1;图6(b)中COVc=0.3,COVφ=0.2。整体上看,失效概率随变异系数的增大而增大。图6(a)中,变异系数对失效概率的影响呈非线性特征,当变异系数较小时,隧道掌子面的失效概率增长较慢,随着变异系数的增大,其对失效概率的影响愈发显著,失效概率的增长速度不断增大。 为更好地展现黏聚力变异系数的影响,取较高水平COVc与COVφ重复上述模拟,结果如图6(b)所示。具体来说,当COVc从0.1增加至0.5时,其失效概率由2%仅增加至8%左右,但整体维持在一个较高水平;当COVφ从0.1增加至0.3时,失效概率由5×10-3增加至1×10-1左右。对比2条曲线可以发现COVφ对失效概率的影响比COVc更加敏感,且当COVφ维持在较高水平时,COVc对失效概率的影响并不显著,而当COVc维持在较高水平时COVφ对失效概率的影响依然显著,故内摩擦角φ的变异性的确定对获得可靠的概率结果是尤为重要的。 同时,为丰富变异系数对失效概率影响的探讨,补充1组不同c、φ取值下(c=20 kPa、φ=15°;COVc=0.3、COVφ=0.2)的对照组,具体结果如图6(c)所示。从图中可以看出,变异系数对失效概率的影响与前述结果相符合,但失效概率整体维持在较高水平。 (a) 地下水位的变化会改变围岩内部孔隙水压力的分布,进而影响隧道掌子面的失效概率。图7绘制了失效概率随水位高度与洞径比值Hw/D变化的曲线图,可以分析地下水位对隧道开挖面可靠度的影响。 图7 不同地下水位Hw/D对失效概率的影响 从图中可以看出,在对数坐标上失效概率随Hw/D增加基本呈线性增长,掌子面破坏概率受地下水位的影响显著。当地下水位Hw/D从1.4增大到2.2时,失效概率从约3×10-3增大到0.2,增大近2个数量级,且随水位Hw/D增大,其对失效概率的影响愈发显著,当Hw/D从2.1仅增大到2.2时,失效概率就增大了近0.1。由此可见,地下水作用对盾构隧道掌子面稳定性的影响是不可忽视的,故在盾构隧道的设计与施工过程中,当盾构隧道需要在地下水含量丰富的地层中掘进时,应特别注意孔隙水对掌子面稳定性的影响,根据需要采取适当的加固措施以保证工程建设的顺利完成。 分析支护力对隧道掌子面可靠度的影响,可以为判断开挖面在现有支护力作用下是否能维持稳定提供有效参考。 在维持其他参数不变的情况下,绘制了失效概率与掌子面支护力的关系图,如图8所示。从图中可以看出,支护力与失效概率的对数坐标近似呈线性关系,随着支护力的增加失效概率减小,且这种减小趋势随着支护力的增大而有所放缓。Yang等[20]通过引入容许失效概率的概念,根据失效概率与支护力关系图可得到盾构隧道开挖面安全的支护力范围,不同的容许失效概率对应于不同的支护力范围。例如:容许的失效概率取0.01时,则相对应的支护力范围应为σ≥290 kPa。 图8 支护力对失效概率的影响 长沙市湘江隧道工程位于橘子洲大桥和银盆岭大桥之间,场区地质构造以断裂构造为主。湘江隧道分别下穿傅家洲、橘子洲和湘江东岸3条断层破碎带,且距离隧道顶部极近的圆砾层又具有含水量、高透水性好的特点,致使该段隧道在施工时易出现涌水、坍塌等问题。因此,本节选取湘江隧道作为分析对象,验证本文提出的方法在实际应用中的可行性。 湘江隧道构造分为南北两线,故在南北两线各取1个典型断面(分别记为断面A与B,断面里程为SK1+355与NK0+788)进行可靠度分析,断面示意图如图9所示。计算过程中确定性参数的取值如下:土体容重γ=23.9 kN/m3,隧道洞径D=11.3 m,埋深分别为CA=13.4 m、CB=9.2 m,地下水位取高水位HwA=31.9 m,HwB=28.8 m,孔隙水压力系数ru=0.2。按极限分析法得到的2个断面的极限支护力约为193 kPa与175 kPa,为确保工程安全,在分析过程中断面A、B上的支护力取1.1倍的极限分析值。其余随机变量及分布参数如表2所示。 (a) 表2 随机变量及分布参数 图10示出了湘江隧道A、B断面的功能函数的概率密度曲线与累计分布曲线。从图中可以看出功能函数都近似服从正态分布,2个断面的PDF与CDF曲线具有极好的一致性,且失效概率均不到1%,具有较高的可靠度。 (a)概率密度曲线 对地下水位高度及支护力对掌子面可靠度的影响进行探讨,绘制了失效概率随单一参数变化的曲线图,如图11和图12所示。从图11中可以看出随Hw的增大隧道掌子面失效概率增大,且随水位Hw的升高,其对失效概率的影响越来越大,尤其在水位较高时,水位Hw的较低增幅都会导致失效概率的激增,说明地下水作用对盾构隧道开挖面的稳定性影响是比较显著的。同时,对比A、B断面的影响曲线可以发现,水位相同时断面A的失效概率远小于断面B,失效概率相差超1个数量级,在实际开挖过程中对开挖面的稳定性需充分研究,不可一概而论。 图11 湘江隧道地下水位对失效概率的影响 图12反映失效概率与支护力在对数坐标上近似呈线性关系,随着支护力的提高,失效概率有明显的下降,支护力在增加20%左右时,掌子面失效概率减小100倍左右,且在支护力取值大于215 kPa(断面A)与195 kPa(断面B)时掌子面的失效概率就可降至10-3以下。本文仅考虑坍塌破坏情况支护力取值不可过大(否则会导致隆起破坏),实际工程中可以通过适当提高支护力降低结构失效概率。 图12 湘江隧道支护力对失效概率的影响 从上述分析结果可知,采用本文方法计算所得地下水位与支护力对失效概率的影响与湘江隧道掌子面稳定性变化趋势较为吻合。此外,功能函数计算得到的失效概率不到1%,说明在湘江隧道施工过程中有效维持了开挖面的稳定性,而实际工程中隧道的顺利完工也印证了这一结论。由此可见,本文计算得到的隧道开挖面失效概率是可靠的,可以用于实际工程中孔隙水压力作用下隧道开挖面的稳定性分析。 为了进一步验证本文方法的有效性,将本文结果与传统土压平衡盾构法方法对比,土压平衡盾构法确定支护力公式如下: σc=σ水平侧向力+σ水平水压力=q1γh1+q2γwh2; (21) h1=0.45×2s-1ω。 (22) 式(21)—(22)中:对应于湘江隧道所处Ⅴ级围岩q1可取0.35;γ为土体重度;h1为隧道中心点的深度;对应风化岩层q2可取0.4;γw为水的容重;h2为地下水位距刀盘顶部的高度;s为围岩级别;ω为宽度影响系数,ω=1+i(B-5),B为坑道宽度,当B<5 m时,取i=0.2,当B>5 m时,取i=0.1。 按传统方法计算得断面A、B的极限支护力约为180、168 kPa,相比于极限分析结果(193、175 kPa),二者相对误差分别为7%与4%,都在可接受范围内,表明本文方法是有效的。在实际施工过程中,尤其是当隧道下穿地质不良区域时,支护力不足可能导致开挖面失稳概率陡增,在工程中合理的支护力评估与选取是必要的。在湘江隧道现场施工过程就采用了本文方法确定支护力,并取得了良好效果。此外,相比于传统的确定性分析,本文采用的概率方法能更合理地描述岩土工程中存在的固有不确定性及模糊性的影响,在实际隧道施工中更具指导意义。 本文采用基于空间离散技术的隧道开挖面破坏机制,考虑孔隙水压力作用对隧道开挖面稳定的影响,在假设土体黏聚力与内摩擦角正态分布的条件下,应用基于Hermite多项式展开的随机响应面法,提出了隧道掌子面的可靠度方法(仅考虑隧道失稳坍塌破坏)。该方法不需要进行大量的蒙特卡洛抽样与模拟,可以准确有效地计算隧道掌子面的失效概率,在保证计算精度的同时又具有较高计算效率。主要结论如下: 1)代表土体参数随机性的变异系数对隧道的可靠度有较大影响,随着变异系数的增大,掌子面失效概率呈非线性增大,且可以发现COVφ对失效概率的影响比COVc更敏感。为了保证隧道工程结构安全性且获得更为经济合理的支护方案,建议在隧道结构设计中充分考虑土体参数的随机性影响。 2)地下水作用对隧道开挖面可靠性影响显著,随着地下水位的升高,掌子面失效概率在对数坐标上呈近似线性且显著的增长。当隧道需要在地下水含量丰富的地层中掘进时,及时进行监控量测,以防止掌子面发生涌水突泥及坍塌事故。 3)作用于掌子面上的支护力对隧道稳定性的提升有较大的增益。实例分析中掌子面支护力增加20%左右时,掌子面失效概率减小100倍左右。工程中可以通过选择合适的支护力将失效概率控制在可接受的范围内。 4)工程实例的分析表明,本文提出的概率方法可以有效给出实际隧道施工时的掌子面失效概率,可以更好的指导现场施工。但本文对隧道内孔隙水分布进行了简化,为得到更加准确的可靠度结果,可以采用更加切合实际的孔隙水分布模型。1.3 孔隙水压力作用下破坏机制的能耗计算

2 随机响应面法基本原理
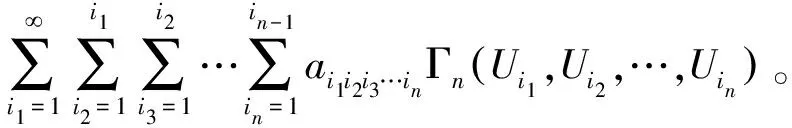
3 盾构隧道掌子面的可靠度分析方法

4 掌子面失效概率的参数分析


4.1 变异系数对可靠度的影响

4.2 地下水位对可靠度的影响

4.3 支护力对可靠度的影响
5 工程实例分析
5.1 隧道断面的影响


5.2 地下水位高度及支护力的影响

6 结论与讨论
