基于均值-CVaR的灾后临时献血点选址分布式鲁棒优化方案研究

张 玲 李锦棚 高妙仙

(1. 福州大学经济与管理学院， 福建福州 350108；2. 福州大学数字中国研究院， 福建福州 350108)

一、引言

地震灾害问题一直在世界范围内受到关注，由于地震发生的频率以及损害程度无法准确估计，一旦发生严重地震灾害时通常波及范围大，影响时间长。在地震发生之后，政府或应急管理部门需要快速启动救援系统，保障灾民的生命财产安全，同时需要向这些受到灾害侵袭的地区和人员运送充足的物资来应对危机。而在众多救援物资中，血液资源是一种稀缺但对人体生命健康非常重要的医疗物资。在地震发生后，大量伤员的输血治疗会导致短期内血液需求量剧增，给受灾地的应急血液保障带来严峻挑战。但是血液的来源非常有限，对血液制品需求只能通过日常存储的血液以及灾后临时收集的血液来满足。因此，优化灾后的血液供应网络，使其既能够有效保障伤员的生命健康，又能平衡好社会成本，对应急管理工作具有重要的现实意义。

在实际救援情况中，受救援环境的复杂性以及需求的随机性等现实因素的影响，物资分配与实际需求不匹配、物资短缺或高度冗余、救援效率差等现象很容易发生。为了处理这种不确定性，一些学者研究了不同的决策方法，包括随机优化和鲁棒优化。随机优化理论假设不确定变量服从某一特定的分布情况，求得期望值最优的结果，例如Ensafian等(1)Ensafian H.,Yaghoubi S.,Modarres Yazdi M.,“Raising quality and safety of platelet transfusion servicesin a patient-based integrated supply chain under uncertainty”，Computers & Chemical Engineering,vol.106(2017),pp.355-372.、Gunpinar等(2)Gunpinar S., Centeno G.,“Stochastic integer programming models for reducing wastages and shortages of blood products at hospitals”,Computers & Operations Research, vol.54(2015),pp.129-141.、Ghatreh Samani等(3)Ghatreh Samani M.R.,Torabi S.A., Hosseini-Motlagh S-M.,“Integrated blood supply chain planning for disaster relief”,International Journal of Disaster Risk Reduction, vol.27(2018),pp.168-188.分别假设不确定变量服从泊松、伽马和均匀分布，研究血液的库存问题。传统鲁棒优化则不考虑不确定变量的分布情况、旨在找到最坏情况下最优的结果，例如董海等使用鲁棒优化方法找到不确定变量最坏情况下使总成本以及血液储存量最小的结果。(4)董海、吴瑶、齐新娜：《基于改进差分鲸鱼优化算法的血液供应链网络多目标鲁棒优化设计》，《计算机应用》2021年第8期。周愉峰等从国家层面的血液战略储备角度思考，运用鲁棒优化的思想，以血液保障及时度最高为目标，建立国家血液战略储备库选址-库存模型。(5)周愉峰、李志、刘思峰：《基于随机p-鲁棒优化的国家血液战略储备库选址-库存模型》，《中国管理科学》2018年第10期。然而，随机优化对于不确定变量分布的选择具有主观性，并没有考虑到不确定变量分布情况也具有随机性，而鲁棒优化对于不确定变量的处理完全不考虑随机性。分布式鲁棒优化则结合随机优化与鲁棒优化的特点，旨在找出最坏分布情况下最优的方案。Wang等研究了在只有少量历史观测数据的情况下采用分布式鲁棒优化灾害后的血液供应网络，对血液库存预部署和救援活动提供指导。(6)Wang C., Chen S.,“A distributionally robust optimization for blood supply network considering disasters”,Transportation Research Part E: Logistics and Transportation Review, vol.134(2020).Qiu等考虑在需求不确定性和供应中断的情况下，通过对一些设施故障或连接线路中断引起的供应中断场景概率进行描述，采用分布式鲁棒优化进行求解。(7)Qiu R.,Wang Y.,“Supply Chain Network Design under Demand Uncertainty and Supply Disruptions: A Distributionally Robust Optimization Approach”,Scientific Programming, vol.106 (2016),pp.1-15.然而不管是随机优化还是分布式鲁棒优化均为风险中性决策(即仅考虑期望值，传统鲁棒优化则是极度厌恶风险决策)，没有考虑决策者的风险偏好，并不适用于现实情况，决策者的风险偏好会对决策行为产生重大影响，因此需要把决策者的风险规避特征引入到血液供应网络的研究中。

对于选择怎样的风险度量方法来有效地度量决策者的风险规避特征，目前广泛使用的是风险价值方法(VaR)，该方法最初由Philippe提出，被广泛运用于金融投资领域。(8)Philippe Jorion ,Value at Risk:The Benchmark for Controlling Market Risk,New York: McGraw-Hill,2000.但由于VaR方法无法预测临近的不利事件并且计算困难，在此基础上Rockafellar提出了条件风险价值方法(CVaR)，它可以有效降低概率事件对决策方案的影响，弥补了VaR不满足次可加性、未考虑尾部风险等缺陷。(9)Rockafellar R.T.,Uryasev S.,“Conditional value-at-risk for general loss distributions”,Journal of banking & finance,vol.26(2002),pp.1443-1471.简惠云等使用CVaR工具分析了具有风险偏好零售商的条件风险值及最优订货决策。(10)简惠云、许民利：《基于CVaR的供应链契约及其实验研究》，《管理科学学报》2015年第10期。黄金波等使用CVaR工具构建风险优化模型和风险对冲模型，实现风险的估计与风险的管理同步进行。(11)黄金波、李仲飞、姚海祥：《基于CVaR核估计量的风险管理》，《管理科学学报》2014年第3期。然而，Wan等发现CVaR方法仅考虑了低于分位数的平均收益值，忽略了高于分位数的部分，这使得决策者的决策目标偏低，整体预期利润也有所下降。(12)Wan Y.,Clutter M.L.,Mei B.,et al.,”Assessing the role of U. S. timberland assets in a mixed portfolio under the mean conditional value at risk framework”,European Journal of Operational Research,vol.50(2015),pp.118-126.为了改进CVaR方法的缺陷，陈宇科等采用均值-CVaR方法分析了闭环供应链成员在分散决策和联合决策时的最优决策，验证了均值-CVaR比CVaR更能提高零售商的订货量和利润。(13)陈宇科、熊龙、董景荣：《基于均值-CVaR 的闭环供应链协调机制》，《中国管理科学》2017年第2期。尚春燕等使用均值-CVaR方法研究制造商创新情形下回购契约供应链的订货及协调机制，通过比较也证明了均值-CVaR方法的优势之处。(14)尚春燕、关志民、米力阳：《基于均值-CVaR 的回购契约供应链创新协调机制》，《工业工程》2019年第5期。然而上述文献都是通过对风险的度量研究金融投资领域或者传统供应链协调领域，缺乏对应急管理领域的应用研究。

综上所述，以往的文献对于如何将风险度量方法引入应急血液供应网络的研究较少。因此本文将采用“均值-CVaR”方法来度量风险规避的应急决策者，使用分布式鲁棒优化方法优化灾后临时献血点选址决策。本文的主要贡献如下：

(1)对应急物资中的细分领域——血液资源进行研究，拓展了我国应对突发灾害事件物资储备领域的研究类型；

(2)应急决策者可以根据自身规避风险的程度，利用模型进行决策；

(3)所提出的应急血液供应网络配置决策方法具有通用性和可扩展性，可为未来灾害发生后进行快速响应和高效处置提供科学化的理论指导和决策支持。

二、血液供应网络规划模型描述

(一)问题描述

本文研究的血液供应网络节点包括固定献血点、临时献血点、血站和需求点医院(图1)。献血点作为供给方，医院作为需求点，当灾害发生后的第一阶段，由于血站以及医院自身的血液储存量可能无法满足医院的需求，因此政府或应急管理部门需要根据灾害情形判断是否组织献血以及是否启用候选点增加血液供给。献血点可以分固定采血点以及临时献血点。固定献血点(如献血屋、献血车)日常存在，可以大量采血，负责血站的日常血液供应；临时献血点采集的血液量比固定献血点少，它是在灾难发生后从多个候选点中被选出而建立的。献血点将收集来的血液运送到血站进行处理。

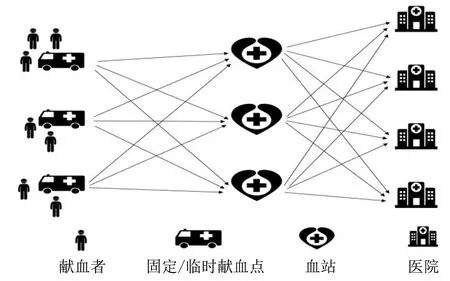
图1 血液供应网络

为了减少易腐血液的额外运输并节省生命周期的时间，将处理血液的工作集中在血站，血站会对这些血液样本进行记录、检测和分拣，并将全血通过离心分解为血液制品(如血浆、血小板和红细胞等)，在灾害发生的第二阶段，血站需要根据医院各自的需求将血液制品运送到医院。

(二)模型假设

集合：

I：固定献血点i集合，i∈I；

J：临时献血点j集合，j∈J；

K：血站k集合，k∈K；

H：医院h集合，h∈H；

M：血液制品种类m集合，m∈M。

参数：

Fj：临时献血点j的建设成本(包括献血车辆的征用以及采血设备的配置)；

B：建设费用总预算；

Op：每单位血液的采集成本(包括血袋、采血前初筛、卫生耗材，以及发给献血者的纪念物礼品等)；

Ob：每单位血液的运营成本(包括血站对血液的检测、血液成分制备、人工成本、水电费、专用设备折旧，以及一些相关的间接成本)；

Cik：每单位血液从固定献血点i到血站k的运输费率；

Cjk：每单位血液从临时献血点j到血站k的运输费率；

Ckh：每单位血液从血站k到医院h的运输费率；

ui：固定献血点i采血上限；

uj：临时献血点j采血上限；

Rkm：灾前血站k拥有血液制品m的安全库存量；

rkm：灾前医院h拥有血液制品m的安全库存量；

w：单位血液的过剩成本；

p：单位血液的惩罚成本；

φm：各种血液制品m占全血比例；

dhm：医院h对每种血液制品m的需求量。

决策变量：

Xj：临时献血点j是否被启用，是则为1，否则为0；

Oik：从固定献血点i采集全血运往血站k的数量；

Ojk：从临时献血点j采集全血运往血站k的数量；

Okhm：从血站k运往医院h各种血液制品m的数量；

Rehm：医院h处每种血液制品m过剩的数量；

Shhm：医院h处每种血液制品m短缺的数量。

目标函数：

在灾难发生后，应急管理决策者需评估血站血液储存量是否足以应对灾后急剧上升的血液需求量，并决定是否建立临时献血点扩大血液供给。因此，第一阶段的成本函数包括：临时献血点的建设成本、运输成本以及血液的采集与运营成本。第一阶段目标函数如下式所示：

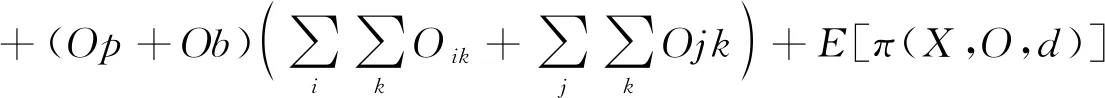
(1)

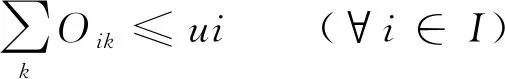
(1-1)

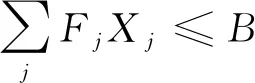
(1-2)

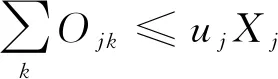
(1-3)

Xj∈{0，1},Oik(Ojk∈R+)

(1-4)

其中，约束(1-1)表示固定献血点最大血液采集量约束；约束(1-2)表示建设临时献血点不能超过预算；约束(1-3)表示只有被选择的候选临时献血点才能进行采集，同时临时献血点不能采集超过其所能采集的最大血液量；约束(1-4)为各决策变量的取值范围约束。

在决策好第一阶段临时献血点的候选位置Xj后，第二阶段的成本函数包括：短缺成本、未满足的惩罚成本以及运输成本。第二阶段目标函数如下式所示：

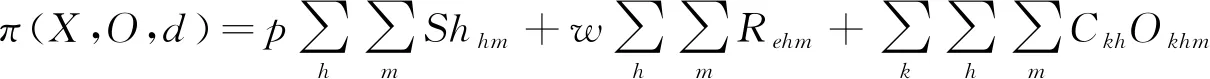
(2)

(2-1)

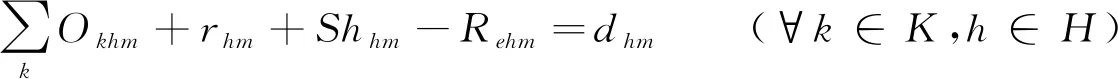
(2-2)

Okhm,Rehm,Shhm∈R+

(2-3)

其中，约束(2-1)表示血站运往医院的血液量不能超过其加工的血液量和安全库存，约束(2-2)表示每个医院血液供应、短缺、剩余之间的关系，约束(2-3)表示各决策变量的取值范围约束。

综上所述，本文分别阐述了两阶段涉及的目标函数项及约束条件，如果能精准观测到灾后医院对血液的应急需求的分布fd，那么就可以用随机规划的方法建立模型：

在血液供应网络构建时，主要困难之一是灾后的应急血液需求信息是不确定的。Wang等使用的随机规划需要大量历史数据来获取需求值的概率分布，在灾害数据极为稀缺的情况下，会增加概率分布的预测的误差，对决策的有效性会造成较大影响。(15)Wang B., Najjar L., Xiong N N., et al.,“Stochastic Optimization: Theory and Applications”,Journal of Applied Mathematics, vol.2013(2016),pp.1-2.Bertsimas等采用鲁棒优化的方法描述血液供应网络中的不确定性，但是鲁棒优化仅考虑随机变量的最坏情况，得到的决策过于保守。(16)Bertsimas D .,Brown D.B., Caramanis C.,“Theory and Applications of Robust Optimization”,SIAM Review,vol.53(2011),pp.464-501.因此在考虑完整的概率分布信息无法获取但是可以获取部分需求分布信息的情况下，本文选择Delage等提出的分布式鲁棒优化求解。分布式鲁棒旨在寻求血液需求量概率分布最糟糕情况下目标函数的最小值。(17)Delage E., Ye Y.,“Distributionally Robust Optimization Under Moment Uncertainty with Application to Data-Driven Problems”,Operations Research, vol.58(2010),pp.595-612.

(三)分布式鲁棒血液供应网络构建

采用分布式鲁棒优化得到血液供应网络模型(DRO)如下：

s.t.(1-1)～(1-4)

其中，该模型构建一个概率分布集合D，它包含需求的概率分布被称为模糊集，其中N表示训练集的规模，ε表示鲁棒参数。

(4-1)

分布式鲁棒优化寻找需求量概率分布最糟糕情况下的最优决策，其本质上还是风险中性决策，没有考虑决策者的风险偏好，然而决策者的风险偏好会对决策行为产生重大影响，因此需要对风险进行度量完善决策的合理性。

(四)基于均值-CVaR分布式鲁棒血液供应网络构建

风险价值VaR是在给定的置信度下，资产或者证券组合可能遭受的最大可能损失值，描述了相应的损失分布的分位数，但是其无法估计最大损失之外的额外损失，没有考虑极端情况，不能很好刻画尾部风险。CVaR预测了极端风险情况，描述了超过VaR值部分的超额损失的平均值，但是该方法仅考虑了低于分位数的平均收益值，忽略了高于分位数的部分，这使得决策者的决策目标偏低，整体预期利润也有所下降。因此本文采用均值-CVaR来度量风险规避的决策者。均值-CVaR工具常用于金融投资领域，它期望利润和CVaR的凸组合，最大化风险规避决策者的期望利润。运用均值-CVaR工具建立模型如下：

(5)

其中，α∈[0,1)称为风险规避因子，表示风险偏好；α=0表示风险中性；α→1表示高度规避风险。η表示置信水平α下π(X,O,d)最大的损失水平。λ∈[0,1]表示两者的权衡比重，λ=0表示决策者风险中性，0<λ<1表示预期成本与CVaR的凸组合，λ=1表示决策者高度风险厌恶。

将目标函数化简得到：

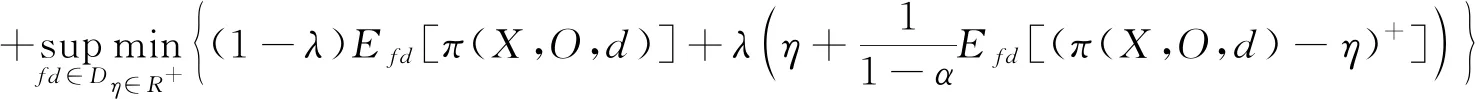
(6)

根据Efd[π(X,O,d)]的强对偶性，可得：

(7)

综上所述，两阶段分布式鲁棒优化模型可以表示为：

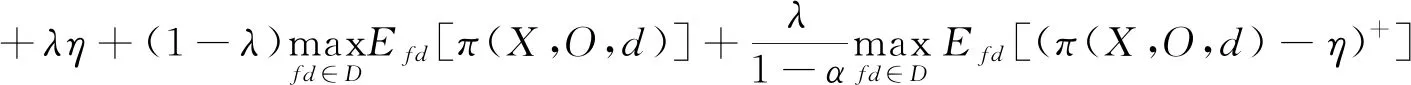
(8)

s.t.(1-1)～(1-4)

三、数值实验

本文选择使用Python第三方库rsome进行求解。rsome是一种开源Python包，用以处理各种优化问题，可以利用许多外部的最优化求解器，形成一种统一的建模求解语言，实现建模和算法二者的分离，被广泛运用于鲁棒优化和分布式鲁棒优化的求解中。(18)Chen Z., Sim M., Xiong P.,“Robust Stochastic Optimization Made Easy with RSOME”,Management Science,vol.66(2020),pp.3329-3339.本文的数值实验中运用rsome建模，调用Gurobi求解模型，平均运算时间为487.81秒。

(一)实例背景

本文以2010—2020年四川省成都市应对地震灾害为背景进行应急血液供应灾后选址问题研究(图2)。选择成都市11个区级以上的血液收集地作为固定的献血点，并选取成都市6个大型血站进行血液存储。由于血液制品种类较多，选取其中3种需求量较大的产品，分别为红细胞、血小板、血浆。选取成都市30家三甲医院作为血液需求点。

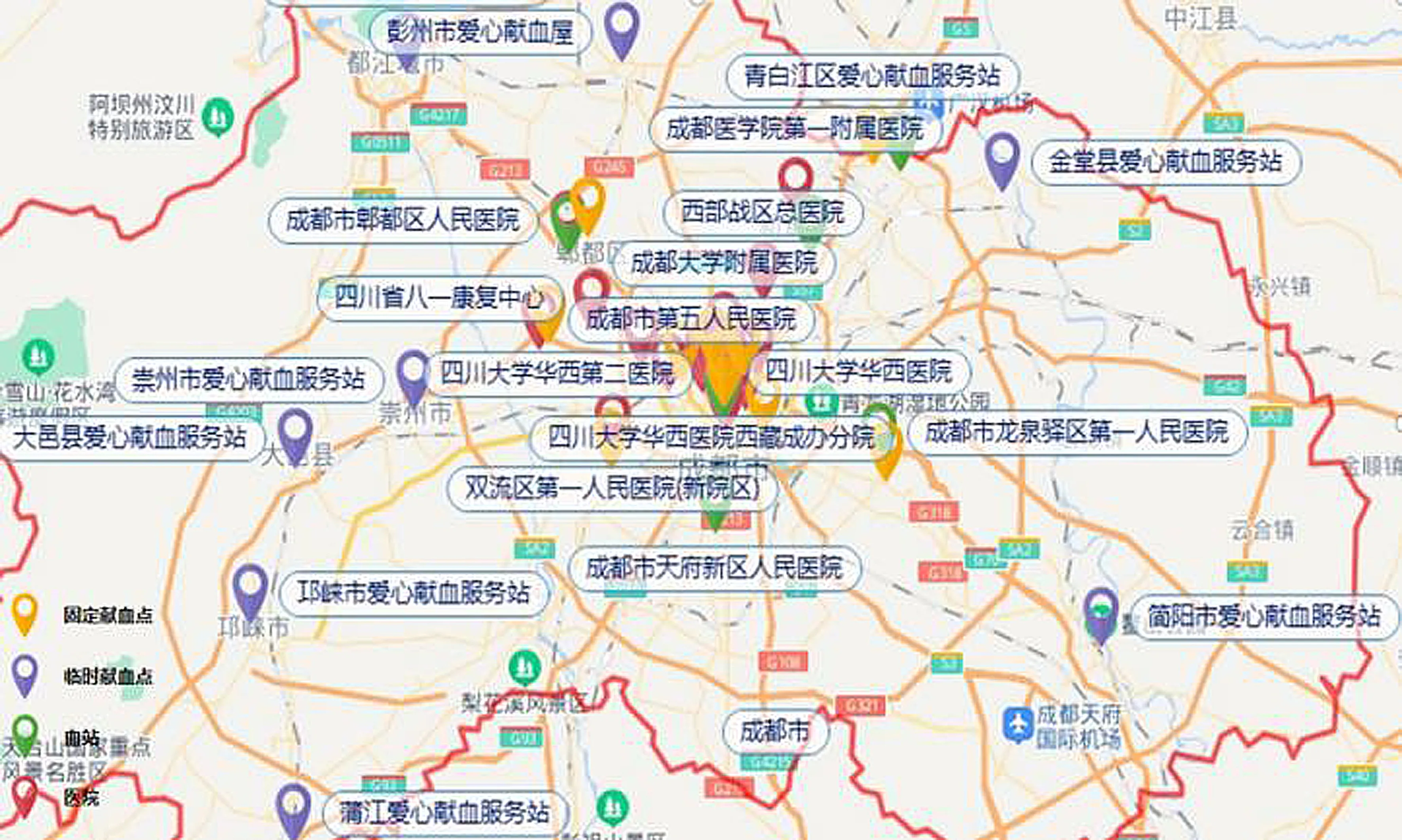
图2 案例背景

临时献血点的建设成本包括临时献血车的调用以及采血设备的使用，假设建设成本为30000元，建设成本预算为200000元。

血液的采集成本包括血袋、采血前初筛、卫生耗材，以及发给献血者的纪念物礼品等，血液的运营成本主要是血站对血液的检测、血液成分制备、人工成本、水电费、专用设备折旧，以及一些相关的间接成本。参考海南省2016年血液中心公开采供血成本数据，血液的采集成本为74.53元/U，血液的运营成本为270.09元/U。(19)王东亚：《无偿献血，为何会有偿使用？帮您算算一袋血的成本账——海南省血液中心公开采供血成本》，《南国都市报》(数字报)2016年9月28日。

成都市固定献血点有11个，位于成都市各个区，收集血液的上限与各地覆盖人口相关。根据国家卫健委公布的2020年人均献血率为1.12%，人均献血量在300ml—400ml之间，各固定献血点献血量上限如表1所示。

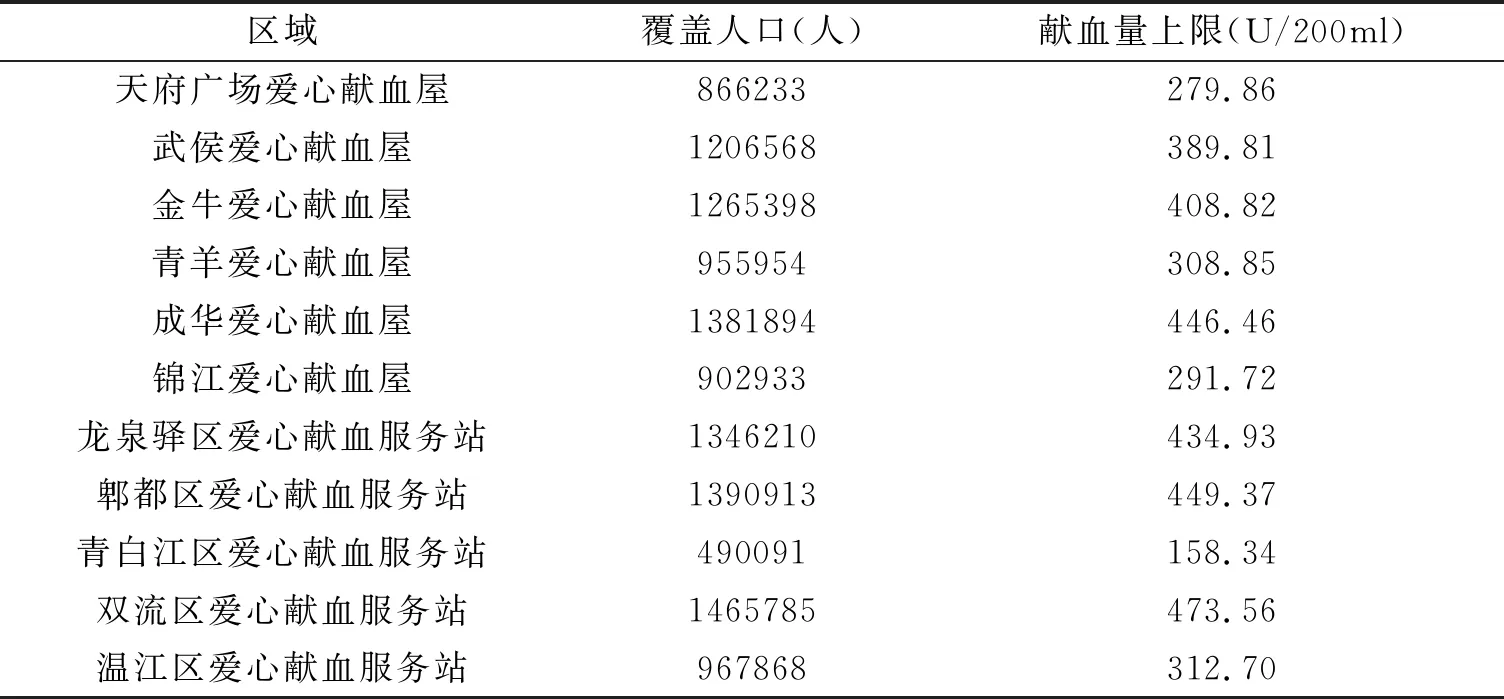
表1 献血量上限

成都市临时献血点候选地有8个，位于成都市各市以及县，各临时献血点献血量上限如表2所示。

表2 献血量上限

根据Kochan等的研究，灾后的单位血液短缺成本数据为857元/U，灾后多余血液单位处理成本为361.15元/U。(20)Kochan C.G., Kulkarni S.S., Nowicki D.R.,“Efficient Inventorying and Distribution of Blood Product During Disasters”,in Advances in Managing Humanitarian Operations. Springer,Cham,2016,pp.185-204.各血液制品占全血比例如表3所示。

表3 血液制品占全血比例

(二)计算结果

通过改变参数α和λ的值可以衡量不同决策者风险规避的程度。本文设置鲁棒参数ε=10*N-1/10，比较不同α和λ下，对总成本的影响(图3)。

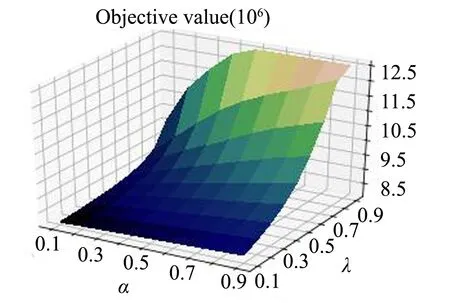
图3 不同风险规避程度下总成本比较

将临时献血点彭州市、都江堰市、崇州市、大邑县、邛崃市、蒲江县、简阳市、金堂县分别标记为候选地(1)—(8)。不同α和λ下，选择启用的临时献血点如表4所示。

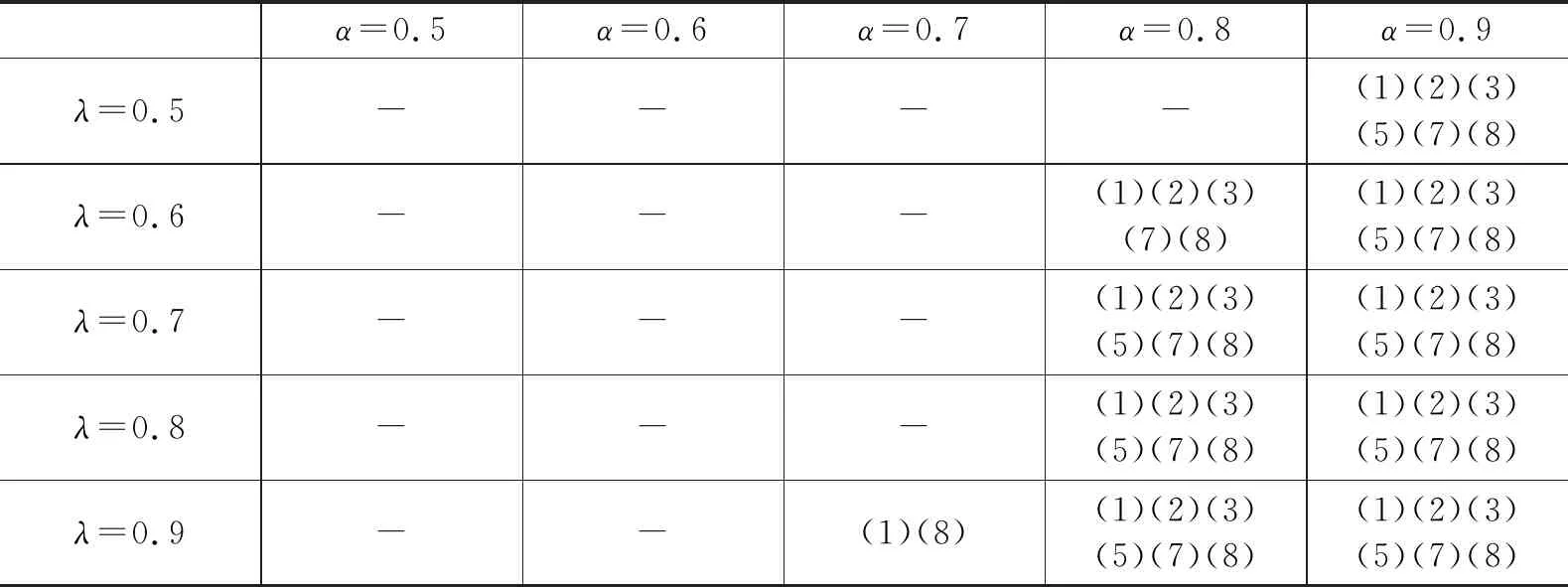
表4 不同风险规避程度下启用临时献血点

通过图3以及表4可知，当权衡比重λ下降时，DRO模型的最佳目标值减小，因为CVaR在目标函数中的比例变小。随着决策者风险厌恶程度的上升(即α上升)，灾后血液供应网络总成本开始逐步上升，并且随着候选地址的逐步开放，总成本开始趋向平稳，直到α→1,此时决策者高度厌恶风险，得到过度保守解，成本达到最高。在预算范围内启动所有的候选地点包括：彭州市、都江堰市、崇州市、邛崃市、简阳市、金堂县。从地理位置上来讲这些地方不仅距离血站较近，同时人口基数较多可以收集更多的血液。

通过改变α和λ的值进一步测试期望值与CVaR之间的变化，通过图4及图5可知，风险规避程度高的期望成本(即α较高)总是高于风险规避程度低的期望成本，CVaR的趋势也同样如此，从λ=0.5之后期望成本开始达到平稳状态，此时启用所有候选地址，并且在较高的风险规避程度下，权衡比重λ对成本的影响更为突出。

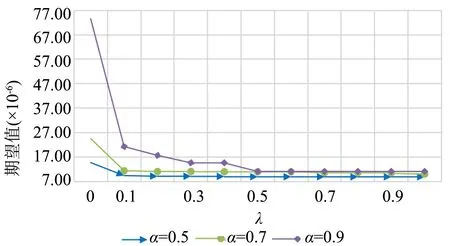
图4 不同风险规避程度下期望成本比较

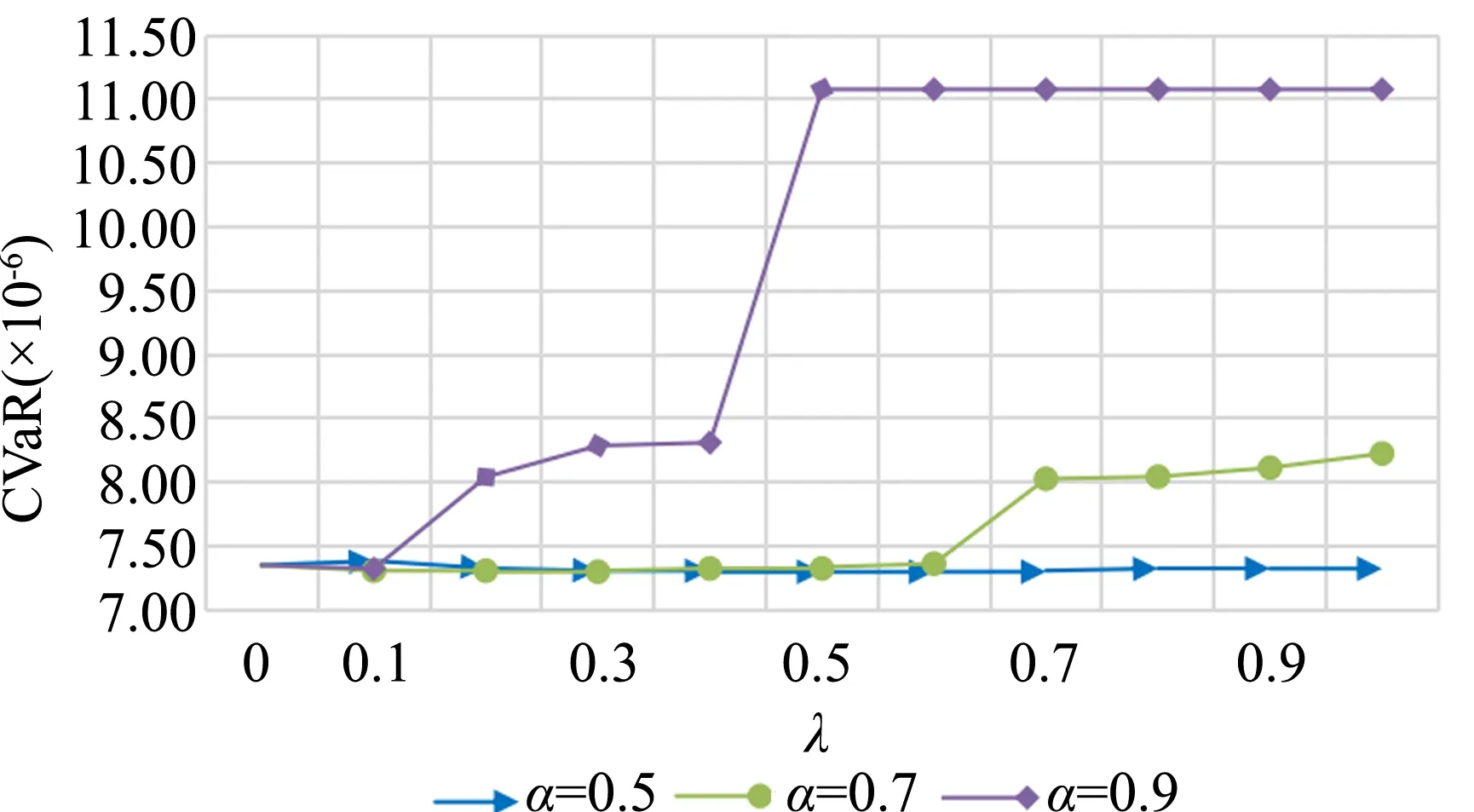
图5 不同风险规避程度下CVaR比较

设置鲁棒参数ε=10*N-1/10，α=0.7，λ=0.9下分布式鲁棒模型供给医院血液数量为DRO*，鲁棒优化模型为RO*，随机优化模型假设不确定需求分布为均匀分布设为SP*(表5)。本文设置5个训练集，各医院需求量为DEM*，计算各模型平均需求未满足量GAP，令由表5以及图6、7、8可以看出使用分布式鲁棒优化模型可以显著降低血液产品的未满足率。鲁棒优化模型由于其过度保守性，会选择在最坏情况下进行决策，因此在供给不足的情况下，该模型选择将产品优先供给其中几个医院，导致其他医院需求未满足率上升，因此在该优化模型下平均未满足率较高。随机优化模型相较于分布式鲁棒优化模型，在降低红细胞未满足率上性能相似，但是在优化血小板以及血浆的未满足率上有显著提升。

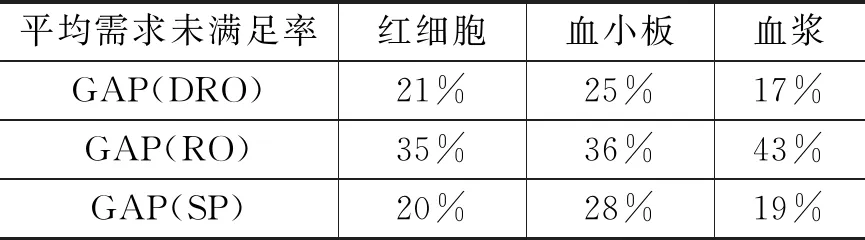
表5 各模型下各产品需求未满足率

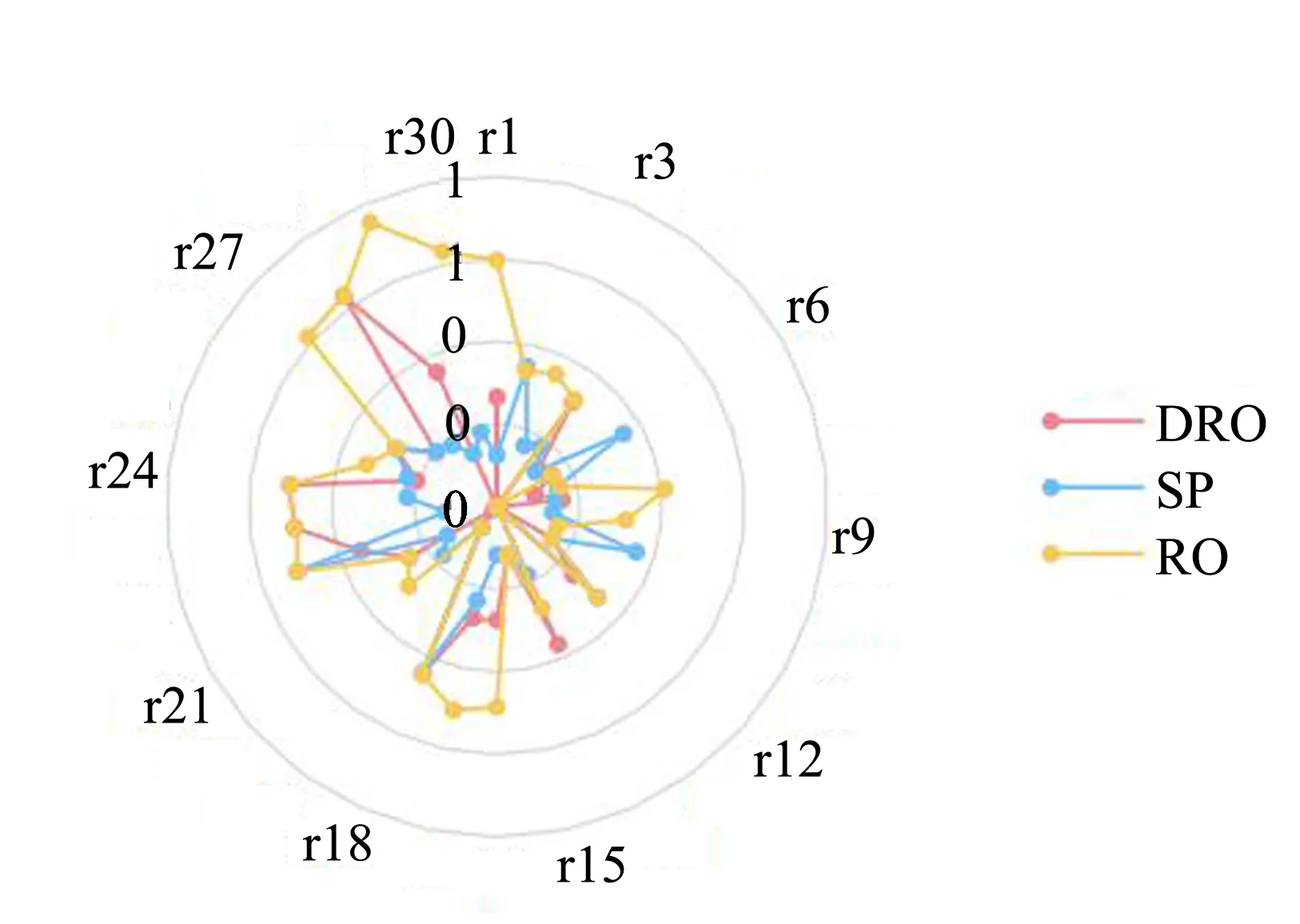
图6 不同模型下各医院红细胞平均未满足率

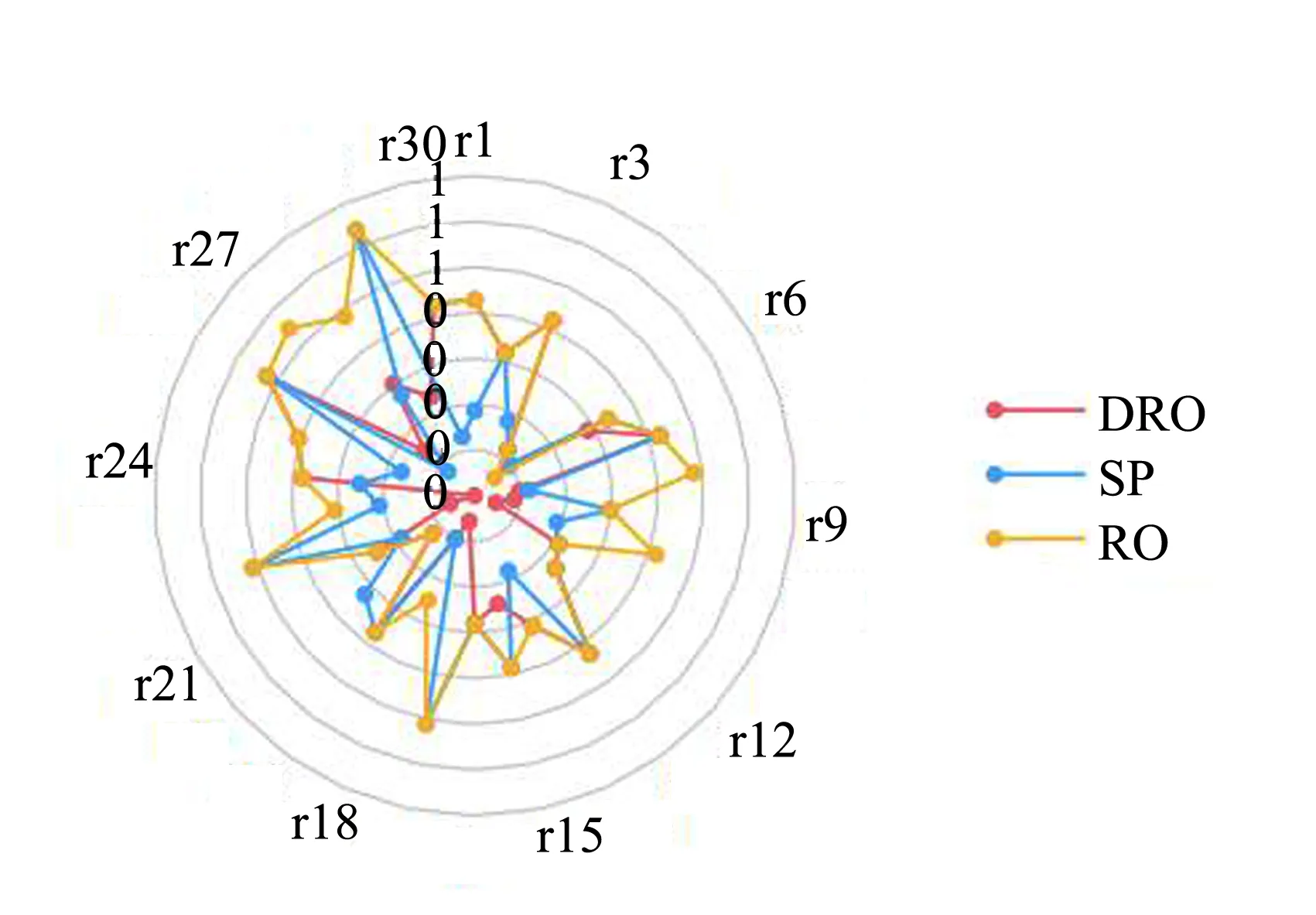
图7 不同模型下各医院血小板平均未满足率

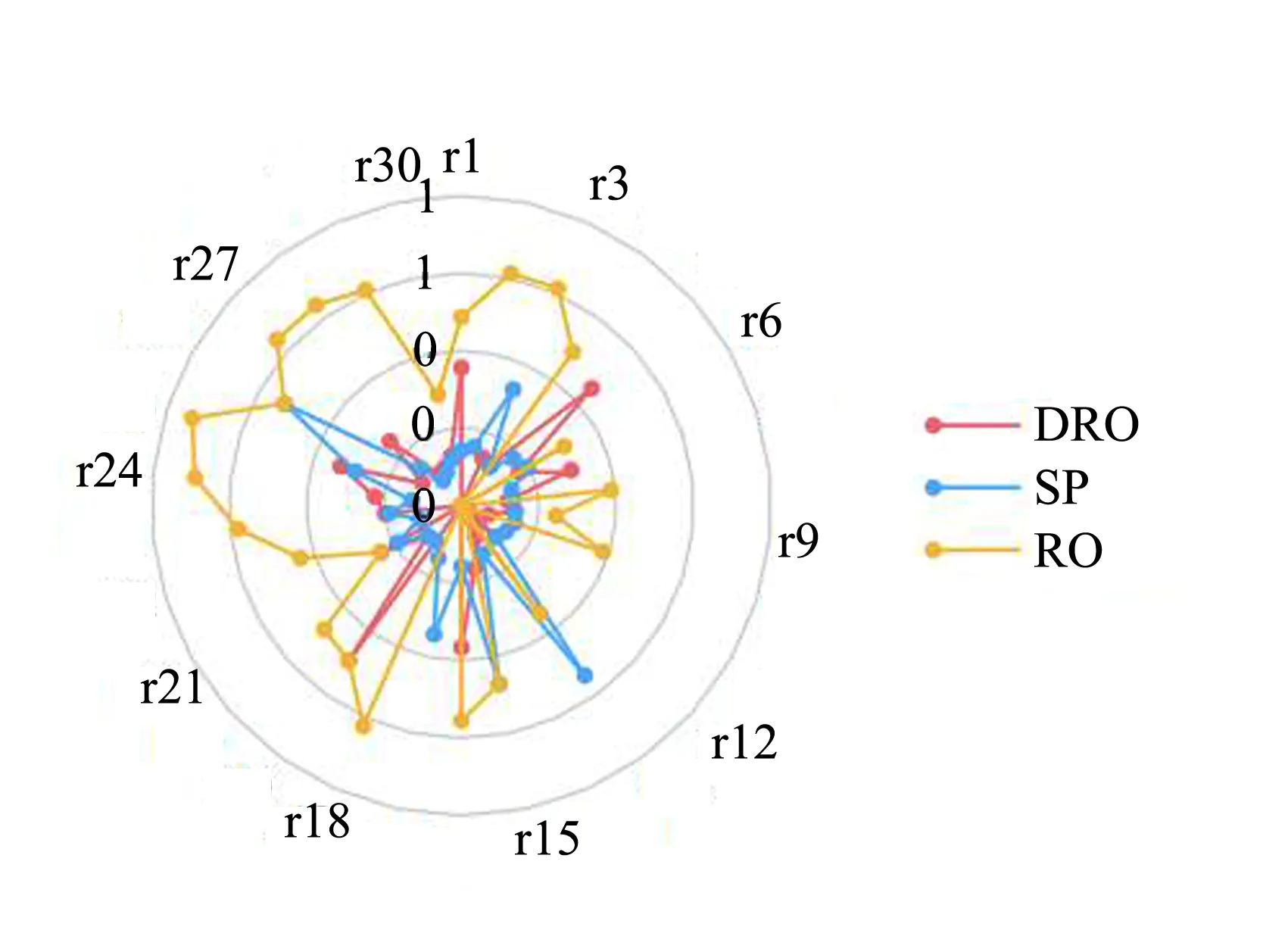
图8 不同模型下各医院血浆平均未满足率

四、总结

在灾后安全救援的过程中对血液需求进行预测是十分困难的。但为了保证血液的充足供应，盲目加大采血不仅会增加过剩血液的报废成本，而且会加重社会负担，造成血液资源的浪费。本文考虑大规模自然灾害事件发生后应急血液需求具有不确定性的特点，利用分布式鲁棒优化处理不确定性，达到模型鲁棒性与经济性之间的均衡，同时引入均值-CVaR工具来度量风险规避的决策者。应急决策者可以根据自身风险承受能力选择相应的方案，为应急救灾工作提供参考和决策支持。

未来将考虑血液的更多特性，例如多种类型血液之间的互相替代性、血液供应不稳定等特性，以及地震灾害下资源成本、路径中断等不确定性，并结合灾害强度以及受灾可能性，进行应急血液供应链网络选址问题的后续研究。