突发疫情下考虑优先级和动态需求的应急物资配送

庄伟卿 吴 琼

(1. 福建工程学院互联网经贸学院， 福建福州 350014；2. 福建工程学院交通运输学院， 福建福州 350118)

一、引言

突发事件应对是人类社会面临的共同难题。近十年，在全球范围内爆发了多种公共卫生事件，对人类生命与财产安全造成了巨大损失。(1)段容谷、庄媛媛、张克勇、吴云霞：《突发公共卫生事件下多阶段应急救援物资配置研究》，《中国安全生产科学技术》2021年第12期。2019年末一场新冠肺炎疫情突袭武汉，随后蔓延至全国，形势严峻，特别是疫区出现了应急救援物资紧缺的问题。鉴于此，合理预测各地区物资需求量并实施科学高效的配送策略解决应急物资短缺问题，对疫情防控有着重大的意义和积极作用。

目前，国内外关于应急物资配送的研究相对成熟。刘春林等是我国较早研究应急调度问题的学者，其根据应急系统中多个救出点的特点，引入连续可行方案的概念，以最早应急开始时间为目标构建模型。(2)刘春林、盛昭瀚、何建敏：《基于连续消耗应急系统的多出救点选择问题》，《管理工程学报》1999年第4期。此后，学者们从不同的研究角度构建不同的应急物资配送模型。张杏雯等兼顾应急物资配送的效率与公平，引入公平理论构建多目标模型。(3)张杏雯、倪静：《公平约束下的应急物资配送模型及算法》，《统计与决策》2020年第7期。Theeb等从人道主义角度出发，不仅研究了应急物资的配送问题还研究了伤员撤离和救护人员指派的问题，并采用拆分配送的方式解决。(4)Nader Al Theeb,Chase Murray,“Vehicle routing and resource distribution in postdisaster humanitarian relief operations”,International Transactions in Operational Research,vol.24，no.6(2017),pp.1253-1284.一直以来，不确定性作为应急物流的重要特征之一，备受学者们的关注。Arda考虑了供应、需求以及路网的不确定性情况，建立了两阶段随机规划模型。(5)Arda G.B.,“A two-stage stochastic programming framework for transportation planning in disaster response”,Journal of the Operational Research Society,vol.55,no.1(2004),pp.43-53.管峰等证明了需求属于有界集合，构建两种有界集合下的鲁棒优化模型，并与确定性模型的目标函数值对比，验证其可行性。(6)管峰、钟铭、韦达：《需求不确定的车辆路径鲁棒优化模型》，《上海海事大学学报》2015年第4期。刘长石等考虑了地震灾害后应急物流设施不确定失效的情况，采用情景建模方法构建多目标配送路径模型。(7)刘长石、瞿艳平、罗亮、周鲜成：《震后应急物流设施不确定失效情景下的LRP研究》，《模糊系统与数学》2019年第5期。Bozorgi-Amiri等考虑了受灾点需求、应急物资储备中心和供应量不确定的情况，将成本视为不确定参数，建立了路径优化模型。(8)Bozorgi-Amiri A.,Jabalameli M.S.,Mirzapour Al-e-Hashem S.M.J.,“A multi-objective robust stochastic programming model for disaster relief logistics under uncertainty”,Operations Research-Spektrum,vol.35,no.4(2013),pp.905-933.王小纯等用模糊机会约束条件表示震后应急物资需求和路网的不确定性，建立了多时间段多目标的应急物资分配-运输规划模型。(9)王小纯、牟海波：《震后应急物资分配-运输问题研究》，《铁道科学与工程学报》2021年第4期。Florio等研究了具有随机需求和给定概率下运输持续时间约束的车辆路径问题，并设计新的算法来求解。(10)Florio A.M.,Hartl R.F.,Minner S.,Salazar-González J.J.,“A branch-and-price algorithm for the vehicle routing problem with stochastic demands and probabilistic duration constraints”,Transportation Science,vol.55,no.1(2021), pp.122-138.田军等将不确定的物资量用三角模糊数来表示，并用函数模拟真实路况建立多目标配送模型。(11)田军、马文正、汪应洛、王刊良：《应急物资配送动态调度的粒子群算法》，《系统工程理论与实践》2011年第5期。张景玲等针对动态需求问题建立了“预优化路线调度”和“实时动态调度”两阶段数学规划模型，并给出了求解策略。(12)张景玲、赵燕伟、王海燕、介婧、王万良：《多车型动态需求车辆路径问题建模及优化》，《计算机集成制造系统》2010年第3期。张玉州等以历史需求为参考，建立了需求服从泊松分布的物资配送模型。(13)张玉州、张子为：《考虑动态客户需求的物资配送问题求解方法》，《西安交通大学学报》(社会科学版)2020年第8期。孙华丽等考虑了随机需求同时又考虑了路况的不确定性，设计了随机机会约束的配送路径模型(14)孙华丽、周战杰、薛耀锋：《考虑路径风险的不确定需求应急物流定位-路径问题》，《上海交通大学学报》(哲学社会科学版)2013年第6期。；孙华丽等进一步运用鲁棒优化理论将路径风险定量化建立了双目标多物资定位-路径优化模型，采用遗传算法对其求解(15)孙华丽、曹文倩、薛耀锋、王循庆：《考虑路径风险的需求不确定应急物流定位-路径问题》，《运筹与管理》2018年第7期。。

综上，现阶段关于需求不确定的车辆路径问题求解，一般的处理方式是使用区间数、模糊数或者假设需求服从一定分布。这样的方法可能导致估计的需求误差较大，且没有针对性。因此，本文以大型突发性疫情为研究背景，聚焦新冠肺炎疫情案例，分析突发疫情的特点，结合疫情实际情况改进传染病传播动力学模型解决需求不确定的问题。本文结合层次分析法与灰色关联法对需求点进行优先级分级，并运用到应急物资的配送模型中，使模型更具有针对性以及实用性。

二、不确定需求预测及优先级确定

(一)问题描述

突发疫情是指短时间内在特定地区的人群中大量传播，且严重损害公众健康的疾病疫情。(16)李颖祖：《基于服务水平的突发疫情应急物流网络优化设计研究》，硕士学位论文，南京理工大学，2019年。突发疫情属于突发公共卫生事件的一部分，具有突发性、公共性以及危害复杂性和严重性的特点。突发疫情后的应急物资配送问题是应急管理的重要组成部分，由于突发疫情通常影响面积大、持续时间长且阶段区分明显，所以该背景下的应急物资配送问题具有配送需求点多、应急物资筹集方式多、调度范围广且需求不确定的特点。

突发疫情后的应急物资主要包括生活类物资和医疗类物资。这两种物资的需求都与患者人数和医护人员数量相关。其中医护人员数量是确定的，需求不确定主要体现在不同的疫情阶段物资需求量随患病人数呈现动态变化的现象。因此，在疫情发展过程中，提前预测出患病人数并通过医疗经验获得每位患者的单位需求情况，便可以提前预测疫区的需求情况并进行合理物资配送，以保证救援的高效进行。

(二)不确定需求预测

1. 模型改进说明

传染病动力学模型常用于研究疫情发展变化过程和传播规律、速度、空间等问题，为传染病的预防控制提供决策依据。但现有的传染病动力学模型不适用于COVID-19，所以本文选择更贴近传染病真实传播规律的SEIR模型。(17)罗丹婷、钱华、刘聪、黄顺祥：《不同国家和时段COVID-19控制策略效果评价：基于自适应PSO-SEIR模型》，《科学通报》2021年第Z1期(18)曹广、沈丽宁：《基于SEIR模型的网络医疗众筹传播建模与仿真分析》，《数据分析与知识发现》2022年第1期。本文结合COVID-19特点对以下几方面作出改进：

(1)在模型中体现出隔离现象，COVID-19存在潜伏期长的特点，所以存在隔离以及医学观察的人群;

(2)COVID-19存在无症状感染者，因此，未被发现的无症状感染者作为传染源传播疫情的几率变大;

(3)COVID-19存在复阳现象，在改进模型中体现出一定比例的治愈患者重新变为感染者的现象。

综上所述，本文根据COVID-19的特点对SEIR模型进行改进，预测出对应急物资有需求的隔离潜伏者和住院患者两类人群数量，以达到预测应急物资需求的目的。

2. 模型假设

假设1：不考虑人口的自然出生率和死亡率；

假设2：各疫区人口情况稳定，即不考虑人口流动；

假设3：隔离易感染者中未携带病毒的人在 14 天(医学观察期为 14 天)后将变为易感者，该假设会产生一定的误差，在后面模型中会做处理；

假设4：治愈患者除一定概率的自身“返阳”外，不再被传染。

3. 符号说明

S：易感者；SQ：隔离易感染者；E：潜伏者；EQ：隔离潜伏者；I：感染者；IQ：住院的感染者；D：死亡者；R：康复者；ρ：隔离比例；σ：接触率；ε：潜伏者的发病概率；β：感染率；q：解除隔离速率，这里取q=1/14；θ：隔离潜伏者向隔离感染者转化的速率；δ：感染者中死亡的概率；γ：感染者中被治愈的概率；ω：感染者被发现隔离的概率；α：康复者复诊转变为阳性的概率；K={1,2,…,k}：疫区的集合；J={1,2,…,j}：医疗物资供应点集合；T={1,2,…,t}：整个疫情持续的时间集合；Nk(t)：在t时刻疫区k的人口总数；Sk(t)： 在t时刻疫区k未被隔离的易感染者数量；Ek(t)： 在t时刻疫区k未被隔离的接触者数量；Ik(t)： 在t时刻疫区k未被隔离的感染者数量；SQk(t)： 在t时刻疫区k被隔离的易感染者数量；EQk(t)： 在t时刻疫区k被隔离的接触者数量；IQk(t)： 在t时刻疫区k被隔离的感染者数量；Rk(t)： 在t时刻疫区k的康复者数量；Dk(t)： 在t时刻疫区k的死亡者数量；dk(t)：疫区k在t时刻对应急物资需求量。

4. 模型建立

根据疫情的实际情况将人群分为以下几类，其关系如图1。疫情期间数据通常是每日一报，为了简化步骤将公式转化为差分方程组形式，如公式(1)—(7)所示。

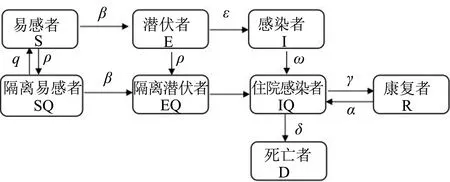
图1 改进SEIR

(1)

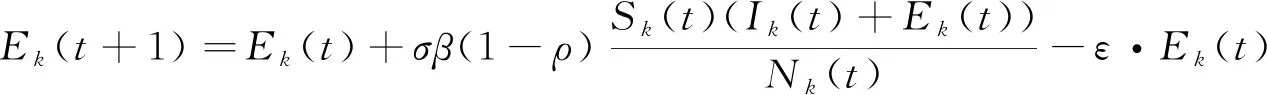
(2)

Ik(t+1) =Ik(t)+εEk(t)-(ω+δ)Ik(t)

(3)

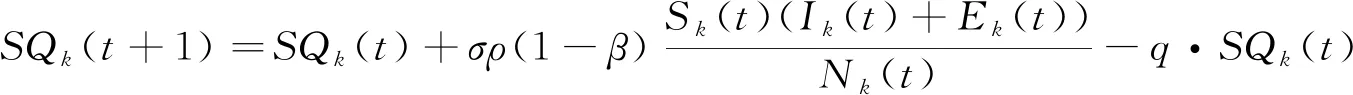
(4)

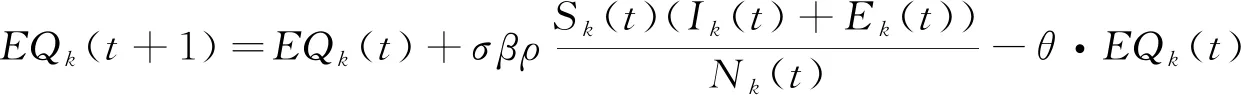
(5)

IQk(t+1)=IQk(t)+ωIk(t)+θ·EQk(t)-(δ+γ)·IQk(t)+αRk(t)

(6)

Rk(t+1) =Rk(t)+γ·IQk(t)-αRk(t)

(7)

式(1)描述了疫区k中未被隔离易感者人数的变化情况。易感者中一部分接触感染者被隔离变成隔离的易感者，未被发现的被感染的易感者变为未被隔离的潜伏者，而隔离的易感者中未被感染的经过14天隔离后重新变回易感者。

式(2)描述了未被发现进行隔离的潜伏者人数的变化情况。未被发现的潜伏者来自接触感染者的易感者，其有ρ概率被发现进行隔离变为隔离潜伏者，一部分过了潜伏期发病变为感染者。

式(3)描述了未被隔离的感染者数量的变化情况。其来自未被发现的潜伏者，该部分人群有ω的概率被发现后隔离治疗。

式(4)描述了隔离易感者的数量变化情况。其中一部分被发现变为隔离潜伏者，另一部分隔离期满变回易感者。

式(5)描述了隔离潜伏者的数量变化情况，全部被转至医院治疗。

式(6)描述了住院患者的数量变化。

式(7)描述了康复后的患者有α概率重新复阳。

当给定初始值Sk(0)，Ek(0),Ik(0),SQk(0)，EQk(0)，IQk(0)，Rk(0)等相关参数，便可以由以上公式预测疫区k中各类人数情况，对需求作出预测。

将物资分为消耗类物资和非消耗类物资。其中消耗类物资是救援人员和患者共同需要的，且用过一次后不能再次使用，例如生活物资以及口罩类消耗型医疗物资。而非消耗类物资这里主要指医疗器材，所以考虑以往库存量Aj，如式(8)所示。

需求预测公式如(9)所示。N(t)：该地区医护人员数量；Nj：所有人员对j的平均需求量；Ej：潜伏期人员对第j类物资的需求标准；Ij：住院患者对第j类物资的需求标准。

(8)

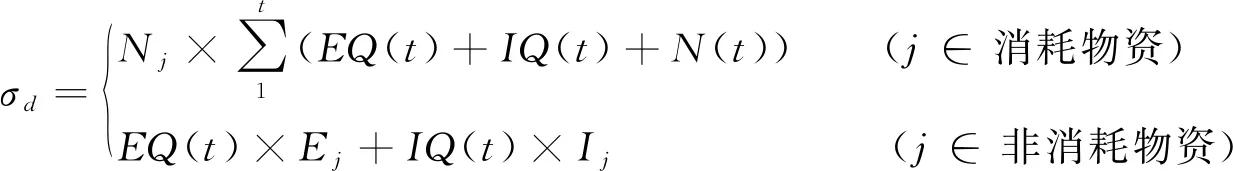
(9)

式(10)是指由于前述假设3会导致误差的产生。因为在未到14天前，患者及隔离潜伏者每天都会消耗资源，如果按照每天1/14的比例计算退出，大致误差为7.43%。这样容易产生感染上升期物资预测不足、感染下降期物资预测富余的误差，所以这里作出上升期需求增加10%、下降期减少10%的处理。

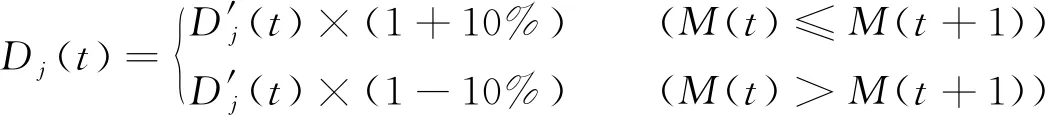
(10)

(三)优先级计算

灰色关联度分析法是一种基于灰色系统理论的方法，通过对系统的动态发展过程进行定量分析，考察各指标间的关联性。但其将所有因素对总目标的影响大小视作等同，没有考虑指标权重的问题。所以本文选择AHP/灰色关联法相结合的方法，充分利用两个方法的特点与优势，对疫区需求紧迫情况进行判断。依据研究背景选取评价指标，首先考虑到疫情物资的需求紧迫度与该疫区的患者人数和潜伏者人数有着很大的关系，其次与疫区的人口密度、疫区GDP，以及因疫情死亡人数都有一定的关系，所以选择这五项影响因素作为评价指标。首先运用AHP方法对影响因素进行专家打分确定权重，然后选取每个评价指标中最大值作为母序列计算每个指标值与母序列的关联度，关联度大的优先配送，具体计算过程见案例部分。

三、突发疫情的应急物资配送模型

(一)模型假设

(1)假设候选的物资集散点和疫区需求点的位置已知，应急物资直接物资集散点供给各疫区需求点；

(2)假设运输工具的标准相同且数量和容量有限，速度已知；

(3)假设运输工具从物资集散点出发，最后配送任务完成后返回该节点；

(4)假设同一节点只接受一辆车服务；

(5)假设装卸货时间固定且相等；

(6)假设服务完的车辆物资不够服务下一个需求点便不再服务。

(二)变量说明

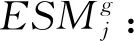
(三)模型建立

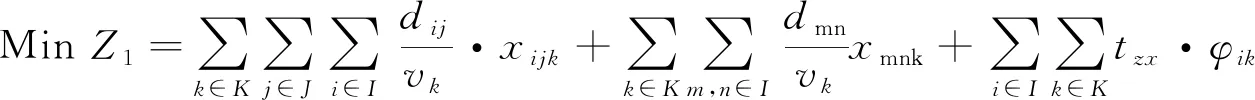
(11)

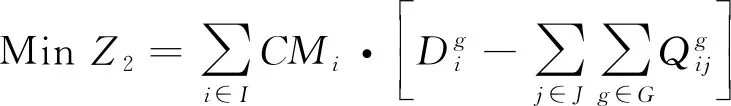
(12)

目标式(11)表示应急物资运输时间最小化，主要包括从集配中心到各个需求点最终返回集配中心的时间，以及装卸货时间。

目标式(12)表示应急救援系统的损失最小，主要与需求点的需求紧迫度和应急物资未满足量有关。

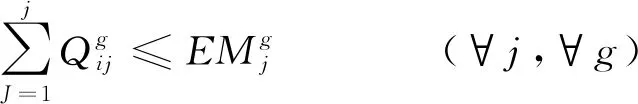
(13)

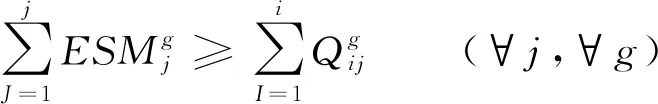
(14)

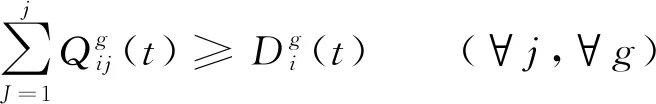
(15)

式(13)—(15)为物资流约束，式(13)表示从应急物资集配中心j流出的应急物资量不得大于其供应给各需求点的量的总和。式(14)表示集配中心j的全部可用的应急物资量应该大于该集配中心的物资流出量。式(15)各需求点的物资流入量应不低于其需求量。

(16)

(17)

式(16)—(17)为车辆流约束，式(16)表示从集配中心j到需求点i实际使用的运载工具数量应是能承载该运输量的运输工具的最小值。式(17)表示集配中心j实际使用的运载工具数量应不超过该地的运输能力。

(18)

式(18)是非负约束，表示各周期内各条路径上的物资配送量应为大于等于零的数。

(四)模型适用性说明

考虑优先级和动态需求的应急物资配送模型，适用于新冠肺炎疫情各时间阶段的各地区的应急物资配送。不同时间阶段的特点可以从需求预测模型中的改进SEIR模型参数选择体现，最终pareto解也是根据疫情的不同阶段背景确定两目标权重值选择最优解。SEIR模型是根据新冠肺炎疫情的特征进行改进的，因此应急物资配送模型仅适用于新冠肺炎疫情背景下的应急物资配送，其他情况可根据实际重新设计SEIR模型。

(五)求解方法

本文选择精英保留策略的非支配排序遗传算法(NSGA-II)求解模型。该算法使优秀的个体进行遗传进化，与传统的遗传算法相比具有更好的收敛性和稳定性，性能方面也更加优异。算法具体设计如下：

第一步，编码和初始方案设计。选择实数编码，随机生成初始群体。

第二步，拥挤度计算。先根据每个个体的目标函数值计算非支配等级，再计算每个等级的个体的拥挤度。

第三步，遗传操作。选择算子：选择锦标赛法结合等级和拥挤度选择下一代；交叉算子：选取子路径交叉法；变异算子：选择 2-opt组合优化邻域算子作为变异算子，2-opt与VNS算法都是局部搜索算法，2-opt优化算子提升收敛速度再加入变邻域智能搜索算法快速收敛于全局最优解。

第四步，参数设计。通过不断地调试设置参数如下：种群大小PopSize =100，最大迭代次数IterMax =300，交叉概率CrossProb=0.6，变异概率MutaProb=0.1，最大的非劣解数Threshold=100。

四、案例分析

(一)算例设计

本文选取武汉市2020年2月22日—2020年3月8日疫情情况为背景案例验证模型。此时政府分批征用26家医院作为全市定点医疗机构。经查阅资料将国际博览中心A馆和慈善总会的仓库武汉市黄陂区天横三路黄承烈湾疫情防控捐赠物资联合应急仓库作为物资集散地。假设这两处物资集散地为武汉市26家定点医院提供4种应急物资应急医疗物资配送。车辆统一规格，最大载重量为3000kg，车辆的平均行驶速度v=35千米/小时， 每辆车平均装卸货时间为0.5小时，假设两个集配中心各有货车10辆。

表1 应急物资种类与规格

以2月22日作为第一周期，准备未来5天的应急需求物资配送至各需求点，通过百度地图测量到各集散中心与需求点的坐标，由于篇幅限制没有列出。用j1-j2表示应急物资集散中心，i1-i26表示26个需求点。物资的规格及单位需求等情况如表(1)—(3)所示。

(二)需求计算

首先计算需求情况，根据案例所处疫情时期设置参数如表4所示。

表2 应急物资单位需求 (单位：每人每天)

表3 各集配中心应急物资量

表4 改进SEIR模型参数赋值

人口中能接触到感染者或潜伏者的人数并非全部人口，经查阅知该数值约为200万。住院患者数可由武汉市卫健委发布的床位信息得到，但由于需求点范围太小其他数据查阅不到，所以本文先预测各行政区人数，使用公式(19)求得各行政区隔离潜伏者数(19)邹彦琳、梁进：《SEIR修正模型下的武汉地区COVID-19疫情研究与分析》， 《运筹与模糊学》2020年第3期。，再通过开放床位比例求得各需求点的隔离潜伏者人数，得到2月22日初始数据后预测十五日的人数变化情况。武汉共13个行政区，这里仅展示部分预测图，计算预测值与实际值的相对误差如图2和图3所示。计算得洪山区隔离潜伏者人数预测平均相对误差3.63%，武昌区隔离潜伏者人数预测平均相对误差3.77%，预测精准度较高。根据表(2)及需求预测公式(8)—(10)计算各需求点需求量如表5所示。

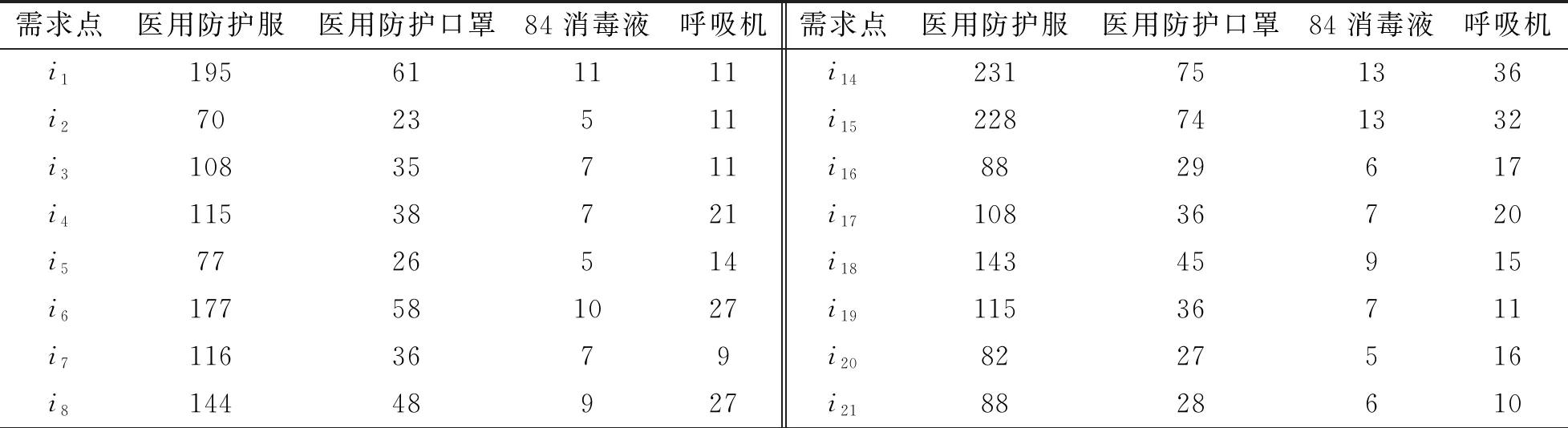
表5 各行政区物资需求数据

续表5

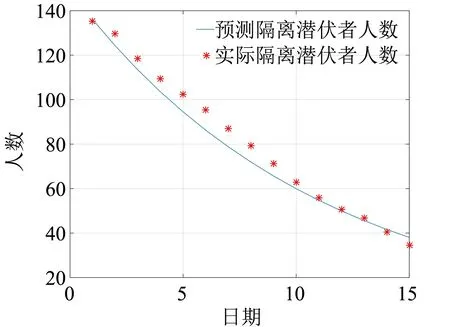
图2 洪山区隔离潜伏者预测值与真实值对比

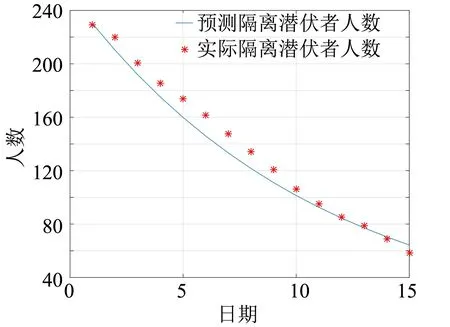
图3 武昌区隔离潜伏者预测值与真实值对比

En=(In+5+IQn+5+Rn+5+Dn+5)-(In+IQn+Rn+Dn)

(19)

(三)优先级计算

计算各需求点的优先级排序情况。将五个指标进行专家打分构造判断矩阵计算权重。在进行专家打分时，遵循从国家和社会角度出发进行评估的原则，并参考吕伟婧对新冠肺炎疫情的影响因素分析(20)吕伟婧：《社会学视角下的新型冠状病毒肺炎疫情影响因素分析及预测》，博士学位论文，延边大学，2021年。，以确保打分的合理性。由于篇幅限制打分矩阵不再给出，权重计算结果如下：患者人数0.4935，潜伏者人数0.3041，人口密度0.0576，GDP 0.0317，因疫情死亡人数0.1132。对判断矩阵进行一致性检验，求得λmax=5.2913, CI=0.0728, CR=0.0650. CR<0.1,说明权重分配合理。这里给出各区评价指标数据，如表6所示。

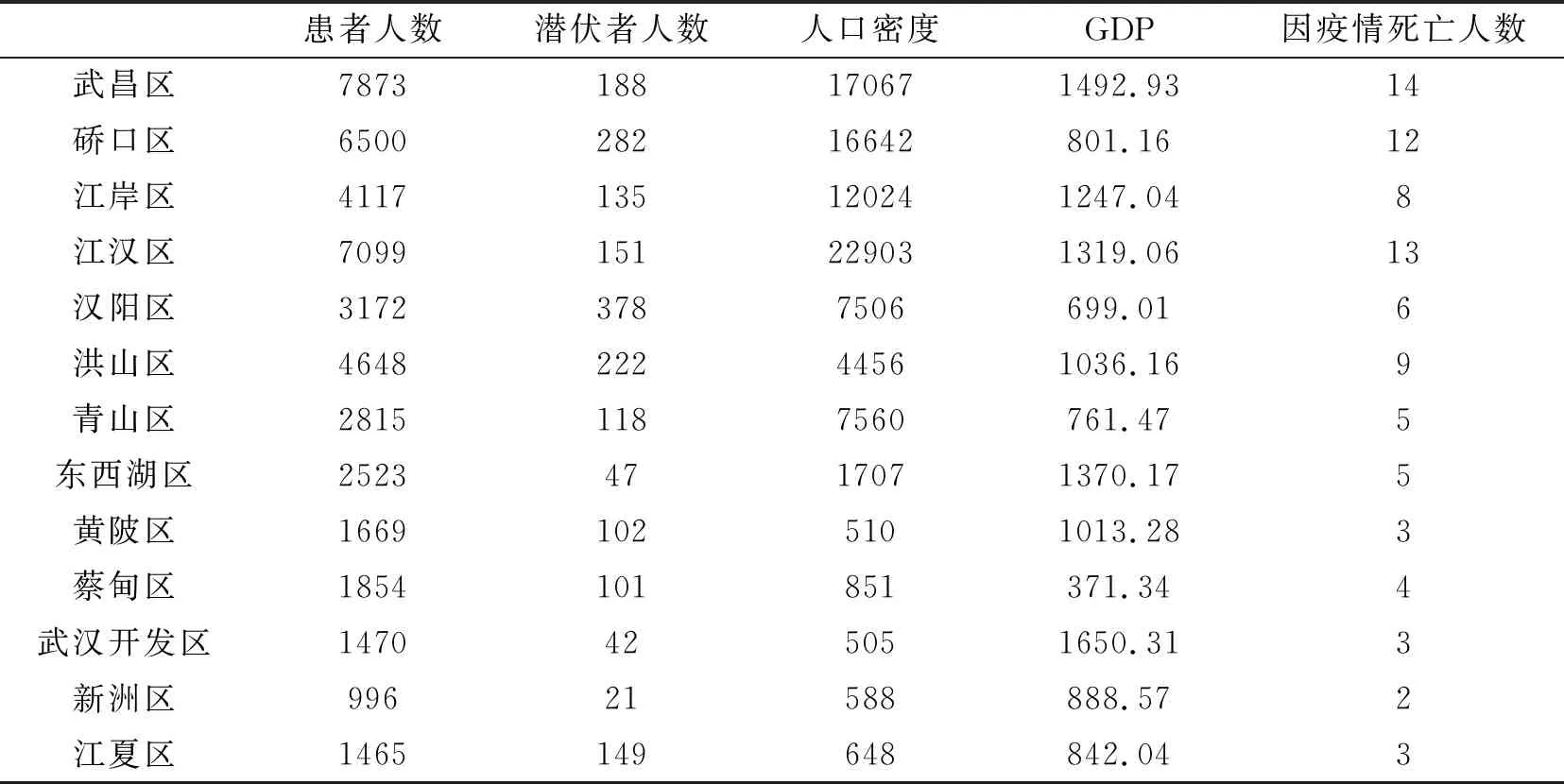
表6 武汉市各行政区评价指标数据

对数据进行无量纲处理，选择最大值作为母序列计算关联度值并进行排序。得到优先级排序为武昌区、江汉区、硚口区、汉阳区、洪山区、江岸区、青山区、东西湖区、江夏区、蔡甸区、黄陂区、武汉开发区、新洲区。此时得到的优先级是行政区优先级，随后以行政区优先级、住院患者数、隔离潜伏者数为指标重复以上操作对需求点优先级进行排序，如表7所示。

表7 需求点优先级排序

(四)模型求解

使用NSGA-II算法，在MATLAB软件中迭代300次，最终获得32个非劣解，由图4和图5可以看出两个目标值最后趋于平稳，说明收敛完成。

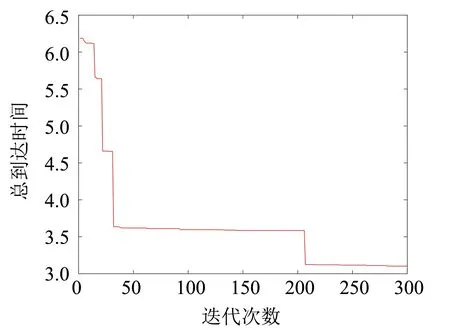
图4 目标1迭代

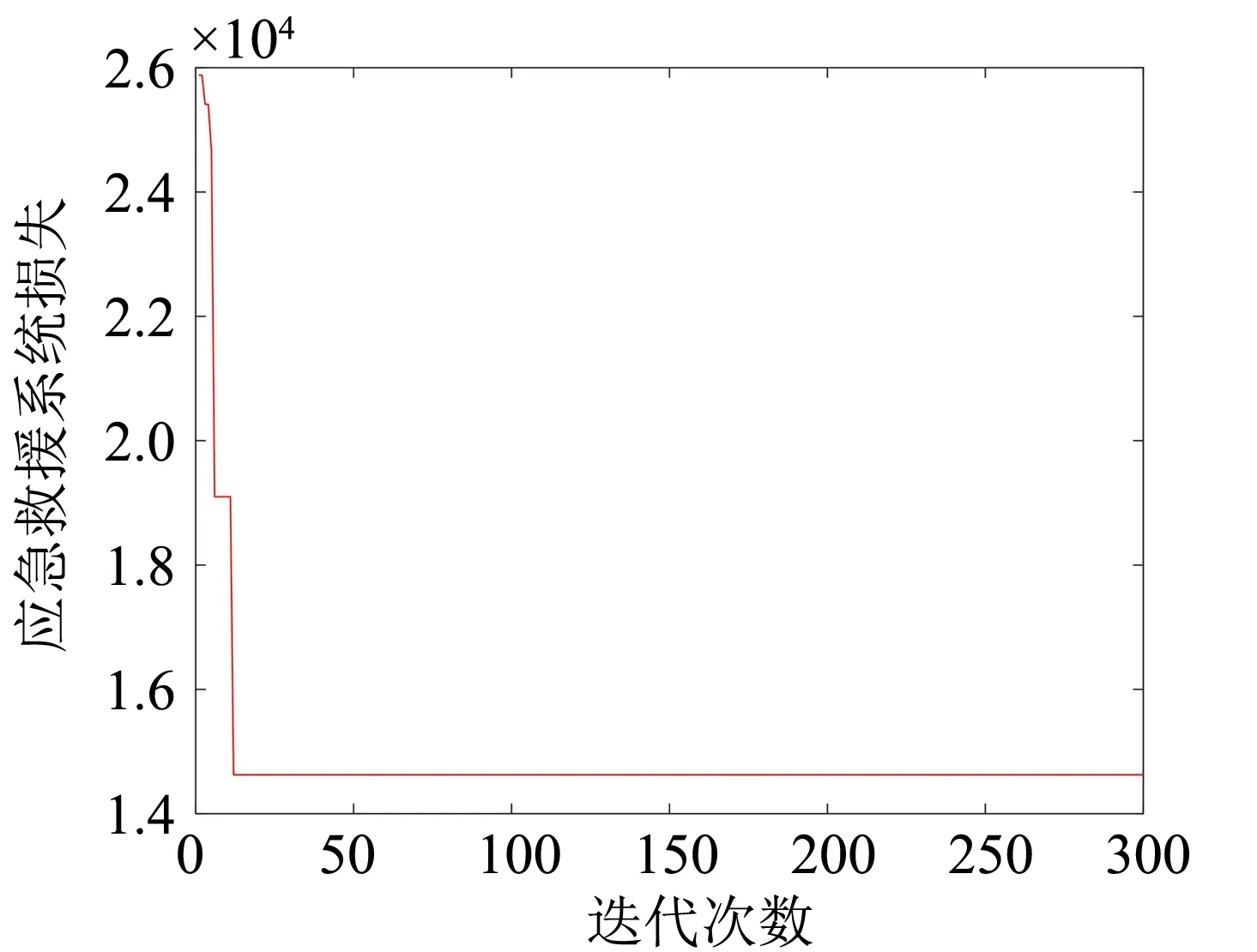
图5 目标2迭代

由算例结果可知本文使用的优化算法得到一个非劣解集，其中的每一个解都代表着一个运输方案，选择带权重的Topsis法对解集进行评价选择。对案例所处背景进行分析：当下属于疫情的中后期，疫情的发展得到控制，物资较为充足各定点医院的需求都可以得到满足，可以优先满足优先级较高的定点医院，对配送的时间方面可以有所放松，则应选取重要程度偏向于应急救援系统损失的配送方案。判断矩阵选取(1,1.5)，权重值为(0.4,0.6)。通过计算每个解到正理想解和到负理想解的距离，选取评价指标值最高的解作为本案例的解，计算为Pareto解中的第6个解，所有车辆的总行驶时间为8.6942小时。其配送方案如表8、图6所示。

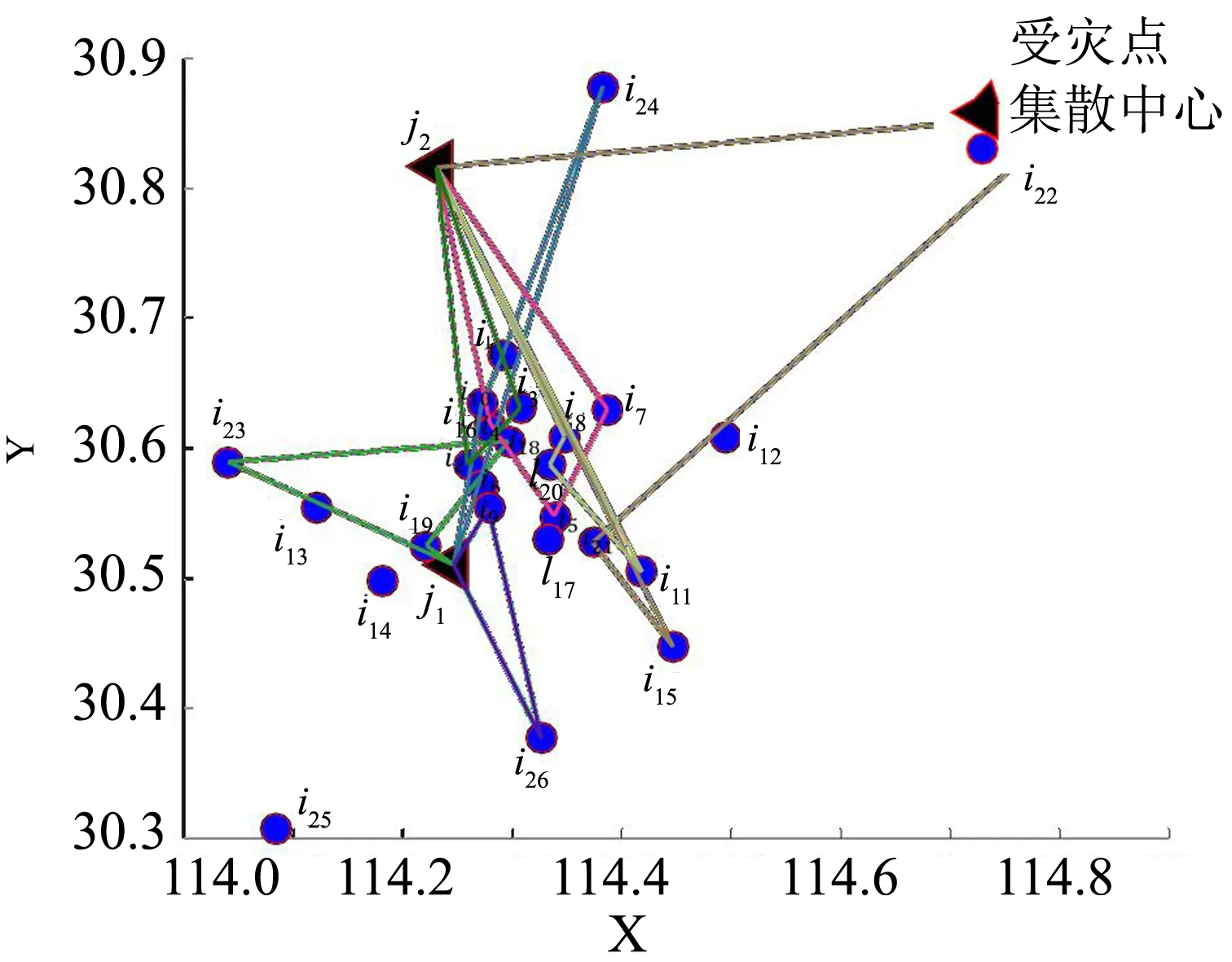
图6 配送路线

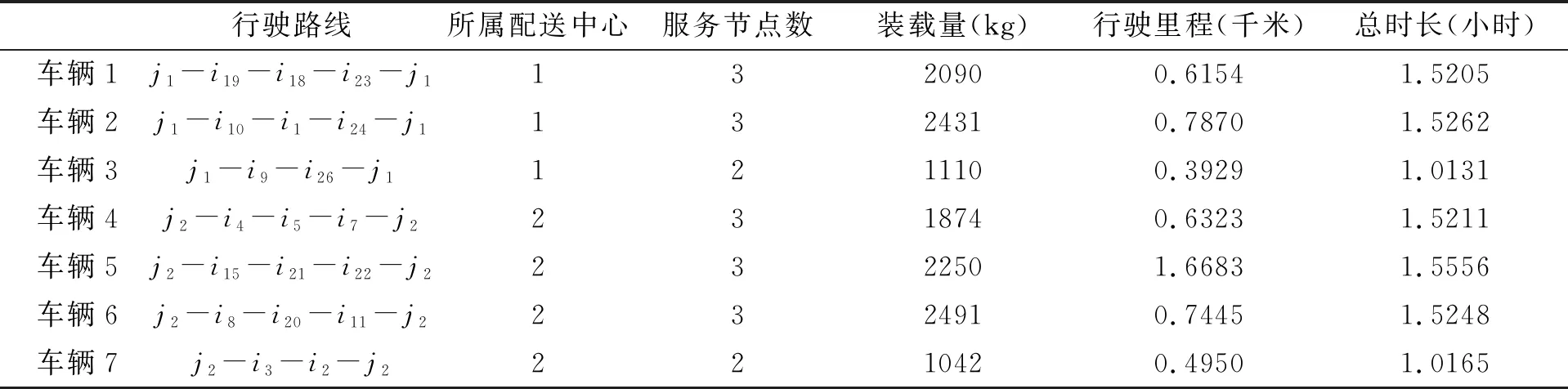
表8 配送方案

五、结论

突发重大疫情时，为了控制疫情发展、支援疫区抗疫工作，需要政府快速响应，组织有效的应急物流活动。本文考虑到疫情发生的突发性、急迫性以及需求不确定性，建立了以配送时间最短和应急物流系统损失最小为目标的应急物资配送模型，模型可根据疫情不同阶段调整参数、选取Pareto解，使之更加贴合实际情况。主要工作结论如下：

(1)突发疫情发生后可根据改进的传染病动力学模型对不确定的需求情况作出预测，该方法相较于其他需求不确定处理方法更加科学，误差较小。

(2)考虑到各疫区疫情严重程度不同的情况，同时考虑不确定需求以及优先级建立多目标应急物资配送模型，并用案例验证了模型的可行性。

(3)设计NSGA-II算法求解模型，得到Pareto解集，并使用Topsis法与AHP方法对求得的Pareto解集进行分析选取最适合案例背景的解，得到最优路线。

通过提前预测应急物资需求并依据优先级及时配送应急物资，实施更加精准、科学、高效的应急物资调度配送策略，对于做好疫情防控有着重大的意义。