大跨人行悬索桥非线性斜风静力稳定研究

管青海王剑李加武刘健新

(1.山东建筑大学交通工程学院，山东济南250101；2.长安大学陕西省公路桥梁与隧道重点实验室，陕西西安710064； 3.天津城建大学 天津市土木建筑结构防护与加固重点实验室，天津300384；4.长安大学 风洞实验室，陕西西安710064)

0 引言

风对桥梁的作用一般简化为静力作用和动力作用两类。 其中，动力作用考虑风与桥梁的能量交换过程，而静力作用只关注静风压力作用，静力作用与动力作用一样，都可能引起桥梁风致失稳。 桥梁静风失稳试验现象最早可追溯到1967 年加拿大Hirai教授的风洞试验。 对于大跨桥梁静风稳定性问题，许多学者[1-7]展开了不断的研究，基本分析了静风失稳发展过程及作用机理。 近年来，又进一步丰富了桥梁静风稳定问题的研究，诸如大跨度斜拉桥静风稳定安全系数的估算方法[8]、基于应变能和动力特性分析了三塔悬索桥气动失稳模式和破坏机理[9]、不同箱梁形式对双主跨斜拉桥静风失稳与颤振发散的竞争关系[10]、非均匀风场(非均匀风速、非均匀风攻角)对大跨度斜拉桥静风稳定性的影响等研究[11-13]。

桥梁实际风场风向可能多变，法向风也不一定是最不利风荷载，已有研究表明大跨桥梁静风失稳最不利状态有可能是小偏角斜风工况[14]。 桥梁斜风静力荷载可以通过风洞试验直接获得斜风作用下的桥梁静气动力系数[15-17]，这种方法的实验装置复杂；还可以基于计算流体动力学计算不同风偏角下的桥梁三分力系数[18]，其计算精度有待提高。 在小风偏角情况下，忽略斜风姿态相对桥梁断面带来的气动外形的影响，斜风正交分解具有一定的工程精度。 文章基于正交分解方法并计入桥梁三维空间变形的影响，不需试验获取斜风静气动力系数，直接推导出桥梁斜风非线性静力荷载计算公式， 研究了420 m主跨人行悬索桥非线性斜风静力稳定。

1 考虑桥梁三维变形的斜风非线性静力荷载

静风荷载与结构变形存在气动耦合作用，使得静风荷载存在荷载非线性，正确给出静风荷载表达式，必须要计入桥梁空间变形的影响。 对于法向风而言，一般只需要计入主梁扭转变形对有效风攻角的影响，而对于斜风作用，则要综合考虑主梁的侧弯、竖弯与扭转等3 方向的空间变形。

设主梁任意i节点作用斜风风速V，主梁i节点发生静风三维空间变形，其中侧弯位移会影响初始风偏角从而形成有效风偏角，扭转角位移会影响初始风攻角从而形成有效风攻角，竖弯位移则影响斜风作用在主梁水平方向的摩擦力。

1.1 有效风偏角与有效风攻角

在静风作用下，主梁发生侧弯变形，相对于主梁初始法线会产生侧弯角，侧弯角叠加初始风偏角为主梁在此级风速下的有效风偏角。 主梁i节点侧弯角φ i( )由式(1)表示为

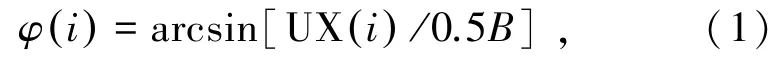
式中φ i( )为主梁i节点侧弯角，rad；UX(i)为主梁i节点背风侧边缘顺向位移，m；B为主梁宽度，m。

进而，当前风速下主梁i节点的有效风偏角βe由式(2)表示为

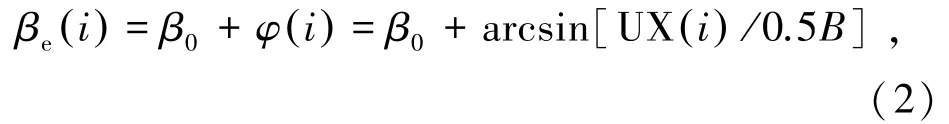
式中βei( )为主梁i节点有效风偏角，rad；β0为初始风偏角，rad。

斜风风攻角来自于斜风法向分量风攻角，在风速作用下，斜风法向分量风攻角并不等于初始风攻角，还要受到有效风偏角的影响，一般而言，斜风法向分量风攻角要大于初始风攻角。 斜风法向分量风攻角由斜风竖平面分量Vsinα0和斜风法平面分量的余弦分量Vcosα0cosβei( )[ ]构成，由式(3)表示为

式中α′ i( ) 为主梁i节点斜风法向分量风攻角，rad；α0为初始风攻角，rad。

有效风攻角角度关系如图1 所示，斜风法向分量风攻角α′ i( ) 叠加主梁扭转角ROTXi( ) ，即为斜风作用下主梁i节点的有效风攻角αe(i)由式(4)表示为

图1 主梁有效风攻角示意图

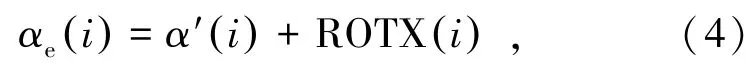
式中αe(i)为主梁i节点有效风攻角，rad；ROTX(i)为主梁i节点扭转角，rad。

1.2 斜风非线性静力荷载表达式

不计桥梁纵坡影响相邻主梁节点的初始高差，主梁i节点的竖弯角由式(5)表示为

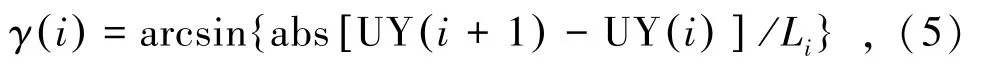
式中γ i( )为主梁i节点竖弯角，rad；UY(i)为主梁i节点的竖向位移，m；Li为主梁i与i+1 节点间的长度，m。

主梁竖向位移作用下， 斜风水平分量Vcosα0sinβei( )[ ]又产生余弦分量和正弦分量，由于有效风偏角βei( ) 和主梁竖弯角γ i( ) 一般较小，其正弦分量Vcosα0sinβei( )[ ]sinγ i( )[ ]也较小，可忽略不计。 斜风最后分解风速为

式中FD(i)、FL(i) 分别为主梁i节点法向风的单位长度静气动阻力、静气动升力，N/m；FM(i) 为主梁i节点法向风的单位长度静气动升力矩，N；CDαei( )[ ]、CLαei( )[ ]、CMαei( )[ ]分别为主梁i节点有效风攻角下的阻力系数、升力系数和升力矩系数，单位量纲为1；cf是与桥面光滑情况相关的摩擦系数，建议根据JTG/T 3360-01—2018《公路桥梁抗风设计规范》偏安全地取最大值0.04[19]；V为斜风风速，m/s；s为主梁周长，m；H为主梁梁高，m；ρ为空气密度，kg/m3。

2 非线性斜风静力稳定理论及数值计算

2.1 非线性斜风静力稳定理论

材料非线性、几何非线性和静风荷载非线性等3 方面是桥梁结构静风稳定分析的非线性问题。 钢桥临界静风失稳前的材料非线性问题不突出，所以材料非线性问题基本可不考虑。 几何非线性问题需要通过迭代几何大变形修正刚度矩阵来实现。 由桥梁位移与风荷载气动耦合引起的静风荷载非线性是分析中最核心的非线性问题，对于常规法向风，静风荷载仅是有效风攻角的函数，斜风静力荷载表达式(6)～(9)知，斜风静力荷载不仅是有效风攻角的函数，同时也是有效风偏角的函数，这就要求在斜风静力荷载迭代计算过程中，不但要求对有效风攻角进行迭代，也要求对有效风偏角同步进行迭代。

大跨桥梁静风失稳问题，即是求解静风荷载几何大变形下的非线性问题，由式(10)表示为

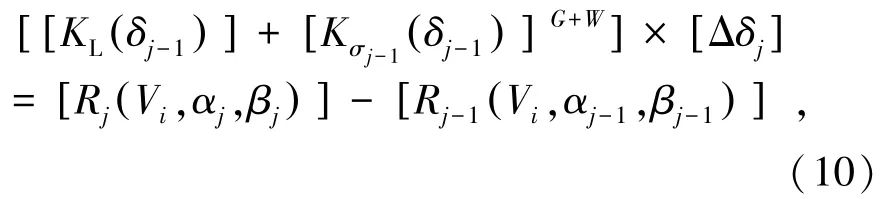
式中左端项[KL(δj-1)]、[Kσj-1(δj-1)]G+W分别为第j-1 迭代步的线弹性刚度矩阵、重力和静风荷载同步叠加作用下的几何刚度矩阵，其中 [ Δδj]为第j步迭代结构位移增量矩阵； 方程右端项[Rj(Vi，αj，βj)]、[Rj-1(Vi，αj-1，βj-1)]为斜风风速Vi作用下有效风攻角αj和有效风偏角βj第j迭代步、有效风攻角αj-1和有效风偏角βj-1第j-1 迭代步的斜风静力荷载，具体计算分别参见式(6)～(9)。

非主梁结构一般不需要计入斜风水平分量风荷载，只需要考虑静风阻力作用，非零风攻角工况下，将静风阻力正交分解为法向力和竖向力。

2.2 基于ANSYS 的斜风静力稳定分析方法

对不同风速下的非线性静风响应计算，需要采用增量法求解方程式(10)。 首先方程式本身需要迭代计算；其次需要对风速分级逐步增量迭代计算，所以实现非线性静风稳定全过程分析要选取内外增量双层迭代范式。

采用有限元软件ANSYS 参数化设计语言APDL 编制计算分析程序。 风攻角正负取决于风荷载方向和结构扭转位移方向，设风荷载方向取ANSYS 总体坐标系正方向，根据右手螺旋法则，正向风攻角定义为使结构产生逆时针扭转位移趋势的来流风向。 具体分析步骤为

(1) 初始自重状态求解，在后续风荷载计算中计入自重应力效应；

(2) 根据主梁空间位移得到斜风工况下的有效风攻角和有效风偏角，计算斜风静力荷载；

(3) 启用应力刚化，采用NEWTON-RAPSON方法(牛顿-拉弗森迭代)计算该级风速下的非线性响应；

(4) 判断求解计算敛散性，若发散，则缩短风速步长，返回步骤(2)重新计算，若收敛，则将斜风法向分量风攻角叠加主梁扭转角得到有效风攻角；

(5) 判定静风荷载敛散性，判定规则为位移范数或静气动力系数范数在规定次数内是否收敛于0，若收敛，则增加风速进行下一级风速计算，如发散，则前一级风速为静风失稳临界风速。一般临近失稳风速时，需缩短风速增量，以求得满足风速精度的临界失稳风速。

3 非线性斜风静力稳定分析

3.1 桥梁概况及有限元模型

3.1.1 桥梁概况

420 m 主跨人行悬索桥位于山东临沂天蒙景区内，大桥横跨V 形山谷，最大纵深达143 m，风环境恶劣，风攻角风偏角常年多变。 施工图设计采用跨径组合为(38+420+47.5)m 双塔悬索桥。 主缆采用预制平行钢丝索股法施工，吊杆间距为3 m，抗风拉索间距为6 m；主梁两侧各设置倾角为35°～53°连续变化抗风缆，出于地形地质条件限制，主梁两侧抗风缆锚固点并不是严格对称；桥塔为门式混凝土结构。

主梁为纵横型钢梁混凝土桥面板结构，主梁两端附有风嘴。 为防护行人安全，栏杆总高度为1.75 m，栏杆立柱附设透风率70%的钢网，主梁全宽4.0 m，宽跨比为1∶105，该桥属于宽跨比很小的窄桥，主梁标准横断面如图2 所示。

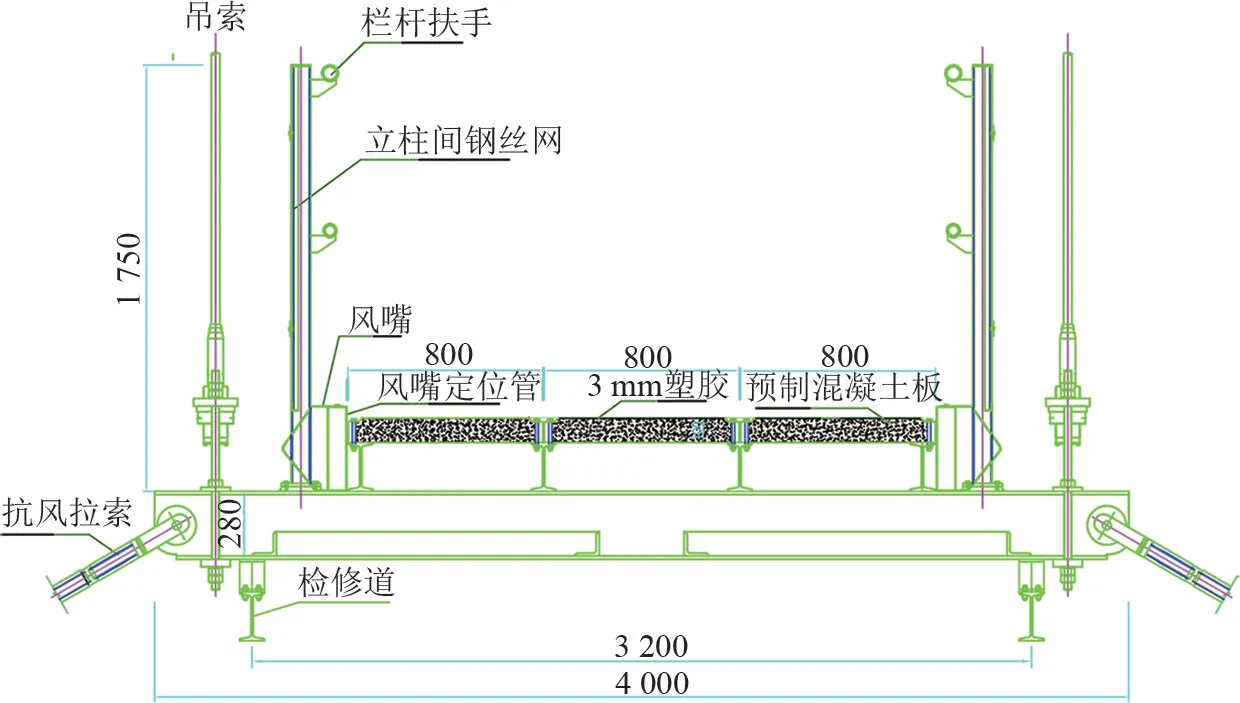
图2 主梁标准横断面图/mm

3.1.2 全桥有限元分析模型

依据大桥结构参数，基于ANSYS 有限元软件建立全桥三维有限元模型。 梁构件采用BEAM4 单元模拟，缆索构件采用LINK10 单元模拟，附属构件、二期铺装等质量构件采用MASS21 单元模拟。 全桥空间有限元模型如图3 所示，大桥刚度低，基频仅为0.24 Hz，主梁扭弯频率比为1.95。

图3 全桥三维有限元模型图

3.2 斜风作用下非线性静风稳定分析

3.2.1 主梁静三分力系数

对于大跨柔性窄悬索桥来讲，高风速下静风扭转位移较大。 常规抗风试验风攻角±10°测试范围可能难以满足静风稳定分析需要，所以文章选取±15°试验风攻角静三分力系数，测定风攻角变化步长取1°，在1°范围内三分力系数取相邻攻角间线性内插值。

在长安大学CA-1 风洞实验室中进行主梁静气动力系数测定试验。 刚体节段试验模型几何缩尺比为1∶14，其模型长度为866 mm、高度为170 mm、宽度为286 mm，模型制作误差≤1 mm。 在试验模型两端设置椭圆形二元板来保证试验模型端部二维绕流特性，试验来流风速为均匀风场15 m/s。 大桥主梁断面±15°风攻角范围内的静三分力系数如图4 所示。

图4 主梁静三分力系数图

3.2.2 法向风作用下的静风失稳发展过程

采用文章提出的分析方法进行了0°风攻角法向风(即0°风偏角)来流作用下的静风稳定性分析，考虑静阵风系数影响，大桥计算静风失稳临界风速为75 m/s。 图5 给出了法向风作用下全跨主梁静风位移随风速的变化过程，受不对称抗风缆的影响，大桥静风位移表现出轻微不对称性；随着静风风速的增长，主梁静风位移增速先慢后快，接近静风失稳临界风速时，增速最大，呈现出明显的静风位移非线性增长特性；最大静风位移基本都发生于主跨跨中位置；静风失稳临界形态时，主梁扭转变形占比较大，竖向位移次之，呈现出一种复杂弯扭耦合的三维空间变形状态。

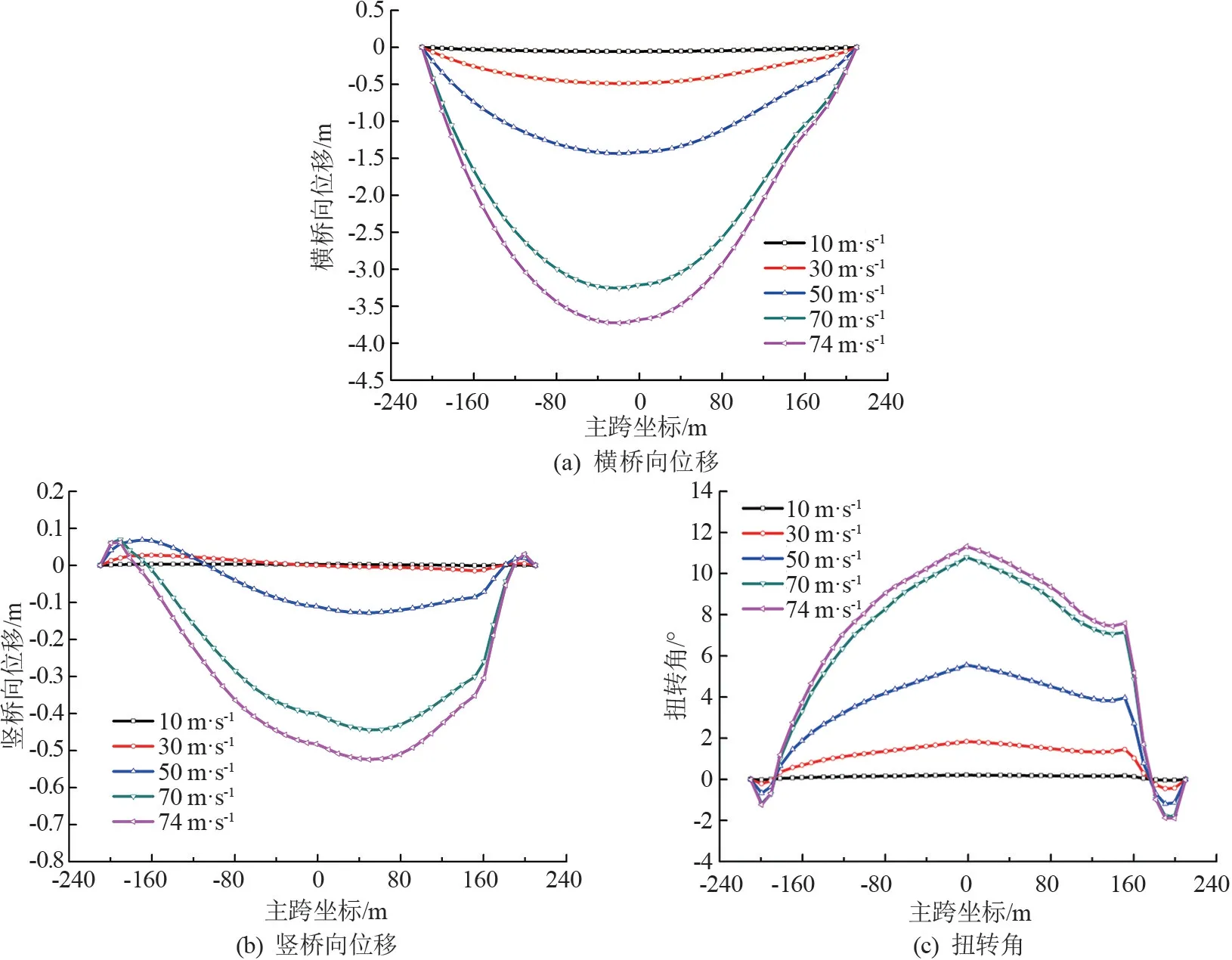
图5 主梁静风位移图

缆索系统的重力刚度是悬索桥的主要刚度来源，一旦缆索构件发生应力松弛，悬索桥系统刚度则迅速衰减，所以缆索构件应力松弛是静风失稳发生的先决条件。 从前述分析可知，大桥静风最大位移发生在跨中位置，所以分析跨中缆索构件的静风应力变化可以基本解释静风失稳的衍变过程。 经计算分析得知，迎风侧缆索构件与背风侧缆索构件静风应力变化呈现明显的不同，迎风侧缆索构件应力随风速的增长而增长，其中迎风侧抗风缆增长幅度最大，临界风速时静风应力增幅高达170%，这也表明抗风缆对静风稳定有较大的贡献；背风侧缆索构件静风应力变化较为复杂，主缆和吊杆应力随风速增长先降后升，而抗风缆和抗风拉索则一直随风速增长而降低，临界风速时，背风侧抗风拉索应力降幅达87%，背风侧抗风缆应力降幅高达98%，基本上背风侧抗风缆接近完全松弛，此时悬索桥残余刚度已不足以抵抗微小的风速增量，所以大桥静风失稳是由抗风缆应力松弛卸载导致的。 跨中主缆与抗风缆应力随风速变化的全过程如图6 所示。

图6 跨中主缆与抗风缆静风应力变化图

3.2.3 斜风作用下静风失稳临界风速

考察斜风对大跨度人行悬索桥静风稳定性的影响，采用提出的分析方法计算了0°、+3°、-3°、+5°、-5°等风攻角下0°、5°、10°、15°、和20°风偏角的大桥静风失稳临界风速，计算结果如图7 所示。

图7 静风失稳临界风速图

由计算结果可知，负攻角对大桥静风稳定有利，正攻角静风失稳临界风速远低于负攻角，最低静风失稳临界风速发生在0°初始风偏角，随着风偏角的增大，静风失稳临界风速随之增大，小角度斜风对该桥静风失稳临界风速影响不大。 在一定程度上，斜风降低了法向作用分量，但是同时增加了水平分量，其作用对于桥梁静风稳定的影响利弊不一，应该因桥而异。 一般来说，如果增加的水平分量作用不足以补偿降低的法向分量作用，则最不利静风工况总是来自于法向风，反之则来自于斜风。

4 结论

文章提出了一种实用的斜风作用下大跨桥梁静风稳定性分析方法，其可以计入桥梁静风空间变形对斜风静力荷载的影响，推导了斜风荷载理论表达式，基于所提出的方法编制了内外两重迭代的大跨桥梁斜风静力稳定分析程序，研究了420 m 主跨人行悬索桥斜风静力失稳发展过程，分析了风偏角对该类桥梁静风失稳临界风速的影响，主要得出以下结论:

(1) 斜风静力荷载表达式是有效风攻角与有效风偏角的函数，精确考虑斜风静力荷载作用，要求对有效风攻角和有效风偏角同步进行迭代。 基于正交分解方法推导斜风静力荷载表达式的假设前提为:在小偏角下，忽略桥梁断面相对于斜风姿态带来的气动外形影响。 所以只有小偏角斜风才可以应用文章所推导的斜风静力荷载理论公式。

(2) 低风速下主梁静风位移增长相对缓慢，高风速下主梁位移非线性迅速增大，静风失稳形态以主梁扭转变形为主，同时竖向位移分量也占有较大比例，是一种复杂的弯曲扭转耦合的三维空间变形状态。 在静风弯扭空间大变形作用下，背风侧缆索系统应力大幅卸载，最终背风侧抗风缆应力接近完全卸载导致悬索桥整个系统刚度丧失，从而发生了静风失稳。

(3) 以往某些大跨度公路桥梁静风失稳最不利工况来自小偏角斜风，而文章分析的大跨度人行悬索桥最不利静风失稳来自于法向风，小角度斜风对该桥静风失稳临界风速影响不大。 对于其他类型的桥梁，该结论有待进一步检验。