关于序γ αβ-理想统计收敛的模糊数列空间
2022-08-18冯雪
冯 雪
(青海民族大学 数学与统计学院, 西宁 810007)
1965年,美国加州大学控制论专家Zadeh[1]初次提出了模糊集的概念,发表题为《模糊集合论》的文章,此篇论文的发表,标志着模糊数学这门学科的诞生.同时,在“模糊集合”上逐步建立运算、变换规律,开始了模糊数学理论的研究.日常生活中,我们要解决的实际问题常常含有一些不确定性,而模糊数学理论[2]能够为处理看起来相当复杂的模糊系统提供数学方法,模糊数列收敛问题是模糊数学理论的重要在组成部分,根据解决实际问题的需要,学者们相继提出并讨论了有关模糊数列的各种收敛问题.在文献[3]中,Savas[3]给出了模糊数列统计收敛的一个新的定义,并且将模糊数列的统计收敛用自然密度为零的模糊数列和普通收敛的模糊数列来表示出来.2006年,Aytar等[4]给出了有界的模糊数列统计收敛时,它的统计上极限和统计下极限,并且证明了统计上、下极限与有界的模糊数列统计收敛之间的关系.2008年,Kumar[5]将模糊数列统计收敛作以推广,引入了模糊数列理想收敛的定义.2012年,巩增泰等人[6]定义了模糊数列理想统计收敛和理想缺项统计收敛,并且证明了如果模糊数列x={xk}统计收敛,则它一定理想统计收敛;如果模糊数列x={xk}缺项统计收敛,则它一定理想缺项统计收敛.Orlicz序列空间是lp(1≤p<∞)空间的推广,由Lindenstrauss等人[7]最早提出,并且得到任意一个Orlicz序列空间lM都会包含一个同构于lp(1≤p<∞)的子空间的相关结果.Parashar[8],Tripathy等人[9]在接下来对Orlicz序列空间研究工作中,从Orlicz序列空间的空间性质、推广范围以及与其他序列空间的性质比较等方面进行持续研究,进一步加深了Orlicz序列空间理论.我国吴从炘等人[10]自1985年起,开始较为系统地研究Orlicz空间理论.2015年,巩增泰、冯雪[11]引入了模糊数序列关于序γαβ-统计收敛和关于序γ强αβ-收敛的概念.同时,建立了关于序γαβ-统计收敛和关于序γ强αβ-收敛的模糊数列空间的一些联系.得到结论,如果一个模糊数列是关于序γ强αβ-收敛的,那么它是关于序γαβ-统计收敛的.
本文旨在扩大了模糊数列收敛范围,以非降正数列为a(n)、β(n)框架,将模糊数列统计收敛和强收敛置于理想意义下,定义了两种新的模糊数列收敛的概念——关于序γαβ-理想统计收敛和关于序γ强αβ-理想收敛.同时,证明了这两种收敛的模糊数列空间的性质,以及这两种收敛之间的相互关系.给定模糊数列x={xk},若它是强αβ-收敛的模糊数列,则x={xk}一定是αβ-理想统计收敛的;当模糊数列x={xk}有界时,反之成立.
1 定义和说明
定义1.1[1]模糊数u是指实数R上的模糊集,u满足:正规的凸模糊集,隶属函数u(x)是上半连续的,支撑集[u]0=cl{x∈R∶u(x)>0}为紧集,所有模糊数所组成的集合记作E1.对∀r,0≤r≤1,水平截集[u]r={x∶u(x)≥r}是一个闭区间.对u,v∈E1,k∈R加法和数乘定义如下:
[u+v]r=[u]r+[v]r; [ku]r=k[u]r.
模糊数u,v∈E1间的距离定义为

定义1.2[12]设X为非空集合,称I⊂2X为X上的理想,指:
1)φ∈I;
2)若A,B∈I,则A∪B∈I;
3)对A∈I,若B⊂A,则B∈I.
需要注意,如果I≠φ且X∉I则I称为X的非平凡理想.本文没有特别标注的情况下,理想I是自然数集N的非平凡理想.
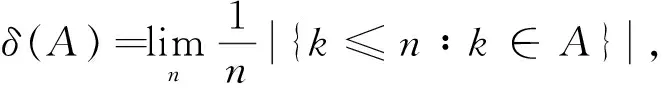
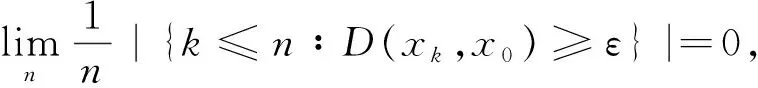
定义1.5[5]模糊数列x={xk}理想收敛于模糊数l,指对任给的ε>0,集合A(ε)={k≤n∶D(xk,l)≥ε}∈I,其中:I为N的非平凡理想.
定义1.6[11]设α(n)和β(n)是正数列,满足下列条件:
1)α(n)和β(n)都是非降数列;
2)β(n)≥α(n);
3)β(n)-α(n)→∞,当n→∞.
记∧为满足上述三个条件的(α,β)对.

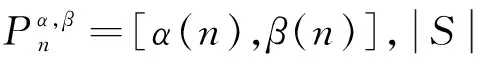
推论1.1[11]设K和M是N的两个子集,0 1)δα,β(φ,r)=0; 2)δα,β(N,1)=1; 3)若K是有限集,则δα,β(K,r)=0; 4)若K⊂M,则δα,β(K,r)≤δα,β(M,r); 5)δα,β(K,δ)≤δα,β(K,r). 定理2.1 设x={xk},y={yk}是模糊数列: 证明: 1)当c=0时,结论显然成立. 假设c≠0,那么 所以有 因为 D(xk+yk,x0+y0)≤D(xk+yk,x0+yk)+D(x0+yk,x0+y0)=D(xk+x0)+D(yk,y0) 又∀ε>0,有 所以,可得 定理2.2 设x={xk}是模糊数列,那么存在αβ-理想统计收敛的模糊数列y={yk},使得对几乎所有的k都有xk=yk成立,则x=(xk)也是αβ-理想统计收敛的数列. 本文针对我院2016年1月-2017年7月收集的使用丁溴东莨菪碱的患者的病例进行归纳分析,旨在掌握丁溴东莨菪碱的使用注意事项,提高用药合理性,减少药源性不良反应的发生。 因为模糊数列x={xk}αβ-理想统计收敛. 证明:设0 定理2.4 设x={kk}是模糊数列,{xk}是关于序γαβ-理想统计收敛的,当且仅当它是关于序γαβ-理想统计柯西列. 那么 可得 所以{x}是αβ-理想统计柯西列. 那么D(xNp,xNq)≤D(xKpq,xNp)+D(xKpq,xNq),所以 因此,{xNp}∶p=1,2,3,…是αβ-理想统计柯西列,设{XNp}收敛于x0,对∀ε>0,εp∶p=1,2,3,…→0,存在p0,使得 那么D(xk,x0)≤D(xk,xNp0)+D(xp0,x0),所以有 所以{xk},αβ-是理想统计收敛的. 定义3.1 关于序强理想收敛的模糊数列定义如下: 根据上面不等式,可得 因此 定义3.2 设p={pk}是正实数列,对任意r∈(0,1],模糊数列x=(xk)称为关于序r强αβ(p)-理想收敛,若对于模糊数列x,有 记 与定理3.1、定理3.2相似模糊数列关于序r强αβ(p)-理想收敛有如下结论. 所以, 证明对给定ε>0,有 所以, 证明 min{εh,εH} 可得 max{Th,TH}+max{Th,TH} 所以 3)由1)和2)显然可得3). 本文以非降正数列a(n)、β(n)为框架,将模糊数列统计收敛和强收敛置于理想意义下,定义了两种新的模糊数列收敛的概念——关于序γαβ-理想统计收敛和关于序γ强αβ-理想收敛.同时,证明了这两种收敛的模糊数列空间的性质,以及这两种收敛之间的相互关系.给定模糊数列x={xk},若它是强αβ-收敛的模糊数列,则x={xk}一定是αβ-理想统计收敛的;当模糊数列x={xk}有界时,反之成立.2 模糊数列关于序γ αβ-理想统计收敛
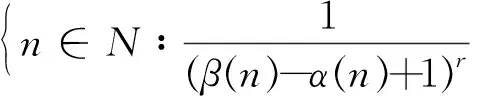

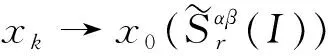
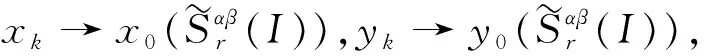

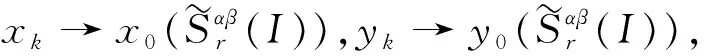

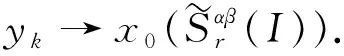

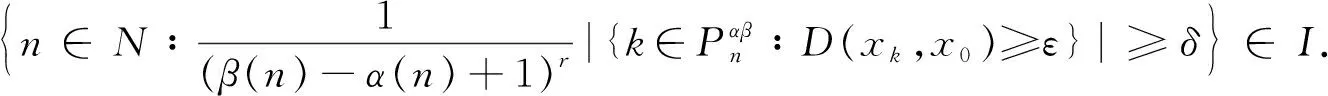



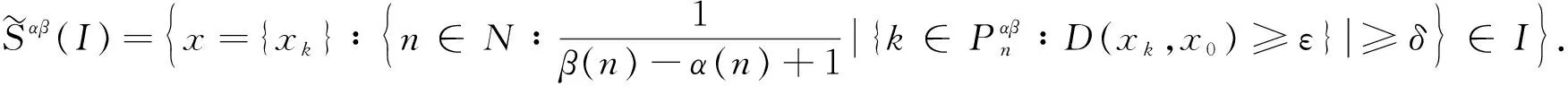
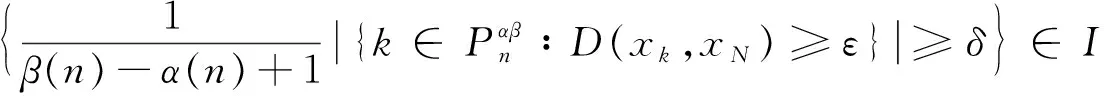

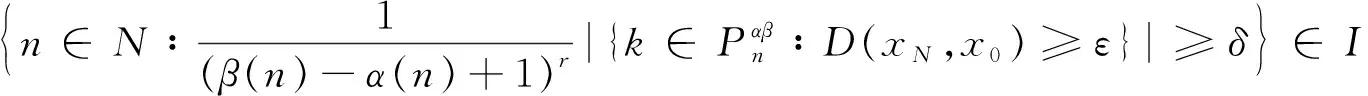
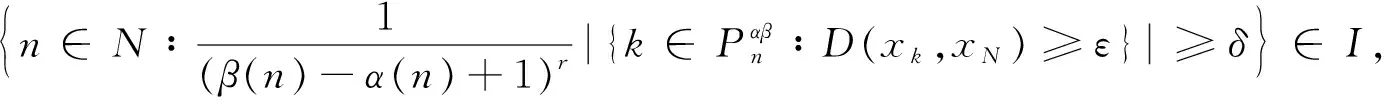
3 模糊数列关于序γ强αβ-理想收敛
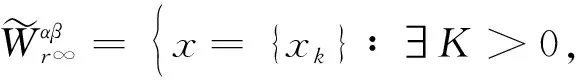


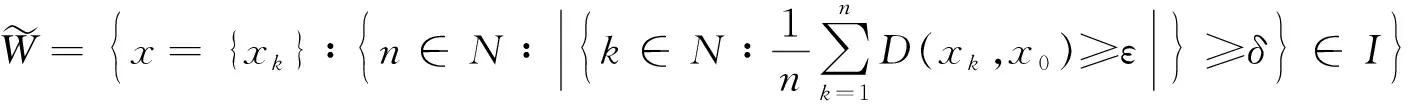

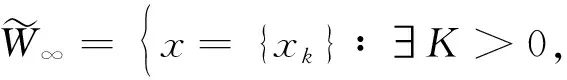
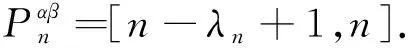







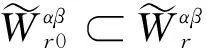
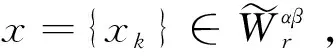

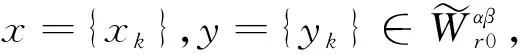


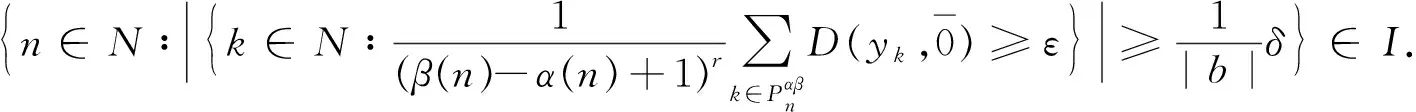




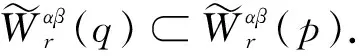
4 模糊数列关于序γ αβ-理想统计收敛与强αβ-理想收敛之间的关系
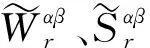
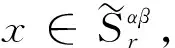


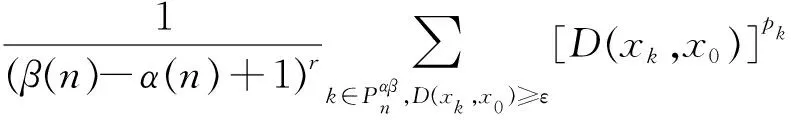


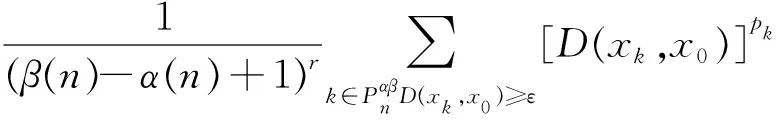

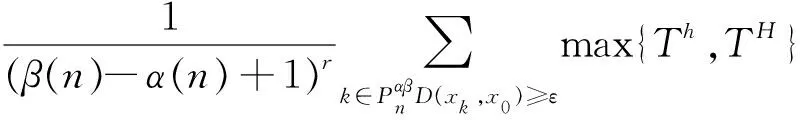
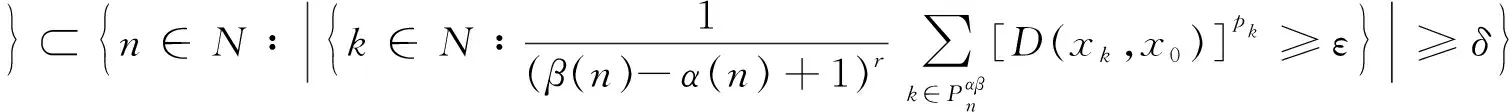
5 结 语
