带切比雪夫多项式的混沌神经网络研究
2022-08-18徐耀群杨振华
徐耀群,杨振华
(1.哈尔滨商业大学 计算机与信息工程学院,哈尔滨 150028; 2.哈尔滨商业大学 系统工程研究所,哈尔滨 150028)
Hopfield首次从动力学系统的角度研究神经网络,开创性的将能量函数的极小解与网络的平衡态进行映射,使得神经网络寻优过程与动力学系统的演化问题相对应,从而极大的推动了神经网络在计算机科学中的应用.但是由于Hopfield神经网络采用梯度下降策略,使得网络在寻优过程中非常容易陷入局部极小解和不可行解,限制了Hopfield神经网路的优化能力.许多学者[1-3]受生物神经元混沌特性的启发,将混沌动力学[4-5]注入Hopfield神经网络中,使得神经网络利用混沌动力学的全局遍历性可以有效地避免网络在寻优过程中陷入局部极小解的问题,提高了网络的优化能力.近年来许多学者为了提高神经网络的优化性能,在网络的激活函数、引入自反馈项和退火策略等方面进行创新研究.其中:Potapove[6]提出网络在非单调递增函数的作用下可以加速进入混沌状态.Shuai[7]等提出神经网络的激活函数可以多样化.何振亚等通过在激励函数中引入暂态混沌和时变增益提出了一种新的混沌神经网络模型.胡志强[8]等提出激活函数由变频正弦函数与Sigmoid函数加权和的形式构成的一种新的混沌神经网络。徐耀群[9]等提出了由Sigmoid函数和连续小波函数加和而成的激励函数,并通过与Gauss函数的比较仿真验证了连续小波函数所具有的优势;叶永刚[10]等提出将较高的非线性度及较好的函数逼近能力的Legendre函数与Sigmoid的线性组合作为新的激励函数,验证了模型的有效性.许楠[11]等提出了将反三函数引入到网络的自反馈项中,提高了网络的优化性能.胡志强[12]等提出了一种通过网路的动态演化过程来自适应地调整网络退火速率的混沌神经网络.
本文利用较高逼近能力的切比雪夫多项式对网络的自反馈权值进行优化,构建了一种新的混沌神经元模型.模型的混沌特性通过最大Lyapunov指数时间演化图和倒分叉图来进行分析.模型的有效性通过旅行商问题和函数优化问题的仿真实验进行验证.
1 带Chebyschev多项式的混沌神经元网络模型
1.1 Chebyschev多项式
切比雪夫多项式[13]来源于多倍角的余弦函数和正弦函数的展开式,是计算数学中的一类特殊函数.第一类切比雪夫多项式是一组正交多项式,是微分方程(1-x2)y″-xy′+n2y=0的解.第一类切比雪夫多项式描述为:
(1)
当n=1,2,3,5时,切比雪夫多项式的图像如图1所示.

图1 T1, T2, T3, T4, T5图像
1.2 单神经元的混沌动力学特性
将切比雪夫多项式引入到神经网络的内部函数中构建的新的混沌神经元模型如下:
x(t)=1/(1+exp(-y(t)/ε0))
(2)
y(t+1)=ky(t)-z(t)f(x(t)-I0)
(3)
(4)
f(u)=cjTi(u),i=0,1,2…
(5)
z(t+1)=(1-β)z(t)
(6)
其中:x(t)是激活函数即神经元在t时刻的输出;I0为正参数;ε0为激活函数的陡度系数;y(t)为神经元在t时刻的内部状态;k取值范围为0≤k≤1,表示神经元保留内部状态的能力;Tn(x)为切比雪夫多项式;f(u)为自反馈权值的优化策略;z(t)是自反馈连接项;β是模拟退火参数.
最大的Lyapunov指数的时间演化图和倒置的分叉图描述神经元的混沌特性.由于混沌运动对初始值条件极为敏感,因此类似初始值产生的两个轨道会随时间推移呈指数级分离.Lyapunov指数是用于定量描述轨道分离的程度.Lyapunov指数的计算公式如下.
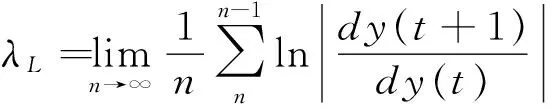
(7)
本文构建的混沌神经元模型中取f(u)=c1T1-c3T3,有:
(8)
(9)
在一维映射中,λL>0显示相邻轨道指数分离,运动轨道各部分不稳定,处于混沌状态,其值的大小表示混沌状态的强度.λL<0表明相邻的轨道运动最终移动更近,相积收缩,运动稳定.λL=0表明该模型处于稳定性和混乱的关键值.
分析混沌神经元的动力学特性,如下设置参数:ε0=0.02,y(1)=0.1,z(1)=0.98,k=1,I0=0.57,β=0.001,c1=1,c2=-0.01.神经元的最大Lyapunov指数时间演化图和倒分叉图如图2~3所示.

图2 c1=1,c2=-0.01时神经元的倒分叉图
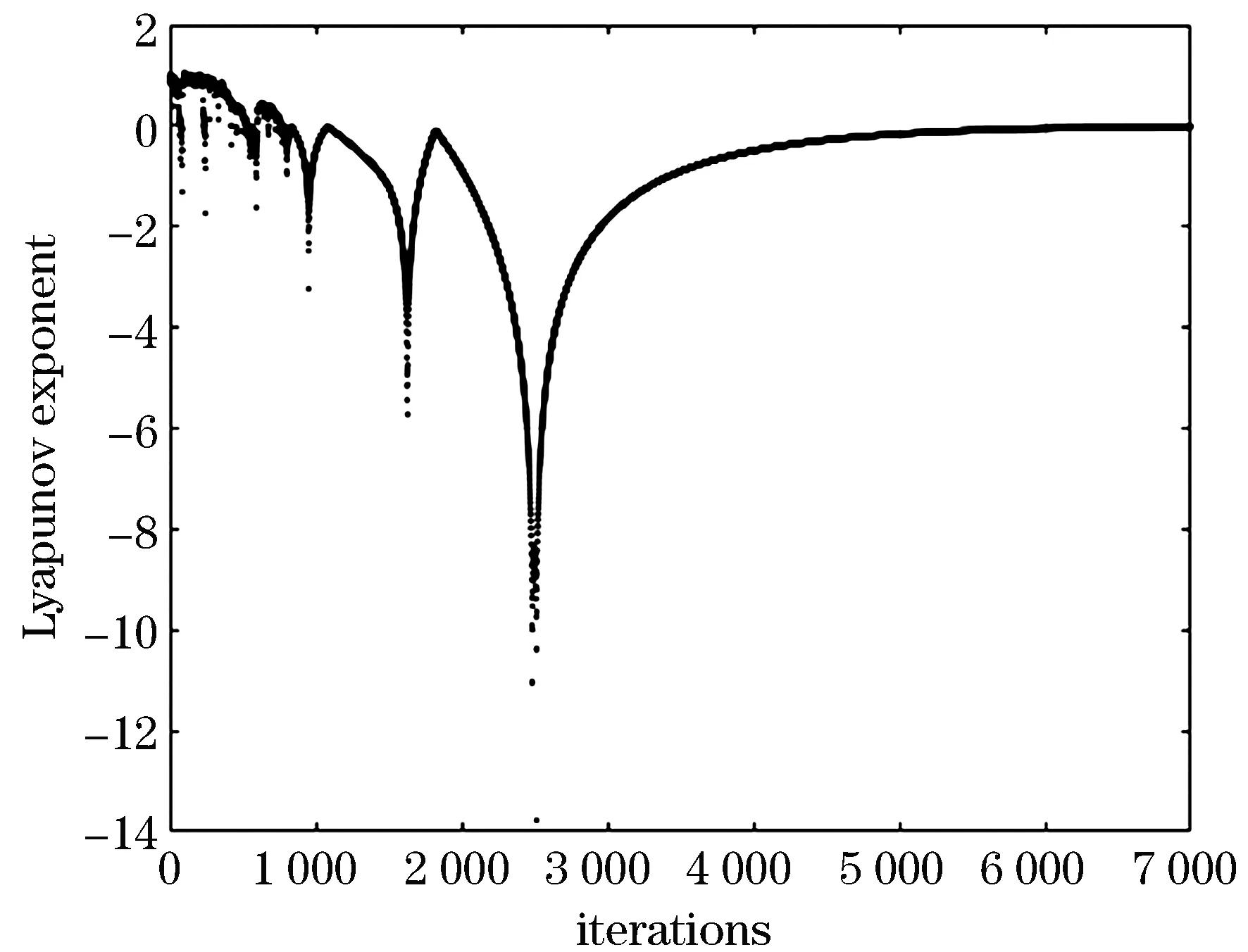
图3 c1=1,c2=-0.01时最大Lyapunov指数时间演化图
为了研究对神经元动力学特性的影响,分别取c1=3,c2=-0.03和c1=10,c2=-0.1.神经元的Lyapunov指数时间演化图和倒分叉图如图4~7所示.
从图2可以看出新构建的单神经元具有混沌特性,图3、4显示c1和c2影响神经元混沌特性,随着c1和c2的增大,神经元混沌特性增强,退出混沌的时间延长.神经元混沌状态持续的时间直接影响网络进行寻优的结果,混沌状态持续时间较短会导致寻优过程由于无法跳出局部极小值而找不到最优解,而混沌状态持续状态过长,会延长寻优过程,降低了算法的效率.因此选择合适的混沌持续时间,可以避免在寻优过程中陷入局部极小值的同时能缩短寻优时间,提高了网络的优化能力.
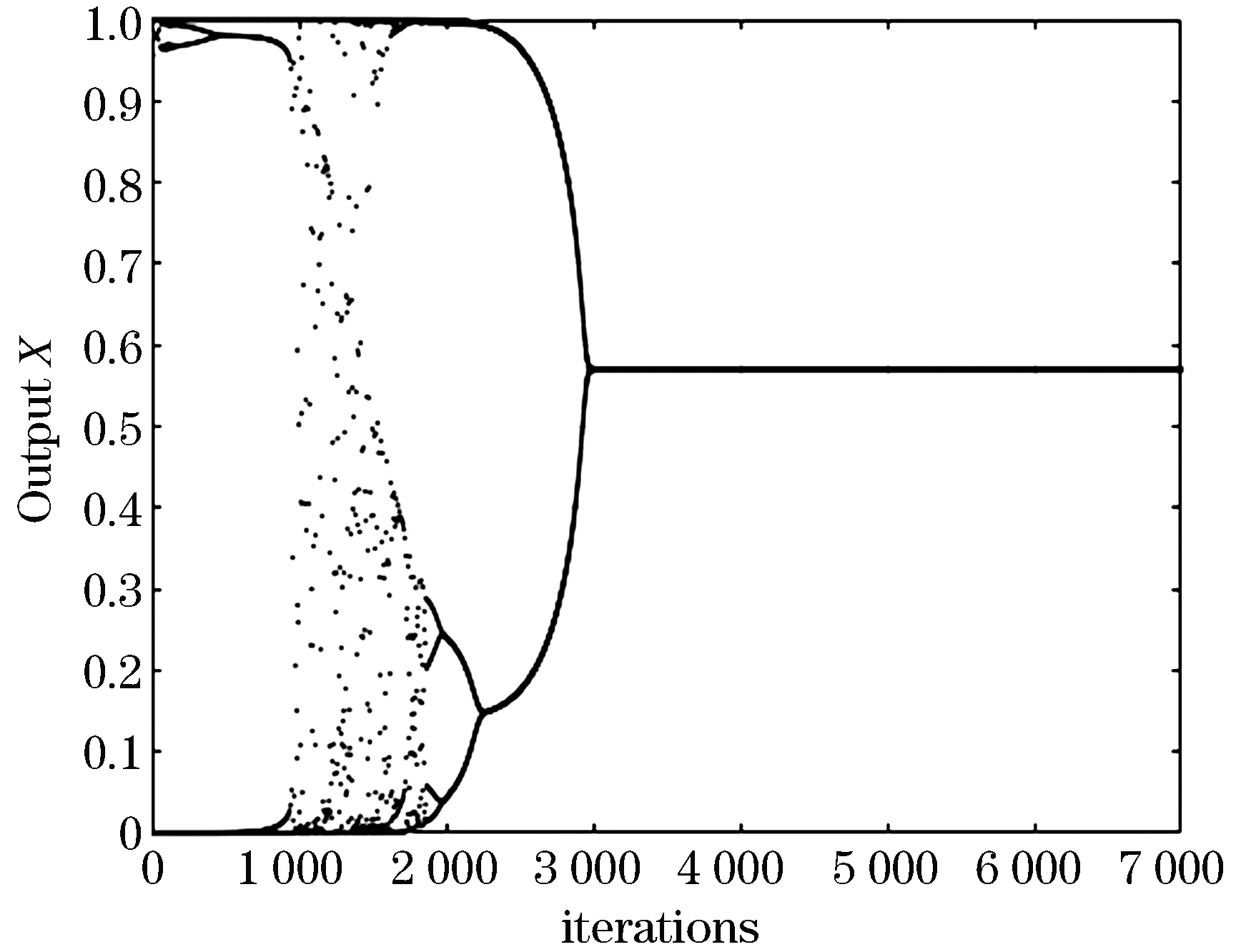
图4 c1=3,c2=-0.03时神经元的倒分叉图

图5 c1=3,c2=-0.03时最大Lyapunov指数时间演化图

图6 c1=10,c2=-0.1时神经元的倒分叉图
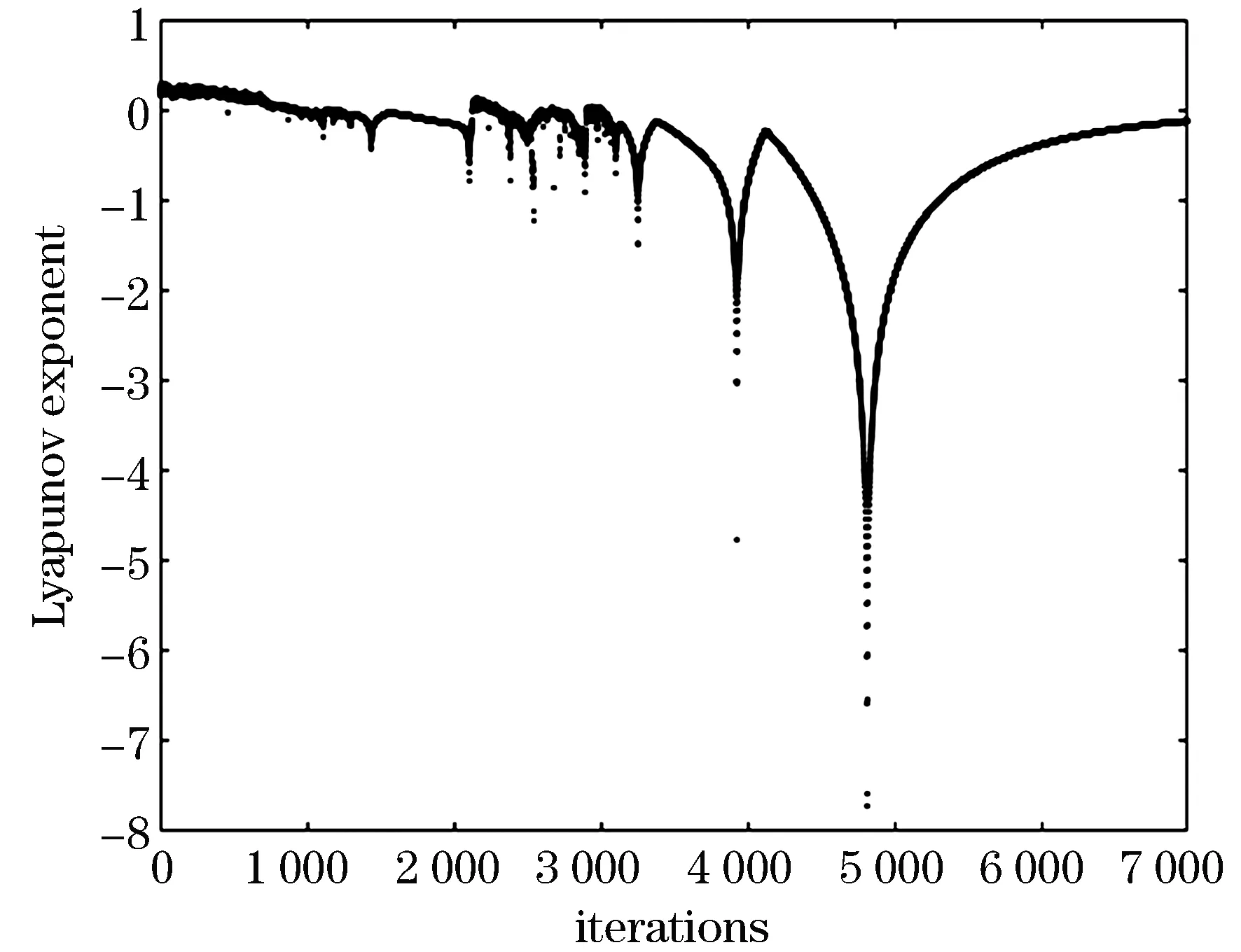
图7 c1=10,c2=-0.1时最大Lyapunov指数时间演化图
1.3 带切比雪夫多项式的暂态混沌神经网络
构建如下暂态混沌神经网络模型:
x(t)=1/(1+exp(-yi(t)/ε0))
(10)
zi(t)f(xi(t)-I0)
(11)
zi(t+1)=(1-β)zi(t)
(12)
(13)
f(u)=cjTi(u),i=0,1,2…
(14)
其中:yi(t)是第i神经元在t时刻的内部状态;xi(t)是激活函数即第i个神经元在t时刻的输出;zi(t)是自反馈连接项;f(u)为自反馈权值的优化策略;Tn(x)为切比雪夫多项式;β是分段模拟退火参数;wij为神经元j和i的权值,其中:wij=wji,wii=0;为激活函数的陡度系数;Ii为神经元i的输入偏差;k为神经隔膜的阻尼因子,0≤k≤1,其反应网络记忆保留或遗忘内部状态的能力;γ为输入的正的尺度参数;I0为一正参数.
2 组合优化问题的应用
2.1 函数优化中的应用
取如下优化函数[14]:
f(x1,x2)=(x1-0.7)2[(x2+0.6)2+0.1]+
(x2-0.5)2[(x1+0.4)2+0.15]
(16)
上述优化函数的最小值为0;最小值点为(0.7,0.5);局部极小值点为(0.6,0.4)与(0.6,0.5)。
取ε0=0.02,k=1,∂=0.05,I0=0.57,β=0.005,y(1)=0.383,y(2)=0.283,z1=z2=0.98,c1=1,c2=-0.01.能量函数的时间演化图如图8所示,神经元输出值和时间演化图如图9所示.
其他参数与上述保持一致,取c1=3,c2=-0.03神经元输出值x1和x2时间演化图如图10所示.

图8 c1=1,c2=-0.01时优化函数的能量函数时间演化图
图9表示,程序在运行700次左右时,网络能找到最小值点.说明构建新的混沌神经网路具有函数优化的能力.为了进一步研究参数c1,c2对网络进行函数优化的影响,取c1=3,c2=-0.03进行仿真实验,结果显示程序运行约1 000次左右,网络退出混沌状态达到平衡状态,找到最小值点.结合图9、10,说明参数c1和c2直接影响网络退出混沌状态的时间,因此在实际应用中,应当选择合适的参数,来提高网络的优化能力.

图9 c1=1,c2=-0.01时神经元输出值x1x2的时间演化图

图10 c1=3,c2=-0.03时神经元输出值x1x2的时间演化图
2.2 10城市旅行商问题应用
在组合优化领域中,TSP[15]问题由于其求解难度较大,很多学者一直在寻找一种高效,符合实际的方法来解决此问题.TSP问题可以简单描述为“寻找一条包含全部n个城市的最短环路,其中:每个城市必须有且只有一次被访问”.(n-1)!/2是n个城市TSP问题可能的路径数.
本文将新构建暂态混沌神经网络模型应用于求解10城市的TSP问题,取能量函数为:
(17)
其中:xij指城市i在顺序j时访问,参数A=B,dik表示城市i与城市k的距离,最短的有效路径等效为一个全局最小的能量值.选取文献5中的归一化后的10城市坐标,如下:
(0.4,0.443 9);(0.243 9,0.146 3);(0.170 7,0.229 3);(0.229 3,0.716);(0.517 1,0.941 4);(0.873 2,0.653 6);(0.687 8,0.521 9);(0.848 8,0.360 9);(0.668 3,0.253 6);(0.619 5,0.263 4);此坐标下满足10城市TSP问题的最短路径为2.677 6,如图11所示.

图11 10城市TSP最优解
在新构建的混沌神经网络模型中,采用切比雪夫多项式对网络的自反馈权值进行优化,即f(u)=cjTi(u),本文研究优化策略中系数c对网络求解旅行商问题的影响.在新的混沌神经网络模型中,取参数A=B=1,D=2.5,∂=1,k=1,I0=0.57,ε0=0.02,z(1)=0.98,β1=0.003,β2=0.004,c1=-100c2,xij的初值在程序每次运行时200次随机在区间(-0.1,0.1)内赋值.
在新构建的混沌神经网络模型中,采用切比雪夫多项式对网络的自反馈权值进行优化,即f(u)=cjTi(u),本文研究优化策略中系数c对网络求解旅行商问题的影响.在新的混沌神经网络模型中,取参数A=B=1,D=2.5,∂=1,k=1,I0=0.57,ε0=0.02,z(1)=0.98,β1=0.003,β2=0.004,c1=-100c2,xij的初值在程序每次运行时200次随机在区间(-0.1,0.1)内赋值.
仿真结果如表1所示,结果表明此模型在上述参数的设置下求解10城市TSP问题性能较高.
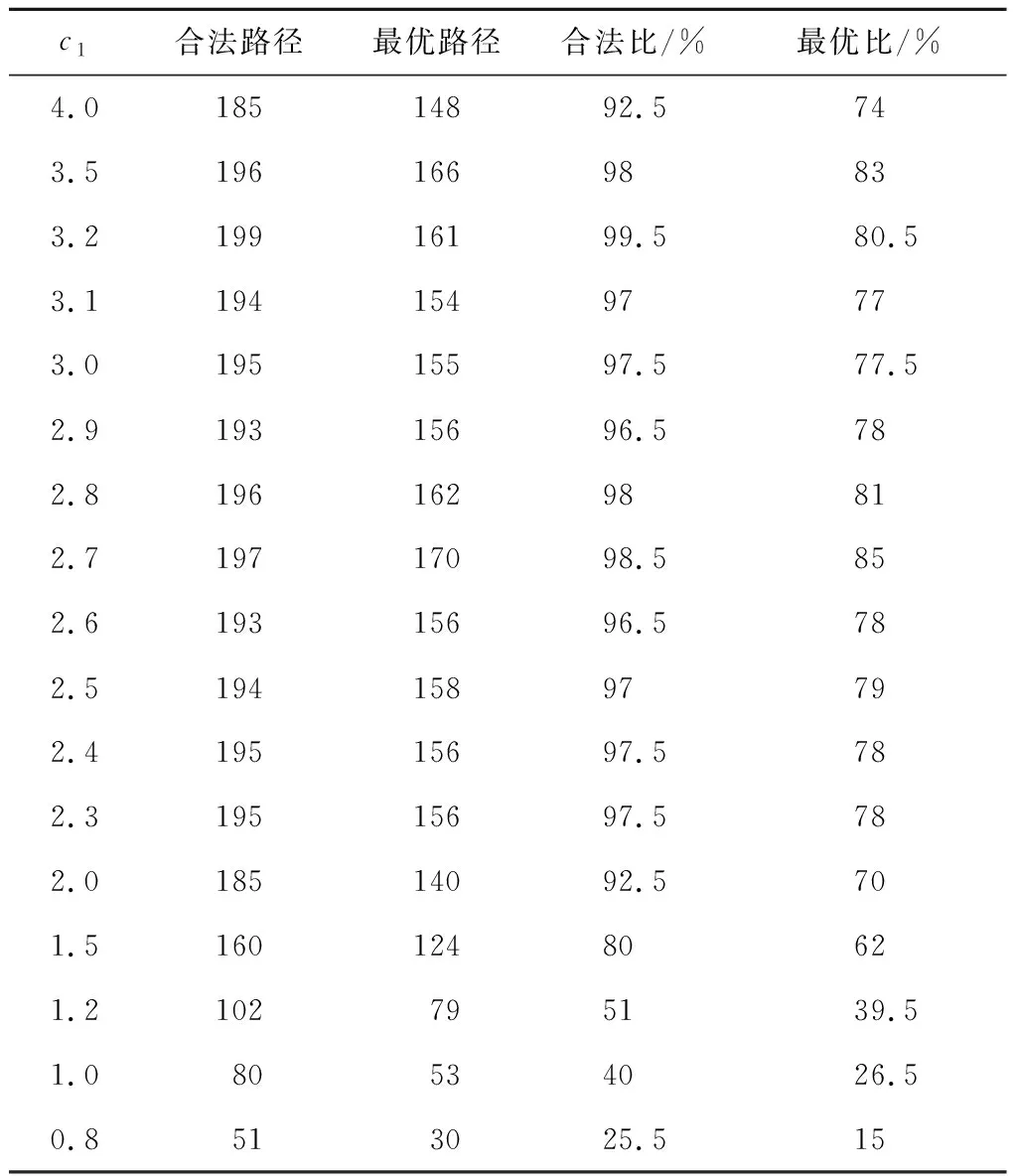
表1 求解10城市旅行商的结果
由表1可以看出,当c1取值小于2.0时,合法路径和最优路径都较小,此时混沌神经网络寻优性能较低.当c1取值大于3.5时,最优路径较小,混沌神经网络不能很稳定地收敛于最优解.当c1取值在2.8附近时,网络求解组合优化问题能力较高.
3 结 语
本文将较高逼近能力的切比雪夫多项式引入到混沌神经网络中,构建了一种新的暂态混沌神经网络模型.模型的混沌动力学特性通过最大Lyapunov指数时间演化图和倒分叉图来进行分析.分析了指定参数对网络混沌特性和网络优化性能的影响.模型的有效性通过旅行商问题和函数优化问题的仿真实验进行验证.通过仿真实验结果显示,新构建的暂态混沌神经网路模型,具有很好的求解组合优化的能力.
