ARIMA-GARCH-M模型在短期股票预测中的应用

熊 政，车文刚

(昆明理工大学 信息工程与自动化学院， 云南 昆明 650500)

股票投资是人们主要的投资手段之一，近年来，越来越多的人开始关注股票市场并加入到股民这一行列。然而，对于股民来说，在面对上千支股票时，选择哪一支股票可以降低亏损风险带来不错的收益就需要一些辅助手段了。金融时间序列模型是股票预测中最常用的方法，也被认为是预测股市变化最好的工具之一，准确的股票预测能够帮助投资者做出正确的判断。而对于个人投资者来说，高速、简易、预测准确的轻量型时间序列模型更加适合个人投资者在日常生活中的应用，也是众多科研工作者研究的目标。

张颖超等[1]通过建立ARIMA模型对股票未来的上证指数进行预测和分析，发现该模型在未来4个交易日里的预测效果较好。刘松等[2]通过建立ARIMA模型对选取的金融市场股票的历史收盘价数据进行检验和预测，得出对未来三天的预测值与真实值的最大误差不超过0.04。Murat等[3]在对市场压力下的股票市场波动的MIDAS回归预测实验中发现，在采用高频率的数据来估计模型时，GARCH模型具有较好的预测性能，并提出了递推方案可以提高GARCH模型性能的可能性。MIAH等[4]在实验中测试不同滞后阶的GARCH模型，利用Akaike信息准则和贝叶斯准则证明了GARCH(1,1)模型比其他GARCH(p,q)模型对DSE日收益序列的波动性建模效果要好。印凡成等[5]利用GARCH-M模型拟合上证A股指数波动率的变化趋势并进行预测，而后将其应用于Black-Scholes模型中，克服了以往假定有效期内波动率为常数的不合理假设，使预测值进一步趋近实际值。方燕等[6]利用ARIMA-GARCH模型对传媒股价进行研究发现，该模型对具有“尖峰肥尾”分布特征的个股预测相比于传统ARIMA模型和GARCH模型要更加精确。而杨琦等[7]的研究进一步说明了ARIMA-GARCH模型的预测误差会随着预测步数的增加而增大，精度也会越来越低。许舒雅等[8]通过建立ARIMA-GARCH模型对宇通客车的收盘价序列进行拟合并通过实证进行误差分析，得到最小误差为-0.001 272 647 2，证明了该模型可以应用于股票收盘价格的预测。本文在此基础上将波动率代入ARIMA-GARCH中，尝试克服传统股票预测中方差不变的假设，希望将预测精度进一步提高。在实验中发现，该模型对“尖峰肥尾”分布不明显的个股多步数的预测相对较差，但是在下一天的预测与真实值更加接近，因此，利用递归的思想，将第1天的预测值放原始数据中，再重复进行第2天的预测。

1 ARIMA-GARCH-M模型

1.1 ARIMA模型原理

ARIMA模型即差分自回归移动平均模型(Autoregressive Integrated Moving Average Model)，是由Box和Jenkins于20世纪70年代初提出的著名时间序列预测方法，又被称为Box-Jenkins模型。ARIMA模型本质上是通过自相关和部分自相关函数来模拟数据的随机性变化，从而达到预测数据未来变化趋势的目的。ARIMA(p,d,q)模型用公式可以表示为

其中p、d、q分别为自回归阶数、差分阶数和滑动平均阶数，Xt是时间t的时间序列，φi、θj分别是p阶和q阶的平稳多项式算子，εt为一个随机误差项。

1.2 ARCH模型原理

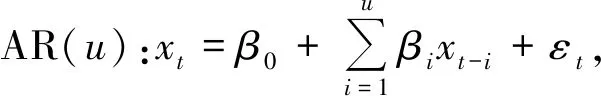
1.3 GARCH模型原理

1.4 GARCH-M模型原理

GARCH-M模型是对GARCH模型的扩展，将波动率作为解释变量代入到时间序列的均值方程中，可以较好地描述收盘价与股价波动的相关性[9],其一般形式可以表示为

1.5 ARIMA-GARCH模型原理

ARIMA-GARCH混合模型是ARIMA模型和GARCH模型结合，可以表示为

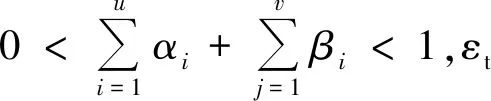
1.6 ARIMA-GARCH-M模型原理

ARIMA-GARCH-M混合模型是ARIMA模型和GARCH-M模型结合，能够更有效地捕捉时间序列的“尖尾”特征，并改善预测结果[10]。该模型表示如下：

其中B为滞后计算。

2 实验研究

2.1 实验步骤

(1)对股票数据进行相关性检验，检验数据之间是否存在自相关；

(2)ADF检验完成对股票价格平稳性检验；

(3)若股票序列为非平稳序列，则对该序列作差分处理，将其转换为平稳序列；

(4)对ARIMA模型作ARCH检验，确定是否存在异方差性；

(5)对ARIMA-GARCH-M模型进行残差检验，检验残差是否符合白噪声，若不符，则需对模型作进一步优化；

(6)在确定ARIMA-GARCH-M模型参数之后，对目标股票进行收盘价单步预测并将预测结果添加到原始数据的下一条数据中；

(7)重复以上步骤，并建立ARIMA模型、GARCH模型、GARCH-M模型、ARIMA-GARCH模型与ARIMA-GARCH-M模型做实验对比。

2.2 相关性检验

随机选取了2018年1月2日—2021年4月2日“平安银行”的790条股票收盘价数据来建立要分析的时间序列模型，部分数据见表1。

首先对股票数据进行DW(Durbin-Watson)检验，DW检验统计量为0.009 336，P为0.000 0。从检验结果看，P<0.005，说明数据之间存在自相关性，因此，可以作时间序列分析。

2.3 平稳性检验

在进行ADF检验前，假设该时间序列为非平稳序列，通过表2的ADF检验结果可以看出，在未进行差分的情况下，P>0.05，不能拒绝原假设，则该序列为非平稳序列。在将该序列一阶差分后，再次进行ADF检验，从表中可看出，差分后P<0.01，则拒绝原假设，该时间序列为平稳时间序列，符合实验要求。

表2 ADF检验结果

2.4 模型选择和参数估计

从一阶差分后的自相关和偏自相关信息中可以大致确定p和q的取值都为(3，4)中的值，为了具体确认p和q的值，结合AIC信息准则，建立多个ARIMA(p，d，q)模型，由ADF检验得d=1，p和q的取值分别从1到4，筛选AIC值最小的一个，最终选出最佳模型ARIMA(4，1，3)，输出结果见表3。

表3 不同阶数模型的AIC值

对于得到的ARIMA(4，1，3)模型，对其进行ARCH检验。检验结果0.262 2,小于F-statistic的1.258 724，因此，该模型存在异方差性，可以建立GARCH-M模型。根据MIAH等[4]的研究结果，这里选取GARCH(1，1)-M。

2.5 ARIMA-GARCH-M模型的建立

由于在该实验中引入了递归的方式，因此每次生成的ARIMA-GARCH-M模型参数是不同的，这里列出第一次预测的模型参数，对后面多次的参数不再列出。

利用ARIMA(4，1，3)-GARCH-M(1，1)-M模型对股票数据拟合，估计模型参数，结果见表4。

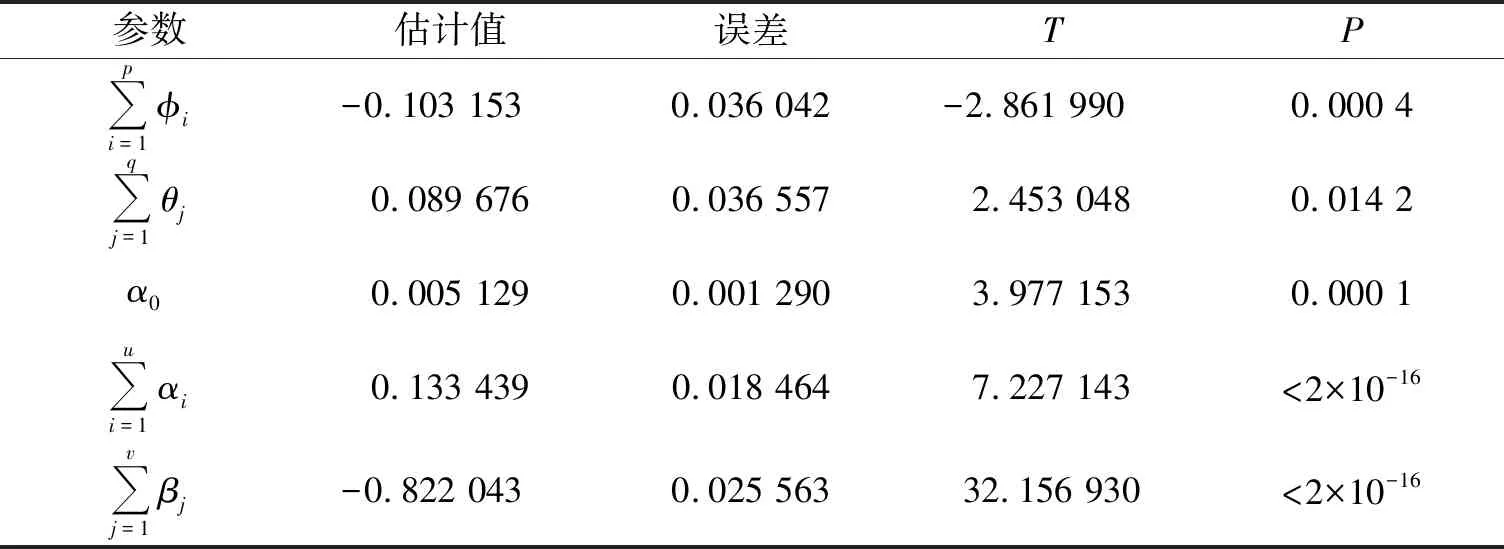
表4 ARIMA(4，1，3)-GARCH(1，1)-M模型参数估计结果

由表4拟合参数可以得到第一次预测的ARIMA-GARCH-M模型：

2.6 模型预测

通过建立的ARIMA-GARCH-M时间序列模型，预测“平安银行”股票4天收盘价，结果见表5。

由表5的预测结果可知ARIMA-GARCH-M模型对“平安银行”股票预测的最大相对误差和最小相对误差分别为-0.260 368 937、0.029 351 052。

2.7 精度比较

为了对比ARIMA-GARCH模型和加入波动率之后的ARIMA-GARCH-M模型的预测效果，使用拟合图像和残差图像来作对比分析,如图1、图2所示。

表5 ARIMA(4，1，3)-GARCH(1，1)-M模型预测股票4天收盘价结果

图1 ARIMA-GARCH拟合残差图 图2 ARIMA-GARCH-M拟合残差图

由于使用的数据量相对较大，从拟合图像和残差图像上难以观察到两者之间的差别，因此，采用方差图像来进一步对比两者的区别，如图3、图4所示。

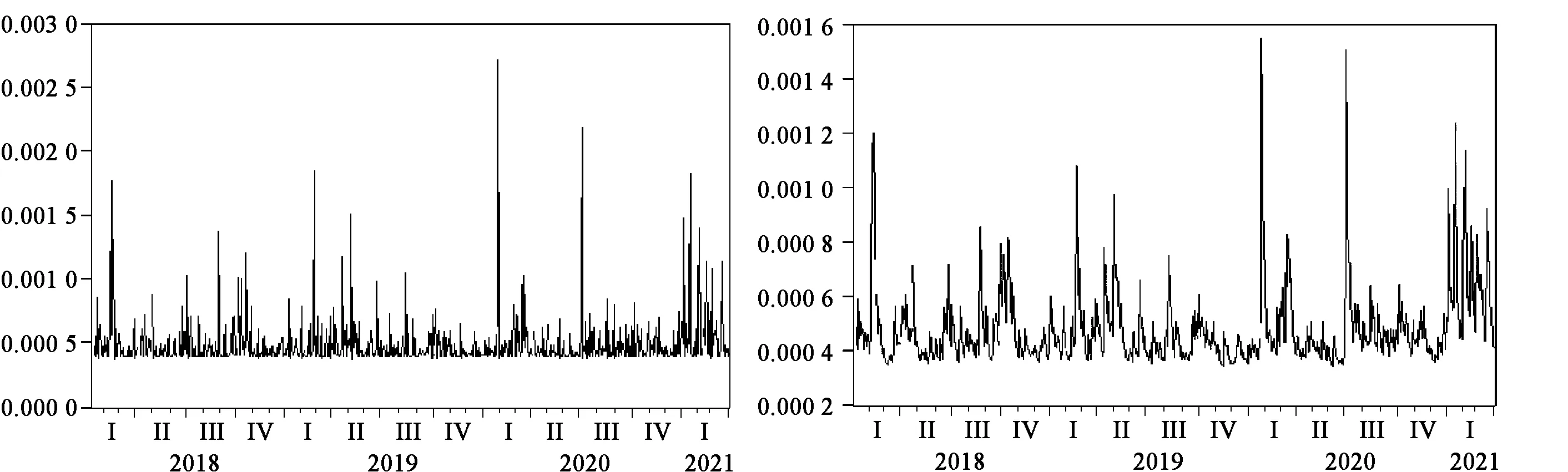
图3 ARIMA-GARCH方差图 图4 ARIMA-GARCH-M方差图

通过方差图像可以明显看出ARIMA-GARCH-M模型比ARIMA-GARCH模型的偏差程度更小。因此ARIMA-GARCH-M模型的预测效果会更优于ARIMA-GARCH模型。

2.8 误差检验与实验对比

为了检验预测的准确性，采用平均绝对误差MAPE、均方根误差RMSE和等系数EC对模型结果进行检验，在实验中发现ARIMA模型在预测出第5天时会出现较大的波动，因此在做实验结果对比时，将预测4期股票收盘价误差检验结果分别对比：

其中N为预测数据天数，ai和ei分别为第i天的实际收盘价和预测收盘价。结果见表6。

根据检验结果，在对股票4天的预测中，ARIMA-GARCH-M模型的平均绝对误差为0.63%，均方根误差为16.09%，等系数为99.63%。传统的ARIMA模型的平均绝对误差为0.72%，均方根误差为17.09%，等系数为99.60%。GARCH模型的平均绝对误差为0.64%，均方根误差为16.20%，等系数为99.62%。GARCH-M模型的平均绝对误差为0.64%，均方根误差为16.08%，等系数为99.63%。ARIMA-GARCH模型的平均绝对误差为0.68%，均方根误差为17.07%，等系数为99.60%。由此可见，在对平安银行股票收盘价的预测中，ARIMA-GARCH-M模型预测结果是优于表6中的其他模型的。

表6 对“平安银行”4天收盘价的预测误差检验结果

3 结论

通过以上实验，可以得到ARIMA-GARCH-M模型在拟合和预测短期股票市场价格上比ARIMA模型、GARCH模型、GARCH-M模型和ARIMA-GARCH模型要更精确一些。对于个人投资者来说，该方法简单有效，可以在日常生活中应用。而对于有更高需求的投资者，想要更加精确地预测出股票的价格，则可以结合庞大的数据量、运用更复杂的模型进行分析，尽可能将更多影响股市价格的因素代入研究中，比如新闻导向、国内政策、投资者购买欲望等。