具有细胞感染的时滞HIV感染模型的最优控制

柳 玉，张正琦

(1.陕西铁路工程职业技术学院 基础课部， 陕西 渭南 714000；2.陕西铁路工程职业技术学院 工程管理与物流学院， 陕西 渭南 714000)

艾滋病毒(HIV)主要攻击人体的免疫系统，从而削弱机体对许多感染和癌症的防御能力，一直是全球主要的公共卫生问题[1]。20世纪后期，Person等[2]借助数学模型研究HIV对感染者体内细胞浓度的影响，这里细胞有未感染的CD4+T细胞、感染的CD4+T细胞和游离病毒。随后，科学家们在此模型上不断改进使其更符合病毒的感染机理，如引入感染中涉及的其他细胞、感染中存在时间滞后的现象、病毒的两种传播方式等。除文献[2]中的细胞外，文献[3-5]等将潜伏的感染CD4+T细胞引入模型。依据是否具有感染性，将感染的CD4+T细胞分为潜伏和感染两类，当感染的细胞浓度很低时，潜伏的细胞可被激活[6]。文献[4-5,7-16]考虑了感染过程存在时间滞后的现象，如病毒进入宿主细胞到其DNA整合至宿主细胞DNA、细胞被感染到产生病毒、药物使用到发挥效用等。大部分HIV感染模型[3-4,8-10]讨论病毒对未感染的CD4+T细胞的感染，即病毒—细胞感染。近些年，临床发现病毒还可通过感染的CD4+T细胞与未感染的CD4+T细胞接触并释放HIV进行感染，即细胞—细胞传播，故文献[5,7,11-16]考虑了病毒的两种传播方式。

基于HIV的两种传播方式，王霞等[5]建立了一类具有潜伏感染细胞的时滞HIV感染模型：

(1)

讨论了模型(1)各平衡点的全局稳定性，并利用数值模拟进一步验证了结论。HIV感染者的最优治疗策略一直受到广泛的关注，如文献[7-10]考虑使用逆转录酶抑制剂(RTIs)和蛋白酶抑制剂(PIs)两种抗病毒药物的最优治疗策略。药物RTIs主要作用于抑制病毒感染未感染的CD4+T细胞，而PIs主要作用于抑制病毒产生和抑制感染的CD4+T细胞感染未感染的细胞[7]。

在模型(1)的基础上，本文增加考虑两种抗病毒药物RTIs和PIs的治疗，同时，注意到药物使用到发挥效应存在时间滞后的现象。假设t时刻RTIs作用于抑制病毒感染未感染的CD4+T细胞的治疗效果和时滞分别为u1(t)和ε1，t时刻PIs作用于抑制病毒产生的治疗效果和时滞分别为u2(t)和ε2，t时刻PIs作用于抑制感染的CD4+T细胞感染未感染的细胞的治疗效果和时滞分别为κu2(t)和ε3，其中κ为常数且0<κ≤1，建立如下模型：

(2)

其中T(t)、L(t)、I(t)、V(t)分别表示t时刻未感染的CD4+T细胞、潜伏的感染CD4+T细胞、感染的CD4+T细胞、游离病毒的浓度。s为未感染的CD4+T细胞的产生率，k1为病毒—细胞感染方式下的感染率，k2为细胞—细胞感染方式下的感染率，f、η∈(0,1)为常数，分别表示病毒—细胞感染和细胞—细胞传播下产生潜伏的感染CD4+T细胞的概率，α为潜伏的感染CD4+T细胞被激活的速率，N为感染的CD4+T细胞在其生命周期释放病毒的平均数，μT、μL、μI、μV分别为未感染的CD4+T细胞、潜伏的感染CD4+T细胞、感染的CD4+T细胞、游离病毒的死亡率，τ1表示从HIV进入宿主细胞到其DNA整合至宿主细胞DNA上的时间，τ2表示从细胞被感染到产生病毒的时间，e-δ1τ1、e-δ1τ2分别为τ1、τ2下感染的细胞存活的概率。定义容许控制集：

U={ui(t)|ui(t)可测，0≤ui(t)≤1，t∈[0,tf]}，

其中i=1,2；tf表示有限治疗时间内的末端时刻。假设系统(2)满足初始条件：

(3)

1 最优控制问题

在HIV治疗过程中，人们通常希望在有效的治疗时间内使游离病毒的浓度和药物副作用尽可能小。于是本文以两种药物RTIs和PIs的治疗效果u1(t)和u2(t)为控制变量，以游离病毒的浓度和药物副作用尽可能小为目标，提出系统(2)的最优控制问题。定义目标函数为控制变量u1(t)和u2(t)的一次函数，即线性控制的目标函数：

(4)

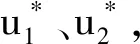
定义目标函数为控制变量u1(t)和u2(t)的二次函数，即二次控制的目标函数：

(5)

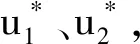
为便于后续最优控制特征的讨论，记

Tτ1(t)=T(t-τ1)，Tτ2(t)=T(t-τ2)，

Iτ1(t)=I(t-τ1)，Iτ2(t)=I(t-τ2)，

Vτ1(t)=V(t-τ1)，Vτ2(t)=V(t-τ2)，

u11(t)=u1(t-ε1)，u22(t)=u2(t-ε2)，u23(t)=u2(t-ε3)。

2 线性控制下最优控制的特征

定义Hamiton函数

H1(T,Tτ1,Tτ2,L,I,Iτ1,Iτ2,V,Vτ1,Vτ2,u1,u11,u2,u22,u23,λT,λL,λI,λV)=

V+α1u1+α2u2+λT[s-μTT-(1-u11)k1TV-(1-κu23)k2TI]+

λL[(1-u11)fk1Tτ1Vτ1e-δ1τ1+(1-κu23)ηk2Tτ1Iτ1e-δ1τ1-(α+μL)L]+

λI[(1-u11)(1-f)k1Tτ2Vτ2e-δ1τ2+(1-κu23)(1-η)k2Tτ2Iτ2e-δ1τ2-μII+αL]+

λV[(1-u22)NμII-μVV]，

(6)

其中λT、λL、λI、λV均为协状态变量。

由多时滞最优控制的最小原则[17]得，协状态方程为

(7)

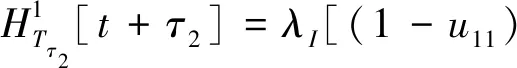
对于系统(2)，由于治疗的初始时刻为0，末端时刻tf和初始条件(3)均已知，故横截条件为

λT(tf)=λL(tf)=λI(tf)=λV(tf)=0。

(8)

由Hamiton函数(6)得，转化函数为

(9)

其中

(10)

其中i=1,2。

3 二次控制下最优控制的特征

定义Hamiton函数

H2(T,Tτ1,Tτ2,L,I,Iτ1,Iτ2,V,Vτ1,Vτ2,u1,u11,u2,u22,u23,λT,λL,λI,λV)=

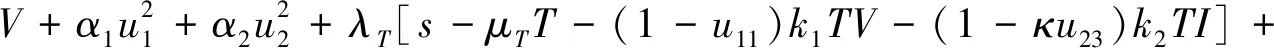
λL[(1-u11)fk1Tτ1Vτ1e-δ1τ1+(1-κu23)ηk2Tτ1Iτ1e-δ1τ1-(α+μL)L]+

λI[(1-u11)(1-f)k1Tτ2Vτ2e-δ1τ2+(1-κu23)(1-η)k2Tτ2Iτ2e-δ1τ2-μII+αL]+

λV[(1-u22)NμII-μVV]，

(11)

由多时滞最优控制的最小原则[17]得，协状态方程和横截条件同线性控制的目标函数(4)下的协状态方程(7)和横截条件(8)。

依据Hamiton函数(11)得

(12)

其中

(13)

其中i=1,2。

4 数值模拟

利用LINGO和MATLAB结合，进一步分析在线性控制目标函数(4)和二次控制目标函数(5)下，药物RTIs和PIs的最优治疗策略及有无治疗对系统(2)中细胞浓度的影响。

由文献[3,5,7,16]，假设药物治疗末端时间为50 d(即tf=50 d)，系统(2)中参数分别为s=1 mm-3·d-1，k1=2.0×10-3mm3·d-1，k2=3.0×10-3mm3·d-1，α=0.01 d-1，μT=0.1 d-1，μL=0.004 d-1，μI=0.26 d-1，μV=2.4 d-1，N=2000，κ=0.4，f=η=0.005，初始条件为

其中τ1=0.25 d，τ2=0.5 d，ε1=0.2 d，ε2=0.1 d，ε3=0.5 d。目标函数(4)、(5)中权重系数取α1=5，α2=100。

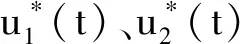
由图1(a)和图1(b)可知，在治疗期内，药物RTIs和PIs的最优治疗策略为间断的，其中RTIs在前2 d和6～46 d左右的最优治疗效果为1，而PIs在前6 d左右的最优治疗效果为1，其余时间药物的最优治疗效果为0。由图1(c)—(f)可知，相比于无治疗，在最优治疗策略下未感染的CD4+T细胞浓度明显增加，其他细胞浓度均减少。

(a)最优治疗策略随着时间t的变化图 (b)最优治疗策略随着时间t的变化图

(c)有无治疗对T(t)的影响 (d)有无治疗对L(t)的影响

(e)有无治疗对I(t)的影响 (f)有无治疗对V(t)的影响图1 在线性控制目标函数(4)下，最优治疗策略及有无治疗对细胞浓度的影响

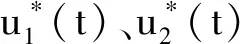
由图2(a)和图2(b)知，在治疗期内，药物RTIs和PIs的最优治疗策略为连续的。对比图1和图2可知，在两类目标函数下，药物RTIs和PIs的最优治疗策略不同，但对细胞浓度的影响相似。

(a)最优治疗策略随着时间t的变化图 (b)最优治疗策略随着时间t的变化图

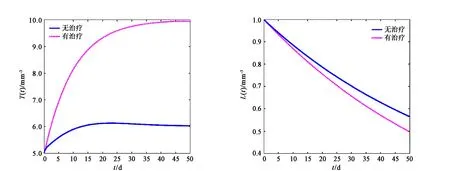
(c)有无治疗对T(t)的影响 (d)有无治疗对L(t)的影响

(e)有无治疗对I(t)的影响 (f)有无治疗对V(t)的影响图2 在二次控制目标函数(5)下，最优治疗策略及有无治疗对细胞浓度的影响

5 结 论

本文通过控制RTIs和PIs两种抗病毒药物的治疗效果，以在有限的治疗时间内实现游离病毒浓度和药物副作用尽可能小的目标，探究了一类具有细胞感染的HIV感染模型的最优控制问题，其中HIV感染模型考虑了药物使用到发挥效应存在时间滞后的现象。首先，定义了线性控制和二次控制两类目标函数，提出了相应的最优控制问题；其次，利用多时滞最优控制的最小原则，分析了在两类目标函数下最优控制的特征；最后，通过LINGO结合MATLAB进行数值模拟，得到两类目标函数分别对应的药物最优控制策略及有无治疗对细胞浓度变化的影响。结果表明，相比于无治疗，在最优治疗策略下未感染的CD4+T细胞浓度明显增加，其他细胞浓度均减少，同时，在两类不同的目标函数下，药物RTIs和PIs的最优治疗策略不同，但对细胞浓度的影响相似。线性控制目标函数(4)对应的最优控制策略为间断的，而二次控制目标函数(5)对应的最优控制策略为连续的，故线性控制目标函数(4)对应的最优控制策略更易在临床中实现。