基于二进小波的人脸特征提取与检索

阿斯古丽·艾合麦提，吐尔洪江·阿布都克力木，赵思温

（1.昌吉学院数学与数据科学学院，新疆昌吉 831100；2.新疆师范大学数学科学学院，新疆 乌鲁木齐 830017）

二进小波变换在人脸图像特征提取尤其是在边缘检测方面应用广泛，基于单个特征的人脸图像特征提取方法不能够无缺且足够地描述图像的内容信息[1]，因此，文中用二进小波变换进行边缘检测，提取人脸图像的相关信息，将颜色、形状、纹理3 种人脸特征矢量数据进行融合和分析，并作了相关研究。虽然目前部分研究人员已经给出了将颜色、纹理以及形状特征中的两个特征融合的图像特征提取及检索算法，但是由于提取的单个特征算法的效果不理想[2]，因此文中需要对单个特征提取算法进行改进，最终融合多种特征，从而描述图像的内容信息，以此达到较优的效果。

1 二进小波变换

定义1[3]令函数若存在常数A、B且满足0 ＜A≤B＜∞，使得：

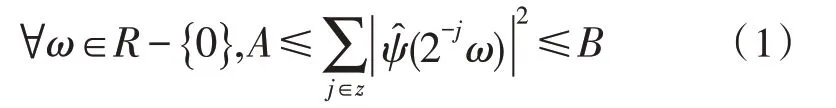
则称ψ(t)为二进小波，式（1）叫做二进小波的稳定性条件。当A=B时，称为最稳定条件。

定理1[4]（二维àtrous 算法）

需要说明的是，提出的àtrous 算法是在Mallat 创建的算法基础上修改得到的。其分解公式如下：

2 人脸特征提取方法

2.1 环色直方图特征提取

假设尺寸为M×N的图像用I表示，图像已量化的彩色边缘用F表示，P=(x,y),(x,y)∈F代表彩色边缘F内所有像素点的组合。|P|代表边缘点的集合表示彩色边缘的中心点，包括计算求出以C点为圆心的最大半径为将半径R用正整数n平分，求出每个等分的数值，之后以中心点C为圆心，以(k×R)/n(1≤k≤n)作为半径，能够计算出数量为n的圆环边缘个数，那么由内到外每个环和P的交集把P分成P1,P2,…,Pn。假定Pk代表第k个圆环的边缘点个数，Hk为根据第k个圆环灰度出现的频率数值，通过汇总分析绘制一维直方分布图，计算方法是：分析各圆环Pk的颜色数值是j(j=0,1,…,255) 的像素数量hk,j=sum{P(x,y):P(x,y)=j,∀(x,y)∈Pk}，进而可以绘制出彩色边缘环形颜色直方分布图[5]：

2.2 二进小波变换的边缘梯度特征提取算法

1）基本原理

如果F图像具有N×N个像素，那么F=fn,m,n=0,1,2,…,N-1，m=0,1,2,…,N-1 因此首先按照连续图像提取的方法，利用小波变换对图像边缘进行提取。由于在实际的操作中会受到环境和其他因素的影响，所以数字图像基于二进小波变换的边缘提取计算方法如下：

①参数取离散值a=2-j，计算求出F图像的二维小波变换值W1f(2-j,n,m)、W2f(2-j,n,m)，n,m=0,1,2,…,N-1，其中既可以按照传统的三层分解，也可以根据用户的选择分解层数。通过如下两种方法得到二维小波变换：一是连续小波变换，即将计算出的离散数值在图像中表现出来，变成连续信号，再求出连续小波变换在不同尺度下的小波系数；二是二进小波变换，即使用合适的小波和滤波器组，然后对数字图像信号与滤波器通过卷积可求出二进小波变换，计算出不同尺度下的小波系数。

②对所有像素(n,m)求出梯度值以及它们之间夹角Af(2-j,n,m)的正切函数值[6]。

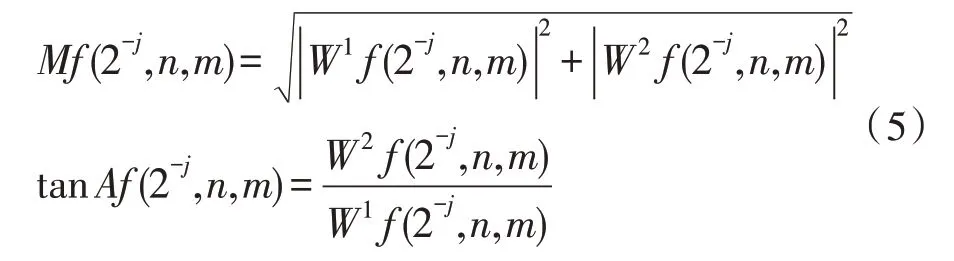
③求边界点：确认阈值T＞0，因此n,m=0,1,…,N-1。如果W2f(2-j,n,m)≥T，那么由W2f(2-j,n,m)计算出局部模极大数值，则(n,m)是模极大点，同时也成为了一个边界点。但是判断离散图像中一个像素点(n,m)是不是模极大数值点和连续图像对比不会有差异，根据图像的构成可以看出，在单个像素点取相邻点时可以选择不同的个数，如4、8、16 等，可以根据实际需求选择。文中按照8 个邻接点的方法，将平面分成8 个不同的区域。这8 个分区依次由22.5°、67.5°、112.5°、157.5°、-157.5°、-112.5°、-67.5°、-22.5°组成。受到梯度方向对称性的影响，使用4 个扇区1、2、3、4 中的梯度方向，各自的像素点(n,m) 及tanAf(2-j,n,m) 需 在4 个区域之中。可以用CodeAf(2-j,n,m) 标 记tanAf(2-j,n,m)所进入区间的编号，将Mf(2-j,n,m)和分区CodeAf(2-j,n,m)在各自梯度方向邻近像素的模值进行对比[7]。

④连接各尺度上的边缘点，构成各自边缘的极大曲线图。在离散条件下，极大曲线是根据图像离散采样各邻近的边缘点(n,m) 和(n,m)+γ(n,m) 相连生成的曲线，包括γ(n,m)正交于CodeAf(2-j,n,m)的梯度角度[8]。根据原始图像和二值边缘的互相影响，计算求出原始图像的彩色边缘数据。所以必须选用性能优良、符合实际的小波函数和滤波器，以便更好地进行边缘检测。第一种和第二种二进制小滤波器系数分别如表1 和表2 所示。用两种二进制小滤波器系数的边缘检测，结果图如图1-2 所示。

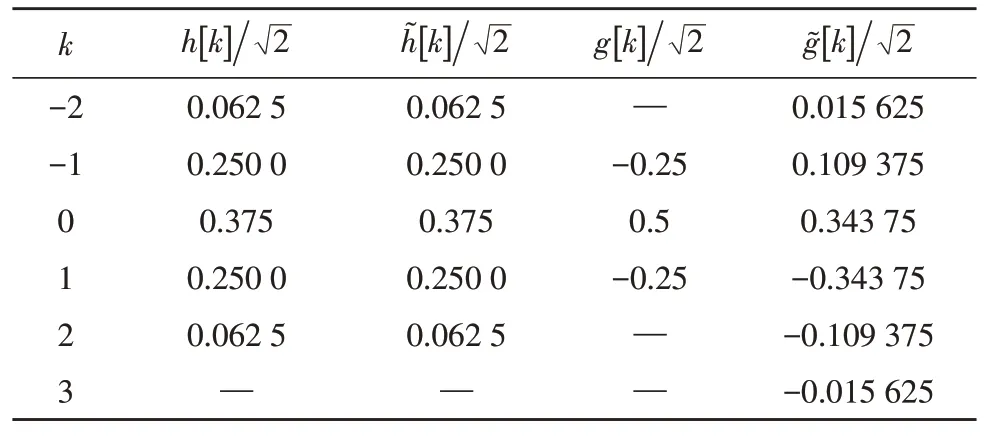
表1 第一种二进小波滤波器系数

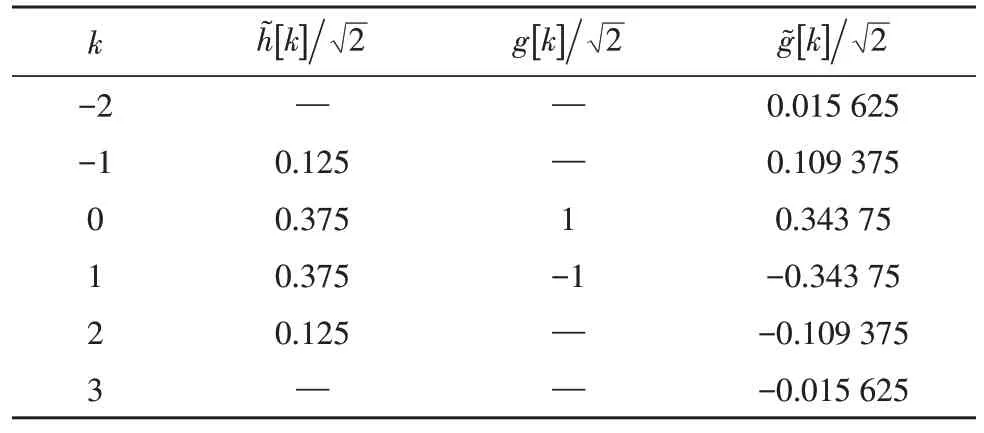
表2 第二种二进小波滤波器系数

图1 用第一种二进小波滤波器系数的边缘检测结果图

从图1 和图2 可以看出，图2 的边缘细节比图1的多，边缘细节越多，对后面的实验越有利。

图2 用第二种二进小波滤波器系数的边缘检测结果图

2）算法步骤

计算小波模极大数值环形直方图结构数值的方法如下：将径向尺寸R平均分成m等份，然后以(k×R)/m(1 ≤k≤m)为半径绘制圆环，由此得到数量为m的多个同心圆环，在每个圆环和P的交叉处可以求出边缘图像点的数值根据第m个圆环内的所有边缘点，求出在边缘线上的点的小波模极大数值累计结果，根据结果绘制小波模极大值环形直方分布图[9]。

文中绘制边缘梯度直方分布图的主要步骤如下：①根据二进小波模极大值计算出边缘点的数值。②求出边缘图像的梯度角度Aa f(x,y)，并将弧度转换为度。③依据边缘像素点的梯度数值绘制边缘梯度方向直方分布图H(i)。具体实现的过程为：将梯度角度Aa f(x,y)∈[0°～360°]平均分成L个区域，汇总区间内包含的边缘个数，那么n(i)的区间数值是：

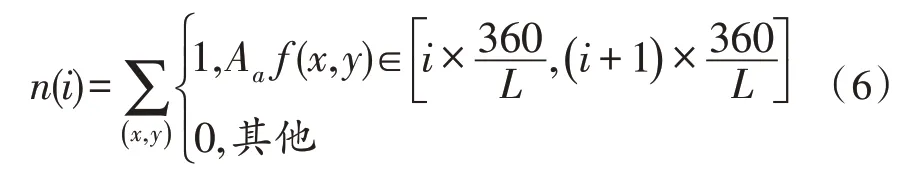
为了使边缘梯度方向直方图对图像光照变化、平移变化、尺度变化具有不变性，根据边缘像素计算结果，绘制出边缘梯度方向的直方分布图H(i)[10]。在直方分布图H(i)中，L的数值影响和角度量化之间成正比，L的数值越大，角度量化的变化越多。根据以上计算结果，在直方分布图H(i)中，横坐标中每一个角度单位量化数值为8，角度是45°，纵坐标表示的是角度单位的像素占所有边缘像素的比值，得到的一维边缘梯度方向直方图函数如下：

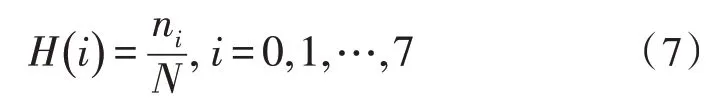
式中，ni代表边缘处的梯度方向角在i×45°～(i+1) ×45°范围内的像素数量，N代表边缘像素点的总数值[11]。

2.3 LBP特征提取

根据图像的尺寸M×N调整图像的比例，在图像左上角设置滑动区域，然后按照一定规律来移动邻域，并对邻域内的图像块进行预先设置的运算[12]。待该邻域运算结束后，便将领域向右或向下移动一步，再作相同处理，直至覆盖图像中所有的像素点。特征提取之前，需要设定领域尺寸以及移动步长（文中设定两个像素点之间的距离为一个步长）。一般按照从上到下、从左到右的顺序，从图像的左上角入手，参照一定的比例尺寸开始移动，根据获得的图像像素进行卷积计算，通过计算结果可看出图像的纹理特性。

3 三个特征融合的原理和实验结果分析

利用之前所描述的3 种方法，即环形颜色直方图、二进小波边缘梯度特征的直方图以及LBP 算子对图像的实际内容进行表达，完成了以3 种特征结合为基础的图像特征提取与检索。若将Q看作待特征检索的图片，把I看作图像库的图片，那么这两个图片的彩色边缘环形颜色直方分布图类似程度则可以表示为其中分别可看作I、Q第k个圆环的颜色直方分布图序列；可看作是需要检索的图片于第k个圆环的彩色边缘个数[13]。可以把 |P|看作需要检索图片所有边缘的数量，把ωk看作权值，该数值考虑到了各个点在所有圆环里分布的情况，其目标为增加关键区域类似对总体相似程度的干扰。

可把S=[S1,S2,…,SM]看作是已经归一化处理的小波模极大数值环形直方分布图，那么已经归一化的边缘梯度直方图可写作那么D2=D(SQ,SI),D3=D()则表示彩色边缘环形颜色直方分布图和已经归一化处理的小波模极大数值环形直方分布图的相似程度[14]。因此，随机两张图片的相似程度可表示为D(I,Q)=w1D1+w2D2+w3D3，其中，w1、w2、w3代表3 类特征相似性程度所设置的权值，且符合w1+w2+w3=1[15]，三类权值可选择为w1=0.3、w2=0.4、w3=0.3。

4 结论

利用3 种方法，即环形颜色直方图、二进小波边缘梯度方向直方图以及LBP 算子来描述人脸图片信息，在两种不同的人脸数据库里通过软件Matlab 进行模拟分析；同时，对照了两种不同的二进小波滤波器的边缘检测结果图。为了更深入地检验提出方法的有效性，将其与现阶段的相同种类方法进行了比较。文中所使用的3 种方法蕴含了图像多层人脸图像内容，互相补充地描述了图片重要信息，还确保了其旋转不变性、平移不变性以及尺度不变性，且抗干扰能力较好[16]。