基于对偶方程有限元法的电阻参数提取

张 程，徐小宇，任卓翔

（1.中国科学院微电子研究所，北京 100029；2.中国科学院大学，北京 100049；3.索邦大学，巴黎 75006）

集成电路加工工艺不断更迭，器件特征尺寸不断减小，集成度的不断提高使得电路信号延迟，功耗等问题不断加剧。就集成电路设计中的电路参数提取环节而言，寄生电容与电阻会产生RC 延迟，影响电路信号的同步。电路参数提取的结果必须达到一定的精度才能保证电路能够实现其设计功能。以手机、显示器的显示屏信号线等特定电路为例，为保障各个像素点的同步刷新，各个线路上的信号延迟必须保持同步，这就需要精确地对电路进行电阻和电容参数提取分析[1-9]。

电阻和电容等参数提取通常采用有限元法等数值算法[10-12]，根据目标问题对应的物理系统建立偏微分方程以及设定适当的初始条件，通过场分析获取电路系统的电阻参数。由于求解精确度要求的提高，需要将求解域剖分非常细密的网格才能得到较为理想的解，使得计算效率低下[13-14]。在近年来电磁学对偶方法的发展与应用的基础上，该文引入电流场对偶方程方法[10,15]，以提升场求解与参数提取的效率，并通过实际算例求解验证所提出方法的精确性与高效性。

1 稳恒电流场的对偶有限元法

1.1 稳恒电流场的控制方程

其中，σ为导电媒质的电导率。根据电荷守恒定律，从电流场中任一闭合曲面S流出的电流应等于单位时间内该面所包围空间V的电荷的减少量，即：

将所研究闭合面不断缩小至一点，得到：

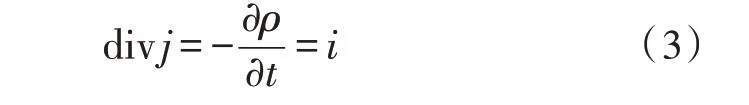
其中，ρ为电荷密度，i为电流源。设空间某点的标量电势为v，则有e=-gradv。进而可以得到：

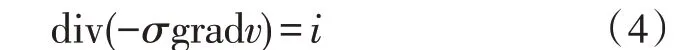
将以上所得方程与静电场方程进行类比[11,15]，d为电位移矢量，ε为介电常数，静电场问题可以描述为：

可以看出，静电场与稳恒电流场在数学形式上十分相似。根据麦克斯韦方程组，稳恒电流场与静电场均为无旋场，满足：

对于静电系统，电容提取需要模拟导体间的静电场，其电场分布与系统中各带电体的相对位置、形状、尺寸和电介质的分布有关，其能量分散在导体周围的空间中。电阻提取需要模拟导体内的稳恒电流场。对比于静电场，由于电流、能量总是被约束在导电线路中，稳恒电流场的计算分析相对容易。

1.2 对偶格式的有限元法控制方程

实际问题中的研究区域多为不规则几何体，为了更好地适应不同的复杂结构，三维有限元法可采用四面体单元网格对所研究的空间Ω进行离散（如图1 所示的四面体单元ijkl），并在各个离散单元上建立单元矩阵方程。

(1)患者一般情况及疼痛部位、性质、评分、不良反应;(2)患者服药情况,包括镇痛药名称、剂量、用法、不良反应等;(3)患者的心理状态及情绪;(4)遵医行为的评估以及饮食管理;(5)工作与休息管理,是否因疼痛影响日常活动及休息,是否与家人、朋友能融洽相处。每周由护理联络员对护理干预内容进行收集,由资料收集员对数据进行纵向对比与总结。

通常，有限元法将单元节点上的标量电势作为未知量，建立单元方程，如图1中节点i上的电势vi。对于体单元棱边上的矢量电势，同样也可以作为未知量建立单元矩阵方程，如图1中体单元棱边ij上的uij，满足：

图1 有限元法四面体单元的节点编号及自由度位置

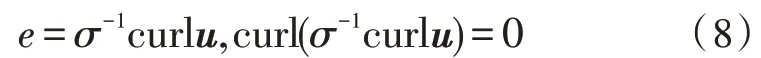
其中，矢量u可以理解为恒流场中的电流矢量位，通过式（4）与式（7），可以分别推导出二者相应的方程：

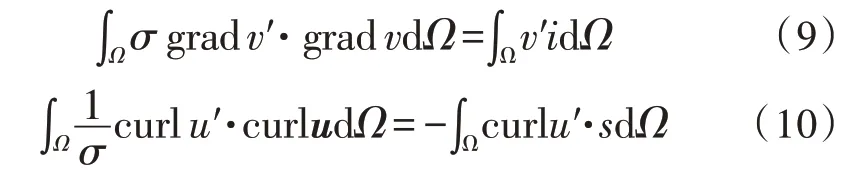
采用矢量电势作为未知量会导致多值问题，因而，需要加入“连接”（link）结构来连通所有Dirichlet边界（即有外加电压的区域），也就是式（10）中的右端项所描述的部分。两种方法对应的单元材料矩阵分别采用基于Whitney 棱单元ωe和面单元ωf的伽辽金方法来获得[11]，即：

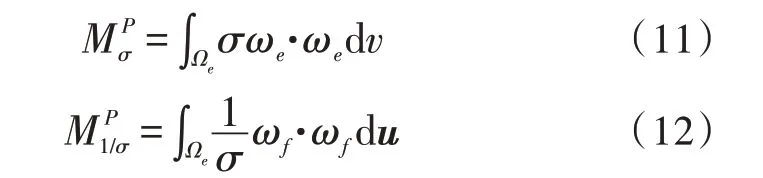
以上两种方法分别称为点单元法（又称标量有限元法）和棱单元法（又称矢量有限元法），它们构成对偶关系，因此也分别称为原始（Primal）方法和对偶（Dual）方法。

2 电阻及电阻网络

对多端口电路，端口两两之间存在互电阻，从而组成待提取的电阻网络。对于具有n个端口的电路，当计算其第i个端口与其他端口之间的电阻时，可在第i个端口上施加1 V 的电压，其他端口上施加0 V 电压，通过上述恒流场分析计算得到各互电阻值Ri，也可推知，第i个端口自电阻的倒数等于与之关联的所有互电阻倒数之和。当需要计算电路中所有互电阻时，则需要对所有端口逐一按照前述步骤进行一次计算。

以图2中的三端口线路模型为例[10,16]，当给#1端口施加1 V电压（作为主端口），而#2，#3施加0 V电压（作为相关端口，或次端口，或从端口），可以计算得到电阻R12、R13，并以此推得自电阻R11，依次将其他端口作为主端口，计算互电阻与自电阻，从而得到电阻矩阵R。

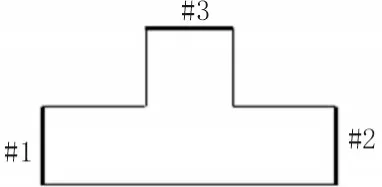
图2 两种多端口线路模型示例

理论上，只需要计算出电阻矩阵的上三角部分（不含对角线）即可推得整个电阻矩阵，即：

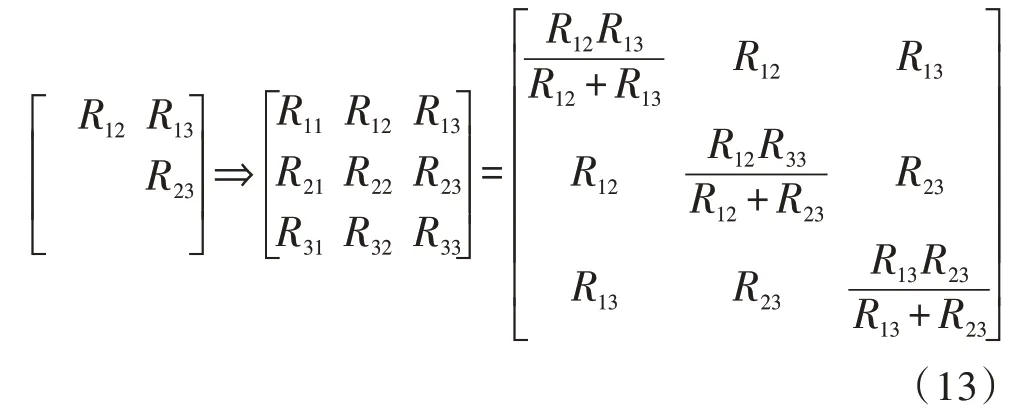
在实际工程应用中，也可以通过该方式节省计算时间。

对于某些只需关心其中部分电阻的问题，根据需求设定相应的主端口即可。

3 算例验证

3.1 算例模型

在实际电子工程设计中，电路连接线的模型结构有多种形式，这些连接线路担负着电能输送或者信号传递（或兼而有之）的任务，而针对电路连接线上的电阻参数提取对于电路整体的场分布、电能损耗、热效应、信号延时等分析都有着重要意义。这里选取一种电路连接结构作为典型算例，如图3所示。该连接结构整体材质为铜（电导率σ取5.998×107S/m），其总体轮廓为L 型，宽为1.70 cm，高为0.74 cm。提供4个端口接入电路。

图3 一种金属导线连接结构

3.2 建立连接

对于电流场的有限元对偶方程方法，在基于棱单元法计算电场分布时，为避免多值问题，需要预先建立各Dirichlet 边界（也就是从端口到端口）及多连通域之间的连接，如图4 所示。

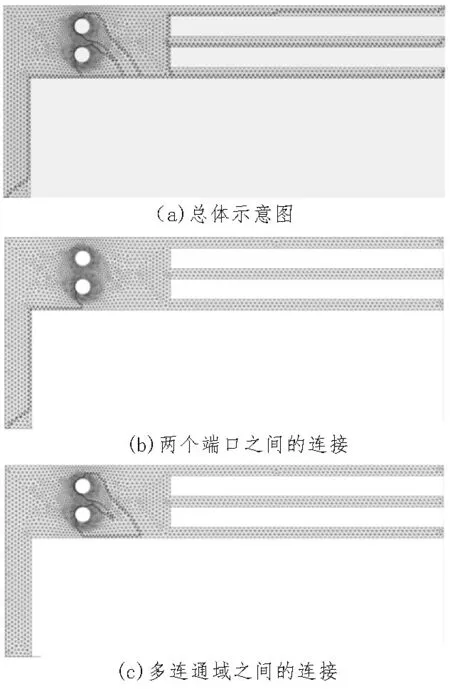
图4 各端口及多连通域之间的连接

3.3 电阻参数提取结果

依照上文所述提取电阻矩阵的流程，分别将电路中各个端口设为主端口,得到相应的场分布结果（如图5 所示是以#1 作为主端口的示例），以及对应的电阻参数矩阵，如表1 所示。

表1 电阻参数提取结果

图5 电场分布情况

3.4 随网格加密的收敛性

一般情况下，以电路中#1 和#4 端口的互电阻提取为例，不断加密所研究区域的网格，得到的电阻参数如表2 所示，并将其与参考值0.821 284 μΩ进行对比，参考误差如表3 所示，可以看出，通过利用对偶方程方法，即使在稀疏的网格条件下也能够获得精确的解；随着对研究区域剖分网格的不断加密，原始解与对偶解的误差不断减小，并趋于一致。

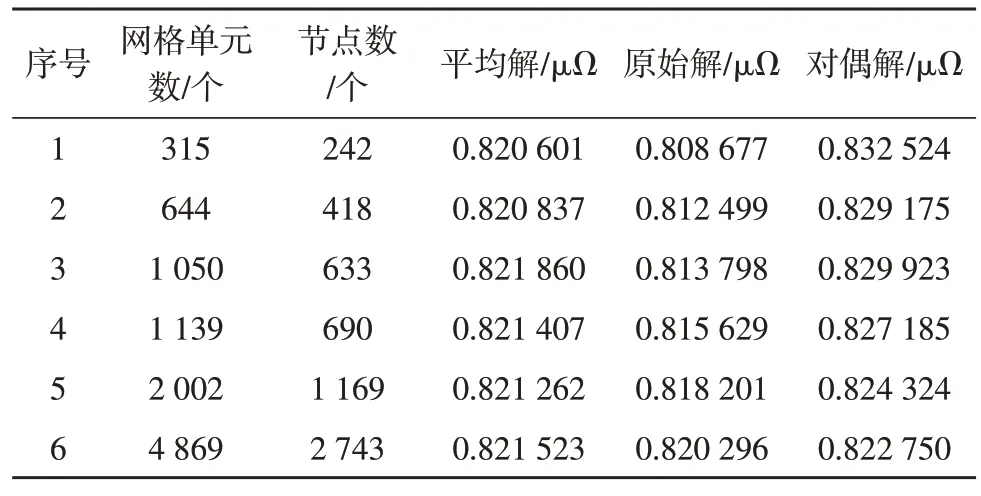
表2 #1与#4端口互电阻参数提取结果

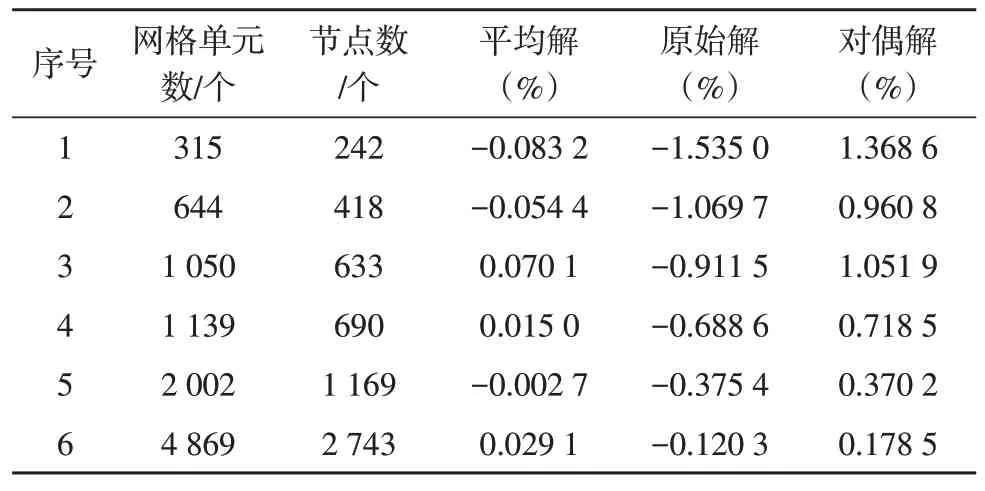
表3 #1与#4端口互电阻参数提取结果的参考误差

将表2 中的平均解、原始解、对偶解随网格加密的计算结果绘制成图，如图6 所示。由此可以发现，端口#1 和端口#4 之间互电阻的原始解与对偶解分别从上、下方收敛逼近至参考解，显示出上、下界以及互补特性，这也表明对偶解与原始解分别低估和高估了电流系统的能量，同时采用原始方程和对偶方程两种方法，取两者解的平均值，可以在网格剖分较为稀疏的情况下获得近似精确的结果。其中，参考解是利用有限元法，采用极为稠密的网格计算得到的，经验上可以视为近似精确解。

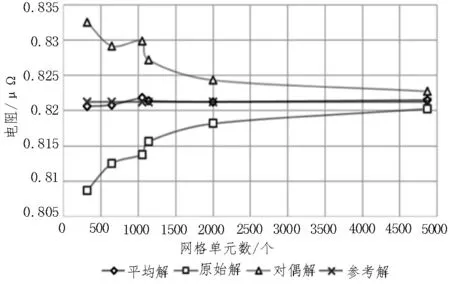
图6 端口#1、#4互电阻随网格加密的变化

3.5 其他算例

该文将所提出的方法用于如下多种常见结构的电阻提取，进一步验证了方法的有效性。

1）带孔洞的导体两端的等效电阻提取

算例如图7 所示，所提取的线电阻值取为0.135 4 μΩ，具体如表4 所示。

表4 带孔洞的导体电阻参数提取结果

图7 带孔洞的导体电阻提取算例

2）蛇形线路

蛇形线路常见于显示屏的布线[10，16],可以视作两端口的导体电路，如图8 所示。所提取的电阻值取为5.245 8 μΩ，具体结果如表5 所示。

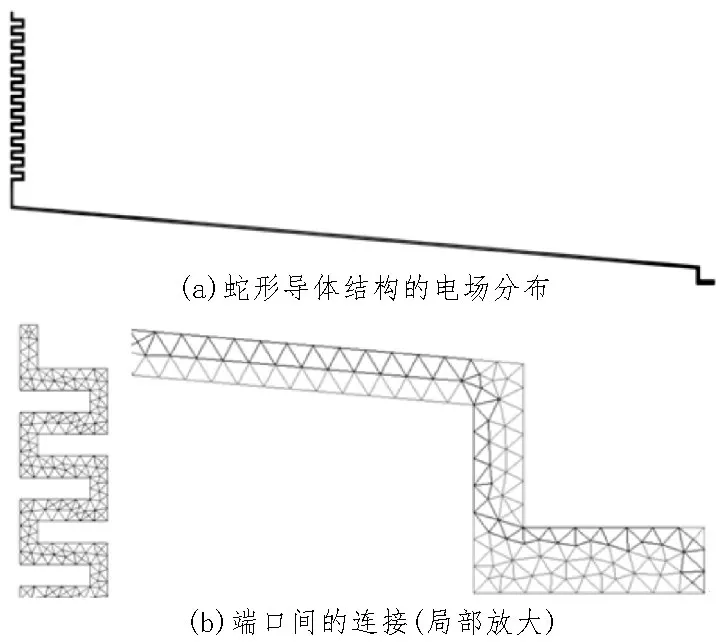
图8 蛇形导体电阻提取

表5 蛇形导体电阻参数提取结果

4 结论

该文在利用有限元法提取电路电阻参数矩阵的基础上引入了电流场的对偶方程方法，即点单元法与棱单元法，同时为了避免在采用矢量电势作为未知量时会出现的多值问题，通过建立从端口到端口或多连通域的连接，以使所列的线性方程组有唯一解。

通过分析算例计算结果可以发现，随着网格剖分的不断加密，即所研究区域的单元数与节点数不断增加，使用点单元法所得的原始解与使用棱单元法所得的对偶解有逐步收敛的趋势，原始解从参考值的下界开始收敛，对偶解从参考值的上界开始收敛，两者具有一定对称性，也就是说，对于所研究的电流场问题，原始解与对偶解在电路系统中的能量具有互补关系，将该特性应用于相关电路的电阻参数提取过程中，能够使计算效率得到大幅提升，即当所研究区域网格剖分较为粗糙时，同时采用这两种对偶方法，取原始解与对偶解的平均值作为最终解，其结果具有相对较小的误差，从而保证了最终的求解精度。若只利用有限元法进行计算，需要剖分非常精细的网格才能达到与参考值相当的计算精度，并伴随急剧增加的计算量，当问题尺度较大时，求解效率大幅降低。综上所述，通过利用对偶方程有限元法，不仅可以极大地提高电路电阻参数矩阵的提取效率，同时还能够保证精确性，解决了针对复杂结构的电路电阻提取效率低、精度差的问题。