基于麦可纳姆轮动力学特征建模在模型预测控制中的应用
2022-08-17荆学东杜黎童
马 俊,荆学东,杜黎童,詹 佳
(1. 海装项目管理中心 潜艇室,北京 100000;2. 上海应用技术大学 机械工程学院,上海 201418;3. 上海船舶设备研究所,上海 200031)
0 引言
随着《中国制造2025》强国战略的要求陆续推行,移动机器人技术在制造业、服务业、医疗业等生产生活中取得了快速的发展与应用,市场上现有的移动机器人大多为四轮差速驱动,该驱动方式的机器人运动灵活性差、精度低,应用范围局限性高,不能很好的发挥出移动机器人应有的性能特点[1]。因此开发出高机动性、高精度的全向移动机器人成为世界各国移动机器人技术攻坚的关键核心点。目前全向移动机器人的技术研究主要包括模型建立、控制、导航定位和路径规划等[2-5]。
全向移动机器人的控制是指通过输出控制电机的角速度的大小和方向来驱动机器人按照预设的路径行驶[6]。目前主要应用的轨迹跟踪方法包括各种改进的PID控制[7-8]、滑模控制[9]、反演控制[10]、鲁棒自适应控制[11]、模型预测控制等。文献[12]余红英等在智能驾驶中引入PID控制,但由于PID调参比较麻烦,构建的PID控制器无法精确控制车辆的轨迹跟踪。马海涛等[13-14]设计了滑模控制器用于轨迹跟踪,该控制器因滑模方法的特性容易引起“抖振”现象,实际控制效果不是十分理想;文献[15]针对机器人模型参数不确定性问题,设计了鲁棒自适应控制器,提高了移动机器人轨迹跟踪的鲁棒性;文献[16]建立了双输入-双输出的非线性运动学模型,提出了一种融合偏差智能转化评价函数法和指数稳定控制的控制方法,但模型复杂性高、计算量大;GUO等[17]将自适应控制方法和滑模控制方法相结合设计横向自适应模糊滑模控制器,提高了智能车辆轨迹跟踪精度和响应特性。模型预测控制(Model Predictive Control,MPC)是一种动态规划方法,由于其具备对系统模型要求低、鲁棒性和抗干扰性好的特点,被广泛应用于智能机器人轨迹跟踪控制[18-19]。
以上研究都是强调以移动机器人的运动学为基础构建运动控制器,即便运用了动力学模型,所设计的控制器都建模复杂, 计算量大。本文针对提高Mecanum轮全向移动机器人的路径跟踪效果,研究了Mecanum轮全向移动机器人的动力学模型,从原动力学方程出发建立特征模型,利用慢时变差分方程描述控制量与输出量的特征关系,降了模型的复杂性,提高了计算速度,易于运动控制器的设计[20],并设计了基于动力学特征建模的MPC轨迹跟踪控制器来提高全向移动机器人运动的精度和鲁棒性。
1 数学模型的建立
1.1 全向机器人的动力学分析
本文研究的是采用O-长方形的Mecanum轮分布结构的移动机器人,有4个交流伺服电机独立驱动,实际上是通过直接控制4个Mecanum轮的转动方向和速度,间接实现机器人在工作环境中的精确控制。如图1所示,以移动机器人的的几何中心建立坐标系(xy),1θ•、2θ•、3θ•、4θ•分别为4个Mecanum轮的转速,l1为机器人上下2个车轴距离的一半;l2为机器人两边车轮中心距离长度的1/2。Mecanum轮全向移动机器人具有3个方向的自由度,运用拉格朗日第二类方程从能量的角度分析系统的动力学,建立移动机器人的Lagrange函数。
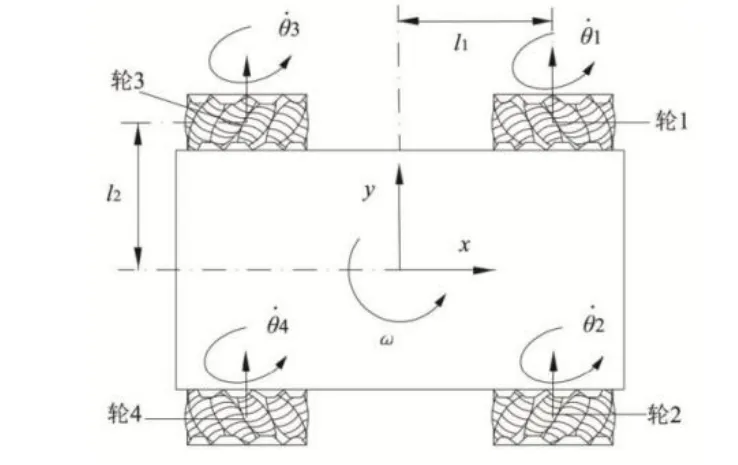
图1 Mecanum 四轮移动机器人


机器人行驶时,存在地面和空气等阻力,整个系统存在能量损耗,假设阻力系数为μ,则整个系统的瑞利耗散函数为

在势力和耗散力的作用下,拉格朗日第二类方程为

iQ为轮子的驱动力,将式(3)和式(4)代入式(1)可得:


1.2 特征建模
特征建模是根据机器人动力学特征、工作环境特征和控制特征相结合进行建模, 而不是单独的建立移动机器的高阶动力学模型,特征模型的形式比单纯的机器人动力学方程简单,便于实现运动控制器设计,它把移动机器人高阶复杂动力学模型的特征信息都转化为几个携带相关特征量的特征参数,新优化的特征模型不仅不会不丢失信息,而且降低了模型的阶数,一般情况下用慢时变差分方程描述特征模型用。在文献[21]中,对于如下形式的系统:





2 模型预测控制器的设计
2.1 MPC 模型预测
模型预测的原理是根据统当前的状态向量,结合期望的控制量建立一个短期时间内的数学预测模型,它可以对未来一段时间内的输出量进行预测,MPC算法包括预测模型,滚动优化,以及反馈校正3个要素。MPC预测控制器的原理见图2。

图2 控制器原理
2.2 确定预测模型
根据移动机器人动力学的特征模型,构建系统状态空间模型:


2.3 目标函数的设计
系统控制的目标是速度跟踪控制,针对机器人在移动时可能会出现强烈振动现象,需要对控制的输入量进行优化,将模型性能指的评价函数定义为

2.4 预测控制


依据实际情况对机器人状态、控制量及控制量增量设定上下限后,可以将多约束下的模型预测控制问题转换为一个标准的二次型规划问题:

以该控制量计算出当前系统的状态信息,且把这一时刻的状态信息做为新一轮模型预测的输入,通过系统的滚动优化会得到下一个时间点的控制增量,在这个MPC控制器中不断循环计算,直至实现所有的控制过程为止。
3 试验与结果分析
为了验证本文设计的基于运动学特征建模轨迹跟踪控制器的有效性,用Matlab仿真模拟移动机器人直线和圆型轨迹的跟踪效果,并与传统动力学建模设计的控制器做对比。取预测步长NP=40;控制步长NC=30;Q=50E,R=1E。
3.1 直线轨迹跟踪

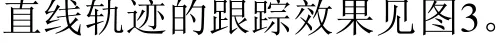
从图3(a)可看出,面对简单的直线轨迹时,采用特征建模的轨迹控制器和传统建模的轨迹控制器的跟踪效果都比较理想,即使存在初始误差也能快速拟合到理论轨迹上。图3(b)~图3(d)因为初始位姿在x轴上存在初始误差,所以2种轨迹控制器在速度v、x方向误差和y方向误差在初期存在一个较大的差距,后面又很快的稳定在一个定值,从变化曲线上看,特征建模控制器相对更稳定,误差变化小。
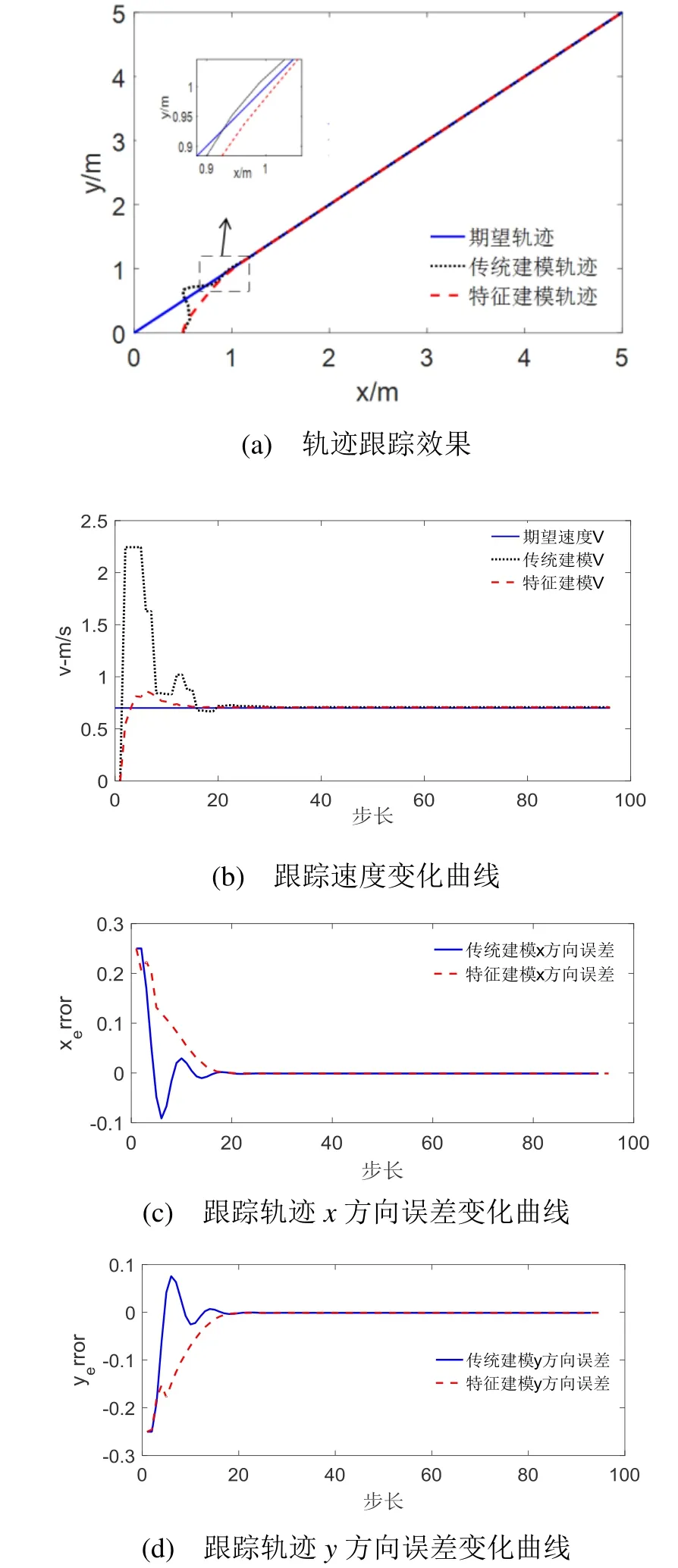
图3 直线轨迹跟踪效果
3.2 圆型轨迹跟踪
圆型的参考轨迹表达式为

期望参考速度为vr=0.64 m/s,机器人的初始位姿(0.2, 1.8, 0)。
圆形轨迹跟踪效果见图4。

图4 圆形轨迹跟踪效果

图4 圆形轨迹跟踪效果(续)
从图4(a)可看出,动力学特征建模的轨迹控制器在面对较复杂的圆型轨迹时,在初期因初始位置的原因轨迹会出现较小的抖动,但后期的跟踪效果比较理想。传统动力学建模的控制器初期轨迹的抖动相对较大,且跟踪效果没有特征建模控制器的精度高。图4(b)和图4(c)反映出2个控制器在前期x方向和y方向的跟踪速度都会出现突变和抖动,使用特征建模控制器的速度突变较小,抖动不明显;传统建模控制器的突变最大,前期速度抖动比较明显,2者速度都比较符合余弦函数的样条。图4(d)中的误差变化曲线再次证实了采用特征建模的控制器不仅前期轨迹抖动不明显,且跟踪的精度较高,系统控制器比较稳定。
4 结论
1)针对Mecanum轮全向移动机器人轨迹跟踪问题,利用特征建模理论对机器人动力学重新搭建特征模型,结合MPC算法设计一个基于特征建模的模型预测控制器。
2)对机器人动力学特征建模,简化了运动控制器的设计,仿真结果表明,采用特征建模的模型预测控制器具有较好的路径跟踪效果,相较于传统动力学建模控制器,特征建模控制器的跟踪误差更小、跟踪效果更好,跟踪速度突变较小,无明显的速度抖动现象,控制器更稳定。
