考虑不确定性的风力机翼型颤振边界研究
2022-08-17于佳鑫王晓东陈江涛吴晓军
于佳鑫, 王晓东, 陈江涛, 吴晓军, 康 顺
(1.电站能量传递转化与系统教育部重点实验室 (华北电力大学), 北京 102206;2.中国空气动力研究与发展中心, 四川 绵阳 621000)
0 引 言
当前风力机叶片的尺寸越来越大,2030年风轮直径有望达275 m[1],这必然会增加叶片的柔性。柔性叶片更易发生不稳定振荡。从经济性方面来看,颤振会导致叶片寿命降低,影响整个发电系统;从安全性角度来说,可能会引发叶片扭转受损甚至安全事故。因此,在设计叶片时则不得不考虑振荡的效应[2]。
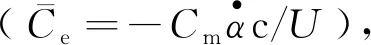
为了增加风力机叶片气弹性能,从气动性能角度出发,学者们对提高气动性能参数的鲁棒性做了很多研究[8, 9];从降低结构疲劳破坏的角度来看,学者们对提升结构材料性能[10]和结构布局[11,12]也做了一些分析,然而,实际环境中的不确定因素可能恰恰是引发叶片不稳定颤振的原因[13]。文献[14]表明气动力和结构特性的随机性影响着风力机叶片不稳定振荡的发生,且结构特性的随机性会降低颤振的临界速度。文献[15]分析叶片刚度、材料等结构不确定性对于叶片固有频率的影响。因此,在翼型及叶片的设计阶段就需要考虑不确定因素对其稳定状态的影响。
文献[16]用蒙特卡洛方法(MC)研究风力机叶片的随机振荡问题,分析了颤振发生的概率及临界失效点,然而,MC方法效率很低,计算量巨大。基于谱分析的多项式混沌法效率高,通过与CFD进行非嵌入式耦合,已经被广泛应用于随机气动问题的求解[17]。文献[18]采用基于稀疏网格的多项式混沌法(SGPC)对多维随机几何进行气动不确定性分析,相较于概率配置点法[19]在变量维数较多时计算量指数增加的情况,基于稀疏网格的多项式混沌法在保持结果精度的同时,计算效率也取得了显著的提高。
因此本文针对翼型的俯仰沉浮耦合振荡形式,采用能量法对颤振边界进行研究与分析。探究翼型运行过程中诱导不稳定颤振的主要不确定因素,并基于SGPC的不确定性分析方法量化它们的影响程度。
1 数值方法
1.1 几何模型
DTU 10 MW风力机叶片的气动外形使用FFA-W3翼型族设计,该翼型族由瑞典航空研究院设计,包含7种翼型,厚度范围为19.5%~36%,是非常有代表性的风力机专用翼型。DTU 10 MW风力机风轮直径达到178.3 m,单只叶片长86.466 m。在复杂的风况下,叶片柔性大,导致叶尖位移较大,有很大可能面临颤振风险的可能。FFA-W3-241翼型的相对厚度小,升阻比高,被用于DTU 10 MW风力机叶尖位置的气动外形设计。因此本文选用FFA-W3-241翼型进行研究,其几何外形如图1所示。

图1 FFA-W3-241翼型几何外形图
1.2 计算域与网格
本文中CFD模拟采用嵌套网格方法。嵌套网格由两套网格构成,分别是背景网格和贴体网格。背景网格保证远场的计算,贴体网格随翼型共同运动,确保翼型周围的网格质量。背景网格的计算域为正方形,各边长度为40倍弦长(40c);翼型旋转轴位于正方形中心,各边距离旋转轴20c;贴体网格所在的区域为距离翼型旋转轴3c的圆形。
为保证翼型壁面的计算精度,贴体网格包含了15层边界层网格,膨胀率为1.2;边界层外侧膨胀率为1.5,并保证壁面网格y+<1;翼型上下表面各200个节点,FFA-W3-241翼型为钝尾缘,尾缘设置50个节点。背景网格的各边长的网格节点数为150,等距分布。贴体网格总数为50 958,背景网格总数为22 201,背景网格和贴体网格如图2所示。
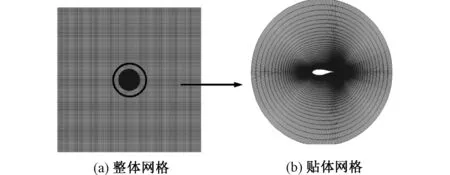
图2 计算域网格
1.3 边界条件
根据风洞试验条件[20],CFD数值模拟采用的雷诺数为160万,湍流强度为1.0%,左侧边界为速度入口,翼型表面设置为光滑的无滑移壁面,上下边界为了实现平行流动,速度和压力的边界条件设置为零压力梯度。计算域和边界条件如图3所示。求解器采用开源的OpenFOAM求解器。湍流模型采用k-ω SST模型。
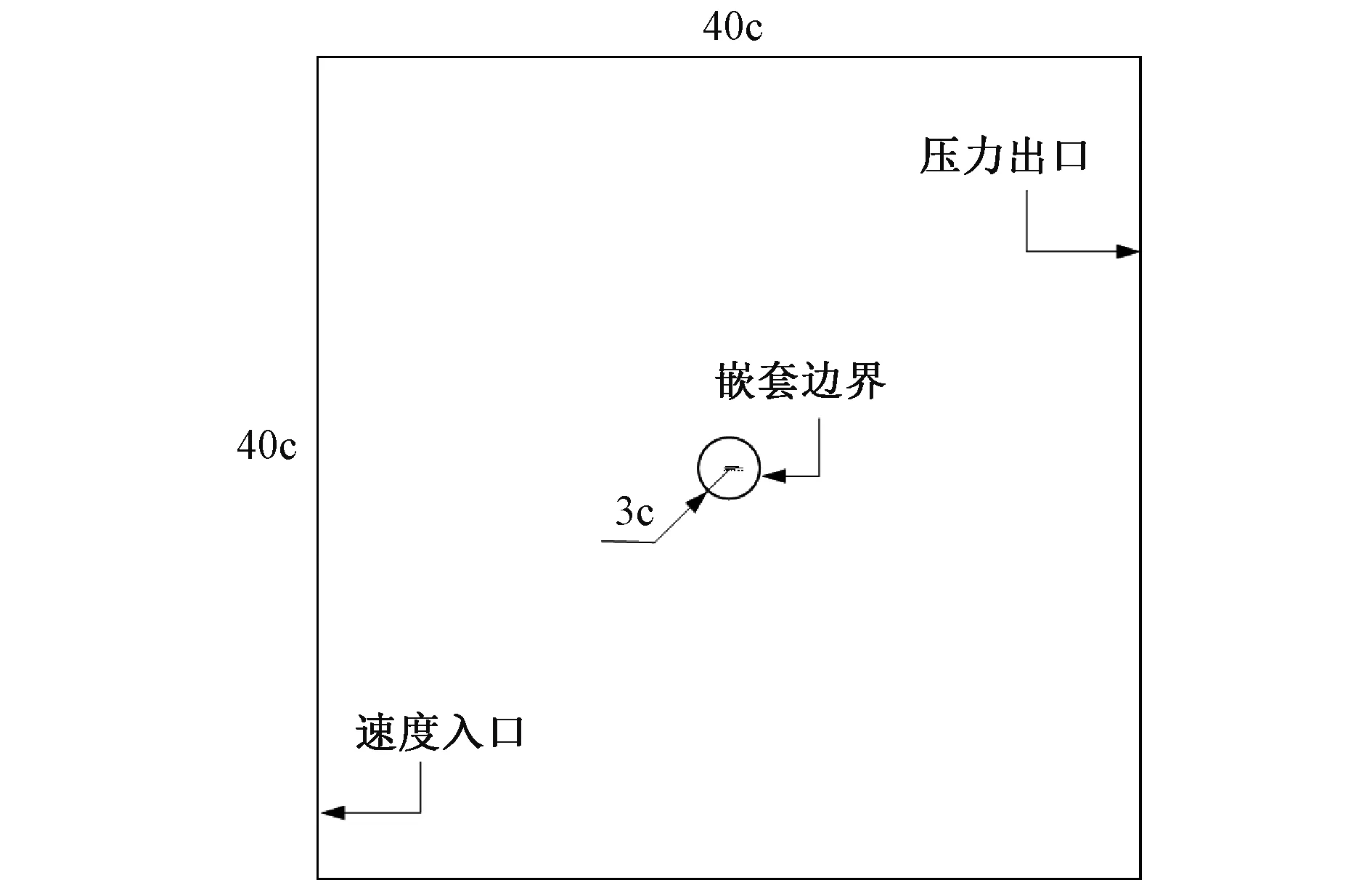
图3 计算域及边界条件
2 数值方法确认
2.1 动态时间步长、计算周期验证
对于非定常计算,时间步长对计算结果和计算成本影响较大。较小的时间步长能精确的描述物理现象,但是增加了计算成本。因此,为了得到精确的物理现象和较低的计算成本,进行了俯仰振荡的时间步长验证。俯仰振荡的攻角变化为α=αmea+αamp·sin(ωt)。以平均攻角αmea为15.6°,振荡幅值αamp为1.8°为例,在一个振荡周期内设计了4种时间步长,分别是一个周期内计算360、720、1 080和1 440步。俯仰振荡的折合频率为0.093,折合频率定义为
(1)
式中:f为振荡频率;c为弦长;U∞为自由来流速度;ω为角速度。
图4展示了第1~5个周期内各时间步长的升力系数时间历程,其中第1个周期内的结果未收敛,未在图中展示。一个周期内,采用360和720步的结果与采用1 080和1 440步的结果相差较大1 080和1 440步的结果几乎重合,达到收敛。同时可以看出,采用720步长时,3个周期后的结果达到收敛。
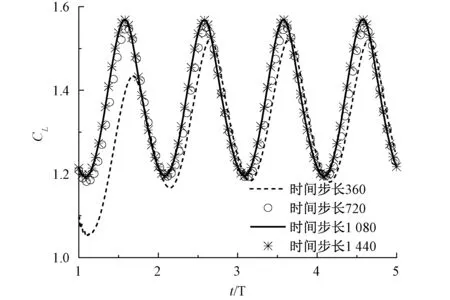
图4 升力系数的收敛历史
2.2 数值验证
图5展示了未失速、轻度失速和深度失速三种情况下的升力系数曲线,并与文献[20]中的实验结果进行对比。可以看出,稳态计算时,附着流区域计算值与实验吻合较好,然而在失速区内,模拟结果对分离点的预估相比于实验稍有推迟,升力系数计算结果偏高于实验值。这是由于RANS对于分离涡的捕捉不够精准。在瞬态计算中,附着流区稳态增长斜率较大,迟滞回环的斜率也较大。失速区内,静态升力系数曲线穿过动态迟滞回环,攻角15°时稳态计算值与实验值偏差相对较大,20°后差距逐渐减小,因此瞬态计算中,15°附近的迟滞回环计算偏大,20°附近差距减小。动态计算的误差在可以接受的范围内。
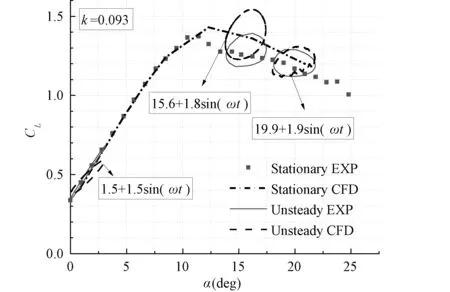
图5 三种工况下的升力系数曲线
3 两自由度耦合振荡结果分析
翼型的俯仰振荡和沉浮振荡分别对应了叶片的挥舞与扭振,运动方程如下式。
α=αmea+αamp·sin(ωt)
(2)
h=H·cos(ωt)
(3)
由于翼型运动导致的弦线方向时刻改变,与来流方向夹角也时刻改变,因此存在实际等效攻角。根据文献[21],俯仰沉浮耦合振荡时流场的有效攻角为式(4):
(4)
3.1 轻度失速颤振边界
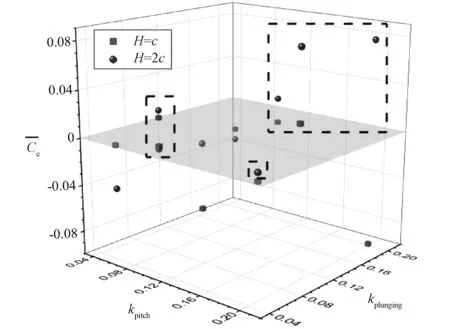
图6 不同沉浮幅值下净能量传递系数随俯仰、沉浮折合频率的变化(αmea=15°,αamp=4°)
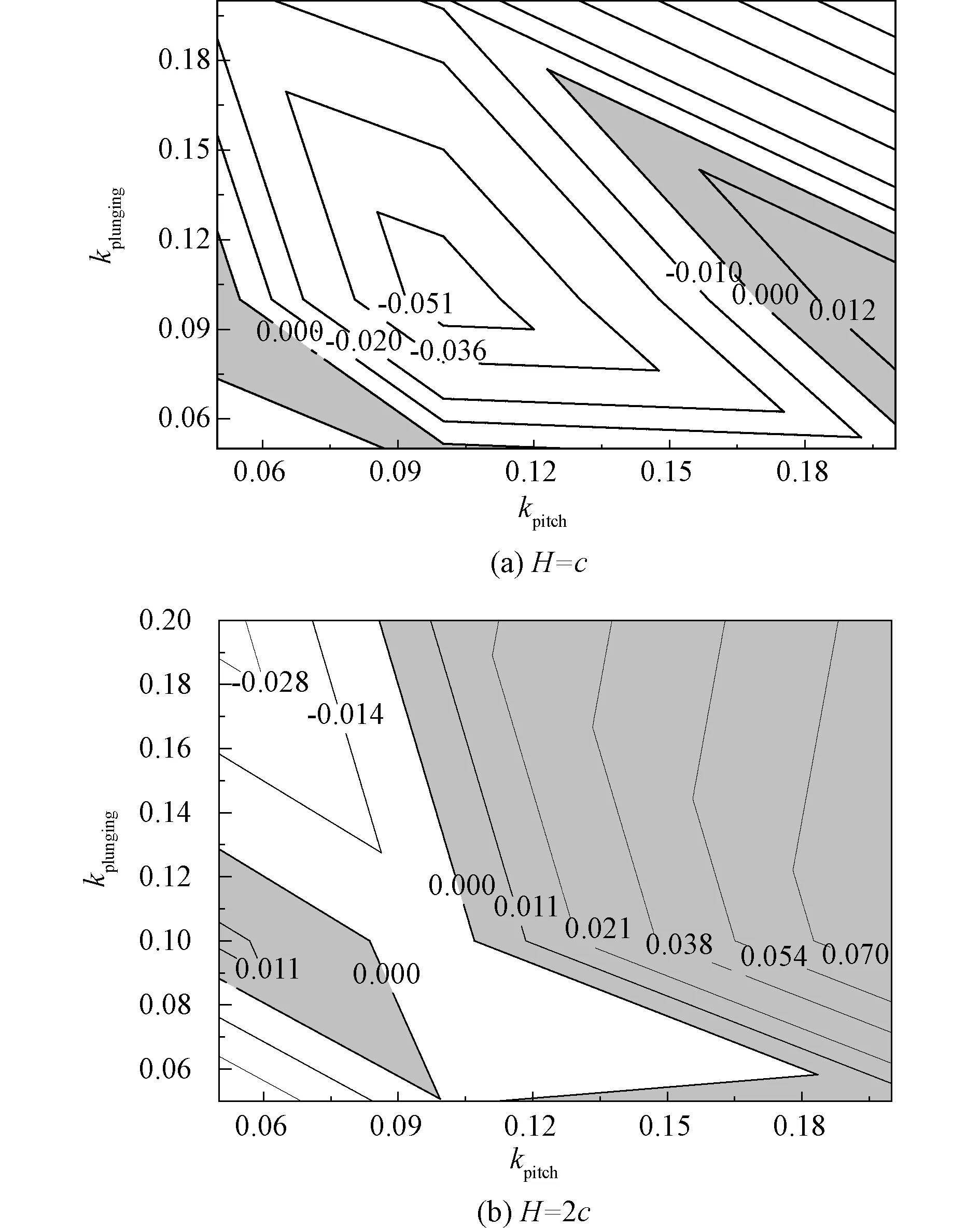
图7 净能量传递系数等值线云图(αmea=15°,αamp=4°)
3.2 深度失速颤振边界
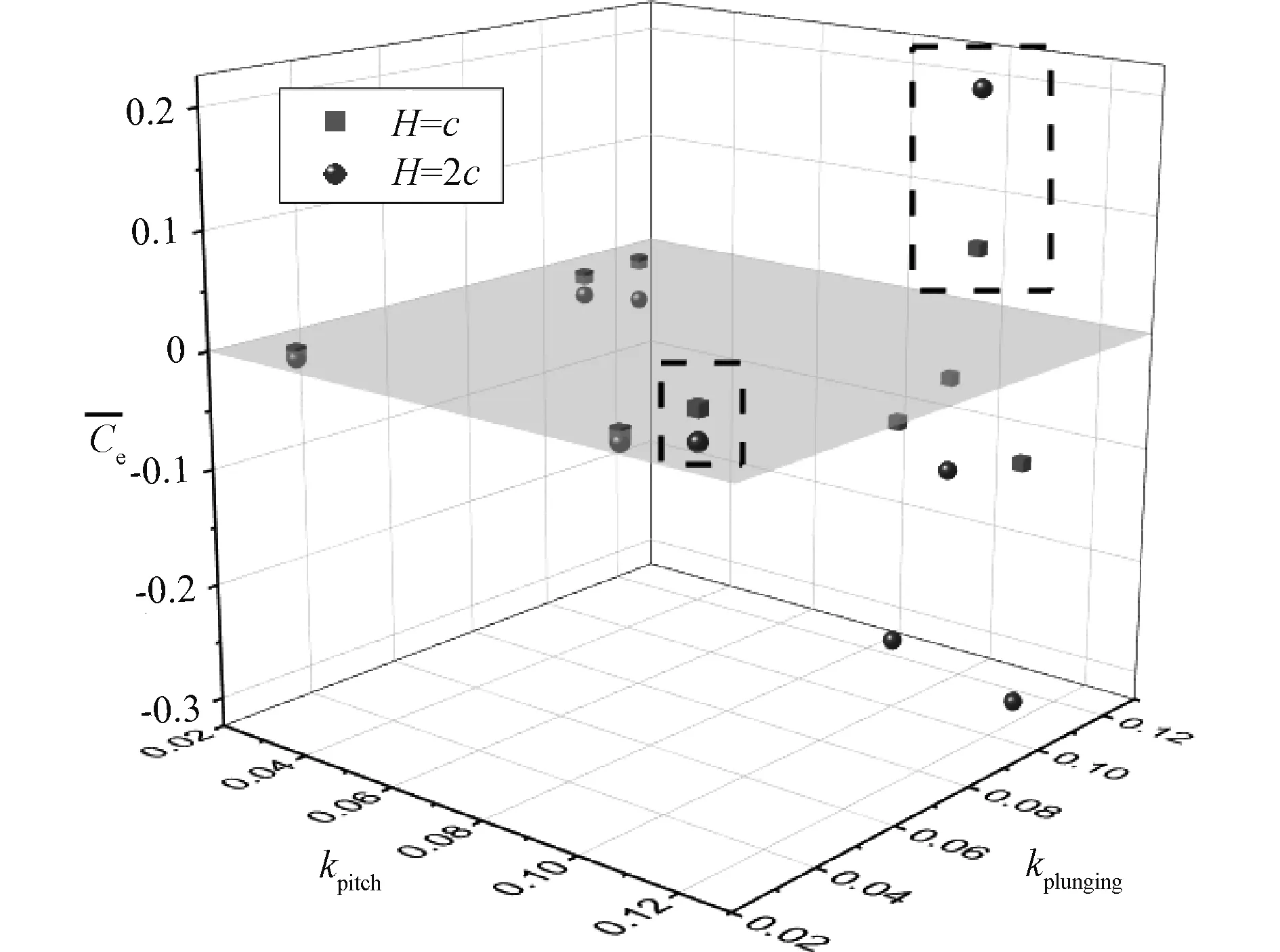
图8 不同沉浮幅值下净能量传递系数随俯仰、沉浮折合频率的变化(αmea=18°,αamp=4°)
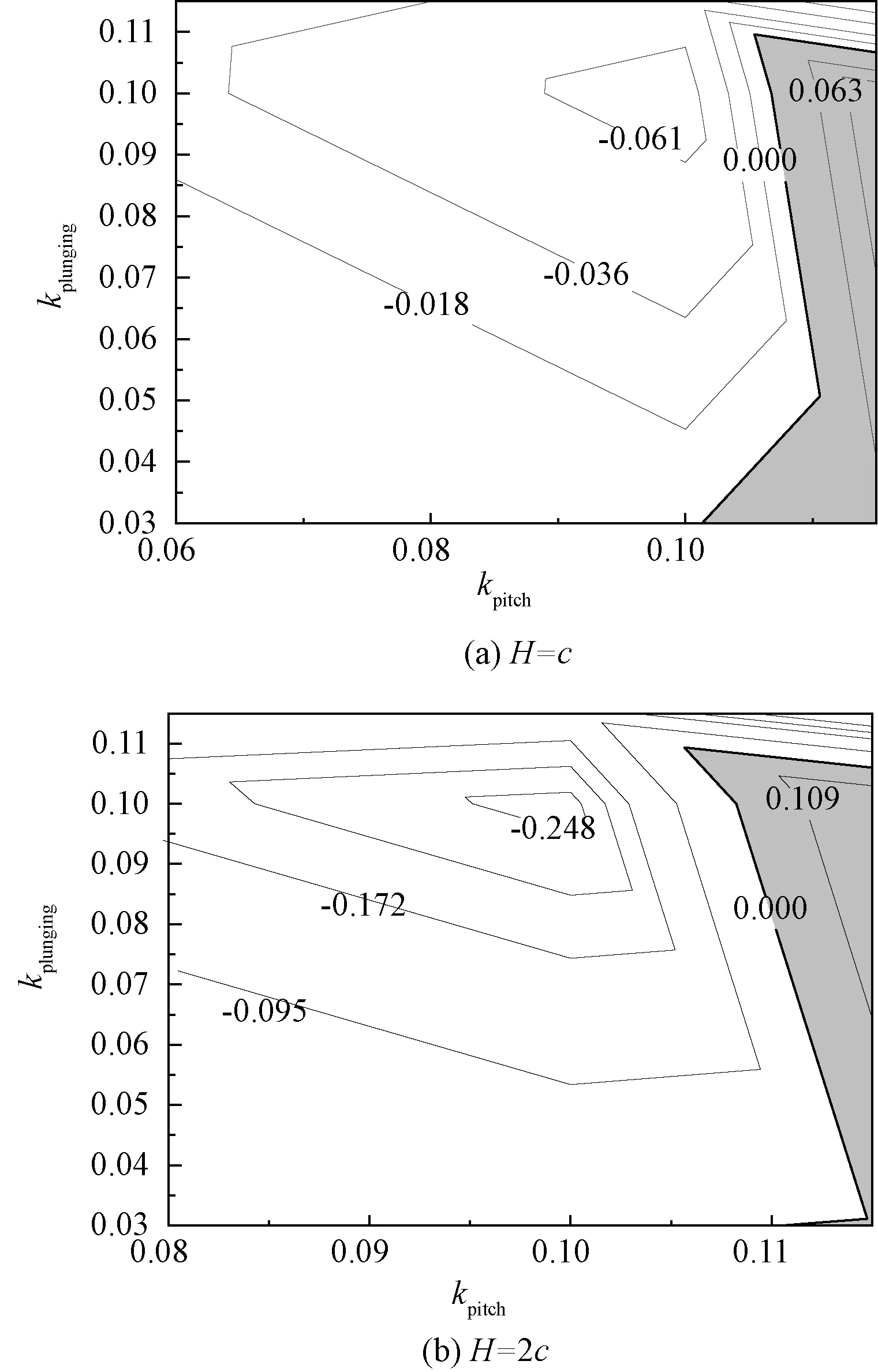
图9 净能量传递系数等值线云图(αmea=18°,αamp=4°)
3.3 轻度失速的不确定性分析
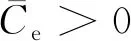
采用能量法分析颤振的稳定性,由于能量法没有考虑流固互相作用的过程,预先给定了振动的振幅和振型。而在真实工作环境下,存在来流风速、几何误差等不确定性因素,使得失速颤振时振幅和振型不断变化。由于3.1节中轻度失速的颤振边界不明确,综合不确定性因素影响,本节将振幅和振型作为不确定性量,对轻度失速的颤振发生进行不确定性CFD数值模拟与分析。深度失速由于颤振边界明确,将不再作不确定性讨论。
考虑了俯仰平均攻角、俯仰攻角振幅、俯仰折合频率、沉浮距离振幅、沉浮折合频率五个不确定因素。假设这些不确定变量服从高斯分布,均值及标准差见表1。采用稀疏网格法构造多项式混沌,对应61个不确定工况。基于稀疏网格的多项式混沌方法参见文献[18]。
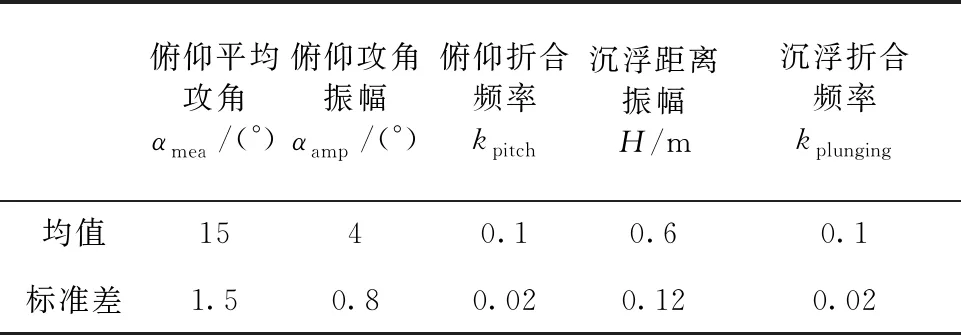
表1 不确定变量均值及标准差
敏感度分析采用的是文献[22]的整体敏感性指数。图11计算了5种不确定因素对净能量传递系数的灵敏度指数,发现影响最大的因素是俯仰频率,而不是本征值较大的攻角,其次影响较大的是沉浮频率,沉浮距离、攻角均值及振幅对颤振的敏感度不高。
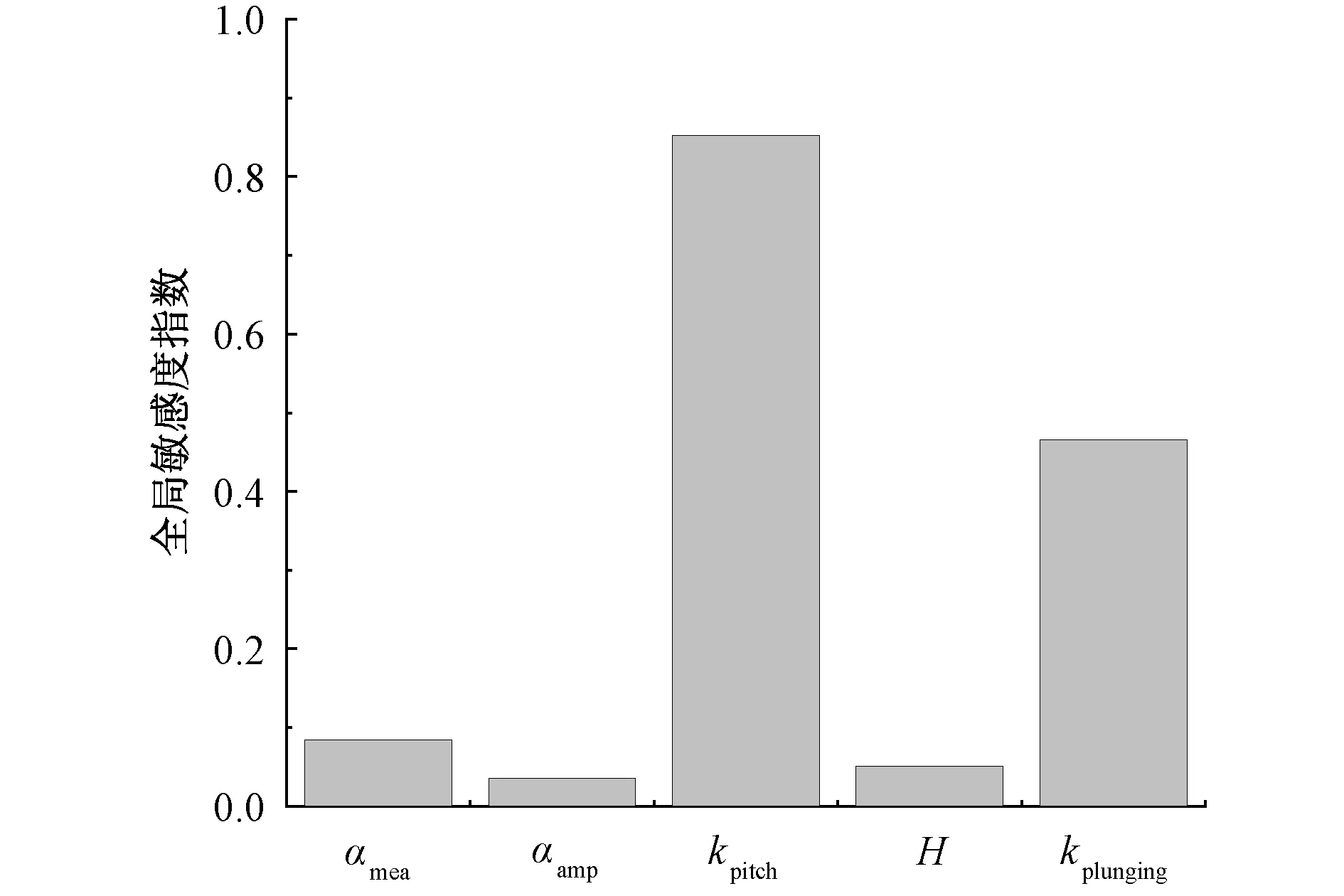
图11 敏感性分析
4 结 论
本文采用CFD模拟对FFA-W3-214翼型进行了俯仰与沉浮耦合运动的数值计算,并用能量法找寻了轻度失速和深度失速工况下的颤振边界,得出如下结论:
(1)对于轻度失速,当沉浮距离幅值为一倍弦长时,在低折合频率下有颤振发生,但边界不明显。当沉浮距离增大至两倍弦长,随折合频率的增加,颤振现象更加明显;
(2)在深度失速工况下,颤振现象较轻度失速更明确,可找出明确的颤振边界。且沉浮振幅增大使颤振边界中俯仰折合频率范围减小,沉浮折合频率范围无明显影响;
(3)通过对颤振边界不明确的轻度失速工况运动参数的不确定量化分析,可以预测该工况下颤振发生的概率达49.48%。此外,运动参数中对颤振影响最大的因素是俯仰折合频率,其次是沉浮折合频率,沉浮距离、攻角均值及振幅对颤振的敏感度不高。
