基于成像光谱的温度场重建
2022-08-17洪途赵猛秦天令蔡红星
洪途, 赵猛, 秦天令, 蔡红星
(1.长春理工大学 物理学院, 吉林 长春 130022; 2.北京理工大学 光电学院, 北京 100081)
在研究爆炸燃烧过程中,针对温度场这一描述火焰重要基本参量的测量具有诸多现实意义[1]。而当前业界许多测温技术[2-4]仍然停留在单点或有限多点测量阶段,如红外热像仪虽可以快速测得固体目标的温度分布图像,但是对高温低密度的火焰气体团却束手无策。同时传统光纤光谱仪仅可单点或逐行测量有限点位的光谱以反演温度,这已难以满足当前实际需求。
在不破坏当前被测温物体的前提下,能够实现对瞬时火焰温度分布的准确实时测量已经成为亟需解决的关键技术。目前,在多光谱辐射测温研究领域已有许多相关研究工作,这些研究大致可分为2类,即接触式测温和非接触式测温。接触式测温包括热电偶以及光纤测温,由于受到传感器热惯性的影响和传感器本身材质的限制,接触式测温无法用于反映瞬态爆炸过程的温度变化。而非接触式测温包括声波法、辐射法、激光光谱以及成像法等。文献[5]提出了一种红外发射计算机层析成像方法,通过计算火焰发射的红外辐射强度作为投影数据来测量火焰任意跨轴层的温度分布。文献[6]提出了一种用于反演任意浓度场和温度场的多角度扫描吸收测量方法,分析了模拟误差和累积反演误差对求解精度的影响。文献[7]讨论了具有一定分辨率的高速高温计的一般设计准则,并根据被测对象的温度与时间特性分析了多种参数对高温计性能的影响。文献[8]设计了一种三色比高温计,以获得燃烧碳质颗粒的表面温度和高温燃烧速率。随后将该仪器特性及性能与先前类似研究中构建的双色比高温计进行比较,并展开讨论。在文献[9]中,研究者提出了一种基于神经网络对数据处理的黑体炉及光学过滤器,并与已知光谱透射率曲线结合用于工程材料温度的测量。该方法被验证是解决真实温度和发射率测量问题的一种有效方法,它可以克服发射率和波长之间假设对于大多数工程材料真实温度和光谱发射率测量的影响。文献[10]研究了一种基于遗传算法和人工神经网络的温度测量方法用以实现基于亮度温度的多光谱测温过程中的数据处理。其实验验证结果表明,与单纯基于人工神经网络的测温方法相比,引入遗传算法后能够得到更高精度的测温结果,这在业界研究与应用中具有重要意义。综上,虽然现有的非接触式多光谱辐射测温法已经相对成熟,但是所做研究工作在火焰温度场测量的实时性及准确率等方面仍存在一定程度上的不足。
本文基于八谱段MSFA成像系统[11]提出一种基于多光谱相机拍照成像光谱的多光谱相机辐射测温技术,以实现瞬时火焰温度场的测量。首先针对所要测量的火焰光谱数据进行采集,并利用高温黑体及太阳光谱对集成硅基芯片的光谱相机进行标定,解算光谱修正函数;在对光谱进行预处理后,基于二叉树结构思想设计重复阵列等空间概率比八谱段MSFA光谱成像结构;随后根据所收集光谱数据设计一种基于邻域图像梯度延伸的光谱图像重建方法以实现更高精度的温度测量;最后,由普朗克定律出发构建集成硅基芯片的光谱相机测温模型,以实现温度反演过程,从而实现瞬时温度场的准确测量。
1 测温原理
以往许多相关测温研究工作都是使用单波长高温计测量得到对应的高亮温度值以及利用全波长辐射温度得到其对应辐射温度值等[12],而其中许多工作都是基于检定常数数学模型来实现辐射温度判定[13]。这种方法既能够求取不同波长条件下的光谱发射效率,同时也可以实现目标物体真实温度的准确测量。
本文将利用国家标准黑体炉实现辅助标定,使得可以在不计检定常数所带来的误差的情况下求得更加精确的目标标准温度T以及光谱发射效率φ。根据马克思·普朗克经典黑体辐射定律,任何温度超过绝对零度的客观物体向外辐射能量的能力是随着温度的升高而逐渐增强的,即温度越高的物体有能力辐射出越多能量。黑体能够将辐射至其表面的能量全部吸收且不反弹不透射,能够在相应温度情况下实现最大辐射能的释放。这里普朗克定律可以描述理想状态下辐射现象:
式中:Eb表示当波长为λ的情况下单位波长所对应的光谱辐射强度大小,W/(m2·μm);c1、c2分别表示普朗克第一、第二辐射常数,且c1=3.743×10-4W·μm2,c2=1.439×104μm ·K;λ为当前辐射波长,μm;T为黑体绝对温度,K。由此可见,根据普朗克定律即可在已知某波长及其辐射强度的前提下计算黑体绝对温度T。
一般情况下,若多波长温度计具有n个通道,为了便于处理,可以根据维恩公式实现下一步操作以完成测温过程。第i个通道的输出信号Si可以被表示为:
式中:c1、c2为经验常数;T为平衡时的温度;Aλi为当前物理通道中所参照的物理参数,此物理参数仅与波长相关且与当前温度不相关。同时Aλi与当前波长条件下探测器对应参数相关,即它与此探测器当前所对应的光谱响应效率、几何尺寸、光学元件透过率以及第一辐射常数等物理因素是相关的。
2 测温结构系统设计
本文在当前可见光谱的基础上引入高斯函数来对八谱段滤光片中光谱敏感性函数(spectral sensitivity functions,SSF)曲线[14-15]进行仿真拟合,由此可定义滤光片SSF透射函数T(λ)为:
式中:ρ为当前状态下波长的标准差;θ为当前所采数据样本中中心波段均值或期望值的大小。各个成像谱段的SSF曲线可以根据对当前参数ρ与θ的筛选来有效调整。本文所用MSFA滤光片阵列分布如图1所示。

图1 八谱段滤光片分布结构Fig.1 Distribution structure of eight-band filter
本文所用的八谱段在当前滤光片阵列的空间分布规则基于文献[16]中研究工作。在整个工作过程中,要最大程度地保证光谱图像重建的精度,保证某一光谱波段敏感像素区域具有与其他相邻区域相同的特性并尽量降低其变化幅度。同时,在此过程中,每个像素仅占有单个来自于对特定光谱波段直接测量结果,而未被测量的光谱像素点要根据相邻图像区域成分来进行估计。这就要求每个光谱波段滤波器阵列能够对整个光谱图像进行均匀采样。否则若像素在某些区域分布密集而在其他部分分布稀疏则会导致光谱信息严重丢失从而影响整体测量的精确度。所以,为了保证均匀的空间采样率,在本文中采用基于二叉树生成法的MSFA光谱段空间概率分解方案[17]来实现二进制分裂迭代操作过程,以实现空间采样率均为1/8,从而降低非均匀分布所导致精度降低的概率。
3 温度场重建算法的实现
针对当前基于光谱重构的温度反演研究中存在的问题,本文提出基于多光谱相机拍照成像光谱的多光谱相机辐射测温技术,以实现瞬时火焰温度场的重建。首先本文针对所要测量的火焰对象进行光谱数据的采集,随后对所采集的光谱数据进行预处理以提高测量精度。在对所得到光谱数据进行去背景与修正之后,本文采用八谱段MSFA光谱Raw图像重建方法实现光谱重建,随后基于普朗克定律出发构建集成硅基芯片的光谱相机测温模型以实现温度反演操作,完成对瞬时温度场的测量。同时,本文利用高温黑体及太阳光谱对集成硅基芯片的光谱相机进行标定,用于解算光谱修正函数进而提高测量精度。
3.1 光谱数据预处理
利用数据预处理来克服可见光光谱分析中由于样品粒度、仪器背景及其他相关因素所导致基线倾斜以及漂移问题,从而提高模型准确度以及鲁棒性等。
在本文所采集光谱图像的分析及研究中经常会因为火焰间存在干扰信息等导致光谱谱线产生重叠等现象,可采取导数算法[18]进行处理:
接下来,进行多元散射校正过程。为了取得标准光谱即平均光谱,本文对所取得的各位置光谱进行平均化处理。随即将每个位置上的光谱数据与平均光谱进行一元线性回归操作以求得其回归系数及回归常数。最后,为了使修正光谱基线相对倾斜,再将各初始光谱回归常数做相减并除以其回归系数。
本文利用Savitzky-Golay(S-G)方法对光谱数据进行平滑滤波,使得原始光谱的平滑性得到显著提高并实现噪声干扰的有效降低。与此同时,将光谱矩阵中行数矩阵做标准正态变换,即标准归一化,以实现各光谱数据点吸收光度值服从正态分布。
3.2 光谱Raw图像重建及温度场反演过程
为了实现对原始光谱图像的结构特征以及纹理信息的较好保留及还原,本文采用一种八谱段图像重建方法[19],将邻域采样点所包含的图像梯度相关参数扩展至光谱图像中未进行采样的点。设未被采样光谱图像点所在位置为b,其对应邻域中所包含采样点为a,基于将已知梯度信息由a点扩展至b点这一前提,本文利用taylor polynomial estimation方法对未采样点进行估计:
f(b)=f(a)+f′(a)(b-a)+…+
式中:fn(x)为当前函数表达式的n阶导数;Rn(x)为拉格朗日型余项。
针对本文中所研究的二维光谱图像,可以利用已被采样的光谱图像点的梯度相关信息进行图像重建。将a至b的方向向量定义为:
式中:ab表示a与b在当前二维空间中的距离值大小。由此可以得到其方向导数为:
由此,可以根据方向导数及梯度在已知a的情况下对b进行估计:
如图2所示,可以根据已知采样点a来对其邻域中未采样点b进行重建。此时重建未被采样点b的过程可表示为:
式中:ai∈Ws为光谱图像中窗口Ws内已采样点;Mai为未采样点ai所在位置的二进制掩码且Mai∈{0,1};ωai为ai所在位置的核权重值;Cai(b)为从ai到b的贡献值。其中核权重ωai可表示为:
由于本文旨在二维光谱图像重建,所以这里选取几何距离作为权重来进行计算,即采样点ai距离未被采样点b越近则关联度越大,反之则关联度减小。基于以上操作过程可根据当前谱段排列特性实现光谱图像重建。针对临近b点的未采样点进行估计。
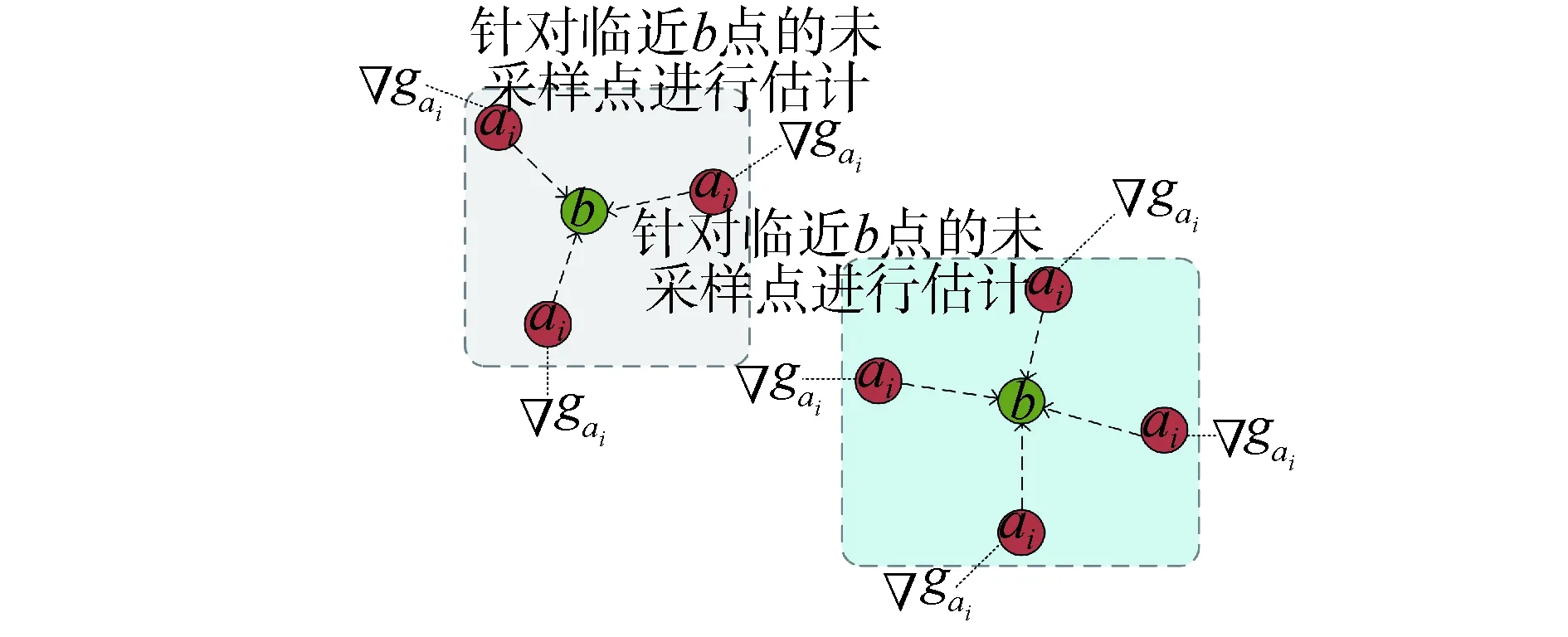
图2 利用邻点对未被采样点进行估计Fig.2 Using adjacent points to estimate the non-sampled points
针对温度场测温过程,本文通过光谱相机采集待检测目标的辐射光谱数据,随后在待处理特征光谱信号中提取作为下一步处理的数据集合。由光纤接收靶面接收后传送至信号采集处理系统中的光电探测器靶面[20]。光电探测器可将与光能相对应的电流信号输出并将其做去噪声整合等处理,最终传送至计算机采集模块,由测温软件及模型进行温度测算,以实现温度测量的目的。
3.3 定标过程
本文中采用一点标定法[21]实现一种基于波长函数的标定工作。在对光纤光谱仪波长函数进行精确测定操作后,利用黑体炉进行标定实验过程。其中,黑体炉工作温度范围为600~1 500 ℃。当黑体炉温度为T时,可对一点进行标定得到结果Q。本文选择8个波长进行标定实验,最终标定6个温度点,反演误差小于0.03%,光谱仪反演黑体炉温度具有较高可信度,可以作为火焰温度测量的参考方法。具体结果如表1所示。

表1 基于黑体炉的光纤光谱仪标定结果Table 1 Calibration results of optical fiber spectrometer based on blackbody furnace
4 实验与分析
为了对本文所提出温度场重建方法的有效性进行实验验证,本文针对待测火焰本身向外辐射能量,当其通过不同中心波长的滤光片后,可被光学系统捕捉形成图像信号,从而得到特定波长下的火焰辐射信息,并将所得信号传入计算机,经过标定和计算,即可得出待测火焰的温度分布。同时利用国家标准仪器光纤光谱仪直接测量火焰光谱,进行温度反演得到火焰实际温度数据集合,以备验证光谱相机温度场重建方法的测温能力及准确程度。
4.1 实验过程
1)实验仪器:光谱芯片相机,具体参数如表2所示,帧率由图像传感器帧率上限决定,30帧/s,空间分辨率为640×480,30万像素;光纤光谱仪、酒精喷灯、实验用暗室等,如图3所示;
2)实验样本:酒精喷灯实际火焰温度场;
3)光谱采集:通过对光路的调节实现实验过程中所有器件同轴同高,同时保证光谱相机探测点所在位置是喷灯火焰轴对称方向的对称轴。随后利用光谱相机对光谱数据进行热噪声减弱处理,点燃酒精喷灯后,利用光谱相机对当前火焰进行拍摄以抓取火焰光谱图像,供计算机采集及测温模块使用。同时,利用经由黑体炉定标的光谱仪光纤探头进行光谱数据采集,并做温度反演,以验证光谱相机所反演温度的准确度,并确定其误差。
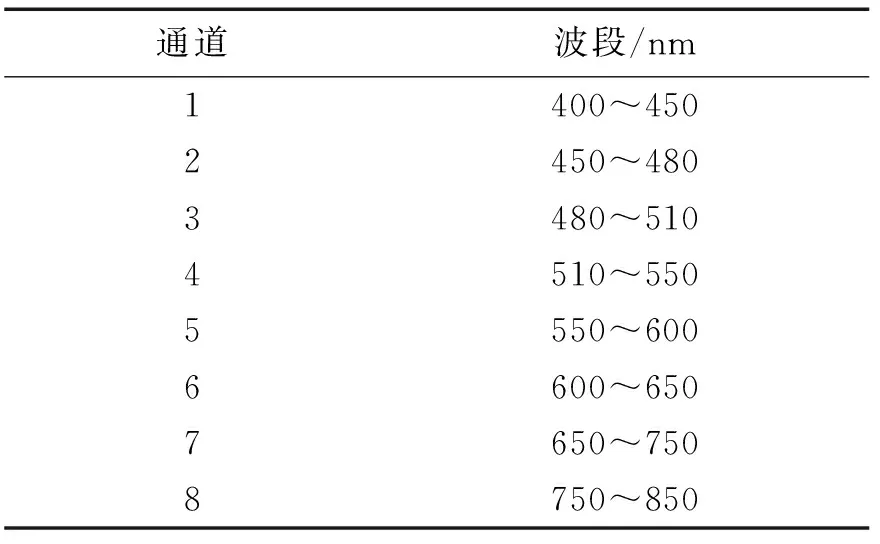
表2 光谱芯片相机的具体参数Table 2 Specific parameters of the spectroscopic chip camera

图3 实验环境Fig.3 Experimental environment
4.2 基于成像光谱的温度场重建测试
本文实验过程中所抓取的是一个140×42大小的喷灯光谱图像,如图4曝光区域所示,其对应八通道不同谱段图像如图5所示。当喷灯工作时,利用本文设计的测温模型系统采集其发出的光信号并对其对应温度进行测算。本文中选取61.20、47.34、38.51和16.30 mm这4个火焰高度对应温度点来对多光谱条件下辐射温度测试进行多次实验对比。根据采集到的多通道的光强度大小等参数,本文计算得到针对整个火焰光谱中测温点的平均测温情况如表3所示。

图4 光谱相机Raw光谱图像Fig.4 Raw image of spectral camera

图5 光谱相机八通道光谱图像Fig.5 Spectral camera eight-channel spectral image

表3 酒精喷灯测试光谱仪反演温度A与光谱相机反演测量温度B在各测温点的比较结果Table 3 Comparison result of the inverted temperature A by the alcohol blowtorch test spectrometer and the inverted temperature B measured by the spectrum camera at each temperature measurement point
由以上实验结果可以看出,火焰中心温度与其中心高度密切相关,随着火焰中心高度增加其火焰中心温度增高随后又随其高度增加而下降。同时可以发现其反演温度与真实温度比较接近。当火焰高度为38.51 mm时,火焰中心温度最高。从相对测温误差上来看,与光谱仪反演测温结果相比,本方法测得温度的误差总体上低于0.6%,表明本文提出的基于多光谱相机成像测温方法可以实现火焰温度场相对准确测量重建。除此之外,基于现有处理器条件下(i7-4710hq),本方法可以做到1帧/s的温度场重建,可以实现在较短时间内对火焰温度场的总体还原,弥补了传统辐射测温时采用单点或某几个点测量所产生的限制。
4.3 温度场重建方法性能对比
本组实验中,将多种温度场重建算法与本文所提出方法进行性能对比,其中包括同步迭代代数重构(simultaneous iterative reconstruction technique,SIRT)算法、总变分最小化(total variation minimization,TVM)算法以及离散代数重构(discrete algebraic reconstruction technique,DART)算法。在这里分别取20×20、30×30和40×40重建点数且重建方向是沿直角坐标两正交方向。沿不同高度针对4种温度场重建方法通过10组重复实验所测量测温点平均结果如图6所示。
从图6结果可以发现,本文所提出的重建方法相比于其他3种重建方法可取得更低的平均误差,能够对温度场较高精度的还原。在相对火焰高度为35.18、38.51以及47.34 mm的情况下,与其他3种重建方法相比,本文所提出重建方法能够取得低于0.7%的平均误差值,表明其在温度场重建过程中具备一定的准确性及稳定性,可为温度场快速重建提供良好基础。
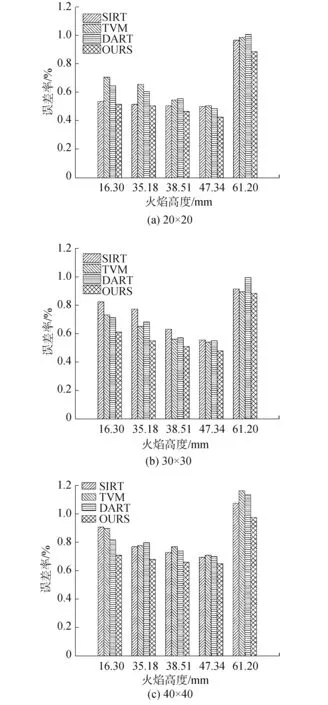
图6 重建方法性能对比Fig.6 Performance comparison of reconstruction methods
5 结论
1)本文针对当前瞬时火焰温度场测量问题,提出了基于多光谱相机成像光谱的多光谱相机辐射测温方法;
2)该方法利用八谱段MSFA光谱图像重建方法进行光谱重建并利用集成硅基芯片光谱相机测温模型实现温度反演;
3)实验结果表明,相比于当前多种温度场重建算法,本文所提出的基于多光谱相机成像光谱的多光谱相机辐射测温方法能够在保证温度反演准确程度的前提下实现较高的稳定性,同时能够较好地反映实际火焰真实温度分布情况。
