波流相互作用下潮流能无轴轮缘导管涡轮机水动力特性与尾流结构分析

宋 科， 杨邦成

（1.昆明学院 机电工程学院， 云南 昆明 650214； 2.昆明理工大学 建筑工程学院， 云南 昆明 650500）

0 引言

近年来， 随着各国对环境问题的愈加关注以及对碳排放实施更为严格的管控， 促使能源结构加快向绿色低碳型转型， 特别是向高比例的清洁可再生能源转型。 能源结构的转型不仅可以改善环境质量、应对气候变化，还可以培育新的经济增长点，实现经济社会可持续发展。作为一种可再生能源， 潮流能具有丰富的储备资源和较高的可预测性，在过去十年中，利用潮流能进行发电的相关技术得到了长足的进步与发展[1]。 目前，潮流能发电技术主要分为涡轮系统和非涡轮系统（振荡水翼、振荡转子等技术）两种。其中，涡轮系统在性能和可靠性方面具有较好的水平[2]，目前，全球部署了许多两叶或三叶的水平轴涡轮机系统[3]。 此外，为了提升潮流能涡轮机的行业竞争力与吸引力，有学者提出了带导管的涡轮机系统以提高其能量获取效率。 王树杰[4]研究了导管形状对涡轮机的水动力学性能的影响， 发现导管参数对涡轮机的能量获取性能有很大的影响。 Belloniet S K[5]使用RANS-BEMT 模型分析了导管涡轮机的水动力学性能。 宋科[6]从多个方面对一种薄壁导管涡轮机的水动力学性能进行了分析。 刘清照[7]研究了导管安装角度对涡轮机水动力性能的影响。 Tampier G[8]对导管涡轮机的水动力损失因子进行了计算和研究。 程帅兵[9]研究了导管间距对涡轮机水动力性能的影响。

现阶段， 导管涡轮机技术已经具备一定的商业化运作氛围， 并在一些沿海国家实现了并网发电。尽管该技术为行业领域开辟了新的方向，实现了潮流能的高效利用，但同时也存在一些问题，如导管涡轮机需要一定的轴系支撑结构来保证叶轮、电机与外部导管的匹配定位，而轴系支撑结构的存在必然会造成一定的流动干扰与阻力， 从而影响导管涡轮机系统的运行稳定性。 为了解决该问题， 笔者提出一种新概念导管涡轮机系统-无轴轮缘导管涡轮机。 这种导管涡轮机系统去除了传统的轴系支撑结构， 将发电机系统内置安装在导管的壳体内部， 以径向安装代替了传统轴向安装，并采用“发电系统-轮缘叶轮-导管”的一体化设计，使系统结构更加紧凑，通过轮缘叶轮与导管内侧的径向匹配，去除了轮毂结构，当系统运行时通过轮缘叶轮的旋转带动内置的发电机系统同步旋转。 因此，相比传统的导管涡轮机，无轴轮缘导管涡轮机不需要安装轴系支撑结构， 在实际运行时可大大减小流动阻力和干扰， 提升了系统的稳定性和可靠性[10]。

在实际的潮流环境中， 无轴轮缘导管涡轮机不可避免的要在波浪、剪切流、偏流等混合工况下运行， 而对其在上述工况下的水动力特性进行评估至关重要。为此，本文以斋堂岛海域的潮流条件为背景，对一无轴轮缘导管涡轮机进行了分析，探讨了其在顺流和偏流条件下的水动力特性及尾流结构形态， 以期能更好地了解无轴轮缘导管涡轮机在实际潮流条件下的运行状态， 并为其合理布置提供一定的参考依据。

1 模型与计算方法

1.1 控制方程

假定流体不可压缩， 控制方程分为连续方程及动量方程，雷诺时均的Navier-Stokes 方程可表示为

1.2 水动力学参数

涡轮机的水动力性能可用叶尖速比（TSR）、功率系数（CP）和推力系数（CT）表征，其计算式分别为

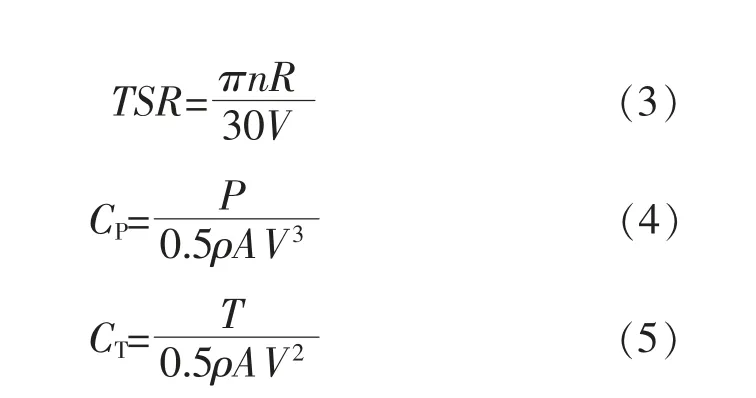
式中：n 为涡轮机转速，r/min；R 为叶轮半径，m；P为涡轮机的输出功率，W；T 为叶轮轴向推力，N；A为叶轮旋转扫掠面积，m2；V 为来流流速，m/s。

1.3 计算模型与网格划分

本文的无轴轮缘导管涡轮机由轮缘叶轮与导管组成，其中叶轮为“三叶”水平轴叶轮，其直径D为2 m，毂径比为0.1；导管为“类翼型”环形截面后置导管。在叶轮的基础上稍作调整，取消轮毂部分，并用轮缘连接叶尖，轮缘宽度比叶尖的轴向跨度略大。 将调整后的轮缘叶轮与导管内壁的喉部位置进行装配得到无轴轮缘导管涡轮机。 设置计算域中涡轮机的中心距入口距离为5D，涡轮机中心至出口距离为15D， 模型阻塞度小于1.0%，入口设置为速度入口，出口设置为压力出口，轮缘叶轮及导管为固壁面无滑移壁面条件。 将计算域划分为旋转域和静止域。 无轴轮缘导管涡轮机模型与计算域的示意图如图1 所示。

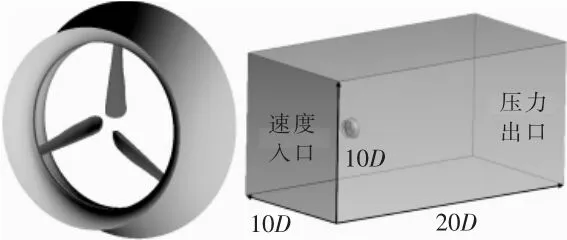
图1 模型及计算域Fig.1 Model and calculation domain

假设来流速度为1.56 m/s， 参考长度为叶轮直径（2 m），则系统的雷诺数约为3.1×106。 设置叶轮第一层边界层网格满足y+=1， 导管第一层边界层网格满足y+=10。 采用SST k-ω 湍流模型和滑移网格模型模拟非定常旋转效应， 动静交界面采用interface 设置，设置叶轮每旋转1.8°作为一个时间步长，每步的计算残差收敛最小值小于10-3,总计算时长为30 s，并取计算稳定的后6 s 作为分析结果。 此外，对无轴轮缘导管涡轮机在V=1.56 m/s 和TSR=4 的条件下进行网格数无关验证，结果如表1 所示。由表1 可知，当网格数超过600 万后，CP和CT基本不变。 对距导管涡轮机轴线距离为2D 的附近体网格进行加密， 最终网格划分总数为800 万左右，其中旋转域约为190 万，静止域约为610 万，网格细节如图2 所示。

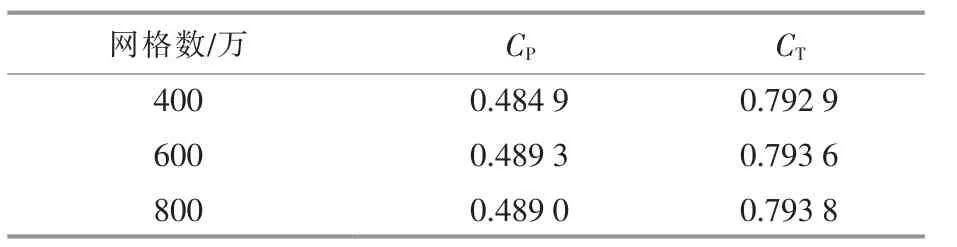
表1 网格数无关验证Table 1 Mesh independence assessment results

图2 网格细节Fig.2 Mesh details

1.4 数值验证

为了确保数值模拟的准确性， 本文对叶轮在5 种来流速度下的CFD 结果与实验值[11]进行了比较，结果如图3 所示。 从图3 可以看出，两者吻合度较好，验证了本文数值模型及方法的可靠性。

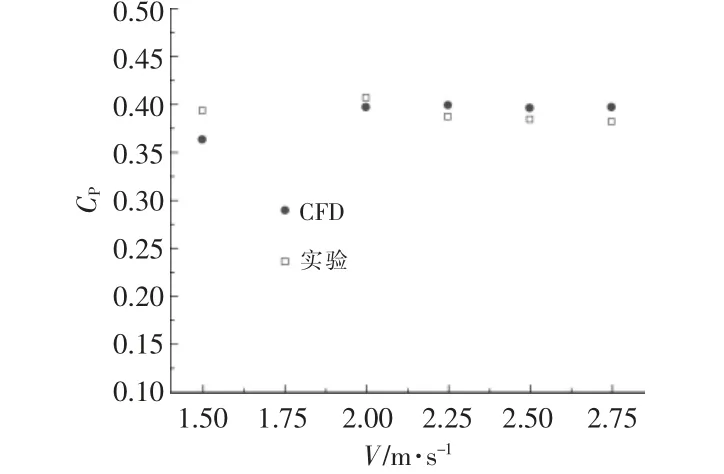
图3 实验数据与CFD 结果的对比Fig.3 Comparison between experiment and CFD

1.5 波流条件设置

以斋堂岛海域的实际潮流条件作为研究背景， 该海域的日常极限波浪参数为波高0.6 m，波长24.8 m，频率3.2 s，水深（H）与流速的关系[12]如图4 所示。由图4 可知，当水深为0～10 m（5D）时，流速约为1.56 m/s，且流速与水深的斜率，即流速剪切率为0.002。 依照该潮流条件，将速度入口条件设置为（1.56±0.002）H m/s，无轴轮缘导管涡轮机的中心距水面的距离为1D。

图4 水深与流速的关系Fig.4 The relationship between water depth and velocity

2 结果与分析

2.1 顺流条件

在不同TSR 下， 无轴轮缘导管涡轮机的CP和CT随时间的变化曲线如图5 所示。由图5 可以看出：当TSR=4 时，涡轮机处于最佳TSR 范围附近， 随着TSR 的增大， 涡轮机的平均CP逐渐降低，而平均CT逐渐升高；CP和CT的波动幅度也随TSR 产生一定的变化， 随着TSR 的增大，CP和CT的波动幅度逐渐增大；当TSR=5 时，CP和CT的波动幅度分别比TSR=4 时增加了8.4%和17.3%；当TSR=6 时，CP和CT的波动幅度分别比TSR=4 时增加了31.9%和40.9%。 由于受到波流的影响，无轴轮缘导管涡轮机在一个波流周期内的CP和CT产生了明显的周期性波动， 且波动频率与波浪频率保持一致。在波流的作用下，无轴轮缘导管涡轮机附近的流体速度分布发生了明显的变化。 当波峰位于无轴轮缘导管涡轮机正上端时， 将诱导周围水流迅速加快， 使涡轮机的CP与CT达到最大值；而当波谷位于无轴轮缘导管涡轮机正上端时，将诱导水流迅速减慢，使CP与CT处于最小值。

图5 不同TSR 下的CP 和CT 随时间的变化曲线Fig.5 CP and CT versus times curve under different TSR

当TSR 不同时，无轴轮缘导管涡轮机在波流条件下的涡量（上图）与湍动能（下图）分布如图6所示。从图6 可以看出，无轴轮缘导管涡轮机尾部存在导管后缘处的分离涡及叶轮轴心处独特的轴心射流涡。 由于导管外侧截面处出现了一定的流动分离， 导致一部分涡流能量从导管后缘边界处脱落并向下游传播。受波流的影响，该部分涡流在向下游传播的过程中呈现出不规则的形态， 其强度与范围也在不断变化。 随着TSR 的增大，尾旋涡流强度有所上升， 也导致其不规则程度有所增加。 此外， 由于无轴轮缘导管涡轮机没有轮毂结构，轴心处存在一定面积的开放缺口。当无轴轮缘导管涡轮机运行时，叶轮前后将产生压力差，该压力差将迫使一部分来流通过该开放缺口泄流而出， 并形成轴心射流涡（此处的流速高于来流量级）。 随着TSR 的增大，叶轮前后的压力差有所减小，导致通过叶轮开放缺口处的流量下降。 因此，轴心处的涡流的范围随着TSR 的增大而减小，并随着下游距离的延伸而逐渐消散至周围流场中。

图6 不同TSR 下的涡量与湍动能分布Fig.6 Vorticity and turbulent kinetic energy distribution under different TSR

2.2 偏流条件

当TSR=4 时，无轴轮缘导管涡轮机在不同偏流角下的CP和CT随时间的变化曲线如图7 所示。 从图7 可以看出：当偏流角为40°时，无轴轮缘导管涡轮机的平均CP和CT分别比偏流角为20°时降低了18.9%和10.7%；当偏流角为60°时，无轴轮缘导管涡轮机的平均CP和CT分别比偏流角为20°时降低了70.0%和45.5%； 处于偏流条件下的无轴轮缘导管涡轮机CP和CT依然表现出与波流频率一致的周期性波动。 但由于偏流增加了其运行的复杂性， 使叶轮前后端的压力差处于高度不稳定的状态， 导致CP和CT在一个波流周期内出现了额外的波动，且随着偏流角的增大，该额外波动的振幅也逐渐增大。 当无轴轮缘导管涡轮机处于偏流条件下时，首先，叶轮的叶素截面的相对攻角分布将发生改变；其次，叶轮旋转平面来流向的投影面积将会减小；最后，导管的入口流量也将减小，其聚流抽吸能力有所减弱。最终使无轴轮缘导管涡轮机的CP和CT逐渐由轴向分量转移至侧向分量，导致其平均CP和CT逐渐降低，且偏流角越大，平均CP和CT下降的越快。

图7 不同偏流角下CP 和CT 随时间的变化曲线Fig.7 CP and CT versus times curve under different yaw angles

当偏流角不同时， 无轴轮缘导管涡轮机在波流条件下的涡量（上图）与湍动能（下图）分布如图8 所示。从图8 可以看出，偏流条件下的涡流能量分布不同于顺流条件下的涡流能量分布（涡流能量分布都发生了侧向的偏移和变形）。当来流与无轴轮缘导管涡轮机结构接触时， 由于来流方向与涡轮机轴心不在一条直线上， 流体将按照流动阻力最小的路径， 绕开导管偏转的一侧外壁面并诱导形成相当程度的流动分离低速区， 该低速区直接导致了大范围的分离涡和高湍动能区， 而导管另一侧的后缘内侧也会脱落形成一定范围的分离涡并向下游传播。受波流的影响，该部分涡流能量的强度与范围会不断发生变化， 并在向下游传播的过程中呈现出极其复杂的非对称形态。 随着偏流角增大，其复杂程度也逐渐增加。 此外，一部分来流依然可以通过轴心处的开放缺口泄流而出，但随着偏流角的增大， 该开放缺口在来流向的投影面积逐渐减小，导致轴心射流涡范围所有下降。

图8 不同偏流角下的涡量与湍动能分布Fig.8 Vorticity and turbulent kinetic energy distribution under different yaw angles

2.3 讨论

由上文的分析结果可知，在一定范围内，波流相互作用下的无轴轮缘导管涡轮机将承受较大的水动力波动载荷的影响（尤其是当涡轮机转速较高或者偶遇偏流工况时）。 此外，所有这些波动载荷也将传递到涡轮机内部的元件上， 这也间接地加速了这些内部元件的磨损和疲劳程度， 给整个系统的能量输出稳定性和结构安全性都带来了一定的挑战。 鉴于潮流能发电系统的制造和维护成本都很高，且至少要保证在25 a 内无需大修或更换主要部件[13]。因此，可采用以下措施应对上述不利影响。

①尽量使涡轮机处于较低的TSR 范围内运行 （涡轮机最佳的输出功率匹配于低TSR 范围内）。此外，为了减小偏流的影响，应加装偏流旋转自适应装置， 使来流方向与无轴轮缘导管涡轮机轴向偏差在一个较小角度内。

②采用全复合材料叶片， 可在一定范围内降低水动力性能的波动幅值；或者采用合金为主体，复合材料包裹的叶片制造工艺， 可在保证叶轮刚度的同时，起到一定的抗机械疲劳，阻止表面裂纹扩展的叶片延寿作用。

③增加无轴轮缘导管涡轮机远程故障诊断与监测工序，提早锁定损伤部件，在叶片等结构发生断裂前进行修复。

3 结论

本文依据斋堂岛海域的实际潮流条件对一种新型潮流能无轴轮缘导管涡轮机在波流相互作用下的水动力特性与尾流结构进行了三维非定常数值模拟研究，得出以下结论。

①在顺流条件下，受波流效应的影响，当TSR不同时， 无轴轮缘导管涡轮机的CP和CT均产生了明显的周期性波动， 波动频率与波浪频率保持一致，且随着TSR 的增大，CP和CT的波动幅度逐渐增大。

②在偏流条件下， 无轴轮缘导管涡轮机的平均CP和CT均随着偏流角的增大而降低， 而偏流也将导致CP和CT在一个波流周期内出现额外的波动， 且该额外波动的振幅随偏流角的增大而增大。

③受波流效应的影响， 无轴轮缘导管涡轮机的尾流在向下游传播的过程中呈现出复杂的形态，其强度与范围也会不断发生变化，且随着TSR和偏流角的增大，其复杂程度也在逐渐增加。

④由于无轴轮缘导管涡轮机没有轮毂结构，轴心处存在一定面积的开放缺口。在一定条件下，一部分来流将通过该开放缺口泄流而出并形成射流涡，而随着TSR 和偏流角的增大，射流涡范围将有所减小。