直流微网的电压分层暂态稳定控制技术
2022-08-17杜方鑫张祥宇
付 媛, 杜方鑫, 张祥宇
(华北电力大学 新能源电力系统国家重点实验室, 河北 保定 071003)
0 引言
直流微电网因具有线路损耗低、适于各类电源及负载接入等特点而受到广泛关注[1],[2]。随着分布式电源及其负荷容量的不断提升,短时扰动后的恒功率负荷所表现出的负阻抗特性,对于削弱直流电压阻尼的影响愈加显著。 提高直流电压的暂态稳定性已成为直流电网稳定运行所面对的新挑战[3],[4]。
直流微电网无须考虑频率调整及无功功率补偿, 直流电压成为衡量系统稳定性的重要指标[5],[6]。 在静态稳定下,直流微电网的电压控制策略主要有主从控制和下垂控制[7]。 下垂控制结构简单, 无须通信可实现各端换流器的功率协调分配[8]。 文献[9],[10]提出了基于下垂控制的电压分层控制,该控制方法仅适于多端换流器在长时间尺度中完成功率分配,尚无法应对逐渐增加的电压振荡风险。 为分析直流电网暂态稳定性,文献[11]通过建立电压源型换流站等效阻抗模型,提出了多端直流配电网模型的小干扰线性简化方法。 随着直流系统稳定性研究的逐渐深入,恒功率负荷诱发电压振荡的问题受到了广泛关注。 文献[12]建立直流微电网的小信号模型,分析了恒功率负载的负阻尼特性对系统稳定性的影响机理。 文献[13]通过特征值轨迹分析了采用下垂控制后直流微电网的稳定性, 并利用阻抗匹配准则, 通过低通滤波增加有源阻尼抑制了电压振荡。 文献[14],[15]考虑了功率滤波、下垂特性等因素, 线性化分析了恒功率负荷和下垂系数对系统稳定性的影响。 文献[16],[17]结合恒功率负荷的特性曲线建立了小信号模型, 通过分析负荷与电源侧的电压传递函数得到系统稳定运行须要满足的条件。 上述文献虽然已针对恒功率负荷对系统暂态稳定性的影响展开了分析, 但控制策略能否适于恒功率负荷大幅增加的情况及电压分层多模式切换调压下的直流微电网,仍有待进一步探讨。
直流电网的暂态稳定性判据是评估系统安全运行须要解决的关键问题之一。文献[18]通过阻抗建模分析了多电源环形直流微电网的稳定性,并给出了稳定性判据。文献[19]结合张北直流电网架构,通过戴维南等效建立直流电网的数学模型,并得到直流电网的稳定性判据。 文献[20]通过戴维南/诺顿等效得到各功率模块的阻抗/导纳,结合系统节点导纳矩阵给出了主从控制下直流微电网系统稳定性判据, 提出了基于双准比例谐振控制器的、仅适于主从控制模式的有源阻尼控制方法。文献[21]分析了带恒功率负荷的级联系统在平衡点稳定的条件, 并提出抑制直流微电网振荡的控制策略。 然而,该策略仅考虑了恒功率负荷,忽略了阻性负荷的影响。 文献[22]分析了电压波动后直流电网运行点的移动轨迹,阐述了系统的稳定运行机理, 更适于分析系统遭遇故障后的特性恢复。 综上显示,目前亟待深入探讨适于直流电网的稳定性判据及暂态支撑控制技术。
本文将从系统的能量方程角度出发,分析受扰后的各端暂态电量变化对电压稳定性的影响,以探讨电压分层控制下直流电网的暂态稳定机理;结合系统稳定运行条件,提出基于电量变化的系统暂态稳定判据;通过附加电量拓展电压分层切换下的电压稳定裕度,提高系统暂态稳定性。 首先,结合直流微电网的伏安特性曲线, 分析系统稳定运行点的移动轨迹,推导系统的能量方程,获得基于暂态电量的稳定判据;然后,依据稳定判据得到电压分层切换下暂态电量的变化机理, 并改进源荷两侧换流器的电压分层下垂控制, 提出直流微电网的电压暂态稳定控制策略;最后,通过硬件在环系统,验证所提控制策略对系统稳定的改善作用。
1 直流微网的电压分层控制
图1 为五端直流微网的系统拓扑结构。 系统包括由换流器G-VSC 接入的交流主网、 换流器B-DC 接入的蓄电池、换流器PV-DC 接入的光伏单元、 换流器L-DC 接入的恒功率负荷和直接接入的阻性负荷。
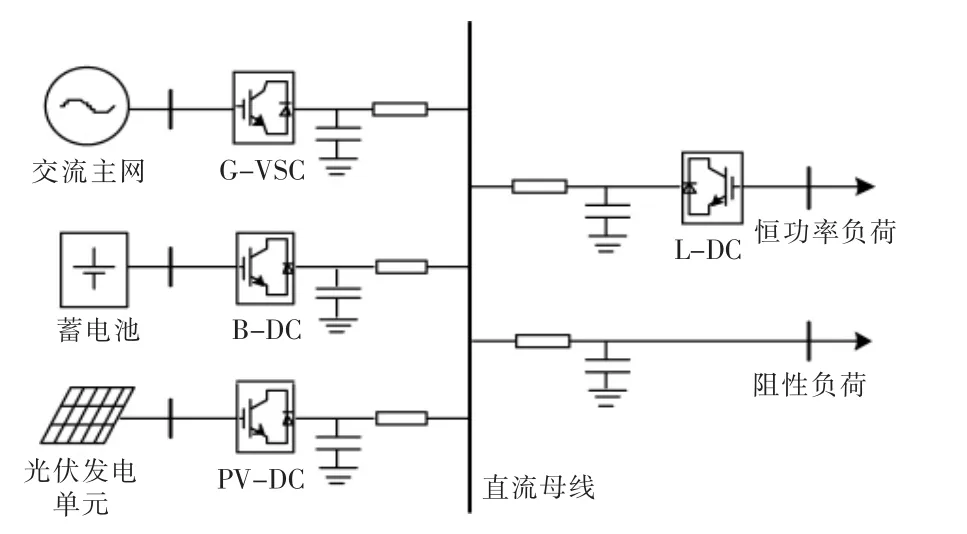
图1 直流微电网结构图Fig.1 Diagram of DC microgrid
为协调控制5 个端口, 直流微网采用电压分层控制策略,其原理如图2 所示[9]。

图2 电压分层控制策略Fig.2 Voltage hierarchical control strategy

①联网调压模式:当电压偏差|Δudc|<(0,Δu1],系统由交流主网调压,蓄电池处于备用状态,如图2 所示。G-VSC 采用u-i 下垂控制,其出口电压可表示为

②储能调压模式: 当电压偏差|Δudc|<(Δu1,Δu2]时,G-VSC 达到功率限值,失去调压能力(图2)。 蓄电池根据u-i 下垂控制电压,B-DC 出口电压为
③减负荷或弃光调压模式: 当电压偏差|Δudc|<(Δu2,Δu3]时,系统处于减负荷或弃光调压模式。 此时G-VSC 和B-DC 均达到功率限值,失去了调压能力。

当采用标幺值表示时,pPV_max=1 p.u.,则1/kPV=Δu3-Δu2。
采用电压分层控制时, 各端换流器可根据电压偏差有序参与系统功率调节, 便于实现多端协调控制。 然而,当电压大幅度变化时,系统将进入多模式调压状态。 考虑到恒功率负荷对电压的阻尼效果体现为负值, 对直流微网稳定性有不利影响,故探讨直流微网模式切换时的暂态稳定问题,以避免控制器参数设计不合理或恒功率负荷占比增加,导致系统出现振荡失稳[16],[21]。
2 基于暂态电量的直流微网稳定判据
2.1 系统稳定运行条件
在直流微网中, 交流主网和蓄电池均通过u-i 下垂控制直流电压, 可将其视为受控电压源[21],[23]。在短时振荡过程中,采用最大功率跟踪控制的光伏电源输出功率pLS近似认为不变,可将其与恒功率负荷功率pLL合并, 则功率为pL的等值负荷模型,可用受控电流源iCPL表示[13],[21]。
直流微网的等值电路如图3 所示。图中:us,is为换流器出口母线电压与输出电流;R,L 为电源、换流器和线路的等效电阻与电感;C为稳压电容;udc为直流电网电压;RL为阻性负荷。

图3 直流微网的简化等效电路Fig.3 Equivalent circuit of DC microgrid
受控电流源iCPL为

依据系统拓扑约束和元件约束, 可在udc-iCPL平面上根据式(5),(9)绘制恒功率负荷特性曲线l1和电源伏安特性曲线l2(图4)。两曲线的交点分别为A 点和B 点, 即为直流微电网的初始运行点,在此处系统电压、电流稳定,可以满足负荷的供电需求。

图4 系统udc-iCPL 特性曲线Fig.4 System udc-iCPL characteristic curves
当系统运行在A 点, 若恒功率负荷增大,负荷特性曲线l1移动至l1+, 与曲线l2相交于A+点。由于系统直流电压不能发生突变, 须要增加电流满足恒功率负荷需求,负荷运行点将先向右移动,再沿曲线l1+向A+点移动。 电源的下垂控制则在电流增大后减小直流电压,运行点沿曲线l2向A+点移动,最终交汇于这一新的稳定运行点。同理可分析,负荷功率减少后,最终交汇于A-点新的稳定运行点。 综上所述,当系统运行于A 点,直流微电网具备暂态稳定恢复能力。
当系统运行在B 点, 若恒功率负荷增大,负荷特性曲线l1移动至l1+, 与曲线l2相交于B+点。在电压不变情况下, 为满足功率需求须增加负荷电流,负荷运行点向右上方移动。电源下垂控制则在电流增大后减小直流电压, 电源运行点沿曲线l2向B-点移动,系统运行点不会交汇于预期的B+点,否则系统将无法稳定运行。 同理可分析,负荷减小后, 系统运行点也不会交汇于预期的B-点,否则系统将失去稳定性。由此可知,当系统运行于B 点时,直流微电网不具备暂态稳定恢复能力。
综上分析显示, 系统具备暂态稳定恢复能力的运行点应为A 点。 系统稳定运行点应满足的必要条件为

2.2 直流微网的稳定判据
为便于分析直流微电网运行参数对系统稳定判据的影响,联立式(6)~(8),并在平衡点附近线性化得到系统小扰动模型为


当系统稳态运行,udc为常数,且系统参数C,R,k,L,RL恒定, 则iSeq,iL与udc成线性关系,iSeq+iL=udc[C(R+k)/L+1/RL]。 图5 为该判据的示意图,QS+QL为电源侧和阻性负荷侧电量之和;QCPL为恒功率负荷侧电量。 当电源侧和阻性负荷侧电量之和大于恒功率负荷电量时, 系统具备暂态稳定运行能力。
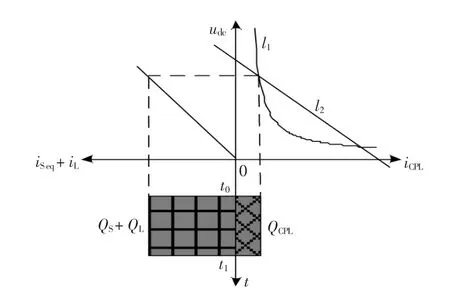
图5 电量判据示意图Fig.5 Diagram of electric quantity criterion
3 直流微网分层模式切换下的电量分析与控制技术
3.1 切换至储能调压模式时的电量分析与控制技术
系统在联网调压模式下运行于A0点,交流主网调压的下垂控制系数为kg。 当恒功率负荷增加或光伏功率减小,等效恒功率负荷增加ΔpL,超过G-VSC 功率限值。 系统切换为储能调压模式,下垂控制系数变为kb,母线电压下降Δudc,下垂系数的变化量Δk=kb-kg。
切换调压模式时,系统暂态电量变化如图6所示。

图6 切换至储能调压模式的电量变化示意图Fig.6 Diagram of electric quantity variation when switching to energy storage voltage regulation mode
恒功率负荷增加由l1移动至l′1,电压不变电流将增加, 负荷运行点移动轨迹为A0→A′0→A1。电源在下垂控制下,电流增大,电压降低,电源运行点移动轨迹为A0→M, 在M 点G-VSC 达到功率限值,切换为蓄电池调压,电源运行点将沿M→A1移动。 最终电源与负荷都达到新的稳定运行点A1,系统稳定运行。
调压模式切换, 下垂系数发生变化, 根据式(14)有:

恒功率负荷增加, 负荷曲线变化使得QCPL增加了ΔQCPL。在调压模式切换的过程中,电压下降,下垂系数变化了Δk, 最终使得QS+QL增加了ΔQS+ΔQL,并且该电量的变化趋势与Δudc和Δk 有关。根据式(17),若QCPL增加了ΔQCPL,不利于系统稳定,显然会有失稳风险。

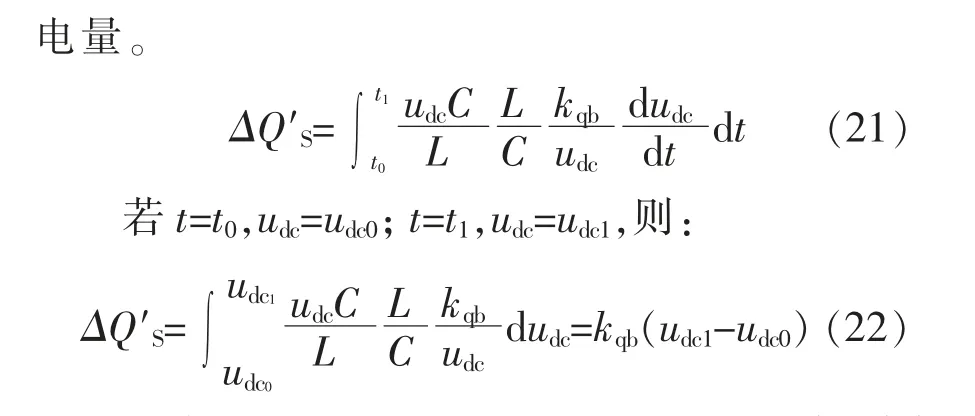
由式(22)可以看出,在电量累积过程中,附加电量控制系数kqb可等效为储能侧附加了电容。
若udc1>udc0,则取kqb>0;若udc1<udc0,则取kqb<0,即可保证ΔQ′S>0。改进后的储能侧控制策略如图7 所示。在传统u-i 下垂控制的基础上,将电压变化率按照公式(19)引入下垂系数中,通过改变下垂系数增加储能侧在暂态过程中的累积电量,提高系统运行稳定性。

图7 储能侧控制策略框图Fig.7 Diagram of energy storage side control strategy
3.2 切换至减负荷调压模式时的电量分析与控制技术
当直流电压跌落导致系统进入减负荷调压模式后,负荷、光伏侧换流器仍采用功率和电流双环控制。 此模式下,负荷、光伏模型仍可采用受控电流源表示,但其输出电流会因功率调整而改变。系统在储能调压模式下运行于A1点,当光伏功率减小时,等效恒功率负荷增加,此时B-DC 达到功率限值(N 点,图8)。

若光伏功率持续减小,电压进一步下降,系统切换为减负荷调压模式,L-DC 根据u-p 下垂曲线调整功率需求。将式(5)代入式(3),得到负荷特性udc-iCPL的关系为切换调压模式时的系统暂态电量变化如图8所示。
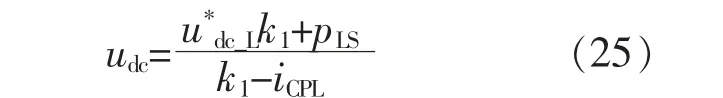

图8 切换至减负荷调压模式的电量变化示意图Fig.8 Diagram of electric quantity variation when switching to load reduction voltage regulation mode
如图8 所示,光伏功率减小,等效恒功率负荷增加,电压不变,电流将增加。切换调压模式后,负荷曲线为l, 负荷运行点移动轨迹为N→N′→A2。电源在式(24)控制下,电流增大电压降低,运行点移动轨迹为N→A2。 最终电源与负荷都达到新的运行点A2,系统稳定运行。 光伏功率减小,等效恒功率负荷增加, 负荷曲线变化使得QCPL增加了ΔQCPL,在调压模式切换的过程中电压下降,系统的电量QS+QL减小了ΔQS+ΔQL。 根据式(17),QS+QL减小后,不利于系统的稳定,仍有失稳风险。
为减少恒功率负荷的暂态电量QCPL, 可在下垂控制中引入直流母线电压udc、电压偏差Δudc和电压变化率dudc/dt,则下垂系数可表示为


由式(29)可以看出,可将kql等效为负荷侧的附加电容。
若udc1>udc0,则取kql<0;若udc1<udc0,则取kql>0,即可保证ΔQ′CPL<0。 恒功率负荷侧换流器的控制结构如图9 所示。在传统u-p 下垂控制的基础上,将电压变化率、 电压偏差和直流电压按照公式(26)引入下垂系数中;通过改变下垂系数减少恒功率负荷侧电量,提高系统运行稳定性。

图9 恒功率负荷侧控制策略框图Fig.9 Diagram of constant power load side control strategy
当直流微网进入减负荷调压模式时,根据up 下垂曲线输出功率, 下垂系数为kl。 在此基础上, 在下垂系数中引入电压变化率和电压偏差信号,则改进后下垂系数为k′1,可通过切换u-p 下垂曲线,减少负荷侧电量。
直流微网在分层控制下还包括联网运行和弃光调压模式。 考虑到并网变流器稳压时,直流电压波动较小,可由交流主网平抑,故本文重点关注进入储能调压后的电压稳定问题。此外,若光伏输出功率大量增加,系统将进入弃光调压模式。在此模式下,光伏功率增加后,可认为等值恒功率负荷减小。 显然,当恒功率负荷较小时,系统稳定性会随之增强[13],[21]。 考虑到系统稳定裕度较为充足,光伏减功率直至电压恢复至储能调压层即可,一般不存在振荡风险,故不再讨论弃光调压模式切换时的电压暂态稳定问题。
4 硬件在环仿真验证
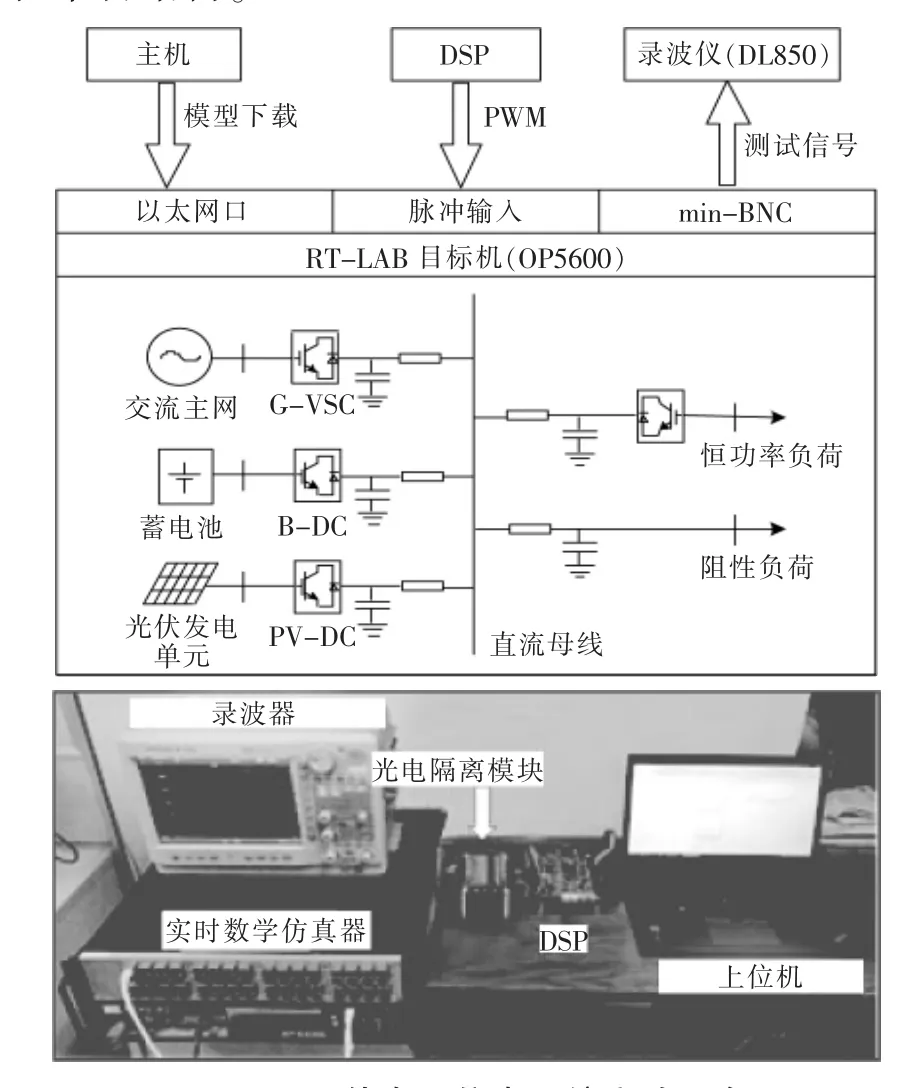
图10 硬件在环仿真系统实验平台Fig.10 Hardware-in-the-loop simulation system experimental platform
实验平台包含RT-LAB 实时数字仿真器(OP5600)、DSP 主板 (TMS320F28335)、 录波仪(DL850)以及上位机。 其中:直流电网各端换流器的控制算法部署在DSP 中; 直流电网的实时仿真模型部署在RT-LAB 中;RT-LAB 通过以太网口与主机相连;DSP 产生PWM 脉冲送至RTLAB 的脉冲输入端口;RT-LAB 的min-BNC 接口与DL850 录波仪相连, 用以显示测试波形。在实验平台中, 直流微网各端口的参数如表1所示。

表1 测试平台参数Table 1 Test platform parameters
4.1 储能调压模式下的电压跌落
在初始状态下, 系统带恒功率负荷和阻性负荷分别为15 kW 和4.82 kW; 光伏输出功率保持不变为5 kW; 蓄电池处于备用状态无输出;GVSC 在电压下垂控制下输出功率为15 kW; 直流电压稳定在491 V。
在0.4 s 时刻, 恒功率负荷突增至35 kW,GVSC 达到功率限值,系统内出现功率缺额,电压下降,切换为储能调压模式。 图11 为在传统电压分层控制与所提改进控制策略下,直流电压、蓄电池换流器、交流主网换流器、光伏单元换流器、恒功率负荷以及阻性负荷功率输出的动态响应对比。

图11 储能调压模式的系统动态响应Fig.11 Dynamic response of energy storage voltage regulation mode
由于恒功率负荷增加, 引入了更强的负阻尼效应。 根据直流微网电压分层控制需要设计出的下垂系数, 在模式切换时无法解决系统存在持续性振荡风险的问题。 将系统参数代入式(14),则QS与QL分别为0.6 C 与0.68 C。 当负荷变为35 kW 后,QCPL变为4.31 C, 则QS与QL之和为1.28 C<QCPL,显然不满足系统暂态稳定判据,系统无法稳定运行。如图11 可见,当负荷突增,直流微网在传统的电压分层控制策略下进入储能调压模式,但不满足暂态稳定判据,直流电压、蓄电池功率及阻性负荷功率均发生了持续性振荡, 电压振幅约为17 V。
在改进控制策略中, 储能侧附加电量控制系数设置为kqb=2,则由式(22)可计算出,储能改进下垂控制后提供的附加电量ΔQ′S为4 C。 在此条件下, 系统电量之和为QS+ΔQ′S+QL=5.28 C>QCPL。由式(17)可知,此时满足了直流微网的暂态稳定判据要求。如图11 所示,负荷增加相同容量,直流电压的振幅减少为2 V, 系统可以更加平稳地切换到储能调压模式中,直流电压稳定在487 V;蓄电池输出功率稳定在15 kW, 阻性负荷功率随直流电压降低而降低,稳定在4.72 kW。
4.2 减负荷或弃光调压模式下的电压跌落
在初始状态下, 系统带恒功率负荷和阻性负荷分别为19.5 kW 和4.8 kW;光伏输出功率5 kW; 蓄电池处于备用状态无输出;G-VSC 按照电压下垂控制输出功率19.3 kW; 电压稳定在490 V。
在0.4 s 时刻断开与主网连接,G-VSC 输出功率降为零,系统内出现功率缺额,电压下降,进入储能调压模式;蓄电池发出功率,直流电压稳定在485 V。0.5 s 时刻光伏输出功率突减为零,电压再次下降,进入减负荷调压。在传统电压分层控制与改进控制策略下,直流电压、蓄电池换流器、交流主网换流器、光伏单元换流器、恒功率负荷以及阻性负荷功率输出的动态响应对比如图12 所示。
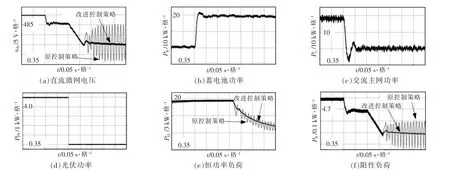
图12 减负荷模式的振荡与抑制Fig.12 Dynamic response of load voltage control mode
将系统参数代入式(14),则QS与QL分别为0.67 C 与0.76 C。 光伏功率突减后,QCPL变为3.28 C,则QS与QL之和为1.43 C<QCPL,显然不满足系统暂态稳定判据,系统无法稳定运行。 如图12 所示,当光伏功率突减,直流微网在传统的电压分层控制策略下进入减负荷调压模式, 不满足暂态稳定判据;直流电压、蓄电池功率及阻性负荷功率均发生了持续性振荡,电压振幅约为19 V。
在改进控制策略中, 恒功率负荷侧附加电量控制系数设置为kqb=-2。 由式(29)可计算出恒功率负荷改进下垂控制后提供的附加电量ΔQ′CPL为-2 C。 在此条件下, 系统电量之和为QS+QL>QCPL+ΔQ′CPL=1.28 C。由式(17)可见,此时满足了直流微网的暂态稳定判据要求。 如图12 所示,光伏发电减少输出相同功率,直流电压的振幅减少为1 V,系统可以更加平稳地切换到减负荷调压模式中;直流电压稳定在475 V, 蓄电池功率稳定在20 kW;阻性负荷功率随直流电压降低而降低,稳定在4.5 kW。
4.3 电压抬升后的调压模式切换
在初始状态下,系统带恒功率负荷和阻性负荷分别为15 kW 和5 kW, 电源侧光伏输出功率20 kW,蓄电池处于备用状态无输出, 光伏功率恰好等于负荷功率,G-VSC 输出功率0 kW,电压稳定在499 V。
在0.3 s 时刻断开G-VSC,进入孤岛运行。在0.5 s 时刻光伏功率突增至30 kW,系统内功率过剩,电压上升,进入储能调压模式,蓄电池吸收功率为10 kW, 电压稳定在510 V 左右。0.7 s 时刻负荷突减至0 kW,电压再次上升,蓄电池吸收功率达到限值20 kW, 进入弃光调压模式,不得已减少光伏输出功率为27 kW,电压稳定在525 V。 直流电压、蓄电池换流器、交流主网换流器、光伏单元换流器、恒功率负荷以及阻性负荷功率输出的动态响应对比如图13所示。
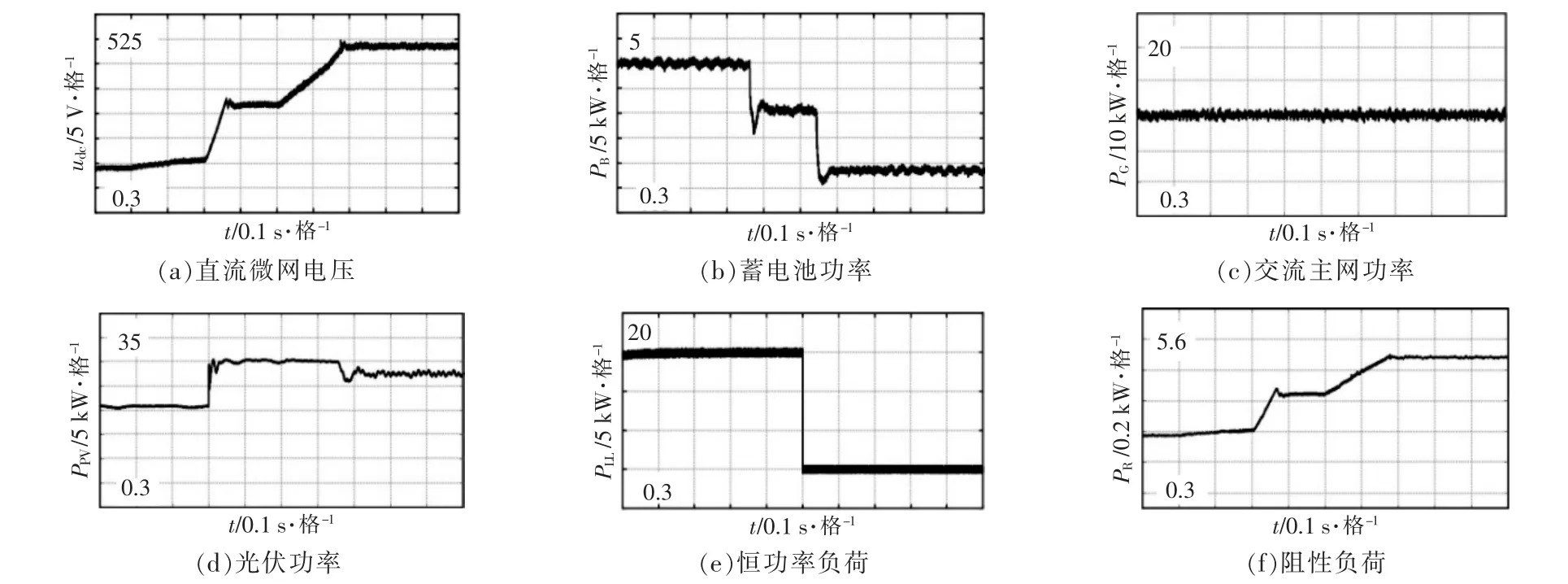
图13 弃光调压模式的仿真Fig.13 The simulation of light abandoning voltage control mode
5 结论
为提高采用电压分层控制后直流微网的暂态稳定性,本文通过电量计算,分析了系统的暂态稳定判据, 并提出多端换流器的电压分层暂态稳定控制方法。通过理论分析和仿真验证,得到如下结论。
①直流微网可通过电量计算为系统暂态稳定提供判断依据。通过建立直流微网状态方程,系统保持渐进稳定性, 须满足电源侧和阻性负荷侧累积电量之和大于恒功率负荷侧累积电量的运行条件;若不满足该条件,系统将会面临失去运行点而失稳的风险。
②直流微网采用电压分层控制时, 若遭受扰动将进入多模式切换状态。然而,根据所提系统的暂态稳定判据,恒功率负荷累积电量增加后,在恒定的下垂控制下, 电源侧和阻性负荷侧累积电量将受分层运行范围限制。若提供电量不足,则会存在失稳风险。
③根据直流微网的电量分析,可将直流电压变化率引入分层下垂控制之中,结合有序的控制模式,使储能、负荷提供附加电量,为直流微网提供暂态支撑。 在本文所提出的控制策略下,直流微网不仅能够实现分层模式的平稳切换,还可通过在储能调压模式下增加电量或在减负荷调压模式下减小电量的方式,显著提高系统的暂态稳定性。
在电压短时振荡过程中, 光伏出力近似认为恒定, 将其与恒功率负荷等值处理的简化方法仍存在误差。另外,所提基于暂态电量的直流微网稳定判据采用了小扰动线性化分析方法。 今后须继续重点关注新能源功率波动, 建立适于在大扰动或故障情况下的暂态能量函数, 从而进一步完善直流电网的暂态稳定判据。
