点吸式波浪能直线发电机定位力优化分析
2022-08-17李永国郑丁健朱秋莹
李永国, 覃 灿, 杜 杰, 郑丁健, 朱秋莹
(1.上海海洋大学 工程学院, 上海 201306; 2.上海海洋可再生能源工程技术研究中心, 上海 201306)
0 引言
波浪能是一种可再生、周期性强、储量大的清洁能源,在我国分布广泛,主要集中在南海海域和台湾以东海域, 其能量密度在秋冬季节有着较大增幅[1]。 波浪能发电技术无疑将是达成“碳中和”这一最终目标的重要技术手段。
目前,在波浪能发电装置的研制中[2],[3],点吸式波浪能发电装置作为一种综合性能较优的波能转化装置,其核心部件永磁直线发电机具有能量转化效率高、结构简单等优点。 由于发电机的初级定子相对于次级永磁体长度较短,在定子端部会产生较为明显的磁感应波动,进而产生定位力。定位力的存在将导致噪音、振动,同时也影响反电动势的波形[4],为得到较高的发电效率,不同质量的直线发电机对定位力大小的需求也不同[5]。 针对定位力优化的研究,Prudell J[6]对圆筒型直线发电机的初级结构进行优化设计,将定子的端部齿设计为45 °倒角, 以此减小定位力。Goto A[7]提出了一种新型的动子结构,在两个磁极之间用一块中心磁轭间隔开,构建两个磁极部分与中心磁轭连接的模块化动子结构。Liu C Y[8]提出一种准Halbach 的永磁体磁化结构,并构建辅助槽和凸定子结构,采用傅里叶分析法对不同极槽比的定子结构进行分析比较,验证了该方法可有效削减定位力。 Hu H Z[9]对定位力进行频谱分析,基于基波的相位差,通过迭代计算获得定子铁心的最佳长度。
上述研究通过改变发电机各部件的结构样式和尺寸,或改变磁极的相位,使定子端部分布不均匀的磁感应强度趋于合理。 但其简单地将削减定位力与直线发电机的优化等同起来, 忽略了定位力的变化对直线发电机发电效率的影响。 且大多仅研究了单一变量对定位力的影响,并未考虑多因素共同作用时定位力的变化情况,优化效果不佳。
本文着眼于新能源的开发和利用, 基于直线发电机模型[10],利用有限元仿真和正交试验[11],[12]方法,研究直线发电机在边齿齿高、齿宽和气隙多因素共同作用下,发电性能和定位力的变化情况。分别以发电效率最高和定位力最小为优化目的,设计两个优化方案, 对比不同优化模型的性能参数, 探究在直线发电机的优化过程中定位力的优化方法。
1 直线发电机理论模型
直线发电机模型是基于点吸式波浪能的直线发电装置。由图1 可知,该装置的浮标在波浪能的激励下, 牵引永磁直线发电机的动子进行往复的直线运动,从而使动子与定子发生相对运动,进而改变了定子中线圈绕组的磁通量,产生电流,完成波浪能到电能的转变。
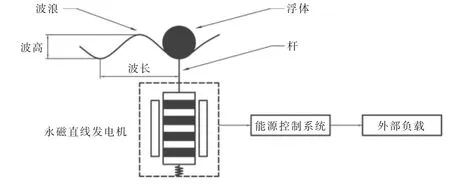
图1 点吸式波浪能发电装置示意图Fig.1 Diagram of point absorption wave energy generator
1.1 动子运动方程
圆筒型直线发电机在工作过程中主要受到3种力的作用,分别是弹簧的弹性力、定子与永磁体之间的电磁阻力、 流体作用于并联机构中动平台的激励力,即波浪力[13]。 根据牛顿第二定律,可以得到:

式中:Fh为圆筒受到的水平方向力,N;Ff为圆筒所受到的浮力,N;CD为垂直于圆筒轴线上的拖拽力系数;D 为圆筒直径,m;CM为波浪对圆筒的附加质量系数;l 为圆筒的吃水深度,m;ρ 为流体密度,kg/m3;vx为流体速度垂直于浮体轴线的分量,m/s;g 为重力加速度,kg/N。
结合式(1),(2),可建立圆筒型直线发电机的运动数学模型,将其视作由弹簧、质量、阻尼器所组成的运动系统, 在波浪力的作用下做二阶有阻尼受激振动。 当该波浪能发电装置与外部激励发生共振时,装置对波浪能的吸收率达到最大。参照文献[10]中的仿真参数,浮子为圆台形,顶面半径为0.3 m,底部半径为0.225 m,浮子高为0.45 m,吃水深度为0.25 m。 在波高为0.2 m、周期为2 s、水深为5 m 的海况条件下, 直线发电机的动子运动速度选定为0.3 m/s。
1.2 直线发电机发电效率计算

1.3 直线发电机定位力分析
由于直线发电机定子相对于动子永磁体为有限长度,故会存在端部效应,即在定子端部磁感应强度分布较为紊乱,定子受到永磁体的磁性作用,产生定位力(图2)。 定位力由端部力、齿槽力和径向力组成。

图2 直线发电机定位力示意图Fig.2 Diagram of detent force of linear generator
根据王昊[14]对直线发电机定位力的分析,运用集中法思想, 将直线发电机磁路中各部分介质理想化为不同阻值的电阻,如图3 所示。引入磁路分布系数ki,表示磁极i 与磁极i-1 形成的磁回路中,第i 个磁极宽度占整个磁极宽度的比例,ki取值为0~1。
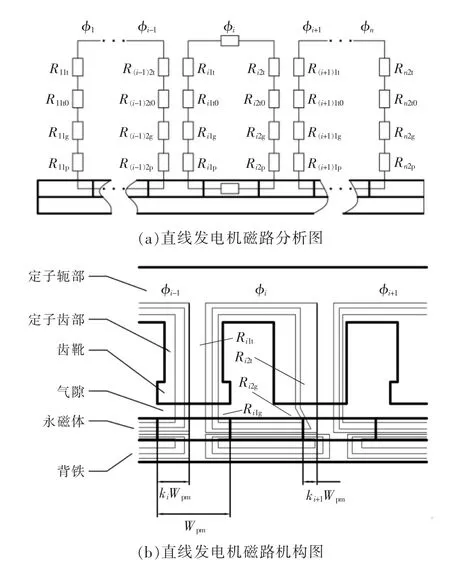
图3 直线发电机磁路分析原理图Fig.3 Schematic diagram of magnetic circuit analysis of linear generator

根据能量密度um=B2/(2μ), 可求得整个定子的能量为

两个处于端部的磁极只能和相邻的一个磁极形成磁路,即k1=0,kn=1,磁路分布系数不相等,出现了磁感应强度分布不均衡, 此时磁场中的能量E 随位置的波动很大,意味着定位力也很大。当改变定子的结构尺寸时, 特别是改变边齿的结构尺寸, 相当于改变了第1 和第n 条磁路中的电阻阻值,即改变了磁场中的能量波动,使定位力大小发生变化[14]。故后续研究将以直线发电机边齿齿高、齿宽和气隙为研究对象, 探寻不同的结构尺寸参数时发电机的运行情况。
2 有限元仿真和正交试验
2.1 直线发电机仿真模型建立
本文基于文献[10]中的直线发电机模型进行研究(图4),该模型定子采用非对称槽结构,由中心齿、T 型齿和边缘齿组成,可有效减少动子所受到的定位力,增大气隙中的磁感应密度。4 个线圈呈饼状缠绕,连接构成单相绕组。动子由背铁和环形永磁体组成, 环形永磁体分别为径向充磁和轴向充磁,相互交错排列构成Halbach 阵列,使单侧具有较强的磁感应强度。 模型详细参数见表1。

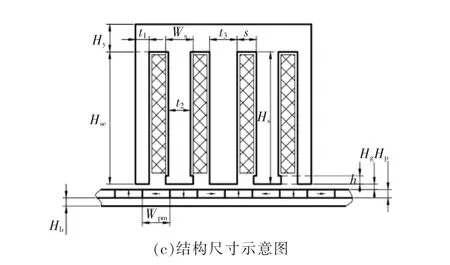
图4 直线发电机初始模型示意图Fig.4 Diagram of the initial model of the linear generator

表1 直线发电机初始模型结构参数Table 1 Structural parameters of the initial model of linear generator
2.2 直线发电机有限元仿真
Ansys Maxwell 是一款强大的电磁场仿真软件,根据表1 参数,建立数值仿真模型。 由于直线发电机发电功率尚处于优化阶段, 故外部电路设计可不采用最佳负载, 初步统一为10 Ω 外部负载,各物性参数设定为默认值。
根据上文讨论结果,选取边齿齿高、边齿齿宽和气隙作为优化对象。 同时为保证线圈绕组能嵌入齿槽内,槽宽尺寸不变,忽略因边齿齿宽变化而引起的定子轴向长度变化。根据标准水平正交表,拟定两因素六水平和一因素三水平的混合正交试验。为使仿真结果更具说服力,在考虑优化对象实际情况的同时, 尽可能以初始模型尺寸为中心点进行取值,边齿齿高Hse=33~48 mm,初始值为48 mm;边齿齿宽t1=3~8 mm,初始值为5 mm;气隙Hg=1~2 mm,初始值为2 mm。 将直线发电机反电动势、电路电流、动子所受定位力以及气隙磁感应强度作为仿真结果进行输出。 为观察各性能参数的变化趋势,将仿真结果绘制成三维图,如图5 所示。

图5 各性能参数随边齿齿高、齿宽和气隙变化情况Fig.5 Performance parameters vary with height and width of the edge tooth and air gap
由图5 可知:
①性能参数中,Hg=1 mm 的曲面均高于Hg=1.5,2 mm 的曲面; 各性能参数均随着Hse的增加而增大,且在Hse=40~48 mm 时急剧增大,气隙的磁感应强度随着Hse的增加而增强。 这是由于空气的磁导率较低,当Hg变小或Hse增加时,原空气部分被磁导率更高的铁心所取代,磁损耗减少,提高了发电性能, 同时也改变了定位力的波动程度;
②定位力随着t1的增加先减小后增大,功率随着t1的增加先增大后减小。 这是由于t1的变化会使两端的磁路分布系数发生改变,当t1达到某个值时,端部磁路分布均衡,定位力的波动程度降低。 磁路分布均衡的同时也增加了线圈中的磁通量,增大了发电机的输出功率。
2.3 正交试验与极差分析
在数值仿真过程中已预先确定了优化对象的因素和水平,如表2 所示。为探究定位力的优化方向,设计两种优化方案,方案1 以功率最大化作为优化目标,方案2 以定位力最小化作为优化目标,每种方案确定一组最优参数组合,进行比较分析。根据表中的因素和水平, 由SPSSUA 生成混合水平正交表L36(6231),并填入相应的仿真结果,具体见表3。

表2 优化对象的因素和水平Table 2 Factors and levels of optimization objects

表3 混合水平正交表和试验结果Table 3 Mixed-level orthogonal array and test results
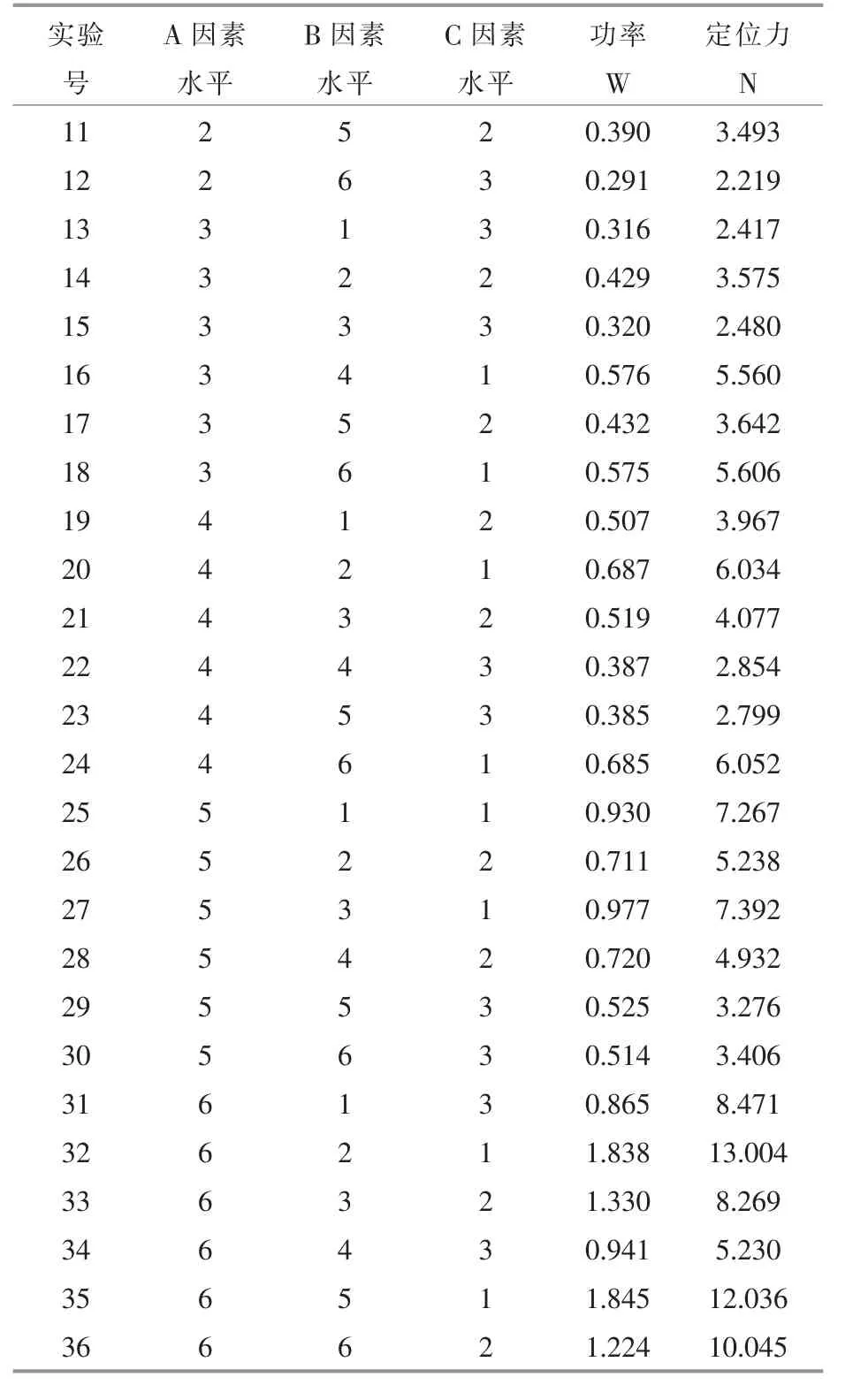
续表3
对表3 中试验结果进行极差分析, 结果见表4、表5。 为便于表达,表中:A 表示Hse因素;B 表示t1因素;C 表示Hg因素; ⅠA,B~ⅥA,B表示因素A,B 在水平1~6 下功率或定位力的均值;ⅠC~ⅢC表示因素C 在水平1~3 下功率或定位力的均值;R1A,R1B,R1C表示因素A,B,C 在功率上的极差值;R2A,R2B,R2C表示因素A,B,C 在定位力上的极差值。极差越大,表征该因素对这一性能的影响程度越大,反之越小。
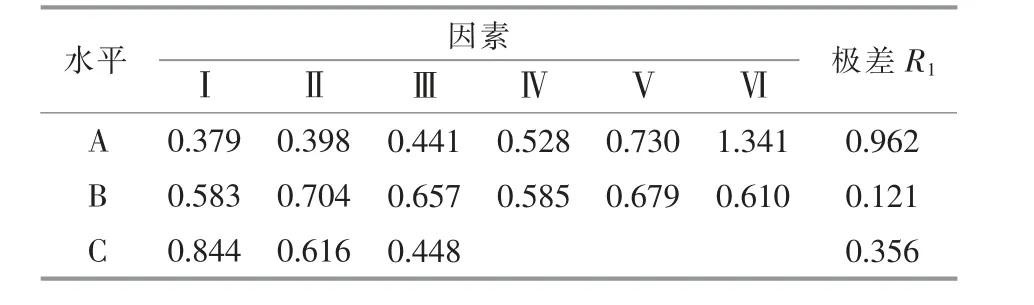
表4 正交试验功率极差分析Table 4 Power range analysis table of orthogonal test

表5 正交试验定位力极差分析Table 5 Detent force range analysis table of orthogonal test
通过极差分析,R1A>R1C>R1B且R2A>R2C>R2B,故Hse对直线发电机功率和定位力影响最大,Hg次之。 将正交试验的结果与数值仿真的结果进行比较,各性能参数的变化趋势基本吻合,表明数值仿真的结果可靠。 在功率极差分析和定位力极差分析中,ⅠA<ⅡA<ⅢA<ⅣA<ⅤA<ⅥA,故Hse的选择水平越高,功率就越大,定位力也越大;且ⅠC>ⅡC>ⅢC,故Hg的选择水平越高,功率就越小,定位力也越小。 由此可见,功率与定位力大致呈正相关,但非线性的。
3 研究结果讨论及分析
根据正交试验和数值仿真结果, 方案1 选用Hse=48 mm,Hg=1 mm 的功率最大参数组合,方案2选用Hse=33 mm,Hg=2 mm 的定位力最小参数组合。 由于边齿齿宽t1对功率和定位力的影响程度相对较小,故在正交试验中无法确定最优数值。通过图5(b),(c)可知,在Hse和Hg因素影响下,功率与定位力大致呈非线性正相关, 但在t1影响下,功率与定位力有着相反的变化趋势。故可通过数值仿真结果, 绘制单一因素作用时的性能参数曲线,以此判断最优t1,见图6。
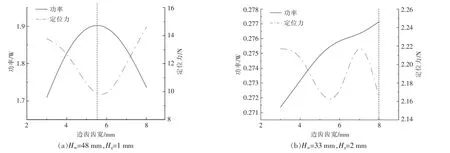
图6 功率、定位力随边齿齿宽变化情况Fig.6 The power and detent force change with the tooth width of the edge tooth
由图6(a)可知,在Hse=48 mm,Hg=1 mm,t1不断增大的情况下,发电机输出功率先增大后减小,定位力先减小后增大。 由图6(b)可知,在Hse=33 mm,Hg=2 mm,t1不断增大的情况下, 发电机输出功率不断增大,但在t1=6~7 mm 时,功率的增长有一定放缓,定位力先减小后增大,最后再减小。 这是由于磁路分布的改变, 造成线圈中磁通量的变化, 从而使定位力的波动程度以及发电机输出功率均发生了改变。 为了能在获得最大输出功率的同时,受到最小定位力的影响,在考虑制造工艺的基础上, 方案1 中t1取5.5 mm, 方案2 中t1取8 mm。 确定优化参数组合后,将优化后的性能参数绘制曲线图,如图7 所示。
由图7 可知:两种优化方案所得到的模型,各性能参数的周期性没有发生变化, 方案1 优化模型的功率均值增大102.9%,电压均值、电流均值增大42.3%,气隙磁感应强度均值增大11.1%,定位力均值增加46.3%; 方案2 优化模型的定位力均值减小66.5%,功率均值减小70.6%,气隙磁感应强度均值减弱1.8%,电压均值、电流均值减小45.4%。


图7 优化前后各性能参数对比曲线Fig.7 Comparison of performance parameters after optimization
由图7(b)可知,方案1 优化模型的定位力存在负方向作用时间延长的现象, 方案2 优化模型的定位力波动较小。 这是由于方案2 优化模型的定子端部磁路分布均衡,削弱了端部效应的影响,而方案1 优化模型的边齿齿宽增加, 使定子齿与永磁体的作用区域更大,增加了作用时间,同时也改变了端部的磁路分布, 增大了定位力的波动程度。
由图7(d)可知,由于气隙的减小,方案1 优化模型的气隙磁感应强度有着较大的增幅。
4 结论
本文利用有限元仿真和正交试验的方法,分别以发电效率最高和定位力最小为优化目的,设计两个优化方案。研究直线发电机在边齿齿高、齿宽和气隙多因素共同作用下, 发电性能和定位力的变化情况,探究在直线发电机的优化过程中,定位力的优化方向。 通过对比不同优化模型的性能参数,得出以下结论。
①对直线发电机定位力和输出功率影响最大的优化对象是边齿齿高,其次是气隙,影响最小的是边齿齿宽。
②本文仅选取了功率最大化与定位力最小化两种极端状况下的最优参数组合,在齿高、齿宽和气隙三因素作用下,功率与定位力大致呈正相关,但非线性的。
③将功率最大化作为优化目的时, 发电机功率均值增大102.9%, 定位力均值增加46.3%;将定位力最小化作为优化目的时, 发电机定位力均值减小66.5%,功率均值减小70.6%。 在直线发电机的整体优化中, 不能只考虑定位力对直线发电机的负面影响, 还需结合定位力对输出功率的影响。 在直线发电机功率优化后, 再适当削减定位力,实现直线发电机高效、平稳的运行。
