深潜耐压壳钛合金材料低周疲劳预测方法
2022-08-17莫秀珍刘刚黄一
莫秀珍, 刘刚,2, 黄一,2
(1.大连理工大学 运载工程与力学学部,辽宁 大连 116024; 2.大连理工大学 工业装备结构分析国家重点实验室,辽宁 大连 116024)
深潜器耐压壳体是由多个瓜瓣半球焊接或冲压赤道焊接等工艺制成的大开口厚球壳。人孔、观察窗等开口导致结构的不连续,加上焊接引起的各种缺陷以及焊接残余应力造成的局部塑性变形,这些区域易于形成应力集中导致疲劳裂纹的萌生和扩展进而发生破坏[1-2]。目前常用的低周疲劳分析方法主要包括基于经验与数理统计相结合的ε-N曲线法[3]以及基于断裂力学理论的裂纹扩展分析方法[4-5]。ε-N曲线法应用简单,但预测精度差,只能较为粗略地估计裂纹从成核至断裂的总体寿命,且无法确定结构的剩余寿命。断裂力学方法则以宏观可见裂纹为前提,主要预测疲劳裂纹扩展寿命,但无法预测疲劳裂纹萌生阶段的寿命。
近年来,连续损伤力学的发展为疲劳分析提供了一种概念和方法,它主要研究材料内部缺陷的产生和发展所引起的宏观力学效应及最终导致材料破坏的过程和规律[6]。与传统疲劳分析方法相比,基于损伤力学的疲劳分析方法能够将裂纹萌生和扩展统一在同一理论框架下进行分析和描述,可以更好地预测疲劳寿命。
然而,在经典的低周疲劳损伤评估模型中,为了简化计算,一般是基于拉伸和压缩引起的损伤相同的假设进行分析计算[7],即忽略压缩时微裂纹闭合效应的影响。已有研究表明,材料在受拉与受压状态下的损伤不同[8]。在受到拉伸载荷作用时,承载面上的缺陷区域(如微裂纹、微空洞等)无法承载,但在受压时,材料中一些微裂纹存在闭合行为[9],使原来的某些缺陷位置能够承载。对于深潜器耐压壳体结构,其在服役过程中受到静水压力作用,结构中大部分区域处于常温、受压状态,如果仍采用工程上常用的基于拉压引起的损伤相同的演化模型计算耐压壳体的疲劳损伤将会导致明显的误差。在当前考虑拉伸与压缩引起损伤差异的演化分析方法中,一种常用的简化处理方法是引入阶跃函数[7],当主应力状态为负时不计算损伤,忽略压应力对损伤的影响;还有一些学者把研究对象按各向异性材料处理[10]。对于前者,直接忽略压应力的损伤,显然对于深潜器耐压壳体的低周疲劳问题不适用,因为耐压壳体在作业时以受压为主,如果忽略压应力下的损伤,那么预测的结果会偏于危险;对于后者,各向异性问题大大地增加了求解难度,不方便用于工程实际。
本文针对耐压壳体的钛合金材料,在经典的Lemaitre模型基础上,建立了考虑裂纹闭合效应的低周疲劳损伤评估方法。首先,基于裂纹闭合效应和Lemaitre疲劳损伤累积模型,推导出新的考虑裂纹闭合效应的低周疲劳损伤演化模型;接着,开展Ti80低周疲劳实验,获得材料参数;然后,利用ABAQUS模拟Ti80合金的循环应力应变响应;进一步,基于本文的疲劳损伤累积模型,数值模拟Ti80材料损伤演化过程并预测材料的低周疲劳寿命;最后,将新的模型和经典的Lemaitre模型的预测结果与实验值进行比较分析。
1 考虑裂纹闭合效应的低周疲劳损伤分析
1.1 组合硬化模型
在预测疲劳寿命时,分析中的一个重要部分是材料的应力应变响应。通过实验观察,大多数金属材料在循环加载过程中都会出现某种程度上的循环硬化、循环软化、平均应力松弛等现象。而随动硬化和各向同性硬化的组合可以很好地描述循环加载下材料的循环硬化、循环软化、棘轮效应和平均应力松弛行为。因此本文将采用两者组成的硬化模型来描述钛合金的低周疲劳行为。
各向同性硬化表达式为[11]:
(1)

随动硬化表达式为:
σ*k=Ck(1-e-γΔεpl)/γk+σ*k,1e-γΔεpl
(2)
式中:σ*k为第k个背应力;σ*k,1为第k个背应力的初始值;Δεpl为等效塑性应变幅;Ck、γ为材料常数,Ck表示初始随动硬化模量,决定了材料在加载/卸载塑性阶段曲线的初始演化方向,γ表示随动硬化模量下降的变化率。该部分用于描述材料的包辛格效应、棘轮效应和平均应力松弛等行为。
1.2 考虑裂纹闭合效应的低周疲劳损伤累积模型
Kachanov[12]提出了连续损伤力学的概念,认为材料劣化主要是由于缺陷导致有效承载面积的减少,用连续度ψ来描述材料的损伤。随后,Rabotnov[13]做了进一步推广,引入损伤变量D。对于一维试件,损伤变量D表示为:
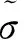

图1 拉伸与压缩时微裂纹的不同表现Fig.1 Different behaviors of microcracks between tension and compression
对于某些材料,在一定加载条件下,微缺陷在压缩时将发生部分闭合,缺陷面积与相同拉伸应力状态下不同,如图1(c)所示。由损伤的定义,材料相应的损伤也与受拉时不同。通常,将这一现象称为“微裂纹闭合效应”。为了考虑微裂纹闭合效应的影响,一般引入裂纹闭合参数h[9]。
因此,在受压状态下的有效承载面积为A-hAD,则有效应力为:
对于一般三维空间问题,一点的应力状态可以由3个主应力表示。为了方便讨论拉应力及压应力造成的不同影响,引入Mac Auley括号:
根据主应力的符号,把应力张量分解为正、负2部分:
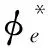
式中:ρ为材料密度;ν为泊松比。
进一步,推导出应变能释放率Y,它表示由于损伤而引起刚度损失所释放的能量:
对于拉应力状态,应变能释放率Y=Y+[14-15]:
式中Rv为三轴度,对于一维应力状态,Rv=1。
对于压应力状态,考虑材料中微裂纹的部分闭合,此时,应变能释放率Y=Y-:
低周疲劳损伤主要是材料在较高应力水平的循环载荷作用下,内部产生位错及滑移,在局部区域产生不可逆的塑性变形;随着塑性变形的不断累积,导致材料在局部区域产生微小裂纹,并产生持续的小裂纹聚合、扩展现象[16]。根据经典的Lemaitre低周疲劳损伤演化模型,假设每一循环过程中,疲劳损伤伴随着塑性应变而产生,将损伤统一动力律表示为:
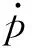
疲劳失效是一个能量耗散的过程。在低周疲劳损伤中,塑性变形是产生损伤的主要原因,而滞回曲线所围成的面积表示一个循环内的塑性耗散能。所以,在一维应力状态下,假设一个周期内的损伤不变,那么拉压与压缩下引起的损伤总和为:
为了便于计算,假定材料在一次循环中均完全塑性并具有门槛值分别为σs+=σeq,max,σs-=σeq,min。此时,考虑裂纹闭合效应的低周疲劳损伤演化为:
(3)
式中:σeq,max、σeq,min分别为峰值拉应力和峰值压应力;Δεp为一个循环内的塑性应变幅;基于式(1)和式(2)的组合硬化模型求解得到。
为了考虑临界损伤值Dc的影响,式(3)可以进一步修正为:
(4)
式中n为循环硬化指数。疲劳失效准则定义为:初始状态下,材料无损,损伤值D=0;随着循环次数N的增加,损伤逐渐累积;当D=Dc时,材料失效,其低周疲劳寿命为N=Nf。
2 Ti80合金低周疲劳实验
2.1 实验方法
为了获得组合硬化模型以及低周疲劳模型所需的材料参数,本文开展了Ti80合金的基本力学性能与低周疲劳实验。首先,根据GB/T 228—2002《金属材料室温拉伸方法》[17],在Instron 5982电子万能实验机上进行室温拉伸实验,拉伸速率为0.5 mm/min。其次,根据GB/T 15 248-2008《金属材料轴向等幅低循环疲劳实验方法》[18],在INSTRON 8801电液伺服疲劳实验机上进行应变疲劳实验。采用应变控制,应变比R=-1,应变速率为0.25%/s;共开展5组不同应变控制实验,每组设置3个平行试件,载荷大小分别为1.2%、1.0%、0.9%、0.8%和0.7%的总应变幅。当材料的峰值应力降低50%时,实验停止。
2.2 实验结果
单轴实验得到的应力-应变曲线如图2所示。

图2 单轴应力-应变曲线Fig.2 Uniaxial stress-strain curve
基于上述疲劳实验方法,分别获得不同应变控制下Ti80材料的峰值应力随循环次数的变化规律,见图3。由图3可知,在同一应变幅控制下,施加相同的拉伸与压缩循环载荷,材料产生的应力响应不同,其中,最大压应力大于最大拉应力,这表明材料在受拉与受压时产生的损伤不同。根据实验数据,拟合Ti80合金的材料参数如表1所示。
3 基于裂纹闭合效应的低周疲劳损伤分析方法
3.1 Ti80合金低周疲劳数值模拟
根据试样标距段尺寸建立1/4有限元模型,单元类型为轴对称单元CAX4R。将本文提出的低周疲劳损伤模型与失效准则编写到USDFLD子程序中,并将子程序嵌入ABAQUS,实现Ti80材料的低周疲劳损伤计算,当积分点的疲劳损伤达到阈值后,修改该积分点的杨氏模量为一极小值来模拟材料的劣化失效。

图3 各应变幅下Ti80合金的峰值应力与循环次数曲线Fig.3 Response curves of the peak stress with cycles at strain ranges of Ti80 alloy

表1 Ti80合金材料参数Table 1 Mechanical properties of Ti80 titanium alloy
3.2 Ti80合金低周疲劳损伤模拟结果
在应变控制下,基于组合硬化模型获得Ti80合金的应力应变历程,如图4所示。Ti80合金的应力应变一般在几个循环后趋于稳定,因此,当前仅展示前10个周期的滞回曲线。从图4中可知,不同应变幅下,外载荷越大,材料的塑性应变幅和拉、压峰值应力则越大;各载荷条件下单个循环的塑性应变幅和拉、压峰值应力与实验值均吻合较好。在线性向非线性过渡时,模拟的应力值偏高。这主要是在非线性随动硬化模型中取单级背应力的缘故。已有研究表明[19],单级背应力模型简单,并具有快速稳定的优势,但会导致背应力项离散。由于本文在计算损伤模型式(4)时,主要是基于各循环下的塑性应变幅与拉、压峰值应力,因此,由单级背应力引起的误差可忽略。

图4 各应变幅下Ti80合金的滞回曲线Fig.4 Hysteresis loops of Ti80 alloy at strain ranges
在数值模拟中,子程序调用单个循环内的拉伸、压缩峰值应力和塑性应变幅,然后根据式(4)进行损伤累积计算,当单元的损伤达到临界值Dc时,单元失效。不同应变幅下的损伤演化曲线模拟结果如图5所示。从图5中可知,在同一应变幅作用下,损伤随着循环次数的增加缓慢增加,材料的性能恶化也逐渐加快,在疲劳失效未期,损伤急剧增加,这是因为当微裂纹形成后,裂纹迅速扩展直至试件断裂;在不同应变幅作用下,外载荷越大,损伤累积速率越快,达到Dc所需的次数越少;此外,本文提出的考虑裂纹闭合效应的模型计算结果比Lemaitre疲劳模型计算结果更接近实验值,预测效果更好。

图5 各应变幅下Ti80的损伤演化曲线Fig.5 Damage evolution curves of Ti80 at strain ranges
当D=Dc时单元失效,对应的加载次数N为材料的失效寿命Nf,如表2所示。根据表2可知,新的模型比Lemaitre的低周疲劳模型预测效果更好,平均误差为5.24%,结果表明该模型能更准确地模拟Ti80合金材料的低周疲劳寿命。
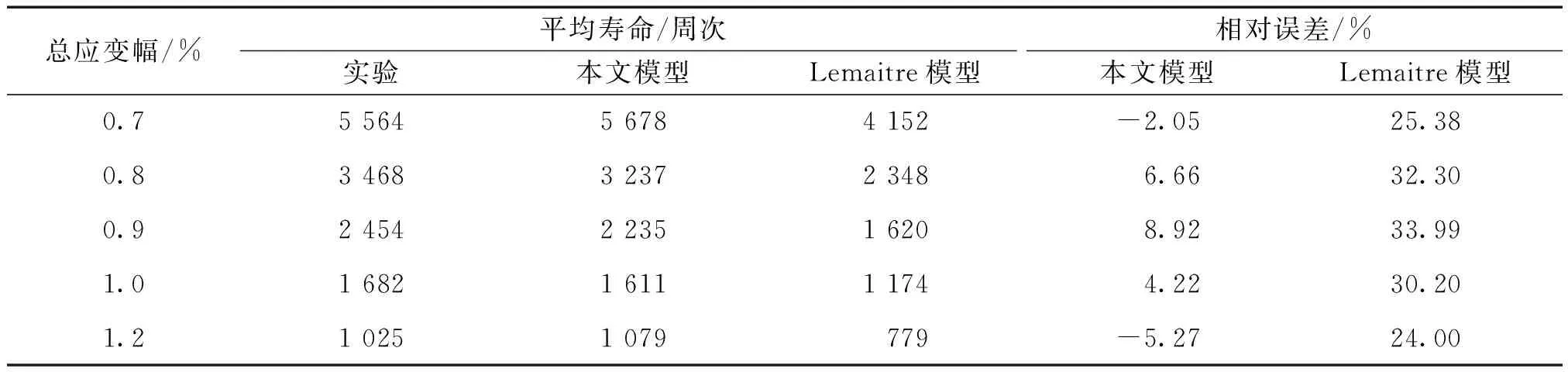
表2 不同应变幅下的实验寿命与预测寿命比较Table 2 Comparison of test life and predicted life under different strain amplitudes
4 结论
1)通过Ti80单轴低周疲劳实验可知,材料在相同的拉伸与压缩载荷作用下,产生的最大压应力大于最大拉应力,相应引起的损伤程度也不同。因此,在分析以受压为主的耐压壳体的低周疲劳损伤时,应考虑拉伸与压缩引起的损伤差异,即微裂纹闭合效应的影响。
2)通过数值模拟结果可知,假设拉伸与压缩损伤相同的Lemaitre模型模拟的损伤值高于考虑裂纹闭合效应的疲劳损伤模型,经过对比各应变幅下低周疲劳实验寿命和2种模型的预测寿命,可以发现本文提出的模型预测效果更准确,平均误差为5.24%。
