缓坡沙坝海岸波生沿岸流不稳定性特征

2022-08-17王彦朱雨昕刘忠波尹晶邹志利沈良朵

哈尔滨工程大学学报 2022年7期

王彦，朱雨昕，刘忠波，尹晶，邹志利，沈良朵

(1.大连海事大学交通运输工程学院, 辽宁大连 116026； 2.国家海洋环境监测中心，辽宁大连 116026； 3.大连理工大学海岸及近海工程国家重点实验室, 辽宁大连 116024； 4.浙江海洋大学海洋工程装备学院，浙江舟山 316022)

沿岸流不稳定运动对研究近岸波生流运动规律[1-2]、泥沙输运[3]和沙坝形成机理[4-5]等具有重要意义。沙坝又是近岸常见海底地貌特征，具有保护岸滩免受侵蚀的作用。沿岸流不稳定运动与韵律海岸[6-7]、裂流[8]、波浪爬高[9]等变化密切相关。因此进行沙坝海岸沿岸流不稳定运动研究是必要的。

Oltman-Shay等[10]通过现场观察首次发现了近岸破碎区域沿岸流存在周期O(1 000 s)、波长O(100 m)沿岸传播的蜿蜒波动，此波动与对应频率的重力波波长相比要小很多。Noyes等[11]在Duck、north Carolina的沿岸流现场实验中观测到沿岸流不稳定运动，通过分析流速时间历程来研究沿岸流不稳定运动的特性，结果表明剪切波主要发生在沿岸流最大值附近。Reniers等[12]通过对沿岸布置的12个流速仪采集到的流速时间历程进行频率波数谱分析，表明在陡坡沙坝地形下存在沿岸流不稳定运动，并基于线性不稳定理论计算了剪切波的色散关系及其与实验结果对比。任春平[1]应用最大熵谱分析了斜坡沿岸流实验的不稳定运动，给出2个坡度(1∶100和1∶40)斜坡地形不同波浪类型的波动周期。沈良朵[13-14]通过实验和数值模拟给出了缓坡平海岸沿岸流非线性不稳定特征。Tiessen等[15]数值研究了新月形沙坝特征演化和风暴潮后新月形沙坝在沿岸方向的空间尺度。以上研究主要关注陡坡海岸沿岸流不稳定运动或者沙坝剖面的形成机理和演化，而对于缓坡沙坝海岸情况沿岸流不稳定演化特性研究相对较少。

本文沿岸流不稳定实验研究是针对缓坡1∶100坡度缓坡沙坝海岸，通过沿岸流不稳定的谱特征和墨水运动所反映的沿岸流不稳定特征2方面，分析了缓坡沙坝海岸下沿岸流不稳定运动的特征，并讨论了沙坝对沿岸流不稳定特征的影响。

1 实验布置

实验在大连理工大学海岸及近海工程国家重点实验室的多功能水池中进行，水池长55 m、宽34 m、深1.0 m。沙坝海岸与造波机成30°。沙坝剖面采用高斯型，其中心距静水线7 m，宽为2 m，坝顶水深0.018 m。模型与周围三面水池壁都留有4.4 m宽的间隔，其水深与坡前平底处水深一致，实验会在沿岸方向水位差的作用下产生由沿岸流带动的水池内水体循环，如图1 所示。

表1 实验波况Table 1 Test conditions

图1 实验布置Fig.1 Experimental set-up

实验采用29个ADV流速仪安装在2个测量架上，分别测量垂直岸线和沿岸方向的流速时间历程。垂直岸线布置16个ADV用于测量沿岸流速度分布。流速仪端部与水底的间隙均为水深的1/3，以使测得的沿岸流更接近水深的平均值。实验中ADV 流速仪的采样频率为20 Hz，采集时间: 规则波采集时间为450 s，不规则波为700 s。需要说明的是由于不规则波相对规则波需要更长的时间来反映其不稳定波动特性。实验波面升高由60 个垂直于岸线方向排列的3列电容式浪高仪测量，列间距为5.0 m，布置如图1。

2 沙坝海岸沿岸流线性不稳定模型

沿岸流不稳定水动力方程是在文献[1]基础上增加了底摩擦项，建立基于波浪周期和水深平均的包含波浪驱动力项、侧向掺混项和底摩擦力项的水平二维近岸环流方程：

(1)

(2)

(3)

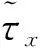
假定水平流速(u,v)包括平均沿岸流V(x)和扰动速度(u′,v′)，即v(x,y,t)=V(x)+v′(x,y,t)，u(x,y,t)=0+u′(x,y,t)，将其代入式(2)和式(3)，忽略非线性项和耗散项可得线性化后扰动控制方程：

(4)

(5)

(6)

式中：底摩擦系数μ=(2/π)fcwuwa，uwa为近底波浪水质点水平速度幅值。连续方程可简化为:

(7)

引入满足连续方程的流函数ψ：

(8)

并且将式(5)和式(6)分别对y和x求导相减，得到：

(9)

令式(9)解的形式为ψ=Re{φei(ky-ωt)}，φ为流函数的幅值，k为波动波数，ω=ωr+iωi，ωr和ωi分别为沿岸流波动的圆频率和不稳定增长率。将其代入式(9)即可得到沿岸流线性不稳定的控制方程：

(10)

式中:c=ω/k=cr+ici，cr=ωr/k即为沿岸流不稳定的相速度。

对式(10)只需给出平均沿岸流速度分布V(x)和h(x)，即可计算沿岸流不稳定的增长模式。本文采用光滑样条拟合对离散数据进行拟合得到的曲线，这样能够得到连续的数据并逼近实测的平均沿岸流速度剖面。图 2给出平均沿岸流的拟合结果。图2中，波况为MRT1H1,H0=3.08 cm，T=1.0 s。

图2 平均沿岸流速度剖面及样条拟合Fig.2 Longshore current and spline fitting curve

3 沿岸流不稳定特征分析

3.1 实验沿岸流的不稳定谱特征

本文采用最大熵谱法[1]对流速时间历程的稳定流速区域段进行分析。图3给出了波况为MRT2H1的流速最大值附近3个位置的流速时间历程来说明时间平均流速的分析过程。图3中也给出低通滤波截断频率为0.05 Hz的流速时间历程。由图3可以看出沿岸流在100 s时开始趋于稳定，150 s之后的流速已经稳定。当稳定沿岸流出现后，沿岸流流速历程出现较明显的周期性波动，垂直岸线方向流速时间历程的波动与沿岸方向的波动相似。其他波况的流速时间历程也是在150 s以后流速达到稳定状态，因此本文选取150 s后的流速时间历程进行谱分析处理。

图4仅给出了规则波波况(MRT2H1)和不规则波波况(MIT1H2)的沿岸流沿岸方向流速v的谱分析结果，图4中实线、虚线和点划线表示3组实验，选取了沿岸流速度剖面5个位置。沙坝内侧3个位置(x=4 m,5 m,6 m)，速度最大值位置(x=6.5 m )及沙坝顶(x=7 m)。图4中给出了线性不稳定计算模型计算得到的波动频率(用竖向粗虚线)。

沿岸流不稳定谱分析结果中存在多个峰值，这些峰产生的原因比较复杂。沿岸流不稳定运动大致分为3类：第1类是由线性不稳定引起；第2类是由非线性不稳定倍周期引起；第3类是由平均沿岸流沿岸不均匀分布或涡运动等引起[13]。

本文实验结果都属于第1类不稳定运动，这是因为实验谱分析的最大峰值和线性不稳定计算模型的波动频率吻合。不稳定谱分析结果存在多个峰，规则波情况(图4(a))：峰值较为集中，垂直岸线不同位置的波动周期在130 s左右。不规则波情况(图4(b))：谱峰能量相对分散，除了主峰之外，其他小峰值也较为明显，多个峰所在的频率呈现出倍频特征。谱分析结果表明，1∶100缓坡沙坝海岸沿岸流不稳定运动波动周期为100～150 s，且规则波情况的波动周期略大于不规则波情况。

图3 波况MRT2H1流速时间历程Fig.3 Time series for case MRT2H1

图4 沿岸流沿岸方向流速时间历程最大熵谱Fig.4 Maximum entropy spectrums of longshore current

表2给出第1类波动类型线性不稳定求得的波动周期与实验谱分析结果的比较。表2给出利用线型不稳定谱分析的波动周期是由图3中沿岸流最大值位置(x=6.5 m)最大熵谱曲线的谱峰对应的频率值求得的周期。由表2可以看出：所有波况的谱分析得到的沿岸流不稳定波动周期结果与线性不稳定理论计算得到第2个模式对应的波动周期较为接近，最大相对误差为13.1%(波况MRT3H2)，并且第2模式对应的为占优模式(即不稳定增长率最大模式)。可以表明此种情况的沿岸流不稳定运动处于线性不稳定发展阶段或者弱非线性不稳定阶段，即可用线性不稳定理论来分析本文1∶100坡沿岸流不稳定运动。

表2 第1类波动谱分析与线性不稳定的波动周期Table 2 Oscillating period between the results of linear theories and spectral analysis

线性不稳定第1个模式(非占优模式)对应的波动周期约为第2个模式(占优模式)结果的3倍，波动周期接近于300 s。进一步观察图3可看出，第1个模式(非占优模式)也起作用，在沿岸流不稳定运动中会产生相应的波动频率。例如不规则波波况MIT1H2的谱分析结果在由第1个模式对应的线性不稳定的波动频率f=0.003 2 Hz(T=312 s)处存在明显峰值，其他不规则波波况谱分析结果在由线性不稳定计算得到的第1个模式(非占优模式)对应的波动频率处也存在小的峰值，只是谱峰能量较小，没有充分发展起来。而对于规则波，由于采集时间仅为450 s，谱分析结果中不足以得到第1模式计算得到的不稳定波动周期(300 s左右)，所以在图3中与规则波情况第1模式计算得到的不稳定波动频率所对应谱峰不明显。

3.2 示踪墨水运动反映的沿岸流不稳定特征

本节通过同步记录墨水随时间运动所显示的不稳定波长和线性理论计算所得的不稳定波长进行对比，来反映沿岸流不稳定的特征。图5给出了波况MRT1H1和MRT1H2的墨水运动的实验照片，图5中从上至下依次是下凹、过渡、上凸、过渡和下凹图片来反应墨水波动现象。可以看出墨水在沿岸方向存在明显的波动，墨水出现上下摆动现象，图5中用双向箭头线给出了一个波动波长的范围。以波况MRT1H2为例，图5(b)给出了墨水发展的初始状态(t=60 s)，呈现下凹形式的波动；图5(f)给出了t=350 s时刻的墨水状态，呈现上凸形式的波动；图5(j)给出了t=510 s时刻的墨水状态，呈现下凹形式的波动；图5(d)、(f)是上凸下凹的中间过渡状态，从而形成一个完整的墨水上下摆动的过程。

表3给出线性不稳定计算得到的波长与实验中测量墨水运动所得出的不稳定波长比较，表3中波长是通过墨水运动照片确定的。表3第2列给出墨水的波动波长大约为8.1 m，而线性不稳定计算模型得到的不稳定波长为8.61 m，两者相差不大。表3中给出了沿岸流线性不稳定计算得到的波长与实验中测量墨水运动所得出的不稳定波长比较。通过墨水运动随时间演化的图片和线性不稳定理论计算所得的不稳定波长对比，沿岸流不稳定引起的沿岸流周期性摆动与实验中观测到的波动现象一致，两者波长相差不大，最大误差为16%(波况MIT2H2)。

4 沙坝对沿岸流不稳定运动的影响

通过对比沙坝和斜坡海岸[16]沿岸流不稳定特征,说明沙坝存在对沿岸流不稳定运动的影响。这一影响体现为沿岸流流速剖面具有以下2个不同于斜坡沿岸流的特征：1)速度剖面存在第2峰；2)速度剖面的最大峰值位置不同。沙坝的最大影响是控制着速度剖面最大峰值位置[17]，从而影响不稳定运动特征。表4给出斜坡[16]和沙坝海岸沿岸流不稳定运动第1类波动类型的实验谱分析和线性不稳定求得的波动周期结果的比较，第1类波动类型为谱分析波动周期和线性不稳定求得波动周期较为接近。通过对比可知：沙坝海岸情况谱分析得到的波动周期都小于斜坡情况。规则波波况，斜坡海岸波动周期为沙坝海岸的2倍左右；不规则波波况，斜坡海岸波动周期为沙坝海岸的4倍左右。

线性不稳定第1模式对应的波动周期与斜坡情况的相接近。2种地形不稳定波动周期存在差异的原因是沿岸流的不稳定性受到速度剖面的影响，而速度剖面受沙坝的控制。图6给出了沙坝海岸和斜坡海岸沿岸流的实验流速的拟合曲线对比。从图6中速度剖面拟合曲线对比可以看出，由于沙坝的存在控制着沿岸流的速度剖面峰值都出现在沙坝顶，这使得同一地形情况下沿岸流不稳定增长率曲线的最大峰对应的波数相差不大，从而使得沙坝海岸与斜坡海岸沿岸流不稳定运动波动周期存在差异。如规则波情况，沙坝海岸的沿岸流不稳定的波动周期要略小于斜坡海岸，而不规则波情况，沙坝海岸的沿岸流不稳定的波动周期接近斜坡海岸波动周期的30%左右。另外从墨水运动也可以看出(图5)：墨水的摆动受沙坝控制而不容易跨越沙坝离岸运动，这表明沙坝限制了沿岸流不稳定运动。