基于统一灰色生成算子的三参数离散灰色预测模型及其应用

李 惠, 曾 波, 苟小义, 白 云

(1.重庆工商大学 管理科学与工程学院,重庆 400067 2.重庆工商大学 工商管理学院,重庆 400067)

0 引言

灰色预测模型是灰色理论的重要组成部分，按变量个数可分为单变量灰色预测模型和多变量灰色预测模型两类[1]。单变量灰色预测模型通过灰色累加生成算子弱化原始序列随机性并挖掘其变化规律与演化趋势，具有变量个数少、建模过程简单等优点[2]，近年来得到了更为广泛的应用[3～6]。GM(1,1)模型[7]是邓聚龙教授最早提出的含一阶差分方程一个变量的灰色预测模型，是灰色理论预测分支的起点和基础。目前，GM(1,1)已成为一个重要的单变量灰色预测模型，被广泛应用于国计民生的多个领域[8～10]。

GM(1,1)本质上为齐次指数函数。然而，当建模序列严格满足齐次指数特征时，该模型同样存在模拟误差。谢乃明教授较早发现并对该问题进行了系统分析和深入研究，认为GM(1,1)模型参数估计源于离散形式的差分方程，而模拟和预测采用的是连续形式的微分方程[11]。从离散形式的估计到连续形式的预测这一变换过程存在模型机理误差。在此基础上提出了含一阶差分方程一个变量的离散灰色预测模型DGM(1,1)[12]。DGM(1,1)模型能实现对齐次指数序列的无偏模拟，是对GM(1,1)模型在建模机理方面的拓展和优化。

然而现实世界中，大多数时间序列呈现出非齐次指数的特点。在此情况下，DGM(1,1)固有的模型结构导致其面向非齐次指数序列时很难得到一个满意的预测效果。因此，曾波以DGM(1,1)为基础，通过引入线性灰作用量构建了一个含三个参数的离散灰色预测模型TDGM(1,1)[13]。该模型具有结构自适应性和面向齐次/非齐次指数序列及线性函数序列的无偏性，是一个性能良好的单变量灰色预测模型。

为了进一步提高TDGM(1,1)模型精度，何承香等[14]借助粒子群算法对模型参数，包括初始值、背景值系数及累加生成阶数进行了组合优化，从实际应用效果来看，该研究有效提高了TDGM(1,1)的综合建模性能。进一步研究发现，累加生成阶数对模型性能的影响大于模型初始值和背景值系数的影响，说明阶数是影响灰色预测模型性能的一个重要参数。

曾波等在文献[15]中提出了面向实数域的统一灰色生成算子，实现了累加生成阶数从R+到R的拓展，同时解决了灰色累加生成算子与灰色累减还原算子及灰色零化算子的统一问题，指出灰色算子阶数可小于0(r<0)，表示该算子具备挖掘时序数据差异信息的功能。然而，当前TDGM(1,1)模型中的灰色累加生成算子仍局限于正实数R+，其同等重要的序列差异信息挖掘功能未得到充分利用。

为此，本文借助文献[15]中面向实数域统一灰色生成算子的思想，对TDGM(1,1)模型的累加生成算子进行实数域拓展和优化，在此基础上构建了一个新的TDGM(1,1)模型，简称TDGM(1,1,r)，其中阶数r∈R。本文详细介绍了新模型的定义、参数估计方法、模型时间响应式和还原式的推导。本文通过构建TDGM(1,1,r)模型的某装甲装备维修费用预测模型，对该模型的有效性和实用性进行了检验，结果显示其模型综合性能优于其他同类单变量灰色预测模型。

1 灰色累加及累减算子的统一

传统灰色累加生成算子主要是挖掘原始序列增量信息的预处理工具，而其逆算子灰色累减算子则主要用于对累加后的模拟序列作还原处理。实数域灰色生成算子[15]通过引入实数δ将灰色生成算子的阶数近似地拓展到了实数域，从而实现了传统灰色累加生成算子及灰色累减生成算子的统一。

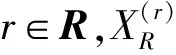
(1)

根据文献[15]可知，定义1中通过r的正负性可判断实数域灰色生成算子类型，其中，r>0对应累加算子；r<0对应累减算子，因而其具有更强的数据预处理能力。另一方面，r的正负性可判断实数域灰色生成算子的功能，具体地，当r>0，表示获取序列增量信息的功能；当r<0，表示获取差异信息的功能。因而其能有效满足不同实例情况下灰色生成算子对原始序列数据增量或差异信息的挖掘。因此，将实数域灰色生成算子运用到灰色预测模型的构建有益于挖掘模型预处理能力及拓宽模型作用空间的潜力。

2 面向统一灰色生成算子的三参数离散灰色预测模型

以灰色累加及累减算子的统一为基础，本小节引入实数域灰色生成算子，构建了预处理能力更强、作用空间更广的面向统一灰色生成算子的三参数离散灰色预测模型。

2.1 模型定义

(2)

为面向统一灰色生成算子的三参数离散灰色预测模型，简称TDGM(1,1,r)模型。其中，阶数r∈R，特别地，当r<0时，灰色生成算子对原始序列差异信息的挖掘功能在TDGM(1,1,r)模型中首次得以体现，有效增加了模型的作用空间和适应性。

2.2 模型求解方法

(3)

证明略。

(1)TDGM(1,1,r)的时间响应式为

(4)

(2)TDGM(1,1,r)的还原式为

(5)

3 应用举例：装甲装备维修经费预测

装备维修经费是用于武器装备维护、修理及维修器材、设备购置等相关保障活动的经费，是装备经费的重要组成部分[16]。装甲装备是装备维修经费按专业划分中的一项。目前，装甲装备维修经费存在发展趋势判断不准、经费标准不尽合理等问题[17]。预测装甲装备维修经费总量，可为装甲装备维修经费配置及管理提供科学依据。

表1 装备维修经费投入

以某单位 2010～2018 年装甲装备维修经费为例(数据来自文献[16]，详见表1)，预测该单位未来5年经费投入。针对该单位样本数量少及规律性不强的特点，构建了基于TDGM(1,1,r)的装甲装备维修经费投入预测模型。

具体地，选取前7个数据为建模序列，后2个数据为预测序列，其中,

=(593,586,…,1539)

使用MATLAB及PSO算法(MATLAB自带)构造TDGM(1,1,r)模型并得到最优阶数r*=-0.119996，表明当r*=-0.119996时，TDGM(1,1,r)模型对该单位装甲装备维修经费预测具有最佳的模拟性能。在本例中，r*=-0.119996<0，阶数r突破了传统灰色模型阶数取值为r>0的约束，表示灰色生成算子具备挖掘时序数据差异信息的功能，且对原始序列差异信息的挖掘功能得到了有效应用。

进一步，根据TDGM(1,1,r)模型可得到装甲装备维修经费模拟值/预测值，并可计算残差、相对模拟/预测误差。模拟/预测误差的公式如下:

(6)

为比较TDGM(1,1,r)模型中r取值不同对模型性能的影响，本文分别取r=r*,0.1,0.5,1对该装甲装备维修经费进行仿真，仿真结果见表2。

(7)

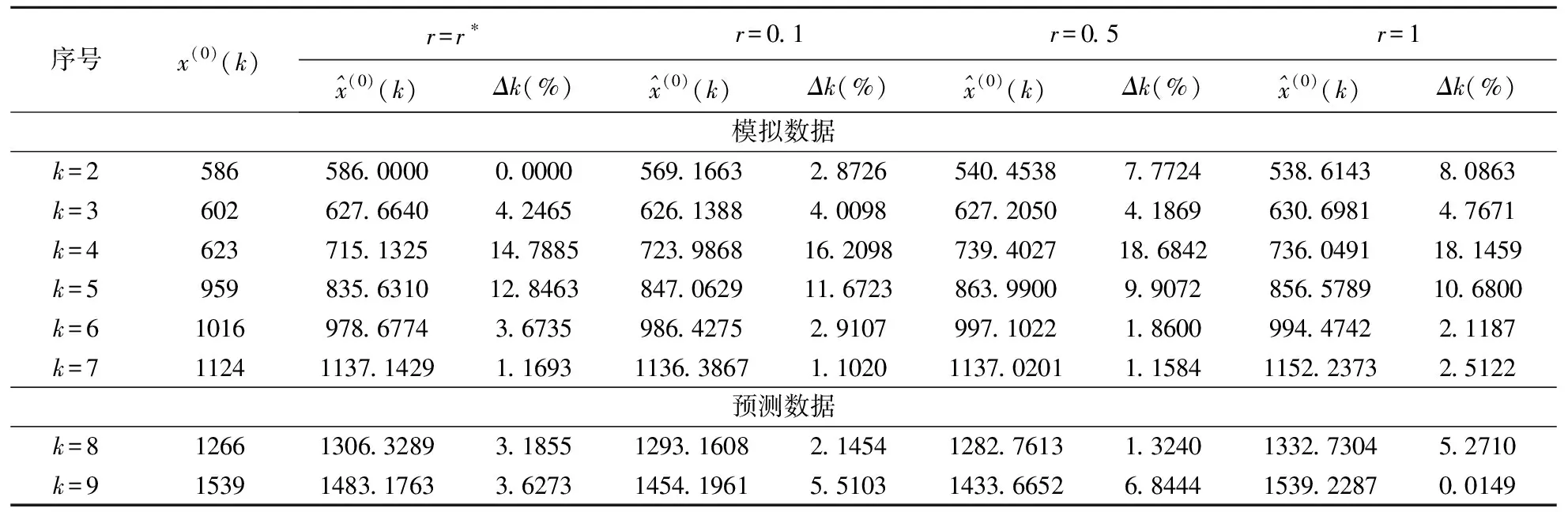
表2 不同模型对装甲装备维修经费的模拟与预测结果

表3 不同模型的误差对比

图1 不同模型误差柱状对比图

图2 装甲装备维修经费增长曲线图

为直观地对比不同模型的误差，根据表3计算结果绘制阶数取值不同所对应模型的误差柱状对比图，如图1所示。

根据图1可知，四种模型的平均相对预测误差柱状都较低，且r=0.1, 0.5, 1所对应模型的平均相对模拟误差及综合百分误差柱状图明显高于r=r*所对应模型。因此，r=r*时模型性能最佳。进一步，根据表3结果，r=r*时模型综合精度为94.56%，精度等级为II级，可用于预测。

应用TDGM(1,1,r)模型对该单位2019～2023年装甲装备维修经费投入进行预测，结果如表4所示。

根据表1及表4绘制2010～2023年装甲装备维修经费增长曲线图，如图2所示。

根据表4预测结果可知，到2023年，装甲装备的维修经费将近24+32万元，较2010年上涨3倍之多。同时根据图3，可以直观地看出历年来装甲装备维修经费投入总体呈现上涨趋势，特别地，装甲装备维修经费在未来五年的投入均较稳定的增涨，且增长趋势较往年平均趋势更为陡峭。该预测对未来装甲装备维修经费投入具有一定的参考价值，可为装备维修经费总量的投入、管理、分配提供科学依据，避免造成预算过度。

表4 2019～2023年装甲装备维修经费投入预测数据

4 结论

灰色生成算子挖掘原始序列增量信息的功能已得到大量运用，而其挖掘原始序列差异信息的功能未得到有效利用。为此，本文引入实数域统一灰色生成算子构造了面向r-RGO的三参数离散灰色预测模型，该模型中阶数的正负性可用于判定灰色生成算子功能，特别地，r<0表明灰色生成算子具有对原始序列差异信息挖掘功能，该功能在TDGM(1,1,r)模型中首次体现。将TDGM(1,1,r)模型应用于装甲装备维修经费的预测，结果显示灰色算子r<0,突破了传统灰色模型阶数取值r>0的约束，同时灰色生成算子挖掘原始序列差异信息的功能得到了有效应用。

本文通过构建新型灰色预测模型及案例应用验证了挖掘原始序列差异信息也是重要数据预处理手段。如何将灰色生成算子差异信息挖掘功能应用于其他灰色预测模型是本团队下一步拟研究的主要内容。