基于离散-连续耦合计算的露天矿边坡失稳特征与影响研究

田 涯，涂立啸，周 伟，王知乐，才庆祥，陆 翔

（1.中国矿业大学 矿业工程学院，江苏 徐州 221116；2.中国矿业大学 露天矿山高新技术研究中心，江苏 徐州 221116；3.中国矿业大学 煤炭资源与安全开采国家重点实验室，江苏 徐州 221116）

边坡安全稳定是露天矿重要研究课题，滑坡灾害发生将严重威胁人身安全与能源保障[1-2]。在实际生产过程中，企业往往会结合露天矿推进特点、空间形态，在规程要求范围内牺牲边坡部分稳定性以获取经济效益[3]、减少土地占用[4]。而降雨、冻融循环损伤、盐碱蚀破坏等环境因素对岩体力学性质的弱化不可忽略[5-7]，边坡失稳仍存在一定可能。边坡灾变过程的分析及滑体影响范围研究对矿山应急管理与风险管控有着重要意义。

露天矿滑坡的研究中，杨天鸿等[8]通过构建失稳案例等数据库结合岩体力学评价，从力学机理与案例匹配确定边坡位移时间序列阈值等，实现对滑坡预测预警；李聪等[9-10]同样以建立滑坡数据库的方式，归纳滑坡不同阶段变形特征、裂缝发育等信息来预测滑坡，并将滑坡演变过程分为初始变形、匀速变形、加速变形和急剧变形4 个阶段；王立文[11]通过边坡雷达监测获取抚顺西露天矿位移云图、速度曲线等变化规律，对边坡岩体变形阶段进行划分，通过速度阈值的设定对滑坡概率进行预测。在滑体形态研究中，王长军等[12]以南芬露天矿为背景，采用光滑粒子流体动力学方法（SPH）的数值模拟再现了老滑坡区松散堆积体复活过程，滑动距离、形态等呈现较好一致性，但研究是建立在边坡岩体和滑体力学强度差异较大且滑体形态已经给定的基础上，普适性相对较弱；霍文等[13]则采用离散元方法对典型岩质台阶破坏过程、剥离台阶与内排台阶安全距离等进行研究，与现场吻合度较好。在算法方面，有限元法或有限差分法基于连续介质假定，网格节点变形量受限，能够较好得对边坡应力-应变关系进行表述，但无法较好反应边坡位移、破坏的内容。离散元法对大变形问题有着较强处理能力，但计算过程要求颗粒数量繁多、颗粒间接触冗余，计算精度与时间均受限制。因此离散元对边坡研究往往集中在局部细节而非整体。

离散-连续耦合计算方法的出现一定程度弥补了离散元法与有限差分法的缺陷。研究表明耦合计算过程中边坡应力、位移在离散域与连续域有着较高一致性，离散域细观破裂机制可以有效表征边坡宏观塑性变形[14-15]。因此，以某巨厚煤层露天煤矿靠帮开采后端帮边坡为研究背景，潜在失稳区域采用离散元方法分析滑坡特征、破坏过程、影响范围等；基岩等变形量较小部分建立有限差分法网格，传递坡体内部应力、提高计算速度。

1 岩体宏细观力学参数

所研究露天矿煤层巨厚缓倾斜，地层倾向南东-南，生产能力30 Mt/a。该矿在靠帮开采后端帮帮坡角由28°提高至31.84°，已接近极限平衡状态。其中边坡高度257.12 m，煤层厚度74.55 m，地层逆倾6.42°，单台阶高度15 m、台阶坡面角60°。

通过钻探与现场踏勘将南帮地层主要分为第四系、灰色泥岩、泥岩、煤及灰色粉砂岩5 种，对煤岩试样进行单轴抗压强度试验与直剪试验，基于RMR评价法得到该矿岩体宏观力学参数[16]。离散元中，岩体所呈现出的宏观力学特性受离散单元间细观力学参数影响，通过室内试验所得到岩体力学参数无法直接应用于数值计算。常用方法是在离散元程序中复现室内试验过程，以试错法不断调整接触模型细观参数使数值计算与室内试验分别得到的应力-应变曲线相近，以此实现细观参数标定[17]。采用直剪试验获得岩体细观力学参数，剪切盒尺寸为30 m×30 m×30 m，颗粒数量107 202 个，颗粒半径660～1 000 mm（均匀分布），加载速度0.15 m/s。颗粒间接触默认为线性模型；颗粒胶结选用平行黏结模型，该模型黏结强度较高，能够承受弯矩等载荷，一般多用此模型模拟岩石、混凝土等材料。岩体宏细观力学参数见表1。

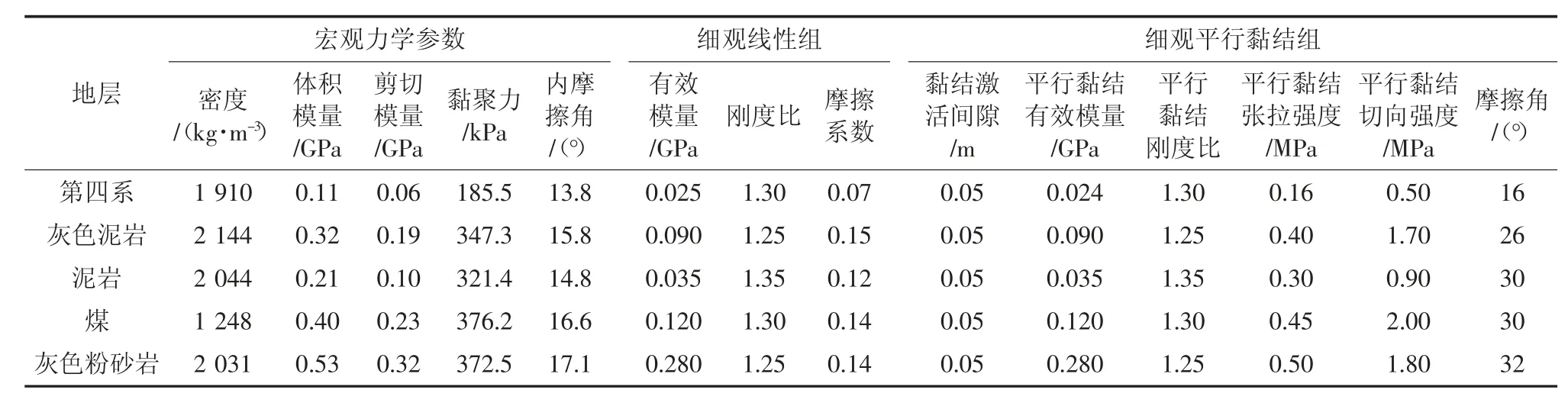
表1 岩体宏细观力学参数Table 1 Macroscopic and mesoscopic parameters of rock mass

2 基于有限差分法的南帮边坡分析

采用有限差分法对南帮端帮边坡进行分析,通过有限差分法的计算，初步得到了边坡失稳后的滑体范围、应力分布与位移等信息。端帮边坡屈服状态如图1，端帮边坡最大剪应变增量云图如图2，端帮边坡位移云图如图3。

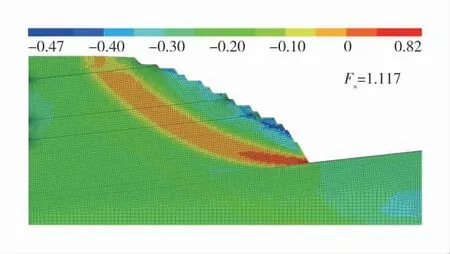
图2 端帮边坡最大剪应变增量云图Fig.2 Diagram of maximum shear strain increment of end slope

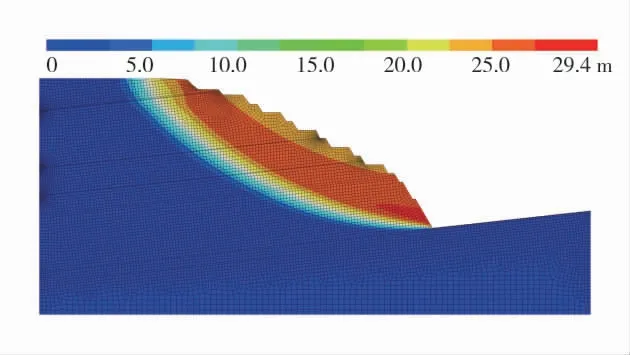
图3 端帮边坡位移云图Fig.3 Diagram of end slope displacement

图1 为边坡在强度折减算法计算结束后单元体的屈服状态，表示该区域岩体是否在应力作用下发生破坏，以及发生破坏的类型（红色部分指区域岩体正受剪切作用发生破坏、蓝色区域为单位正受张拉作用而破坏）。从单元区域状态可以看出，边坡潜滑面呈圆弧形，以剪切破坏为主，在滑体剪出口、滑体后缘处存在一定张拉破坏。其中，第四系地层受拉伸破坏最为明显，第四系下方的灰色泥岩一定程度阻碍了剪切破坏区域与张拉破坏区域进一步贯通。

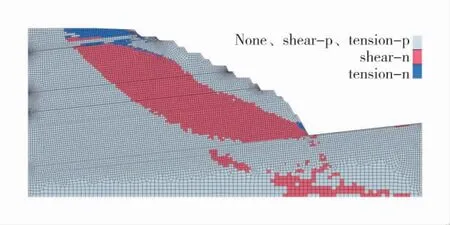
图1 端帮边坡屈服状态Fig.1 Yield state of end slope

图2 为边坡模型计算结束后最大剪应变增量云图，用来反映边坡潜滑面[18]。通过最大剪应变增量同样反映了端帮圆弧形滑动的趋势，但滑体范围相比图1 有一定收束。

图3 为边坡位移云图，滑体范围与最大剪应变增量所反映出的相近，坡脚处局部位移达到29.4 m。而限于程序连续介质的假定，该位移仅为不平衡力作用在单元体后应变增量的累加，参考价值较小。

3 离散-连续耦合计算方法和模型

3.1 计算方法概述

离散-连续耦合计算基于FLAC3D6.0 程序，该版本支持PFC 离散颗粒模型与FLAC3D连续单元模型之间物理力学信息进行传输与交换。其中，物理力学信息的传输、交换是通过在离散域与连续域之间生成“耦合墙体”，耦合墙体顶点与连续域单元节点重合。单元节点在不平衡力作用下产生位移，耦合墙体顶点记录位移过程并与单元节点保持同步，以此将连续域的信息传输至离散域中。离散元计算中，墙体运动对计算结果起到决定性作用。在连续域将单元节点的物理力学信息传递至耦合墙体顶点后，耦合墙体推动颗粒模型运动，运动后力学信息更新，墙体所受力与力矩通过等效力系统[19]分配至各个耦合墙体顶点，以此为媒介传递回连续域，此时1 个计算循环完成，程序最终通过显式积分得到耦合计算结果。离散-连续耦合计算过程如图4。

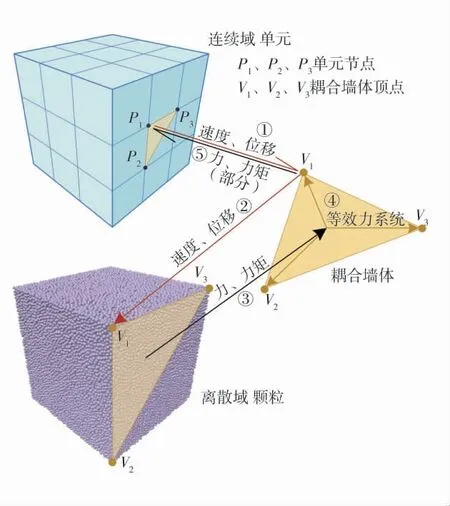
图4 离散-连续耦合计算过程Fig.4 Discrete-continuous coupling calculation process

3.2 耦合计算模型

以图1 的滑体范围为基准，向边坡内部偏移50 m，视为潜在的滑体范围。将范围内单元删除，替换为离散元模型，进行离散-连续耦合计算。耦合计算模型如图5，其中连续域内单元采用Mohr-Coulomb本构模型，离散域内颗粒接触采用平行黏结模型，黏结失效后退化为线性模型，滑体形态由有限差分法计算结果给出。计算模型长930.25 m、高410.80 m、厚度5 m，边坡参数与工程背景介绍相同。模型共生成单元14 924 个，颗粒302 298 个。

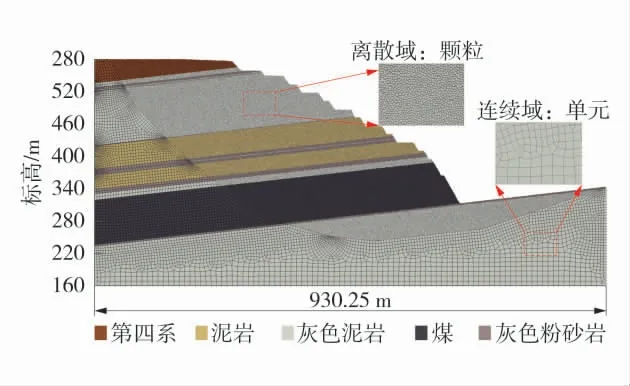
图5 离散-连续耦合计算模型Fig.5 Discrete-continuous coupling calculation model

3.3 强度折减法

通过折减岩体强度反复计算，使边坡达到临界破坏状态的方法称为强度折减法[20]。边坡在临界破坏状态时的强度折减系数视为其稳定性系数，是岩体原有力学强度和临界破坏状态强度的比值。该方法在有限差分法和离散元中均有研究[21-22]。通过有限差分法的计算已知边坡稳定性系数为1.117，为了分析边坡失稳过程的演化规律，且考虑到宏细观力学参数间存有一定偏差，故在耦合计算过程中对岩体宏细观力学参数进行1.150 的强度折减。

其中，有限差分法中强度折减法指边坡某单元岩体抗剪强度τ 为[21]：

式中：C 为岩体黏聚力，Pa；φ 为岩体内摩擦角，（°）；σ 为法向应力，Pa。

对岩体进行强度折减，折减系数为F，此时抗剪强度τF为：

4 基于离散-连续耦合计算法的南帮边坡分析

4.1 边坡位移演化

边坡水平位移演化过程如图6，边坡竖直方向位移云图如图7。

图7 边坡竖直方向位移云图Fig.7 Diagram of vertical displacement of slope

图6 可知，边坡水平方向位移演化呈圆弧形滑动，与FLAC 计算结果相近。随着计算步数的增大，端帮最大水平位移量不断增大。边坡受自重产生侧向变形影响，坡面颗粒最先出现黏结破坏，向下滚落并堆积至坡脚，滚落颗粒最大位移值超过40 m。计算至4 000 步时（图6（b）），受自重影响，滑体滑移，后缘出现张拉裂缝。边坡水平方向位移在5～10 m，坡顶裂隙和坡脚水平位移明显，呈现圆弧形滑动趋势。8 000～24 000 步时（图6（c）～图6（g）），边坡各区域位移随着计算步数增大，其中水平位移大小一定程度与岩性有关，能够体现边坡滑体非均质特性。坡脚和520 m 水平的位移增幅较大，边坡滑体清晰，坐落明显，下部滑体向临空面推挤，具有一定倾倒趋势。计算结束时（图6（h）），滑坡过程中煤台阶与灰色泥岩部分破坏严重，近似为2 个圆弧形滑面。中部灰色粉砂岩灰色泥岩互层在一定程度阻碍了上下2 部分滑面的贯通。与边坡初始轮廓对比，边坡整体破坏严重，原布置于端帮的各运输通道均存在较大变形。

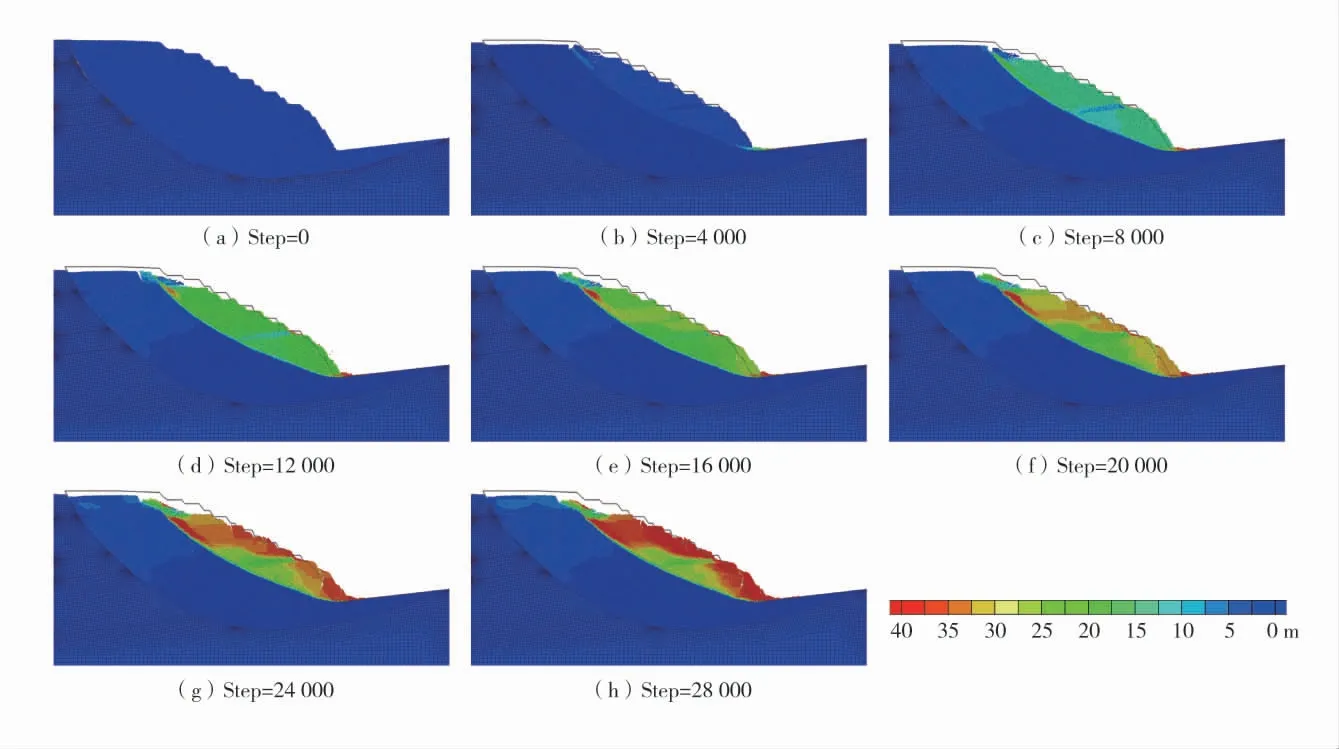
图6 边坡水平位移演化过程Fig.6 The evolution of horizontal displacement of slope

由图7 可知，由最下部煤台阶裂隙，边坡滑体可大致分为2 个部分。滑体在沿滑床向外剪出时，受坡脚颗粒堆积与逆倾构造影响而出现较大错动，滑体大致分为上下2 个部分。其中上部分滑体后缘竖直位移较大，在25～45 m 之间，接近滑面处位移较大，上部分滑体竖直位移在向中部过程中逐渐减小直至滑体前缘；滑体前缘受下部煤层错动影响，滑体前缘呈楔体向下滑移，位移在20～25 m 之间。下部分滑体位移较小，逆倾构造阻碍了下部分滑体进一步运动，对滑坡影响范围起重要作用。

4.2 边坡破坏过程

边坡破坏过程如图8。

由图8 可知，随着计算步数增大，边坡破坏的岩体数量、破坏程度增大。在计算至4 000 步时（图8（a）），边坡开始显现圆弧型滑动趋势，岩体较明显但相对完整，破碎岩体数量为2 453；12 000 步时（图8（b）），下侧岩体破坏严重，破碎岩体数量增幅较大，此时上侧岩体相对完整，煤层及顶板有加剧破坏趋势，破碎岩体数量增加至3 398；20 000 步时（图8（c）），下侧岩体破坏趋向稳定，上侧岩体逐层破坏，破坏区域上移；计算结束时（图8（d）），破碎岩体数量为4 412。

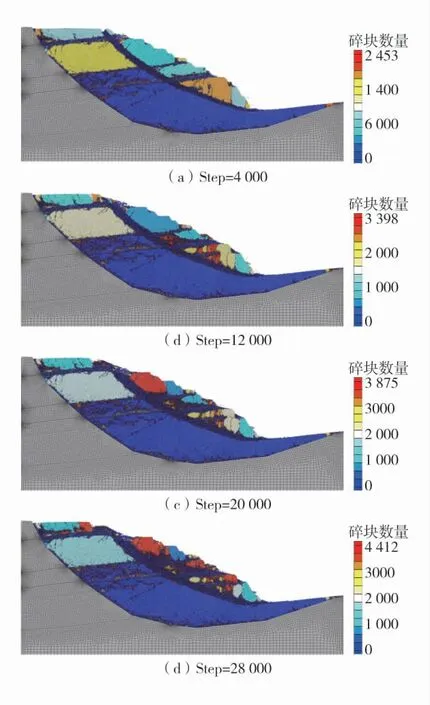
图8 边坡破坏过程Fig.8 Slope damage process

4.3 边坡失稳影响范围

边坡失稳影响范围如图9。

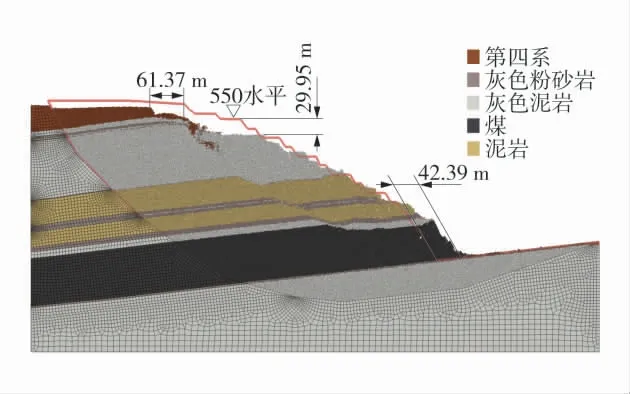
图9 边坡失稳影响范围Fig.9 Impact scope of slope slide

图9 可知，在滑坡过程中，最上部580 m 水平出现拉裂缝，距坡肩61.37 m 内有明显下沉，550～580 m 水平滑塌约30 m。边坡岩层错动明显，下部煤台阶及顶板向临空面处推挤，下部水平位移达42.39 m。通过耦合计算结果，初步给出了所述边坡在滑坡灾害发生后将影响的范围，为应急疏散及边坡安全距离确定提供一定参考。

5 结 语

1）通过室内试验与离散元数值模拟得到所研究边坡岩体的宏细观力学参数，通过有限差分法软件FLAC 计算得到连续介质下边坡滑体的范围。在此基础上建立边坡离散-连续耦合计算模型，以离散元方法建立潜在失稳区域模型，以有限差分网格建立基岩等模型，计算得到滑面位置与有限差分法近似。

2）离散-连续耦合计算得到边坡呈圆弧形滑坡，滑坡过程最先为坡面颗粒黏结受侧向变形影响发生少量破坏，黏结破坏后颗粒向下滚落并堆积在边坡坡脚；随后滑体后缘出现张拉裂缝，滑面逐渐清晰，滑体前缘煤层错动，并在边坡逆倾构造影响下阻碍滑坡进一步发展。

3）滑坡过程中滑体破坏严重，其中下侧岩体优先破坏，集中在煤层及顶板处，随后破坏区域上移，上侧岩体逐渐破坏。滑坡结束后，边坡最上部580 m水平出现较多张拉裂缝，距坡肩61.37 m 内有明显下沉，约为30 m。边坡岩层明显错动，下部煤台阶及顶板外临空面推挤，下部水平位移达42.39 m。

4）离散-连续耦合计算能够有效分析边坡大变形问题，有着较高计算效率。计算初步给出了边坡滑坡发生后将影响范围，能够为矿山应急疏散及边坡安全距离确定提供一定参考。但限于时间与技术能力，仅在二维层面对边坡滑坡特征及影响进行分析，未能体现露天矿工作帮与内排土场对端帮的支撑；采用强度折减法对边坡岩体粘聚力与内摩擦角同时折减，未能体现特定环境对力学参数的不同影响。以上内容将在后续研究中陆续完善。