基于改进SPSO 算法的开采沉陷预测参数反演研究
2022-08-16徐可心白伟森
徐可心,何 荣,白伟森
(河南理工大学 测绘与国土信息工程学院,河南 焦作 454000)
煤矿地下开采造成地表移动形变,引起地表裂缝、建筑物损害等,部分地区出现积水、水土流失等地质灾害,严重破坏矿区的生态环境。因此,有必要通过对矿区地表形变监测,获取变形数据、求算相关参数,总结地表移动盆地的变形规律,为维护矿区经济可持续发展及生态文明建设提供基础数据支撑[1]。
概率积分法是我国目前开采沉陷领域科学研究常用方法之一[2],构建了地表变形与地下开采空间的关系模型。不同的开采方法和地质采矿条件,预计参数具有较大的差异性,因此,科学确定预计参数大小对地表变形量计算至关重要。其参数求算主要有特征点求参、曲线拟合和曲面拟合等方法,曲面拟合法将曲线拟合法求参的原理推广到整个下沉盆地,充分利用非主断面地表变形监测数据,得到更加精确的地表移动变形参数值[3]。李春意[4]等将曲面拟合法用于求取矩形工作面的概率积分法参数,并验证了非线性曲面拟合法用于开采沉陷预计的实用性。该方法不要求观测站位于下沉盆地的主断面上,是非主断面设站求取概率积分法参数的主要方法。但其对初值选取要求较高,工作量大、求参速度慢。随着计算机技术的发展,为提高参数反演的效率,不少学者将智能算法应用到了概率积分法反演参数的研究中,优化算法有模矢法[5]、遗传算法[6]、果蝇算法[7]、神经网络算法[8]以及粒子群算法[9]等。与其他的寻优算法相比, 粒子群算法拥有较好的收敛能力,计算速度更快[10]。徐孟强[11]等首次将粒子群算法引入了概率积分法参数反演,认为粒子群算法可以有效解决随机误差和测点缺失的问题,存在全局搜索能力差、容易提前收敛等问题;叶伟[12]等将自适应鱼群算法用于曲面拟合求参,得到了较为可靠的拟合下沉曲面,所用方法运算复杂、计算效率较低。
基于此,针对传统粒子群算法存在的局限性,使用改进标准粒子群算法,进行曲面拟合概率积分法参数反演,计算参数拟合中误差和下沉拟合误差,验证改进标准粒子群算法用于概率积分法参数反演的有效性。
1 基于非主断面设站的曲面拟合模型
相比主断面设站法,非主断面设站具有布设灵活的特点,既方便观测,又减少了对农田的影响,被广泛用于矿区的地表变形监测。观测站位置的选取对参数反演精度有较大影响,为保证计算精度,观测站应尽量布设在变形值较大位置,或下沉盆地的特征点处[13]。
1.1 工程实例概况
试验区位于河北省邯郸市某矿,区内地形为低丘陵,地势南高北低,有较浅冲沟,部分有基岩出露。2516 工作面位于205 采区运输下山北翼,北面为充填集中轨道巷,西面为已开采的其他工作面,东南方向为村庄。工作面开采条件见表1。

表1 工作面开采条件Table 1 Mining conditions of working face
为监测矿区的地表移动变形,2516 工作面上方布设了走向与倾向2 条观测线,受地表村庄分布和地形限制,以非主断面设站法布设。观测线布设和井上下对照图如图1,走向观测线长671 m,共布设17 个水准观测点,倾向观测线长1 167 m,共布设28 个水准观测点。2516 工作面共进行5 次观测,其中走向最大下沉点下沉值为572 mm,倾向最大下沉点为走向与倾向观测线交点,下沉值为556 mm。
1.2 曲面拟合法函数模型
曲面拟合法不受观测站布设方法限制,但仅适用于矩形工作面。由图1 可知,2516 工作面为非主断面设站的矩形工作面,可使用曲面拟合法反演概率积分法参数。由概率积分法可知,矩形工作面下沉盆地内曲面拟合任意点下沉的函数W(x,y)为:
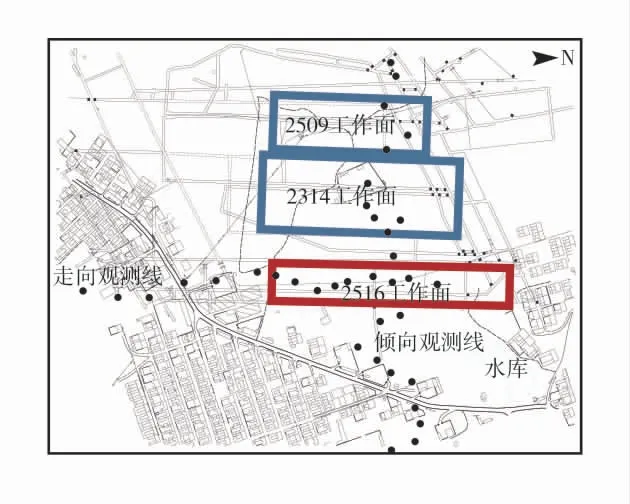
图1 地表移动观测站布设与井上下对照图Fig.1 Layout of surface movement observation stations and comparison between upper and lower wells

式中:W0为实测最大下沉值,mm;H 为走向主断面平均采深,m;H1、H2分别为下山和上山方向的采深,m;β、β1、β2为主要影响角,(°);D1、D3为矩形工作面倾向和走向主断面宽度,m;S1、S2分别为上山和下山方向拐点偏移距,m;S3、S4分别为走向左和走向右拐点偏移距,m;θ0为开采影响传播角,(°);α 为煤层倾角,(°)。
2 基于改进SPSO 算法的概率积分法参数反演
2.1 改进SPSO 算法
粒子群优化算法(Particle Swarm Optimization,PSO)是1 种群智能优化算法,源于对鸟群社会行为的研究。Reynolds[14]于1986 年设计了1 个再现鸟群聚集行为的人工生命系统,随后Eberhart 和Kennedy[15]基于该系统提出了粒子群算法。Y. Shi[16]等学者引入了惯性权重ω,并修正了粒子速度公式,引入ω 的粒子群算法被称为标准粒子群算法(Standard Particle Swarm Optimization,SPSO)。
假设在D 维的搜索空间中,N 个粒子组成1 个群体,第i 个粒子的位置表示为xi=[xi1,xi2,…,xiD],其飞行速度表示为vi=[vi1,vi2,…,viD],当前搜索到的最优位置为pi=[pi1,pi2,…,piD],整个群体当前搜索到的最优位置为pg=[pi1,pi2,…,piD]。由此得到粒子速度与位置的更新公式:


惯性权重ω 是SPSO 算法的重要参数,用于控制算法开发和搜索能力。当ω 取值较大,算法全局寻优能力较强,局部寻优能力较弱;当ω 取值较小,正好相反。在算法搜索过程中将ω 设置为动态,可以平衡收敛速度和搜索能力,使算法优化结果更精确。
PSO 算法的优势在于收敛能力较好,但面对复杂多维问题,PSO 算法常出现早熟,即提前收敛陷入局部最优解[17]。针对PSO 算法容易早熟的问题,在SPSO 算法的速度更新公式中引入渐进收敛的方法,改善算法全局收敛性,提高算法搜索能力。改进SPSO 算法粒子速度迭代公式为:

2.2 基于改进SPSO 算法的概率积分法求参模型
由式(1),可将下沉盆地内地表任意点的下沉值WPos表示为:
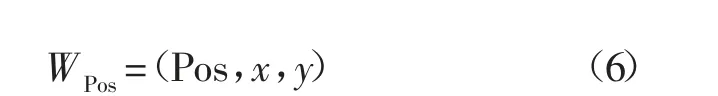
式中:Pos 为概率积分法的参数矩阵,Pos=[q,tanβ,tanβ1,tanβ2,S1,S2,S3,S4];q 为下沉系数;(x,y)为观测点坐标。
基于改进SPSO 算法的概率积分法参数反演流程如图2。

图2 SPSO 算法概率积分法参数反演流程Fig.2 SPSO algorithm probability integration method parameter inversion process
在改进SPSO 算法中,应先设置算法参数,确定适应度函数,然后通过迭代得到最优解,反演流程的具体步骤如下。
1)初始化种群。设置最大迭代次数、自变量个数、粒子的最大速度以及粒子约束条件为搜索空间,在速度空间和搜索空间上初始化粒子飞行速度和位置,设置种群规模,生成初始群体。使用MATLAB 语言对求参模型进行编程,假设空间内共有100 个粒子,学习因子c1=c2=2,nmax=500。粒子维数由所求公式参数数量决定,概率积分法参数矩阵中有8 个参数,分别为:下沉系数q,主要影响角正切tanβ、tanβ1、tanβ2以及拐点偏移距Si(i=1,2,3,4),确定粒子维数为8。为平衡算法搜索能力,设置惯性权重随迭代次数增加线性递减,令ωmax为0.9,ωmin为0.4。鉴于工作面实际情况,结合矿区现有岩移参数,确定粒子约束条件,即参数取值区间,参数取值上下限见表2。

表2 参数取值上下限Table 2 Upper and lower limits of parameter values
2)定义适应度函数。粒子每更新1 次位置就计算1 次适应度值,适应度值反应粒子的优劣程度。根据误差平方和最小原则,预计值和实测值之差的平方和越小,参数反演精度越高。构建适应度函数为:

式中:RSS 为拟合值与实测值之差的平方和;m为观测点总个数;Wi为实测下沉值,mm;wi为拟合下沉值,mm。
3)根据式(3)、式(5)更新粒子的速度和位置,并处理超出约束条件的粒子。迭代过程中,粒子通过个体极值和群体极值更新速度和位置。个体极值为每个粒子找到最优解,从个体最优解中找到全局最优解,与历史全局最优解进行比较,不断更新得到最终结果。
4)当相邻2 代全局最优解之间的偏差最小,或循环达到最大迭代次数时,循环终止,输出反演参数。在本研究构建的模型中,当相邻2 代全局最优解适应度值差值为0 时,认为找到最优解,或迭代次数达到500 次时循环停止。一般情况下迭代次数越多精度越高,但多余迭代次数会降低运算效率,为避免无效迭代并保证运算精度,通过试验确定最大迭代次数为500。循环停止输出最优解,即反演所得概率积分法参数。
3 基于改进SPSO 算法的模型在工程中的应用
3.1 参数反演结果
以2516 工作面实测下沉数据为基础(图1),分别使用改进SPSO 算法和PSO 算法进行参数反演,对比其求参结果和拟合中误差。为避免试验偶然性,2 种算法以相同设置各进行10 次试验,取试验结果的平均值为参数值,所得结果和矿区经验值见表3。矿区经验值参考205 采区已有地表移动变形参数,结合2516 工作面开采技术确定。

表3 反演参数对比Table 3 Comparison of inversion parameters
由表3 可知,除主要影响角正切tan β 外,改进SPSO 算法反演参数拟合中误差均小于PSO 算法反演参数拟合中误差,即改进SPSO 算法反演参数波动性小于PSO 算法,证明改进SPSO 算法稳定性优于PSO 算法。
3.2 可靠性分析及收敛速率比较
改进SPSO 算法和PSO 算法的迭代次数对比如图3,在算法10 次运算过程中,改进SPSO 算法出现1 次收敛过快未求得最优解,PSO 算法出现3 次。且改进SPSO 算法的平均迭代次数为47.3 次,PSO 算法平均迭代次数为300.4 次。可以看出改进SPSO 算法收敛速度远高于PSO 算法。

图3 迭代次数对比Fig.3 Comparison of iteration times
为分析改进SPSO 算法反演概率积分法参数的效果,将改进SPSO 算法和PSO 算法反演参数值和矿区经验值分别代入概率积分法公式得到拟合下沉曲面,与实测数据对比,并计算其拟合误差。
下沉拟合误差计算公式为:

由式(8)得,改进SPSO 算法反演参数拟合误差σ=4.66%,PSO 算法拟合误差σ=4.67%,矿区经验值拟合误差σ=10.2%。改进SPSO 算法反演参数精度和PSO 算法相当,高于矿区经验值。改进SPSO 算法反演参数和矿区经验值拟合下沉曲面如图4。算法拟合下沉值及实测值对比如图5。
由图4 可知,改进SPSO 算法反演参数拟合下沉曲面更接近实际下沉盆地的形状,拟合效果较好。由图5 可知,工作面走向方向拟合效果较好,倾向方向的部分监测点实测值大于拟合值。由图1 可知,2516 工作面西侧为2 个已开采工作面,且与2516工作面相距较近,2516 工作面的开采势必会引起老采空区的活化。根据覆岩“活化”机理[18],老采空区会因为上覆岩层的“活化”而产生二次破裂,造成地表下沉值大于预计值。试验反演概率积分法参数仅考虑单一工作面开采条件,2516 工作面在实际开采过程中受到了2314 和2509 已采工作面的影响,使得倾向观测线上山方向部分监测点拟合效果不理想。

图4 下沉拟合曲面及实测值对比Fig.4 Subsidence fitting surface and comparison of measured values
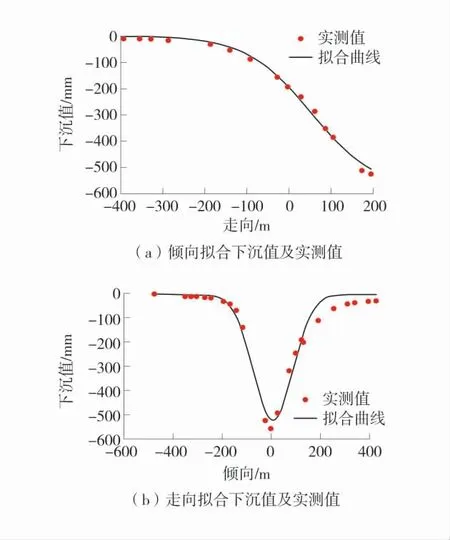
图5 算法拟合下沉值及实测值对比Fig.5 Algorithm fitting sinking values and comparison of measured values
为进一步分析改进SPSO 算法反演概率积分法参数的可靠性,基于改进SPSO 算法的反演参数值和概率积分法原理,对2516 工作面地表移动观测站的倾斜和曲率变形进行了预测。算法预计值与实测值对比如图6。
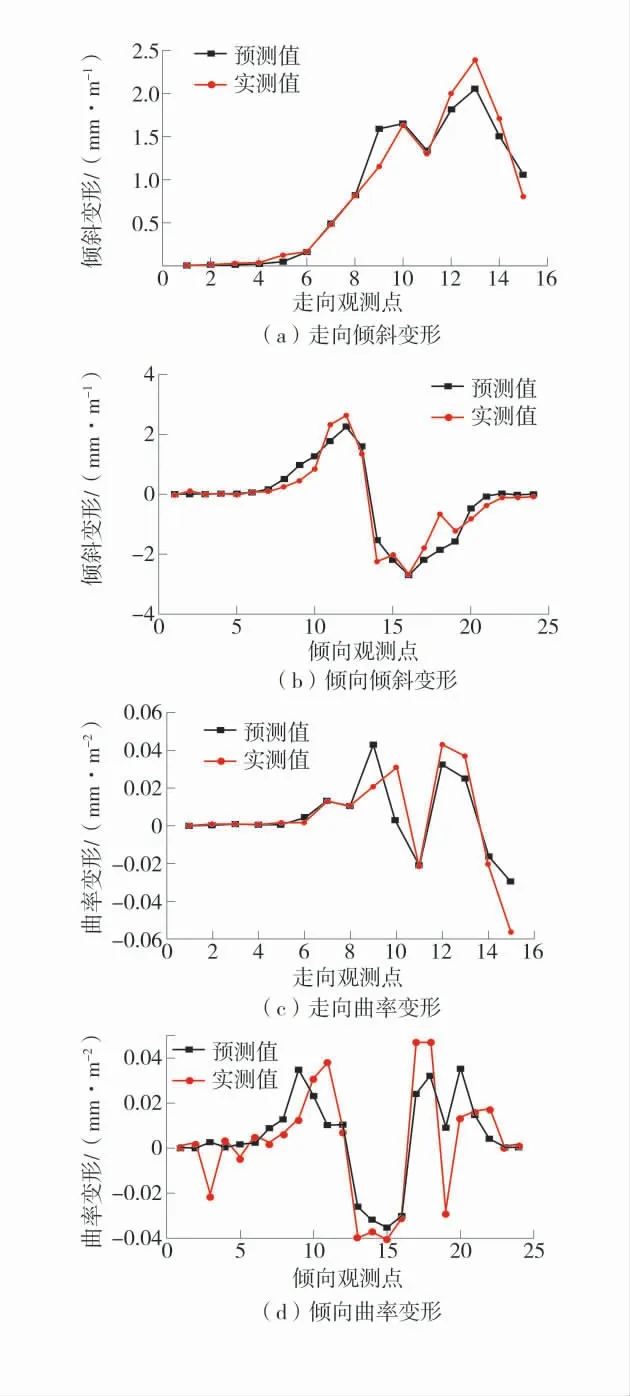
图6 算法预计值与实测值对比Fig.6 Comparison between the predicted values of the algorithm and the measured values
由图6 可知,算法倾斜及曲率变形预计值和实测值相比,整体变化趋势基本一致,除少部分异常点外,整体误差较低,预计效果较好。证明改进SPSO算法反演参数具有较高可靠性。
4 结 语
1)针对非主断面设站反演概率积分法参数的问题,将渐进收敛引入SPSO 算法,建立了基于改进SPSO 算法的概率积分法参数反演模型。研究表明,该方法参数反演运算效率高、拟合效果较好,通过该方法反演的参数具有较高可靠性。
2)反演参数值拟合中误差和下沉拟合误差的对比分析表明,改进SPSO 算法反演参数拟合中误差整体优于PSO 算法,参数反演精度高于矿区经验值,有效提高了参数反演准确性。和PSO 算法相比,改进SPSO 算法具有更好的收敛能力和稳定性。
3)由下沉、倾斜、曲率预计值与实测值的对比分析可知,改进SPSO 算法反演参数预计的拟合下沉盆地比较符合实际情况,对于提高矿区开采沉陷预计精度有一定的参考价值。
