云模型双重积分算子的层次多属性决策方法

王铁旦，张雨晴，彭定洪

昆明理工大学 管理与经济学院 质量发展研究院，昆明650093

由于社会环境的复杂性和人类认知的有限性，大多数决策问题所涉及的信息往往是不确定的，很难用精确的数值来表示，李德毅在经典的模糊数学和概率统计的基础上引入了云模型理论，云模型的突出优势在于隶属度的随机性以及考虑了随机性和模糊性之间的内在关系，其通过期望、熵和超熵三个数值特征来表示决策信息的模糊性、波动性和随机性。因此它具有一定的客观性，在一定程度上可以解决信息收集过程中的丢失问题。由于云模型具有的独特优势，其已经在多属性决策、智能控制、数据挖掘等领域得到了广泛应用。关于云模型的大量研究表明，云模型理论已成为解决不确定性的强大工具。此外，面对实际决策中的复杂问题，可能需要在层次结构中构造指标，通常的层次结构中较高层的指标依赖于较低层的指标，如果问题被构造成层次结构，那么在指标之间进行权衡的过程就会更加清晰。

目前解决具有层次结构决策问题的方法主要分为两类：一类是以层次分析法、层次Choquet 积分、分层TOPSIS 法为代表的多属性决策方法；另一类是在层次结构下运用聚合算子对各指标值进行聚合的方法。由于系统往往由许多相互关联、相互制约的因素组成，用聚合算子集结各指标的评价值更加具有优越性，聚合算子在具有层次结构的多属性决策问题中起着重要作用，其用于将部分子问题聚合为总体评价，运用聚合算子对模糊的评价信息进行处理，可有效避免原始信息的失真。

纵观当前云模型聚合算子的相关研究，Liu 等提出了基于语言术语的云模型转化方法，并构建了一系列云距离聚合运算符如云广义加权平均距离算子（cloud generalized weighted averaging distance，CGWAD）等；Wang 等将语言变量转换为云，然后提出了云加权算数平均算子（cloud weighted arithmetic averaging，CWAA）、云有序加权算数平均算子（cloudordered weighted arithmetic averaging，COWA）和云混合算术算子（cloud hybrid arithmetic，CHA）。以上所提出的云模型聚合算子只考虑了指标相互独立的情况，而在实际的决策问题中，决策指标之间不可避免地存在相互作用。为了解决这项问题，在不确定环境中指标具有关联性的前提下，许多学者开始基于模糊集理论与Choquet 积分构建了一系列聚合算子用于多属性方案的决策。在处理指标间具有联系性的多属性决策问题上，Choquet 积分是一个非常有用的工具，它的优势是不仅可以处理多指标的交互，而且还描述了复杂和非线性的相互作用。然而，在多属性决策问题中不仅指标之间具有复杂的关系，还需衡量权重与指标值的侧重关系。Sugeno 积分具有折中特点，可以做到既考虑指标权重，又考虑指标评价值，它会在集合的可靠性与集合元素分配的重要性之间进行权衡（或折中），同时也是解决多属性决策问题中计算平均整体得分的重要汇总工具。双重积分算法结合了Choquet积分和Sugeno 积分的优点，不仅考虑了指标之间的交互性，而且还涉及到了指标值与权重的侧重关系。

综合以上分析，在具有层次结构的不确定决策问题中，考虑到决策信息的模糊性和随机性，以及模糊测度在解决评价指标之间具有交互现象决策问题的可靠性能，本文用云模型来表示决策值及模糊测度，且进一步构建了一种云模型双重积分算子（cloud model twofold integral，C-TI），并基于该算子提出了具有层次结构的多属性决策方法，最后用于解决企业社会责任的评价问题，力求最大程度地消除决策者在评价过程中的失真，提升决策结果的准确性。

1 预备知识

1.1 云模型

李德毅等在概率论和模糊理论的基础上提出了云模型，云模型的三个数字特征可以实现定性与定量之间的转化，其中期望代表了最能反映所要表达的定性概念的定量值，熵反映随机性与模糊性之间的关联度，超熵体现了样本出现的随机性和云滴的凝聚度。

1.2 双重积分

Torra在2005年将Choquet积分和Sugeno积分结合定义了双重积分，双重积分体现了Choquet 积分处理交互问题的特点以及Sugeno 积分计算整体得分的优势。

定义4令为一个有限集合，设为幂集映射到[0,1]的可测函数，μ和μ为上的两个模糊测度，则关于模糊测度μ和μ上的离散双重积分定义为：

2 云模型双重积分算子及性质

利用云模型和双重积分的特点，并通过上文分析得出的结论，构建一个新的聚合算子——云模型双重积分算子。本文还给出了相应的云模型模糊测度，进一步体现出多属性决策问题中不仅在得出指标评价值时会出现模棱两可的情况，而且在判断指标权重时也会由于决策者对指标的认识不同而出现不确定的状况。下面给出具体定义。

2.1 云模型模糊测度

则称为云模型模糊测度。若云模型模糊测度满足：

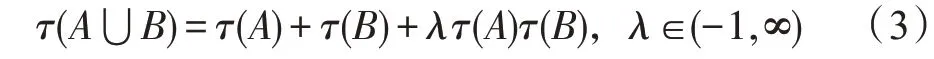
称()和()分别为关于集合和集合的云模型模糊测度。然后有：

（1）如果(⋃)=()+()，即=0，说明与相互独立；

（2）如果(⋃)＞()+()，即＞0，说明与信息互补；

（3）如果(⋃)＜()+()，即＜0，说明与信息冗余。

设为完全未知的云模型模糊测度，其定义为：

2.2 云模型双重积分算子

根据上述云模型与双重积分的定义，给出云模型双重积分算子，并进行讨论。

采用数学归纳法证明：

当=1 时，根据定义8 即可得证。

当=2 时，根据云模型的运算法则，可以得到：

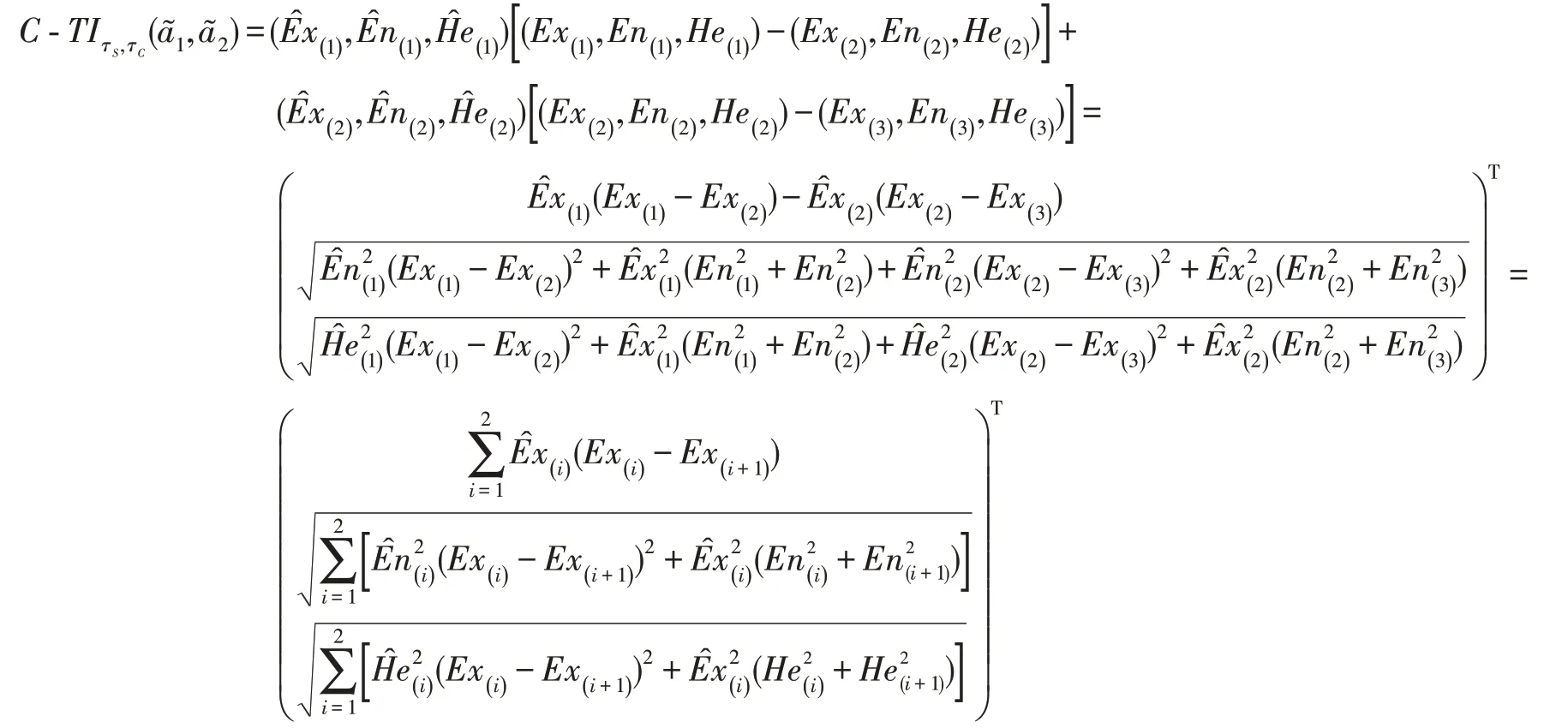
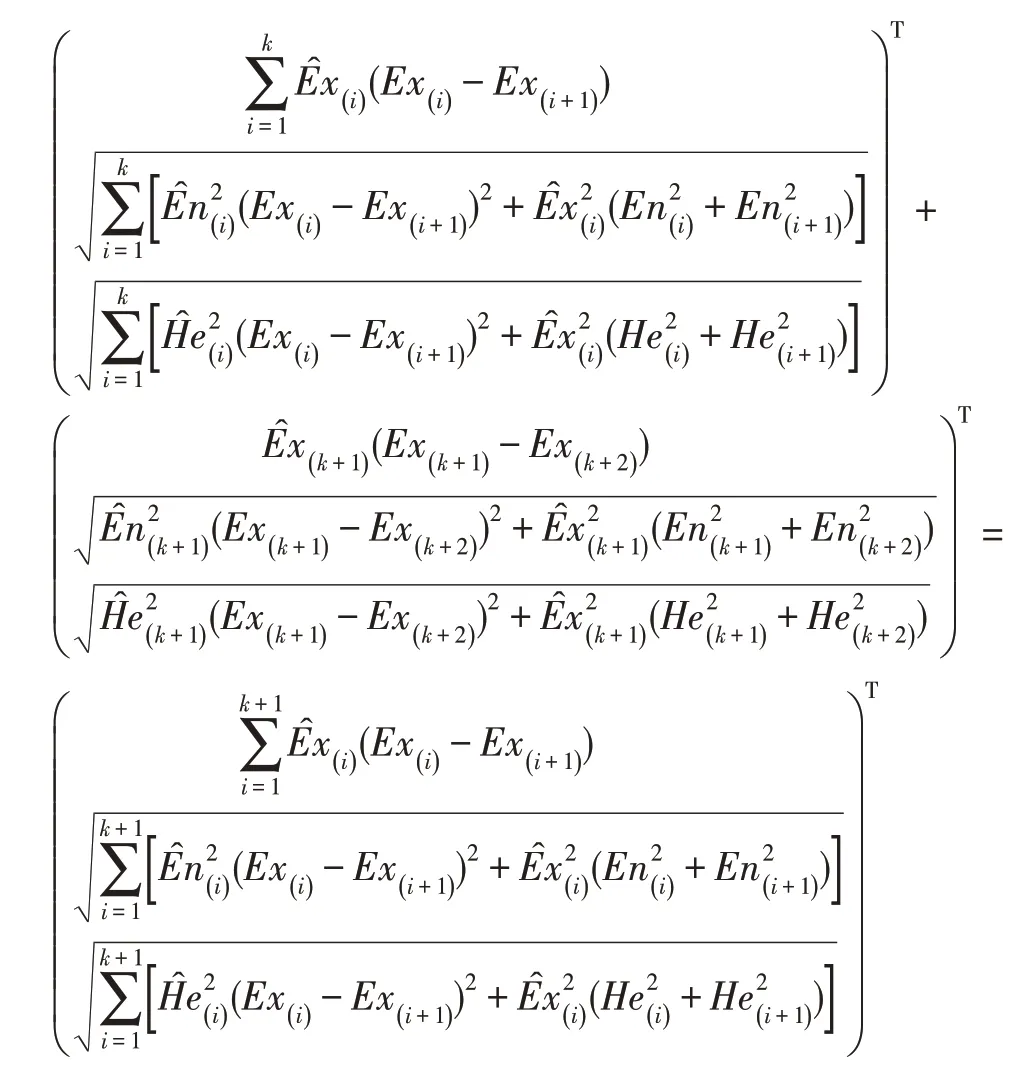
根据数学归纳法得出式（7）成立，因此定理1 得以证明。

由云模型的运算法则和定理1 可以得到云模型双重积分算子的如下性质：

3 云模型双重积分算子的层次多属性决策方法

由于事物普遍具有随机性和模糊性，可通过云模型将不确定的因素加以量化。此外，为了对决策对象进行整体评价，并考虑到指标之间的交互性问题，将双重积分作为各指标的聚合算子，通过权重的合理分配，基于云模型双重积分算子的层次多属性决策方法能够最大化反映评价中的不确定性，更加贴近现实生活，确保评价结果的真实可靠。

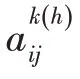
构建云模型决策矩阵。将属性值进行云变换：

式 中，=1,2,…,，=1,2,…,，=1,2,…,l，=1,2,…,。

本文通过个决策者各指标决策值的平均数来表示期望，可以直观地看出各方案指标值的高低水平，平均离差和方差分别表示熵和超熵，其中熵和超熵都能体现整体决策数据的离散程度，即反映出专家评分的随机性和波动性。平均离差是用指标值与平均值之间的绝对距离来表示数据的离散程度，方差表示整体数据的偏离程度，因此在决策值期望相同的条件下，平均离差小的指标评价值更高。当指标决策值的期望和平均离差相同时，方差小的决策值更高。运用期望、平均离差和方差三个统计变量作为云模型的三个数字特征能够充分反映决策值的波动程度，用来体现决策者在决策时的不确定性，通过式（17），将所有属性的决策值转换为云模型，可得到云模型决策矩阵：

确定指标和指标集的云模型模糊测度。本文用指标权重代替模糊测度，模糊测度的云变换与步骤1 指标值的云变换规则相同，分别将个决策者在每个指标下给定的权重值的平均数、平均离差和方差作为各属性模糊测度的三个数字特征，最终得到云模型模糊测度矩阵：

利用云模型双重积分算子对各方案主指标下的子指标进行集结。利用式（6）集结第个方案第个主指标下的个子指标决策值，集结结果为第个方案第个主指标的决策值。式（6）中涉及到的排序问题，将用定义2 给出的云模型比较规则进行比较，进一步得出各方案主指标的云模型决策矩阵：

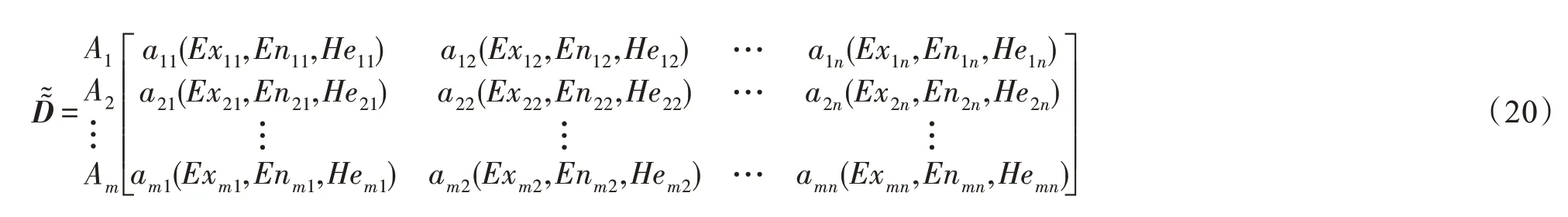
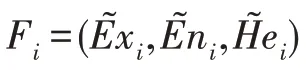
比较各方案综合决策值大小，选出最优方案。根据云模型比较规则对各方案的综合决策值F(=1,2,…,)进行排序，并选出最优方案。

4 案例分析

为了验证本文方法的有效性和实用性，将基于云模型双重积分算子的层次多属性决策方法应用到企业社会责任的评价中，具体评价步骤如下。

4.1 企业社会责任指标体系构建

企业若想获得可持续发展的能力，不能只注重产值、利润，还要追求人与自然的和谐、平衡，并且应为社会的发展做出贡献。企业社会责任逐渐成为企业竞争力的重要组成部分，企业社会责任作为一种新的企业价值，要求为消费者、员工、社区和环境等利益相关者承担责任，为可持续发展做出贡献。当企业拥有高的社会责任时，客户的忠诚度和满意度会增加，这也会影响消费者对企业品牌的信任，并增加消费者购买企业产品及服务的意愿。对企业社会责任进行评价会影响消费者的购买行为，同时树立更加友好的品牌形象，提升品牌竞争力。纵观现有研究，齐丽云等以G3 标准和ISO26000《社会责任指南》为基础，从责任治理等8 个社会期望主体的角度，构建了28 个指标的评价体系对企业社会责任绩效进行评价模型研究；Yen 等以经济、法律、伦理和慈善责任作为研究维度，基于16 项企业社会责任标准评价消费者的企业社会责任认知；Dimitriou通过分析不同的企业社会责任策略和计划，以利益相关者为导向，从员工、当地社区、顾客和环境四方面，将15 个欧洲机场作为样本，提供了机场社会责任的评估框架。综合以上分析，为了验证本文提出的基于云模型双重积分算子层次多属性决策方法的有效性，在专家咨询、综合阅读及整理文献的基础上，从人权、公共责任、公益实践、道德行为、环境和资源以及慈善行为的角度构建企业社会责任指标体系，见表1。

表1 企业社会责任指标体系Table 1 Index system of corporate social responsibility

4.2 评价步骤

为了全面评估云南省本地同行业中4 个企业的社会责任，邀请1 名具有资深阅历的高管及2 名企业管理专家分别对这4 个企业的社会责任利用本文所构建的指标体系及评价方法进行评价。首先，专家组对企业社会责任指标体系中的子指标进行打分，分值在0 到1 之间，初始评价结果见表2。

同理，专家组对各企业社会责任评价体系中子指标的权重进行评估，评估结果如表3 所示。

构建云模型决策矩阵。在对企业的社会责任打分时，专家的主观因素会影响评价结果的准确性，同时企业社会责任的指标体系具有亦此亦彼的特点，指标之间相互联系导致指标在评价时发生冲突，云模型的三个数字特征可以综合表示专家的评价信息。将表2 中的原始评价数据转化为云模型，转化结果见表4。

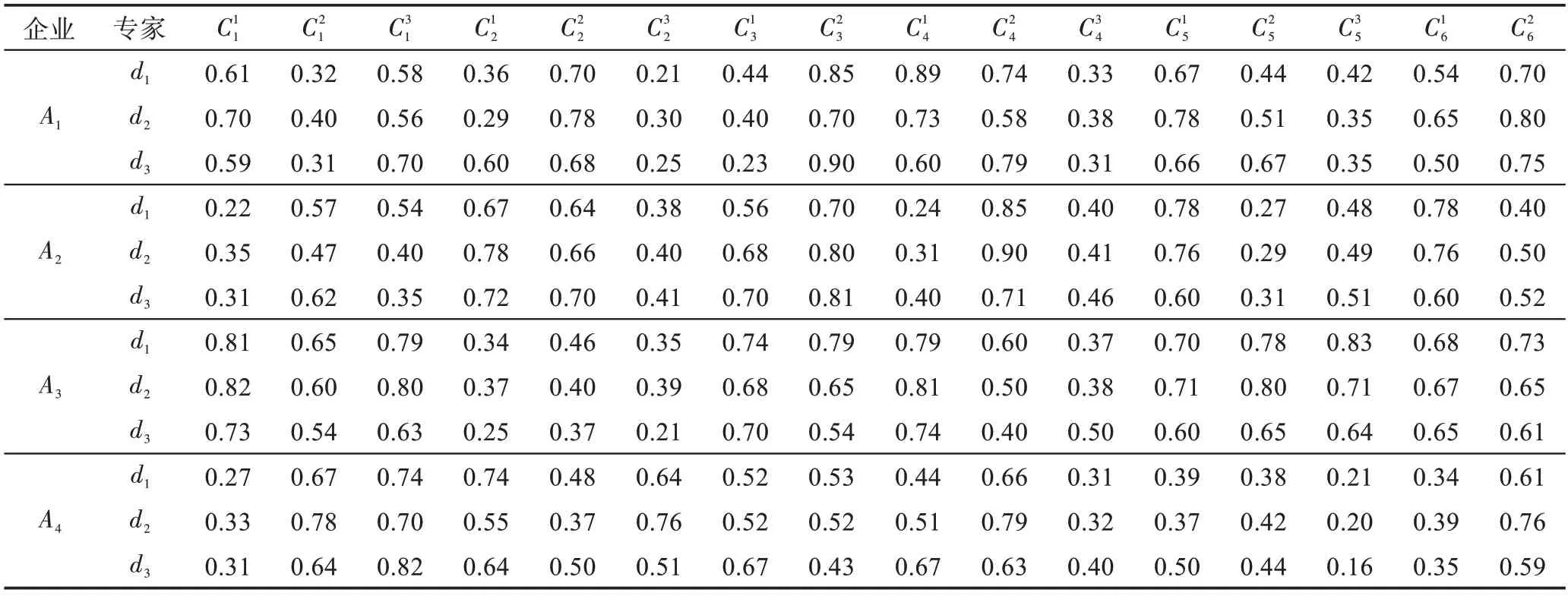
表2 子指标的初始评价结果Table 2 Initial evaluation results of sub-index

表3 子指标的初始权重Table 3 Initial weight of sub-index

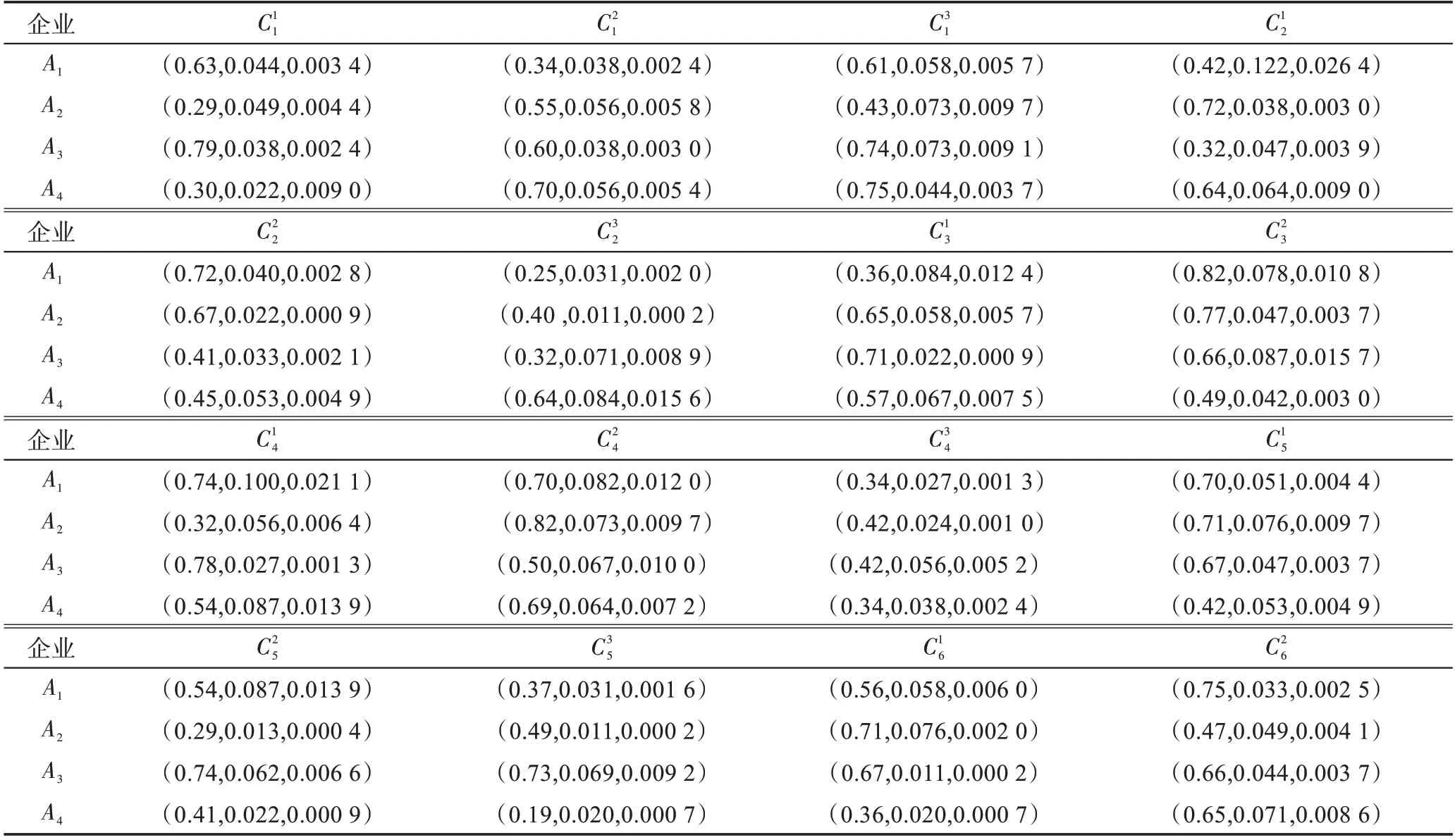
表4 子指标的云模型评价结果Table 4 Cloud model evaluation results of sub-index

确定指标集模糊测度。由于模糊测度与指标权重的含义相同，都是代表各指标的重要性程度，本文将指标权重视为模糊测度。同理将表3 中子指标的初始权重转换为云模型，见表5。

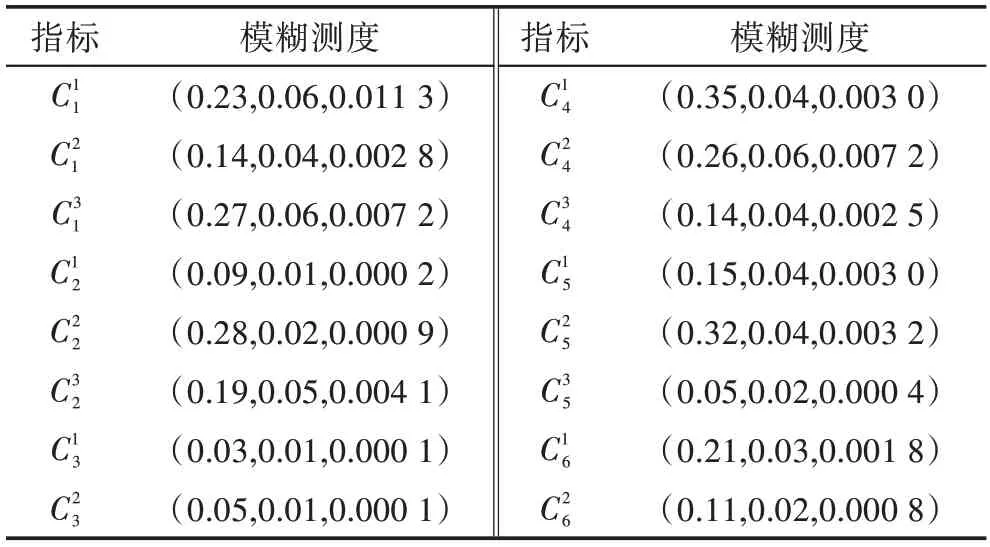
表5 子指标云模型模糊测度Table 5 Cloud model fuzzy measure of sub-index

集结各企业社会责任主指标对应下的子指标的权重（模糊测度），从而得到主指标的权重（模糊测度），各主指标的云模型模糊测度见表6。

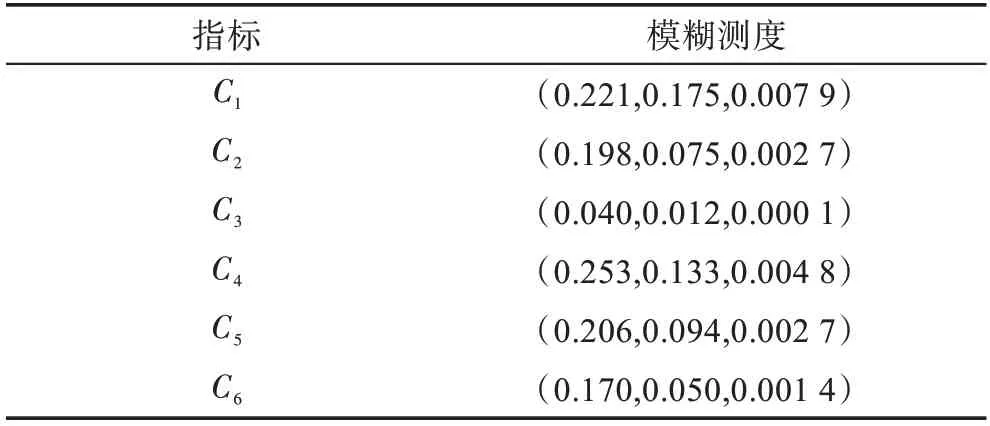
表6 主指标云模型模糊测度Table 6 Cloud model fuzzy measure of main indicator

已知主指标和子指标的云模型模糊测度，可计算各指标集的云模型模糊测度。由于篇幅有限，这里以企业的主指标为例，给出主指标下子指标集的云模型模糊测度。如表7 所示，将指标值由大到小排序，然后计算出参数的值为2.42，最后得出指标集的云模型模糊测度。用同样的方法可得到其他指标层的云模型模糊测度。

表7 指标值排序及其相应指标集的云模型模糊测度Table 7 Index value sorting and cloud model fuzzy measures of index set

确定各企业社会责任主指标的评价值。步骤2 已经得出了各企业社会责任指标集的云模型模糊测度，再利用云模型双重积分算子集结各企业社会责任主指标下子指标的评价值，其结果为主指标的评价值，最终结果见表8。

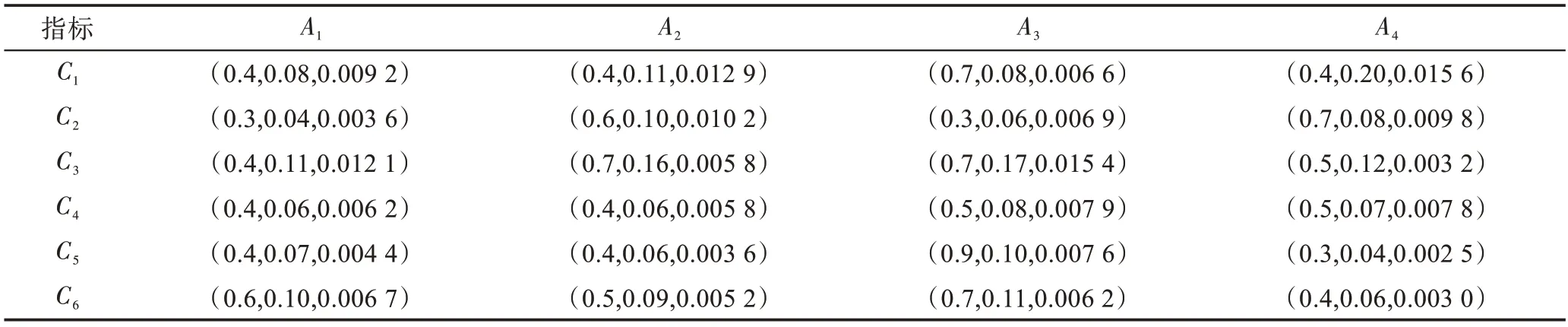
表8 主指标云模型评价值Table 8 Cloud model evaluation results of main indicator

确定各企业社会责任的综合评价值。按照计算主指标评价值相同的方法可计算各企业社会责任的综合评价值，得出=(0.39,0.24,0.013 2)，=(0.46,0.33,0.139 0)，=(0.55,0.35,0.014 6)，=(0.38,0.27,0.012 3)。

根据云模型比较规则，对各企业社会责任的综合评价值排序得＞＞＞，即企业的社会责任履行状况最优。

4.3 结果分析

通过以上评价步骤得出的企业社会责任在整体上得分最高。通过观察各企业社会责任指标的原始云模型评价值可以发现，企业大部分指标的得分值都位于前列，但是企业在环境与资源指标下得分较低。这不符合我国建设资源节约型和环境友好型社会的要求，因此企业需加大对环境和资源方面的关注力度，主要注意资源的合理利用、环境的有效管理以及品牌可持续发展能力的提升。企业的合规运营指标评分最高，可说明在企业的运营管理方面表现突出，但大多数指标得分仍处于较低水平，虽然在4 个企业中总得分处于第二的位置，但是仍需在其他方面做出合理改善。企业与企业的社会责任的各项指标都处于中下水平，从综合评价的结果来看，两个企业的评分总体差别不大，但企业的社区建设指标在全部评分中得到最低分，且社区建设指标权重较高，因此企业应高度重视当地社区的经济建设。综合以上分析，仍能得出的企业社会责任履行状况为最优，更加体现出基于本文方法进行企业社会责任评价的结果的准确性。

4.4 对比分析

为了进一步验证本文方法的有效性及优越性，把原始评价数据转化为精确数，并且将加权算数平均作为聚合运算符分别对本文中的算例进行对比分析。

（1）取3 个专家原始评价值的平均数作为子指标的最终评价值，再将权重用平均法转化为精确数值，然后用双重积分进行指标间的集成。此操作去除了企业社会责任指标评价信息的模糊性和随机性，得到最终评价值为=0.37，=0.44，=0.55，=0.42，排序得＞＞＞，企业社会责任仍为最优，但企业、企业排序发生了变化，这是因为精确的评价值忽略了专家在评价时的不确定性。例如，3 个专家给出的分数分别为（0.3,0.4,0.5）和（0.1,0.3,0.8），经计算得到两组数据的平均数都为0.4，但明显可以看出第二组数据的波动性更大、随机性更强，因此得出结论：精确数会忽略评价过程中的模糊性和随机性。通过以上分析，本文方法对处理企业社会责任评价时出现的随机性与模糊性有一定的有效性。

（2）通过加权算数平均法集结各企业社会责任指标的云模型评价值，计算结果得=(0.36,0.100,0.005 1)，=(0.30,0.079,0.003 7)，=(0.37,0.111,0.005 3)，=(0.31,0.093,0.004 5)，最终排序为＞＞＞。除了企业社会责任依旧最优之外，其余企业的排序与本文给出的评价方法所得的排序结果有所不同，由最终的综合评价值可以看出，4 个企业得分差距较小，相比本文方法其不能清晰地反映出各企业社会责任的履行状况水平，主要原因是通过加权算数平均法聚合指标的前提假设是指标相互独立，但实际的企业社会责任评价问题涉及到指标之间的相关性，以及指标评价值与指标权重的联系。因此，本文提出的评价方法能够考虑指标间的关联及整体的评价效果，继而更加贴近实际生活，评价结果也更加准确。

5 结论与展望

云模型可以应用于实际生活中的不确定问题，其能够更好地刻画事物的模糊性与随机性，本文首先利用云模型代替决策信息及模糊测度，并结合云模型理论与双重积分提出了云模型双重积分算子，并且证明了该算子的相关性质。云模型双重积分算子能够对复杂环境下具有关联性的指标值进行有效集结，并能够考虑到决策值与权重之间的侧重关系，相比现有的聚合算子其具备明显的优越性。其次基于云模型双重积分算子构建了层次多属性决策方法，用于系统的决策多属性问题。最后对云南省本地同行业中四家企业的社会责任进行评价。通过对比分析，进一步验证了本文所构建的聚合算子及决策模型的有效性和实用性。本文的不足之处是在构造云模型双重积分算子时，发现决策过程中的影响因素不唯一，因此最能够体现出决策水平的期望可能存在多个值，在以后的研究中可将二维云模型或者多维云模型与双重积分结合构建出新的算子，并应用于更多的决策领域中。