基于SCD-CNN 的域泛化自适应轴承故障诊断

2022-08-15徐伟烝

天津职业技术师范大学学报 2022年2期

李辉，徐伟烝

（天津职业技术师范大学机械工程学院，天津 300222）

基于传统信号处理方法的故障诊断技术，过度依赖于人工对故障特征的提取，会为故障诊断增加一定的不确定性，当机器运转工况复杂、振动信号中含有高强度噪声时，人工提取特定的故障特征更加困难[1-2]。随着人工智能技术的发展，机器学习、深度学习和智能模式识别等新方法已逐步应用于机械设备故障诊断。基于数据驱动的故障诊断方法，能把特征学习与故障分类融为一体，基于神经网络的智能特征提取代替了人工特征提取[3]。在故障诊断领域，Zhang 等[4]提出了一种基于宽卷积核的一维卷积神经网络（WDCNN）的轴承故障诊断方法，直接利用传感器采集的一维信号作为神经网络的输入，在卷积层使用小尺寸卷积核，利用数据增强技术产生更多的输入样本，实现了轴承故障的分类。李恒等[5]提出了一种基于STFT 和CNN 的轴承故障诊断方法，通过STFT 获得振动信号的2D 时频谱图，再将时频谱图作为2D 卷积神经网络的输入，实现故障分类。陈仁祥等[6]提出了一种基于CNN-DWT的轴承故障诊断方法，利用离散小波变换构造合适的时频矩阵，进而利用搭建的CNN 进行特征提取，采用softmax 分类器，利用BP 算法调整结构参数，实现故障分类。袁建虎等[7]采用Morlet 小波变换构造振动信号时频图，建立CNN 分类模型，实现了滚动轴承故障的智能诊断，但该方法对时频图进行压缩时会丢失部分特征，导致一定程度的故障类型误分。Shao 等[8]对振动信号进行CWT，并基于VGG-16 预训练模型进行参数迁移，实现了齿轮箱的故障诊断。胡晓依等[9]将SVM 引入卷积神经网络，提出了一种基于CNN-SVM 的轴承故障诊断方法，直接对原始实测信号进行学习和分类，对不同损伤程度的轴承实现了99%的识别准确率。鄢仁武等[10]利用连续小波变换和二维卷积神经网络，实现了高压断路器操纵机构的故障识别。Islam 等[11]采用小波包变换得到一维信号的二维构造矩阵，将其作为CNN 的输入，自动进行故障识别。深度学习在机械设备故障诊断领域的研究成果，很大程度上实现了机械设备故障诊断的自动化，但常见的深度学习方法往往假设训练数据和测试数据来源于同一工况，不仅难以适用于不同工况的检测数据，而且为实时跨域故障诊断的应用带来了障碍。

域泛化（domain generalization，DG）是深度学习领域非常热门的一个研究课题，主要研究从若干个具有不同数据分布的数据集（领域）中学习一个泛化能力强的模型，以便在未知（unseen）的测试集上取得较好的效果[12-14]。轴承故障振动信号为典型的循环平稳信号[15-16]，谱相关密度（spectral correlation density，SCD）能有效提取轴承的故障特征[17-19]，更易于卷积神经网络对信号特征的学习和提取。本文针对变负载工况、少样本数据和样本数据类别不平衡（class imbalance）3种工业场景，提出基于谱相关密度和卷积神经网络的轴承故障诊断技术。

1 CNN 常用信号预处理方法

卷积神经网络常使用二维图像作为输入层，因此在基于卷积神经网络的故障诊断技术中，常将一维振动信号采用信号预处理方法转化为二维图像。常用的信号预处理方法有：短时傅里叶变换（short-time Fourier transform，STFT）和连续小波变换（continuous wavelet transform，CWT）等，本文采用谱相关密度作为信号预处理方法。

1.1 短时傅里叶变换

连续信号x（t）的短时傅里叶变换可表示为

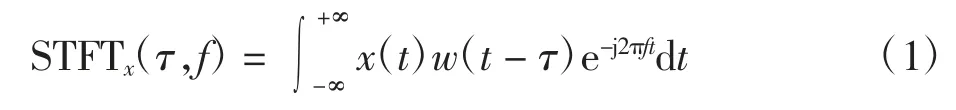
式中：w（t - τ）为中心在t 的有限长度窗函数；t 为时间；f 为频率。

STFT 将信号x（t）映射到时频（τ，f）平面内。

1.2 连续小波变换

小波变换是连续信号x（t）的时间-尺度表示，信号x（t）的连续小波变换可表示为

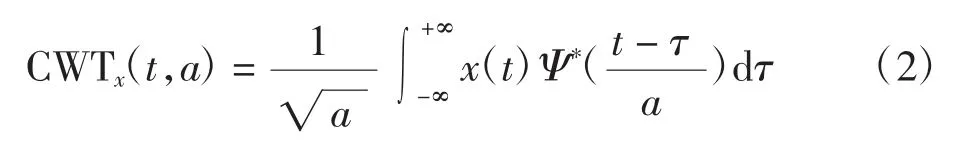
式中：a 为小波尺度因子；τ 为小波频移因子；Ψ（·）为小波母小波；*为复共轭。

CWT 将信号x（t）映射到时间-尺度（t，a）平面内。

1.3 谱相关密度

对于循环平稳实信号x（t），其时变自相关函数为

式中：τ 为时间滞后量；E[·]为数学期望。

时变自相关函数Rx（t，τ）可展开为傅里叶级数形式，即

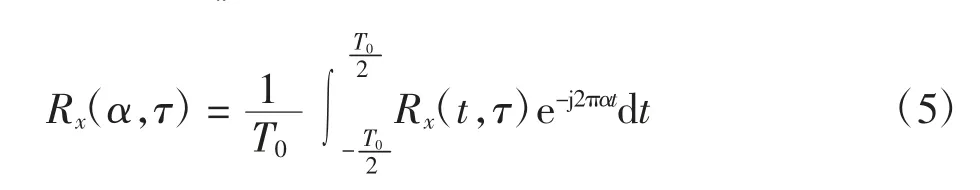
谱相关密度定义为Rx（α，τ）的傅里叶变换，即

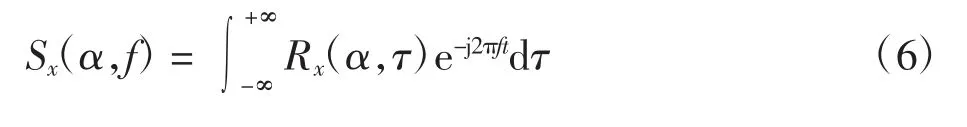
2 轴承故障特征提取性能对比

为充分说明SCD-CNN 方法的优良性能，首先利用美国凯斯西储大学（CWRU）电机滚动轴承数据[20]，比较说明STFT、CWT 和SCD 的轴承故障特征提取能力。诊断对象为SKF6205 深沟球轴承，电机振动信号采样频率为48 kHz，电机转速1 772 r/min，负载1 hp，每个数据的采样点数为1 024。轴承滚动体故障数据序号为123，内圈故障数据序号为110，外圈故障数据序号为116，轴承正常状态数据序号为98。轴承振动信号如图1 所示，图1（a）至图1（d）分别为轴承滚动体故障（BF7）、内圈故障（IF7）、外圈故障（OF7）和正常状态（NC）的振动信号。

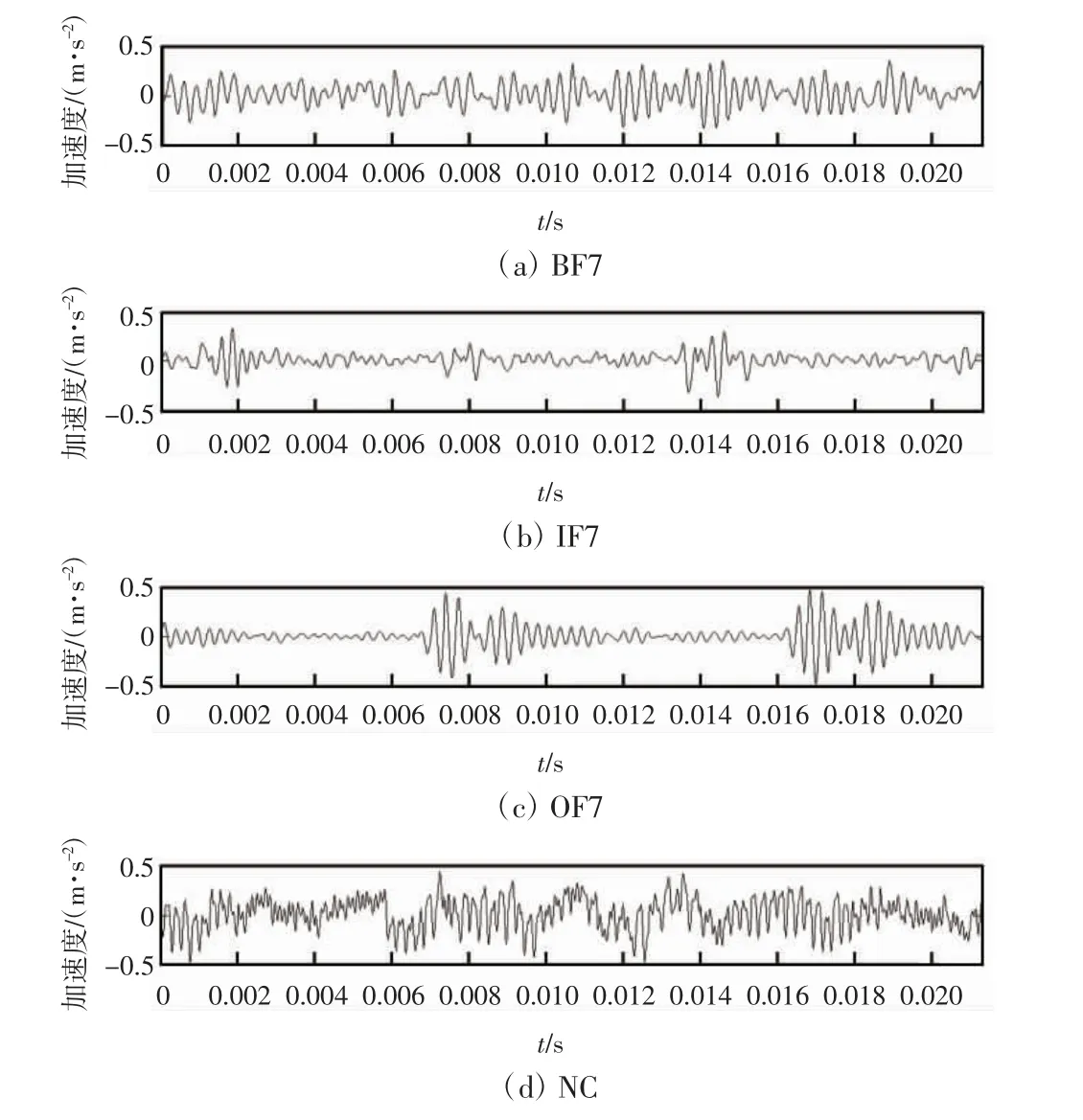
图1 轴承振动信号

图2 为图1 所示轴承振动信号的短时傅里叶变换（STFT），采用汉明窗函数，时间窗宽度为128 个采样点，重叠点数为64 个采样点。

从图2（a）至图2（c）可以看出，当轴承出现故障时，轴承振动信号的能量主要集中在较低频率范围（0～4 kHz）。从图2（d）可以看出，当轴承正常时，轴承振动信号的能量集中在较宽的频率范围内（0～8 kHz），能量比较分散。从图2 可以看出，短时傅里叶变换的频率分辨率较高，而时间分辨率较低。尽管当轴承出现不同类型的故障时，其短时傅里叶变换的时频图具有不同的形态，但从短时傅里叶变换时频图中，难以发现不同故障类型的故障特征。主要原因是由于STFT 采用的窗函数为固定时间窗，很难同时兼顾时间分辨率和频率分辨率。此外，STFT 只对频率波动较小的平稳信号具有较好的时频分析效果，对频率波动大的非平稳信号进行分析时，会出现性能衰退甚至失效。

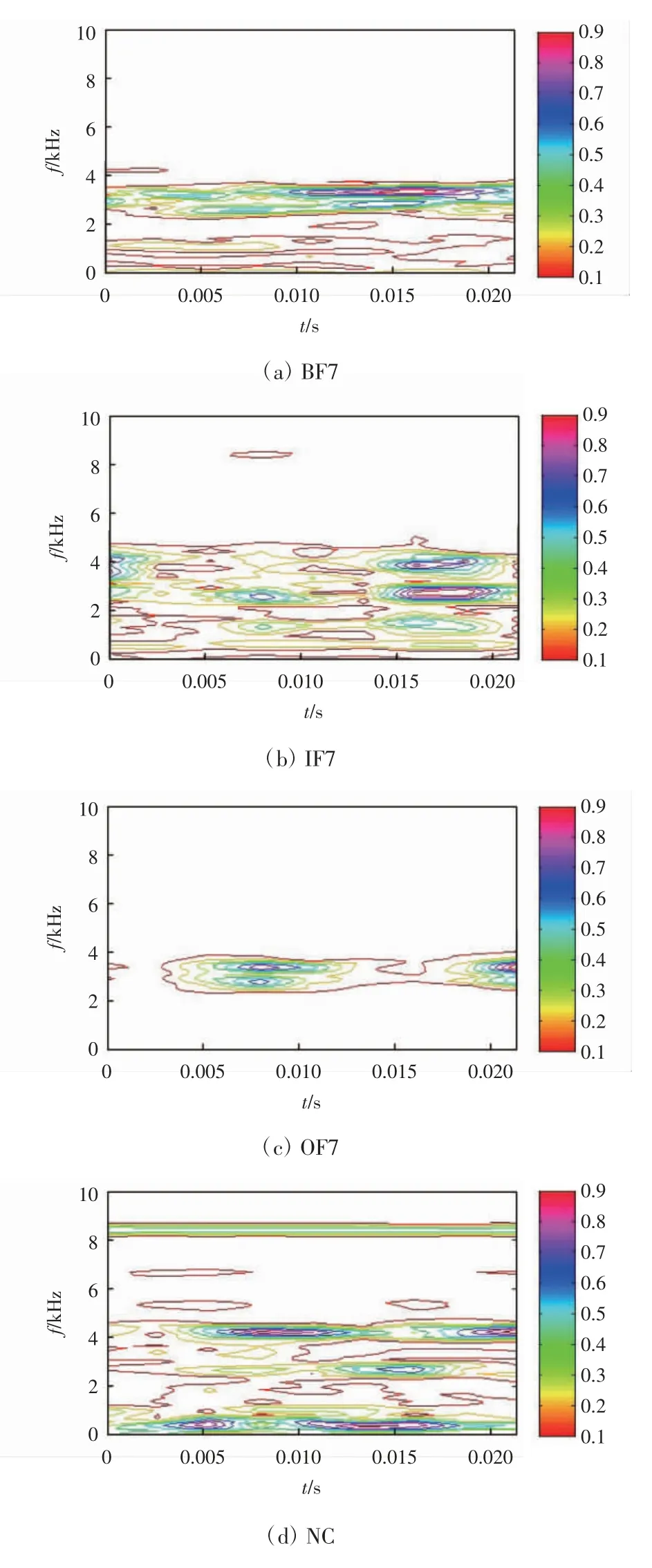
图2 轴承振动信号的STFT

图3 为图1 所示轴承振动信号的连续小波变换（CWT）时间-尺度图，采用Morlet 小波。

从图3（a）至图3（c）可以看出，当轴承出现故障时，轴承振动信号的能量也主要是集中在较低的小波尺度范围（10～20）。从图3（d）可以看出，当轴承正常时，轴承振动信号的能量集中在较宽广的小波尺度范围内（10～80），能量也比较分散，与STFT 分析结果基本一致。

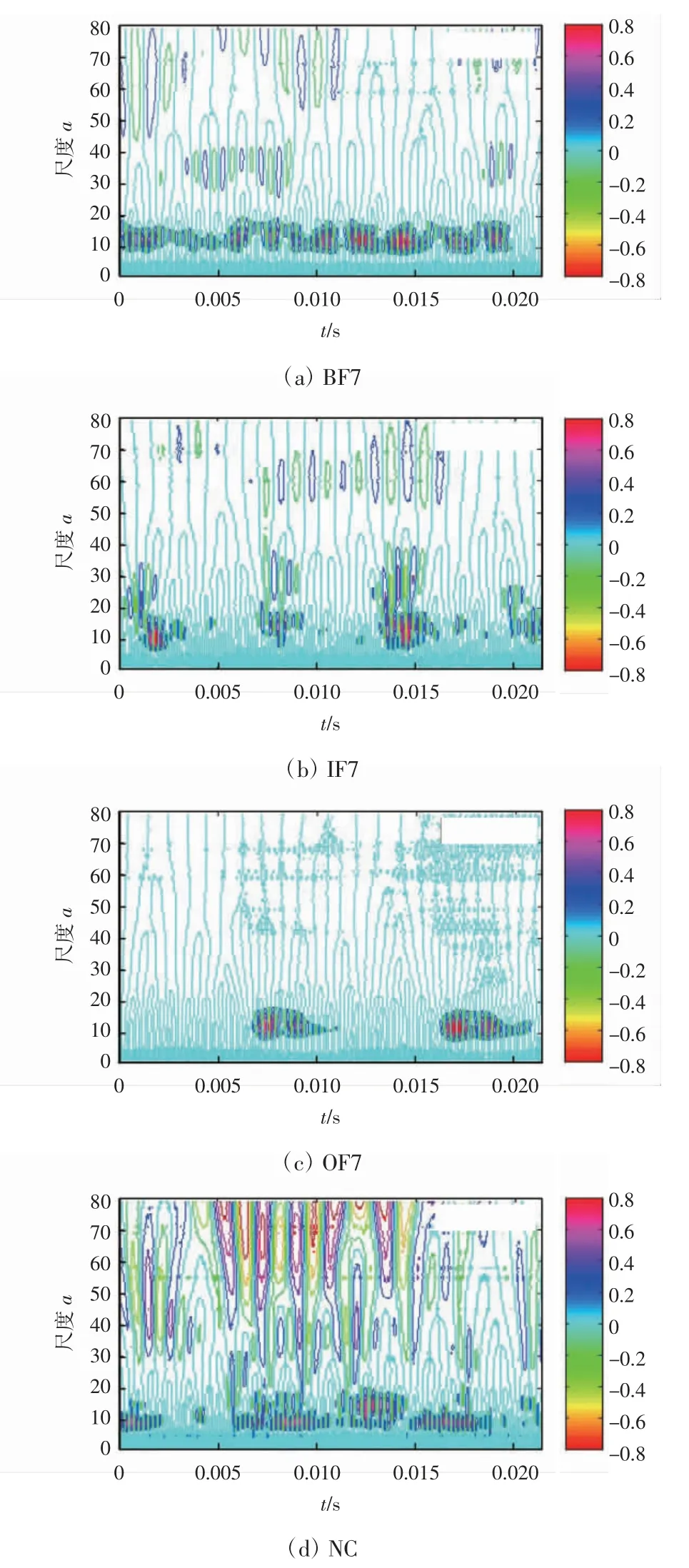
图3 轴承振动信号的CWT

对比图2 和图3 可以发现，小波变换的时间分辨率较高，而频率分辨率较低，小波变换能比较准确地提取轴承故障信号中的瞬时冲击特征，其性能优于短时傅里叶变换。虽然CWT 能有效提取振动信号的瞬时冲击特征，但从图3（a）至图3（c）中也很难发现反映轴承故障类型的时间-尺度特征，这主要是由于小波基函数的选取会影响故障分析的效果。因此，STFT 和CWT 在处理循环平稳信号时都存在一定的局限性，尤其当振动信号含有较强的噪声干扰时，STFT 和CWT更难取得较好的分析效果。

图1 所示轴承振动信号的谱相关密度（SCD）图如图4 所示。

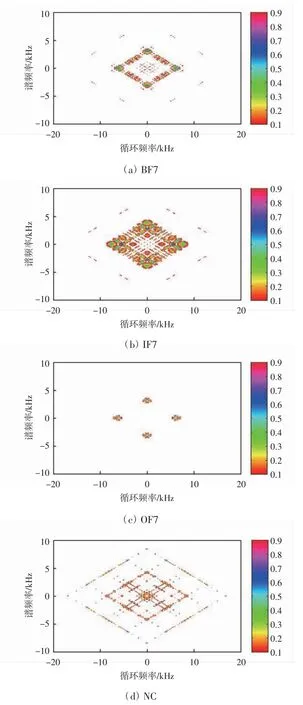
图4 轴承振动信号的SCD

谱相关密度图整体呈菱形结构，体现了SCD 特有的谱相关特性。在构成的双频平面内，SCD 关于α 轴和f 轴对称，并且呈菱形分布，对于呈大菱形分布的每个谱峰簇而言，其内部都存在4 个小菱形，且任意一小菱形水平方向对角线长度为轴承故障特征频率的2倍，在竖直方向对角线长度等于轴承故障特征频率。由于轴承故障类型不同，其故障特征频率也不同。因此，从图4 可以看出，不同的轴承故障类型，其谱相关密度图也不同，谱相关密度能很好地刻画轴承的故障特征，根据谱相关密度图能有效区分轴承的故障类型。

对比图2、图3 和图4 可知，SCD 比STFT、CWT 可以更好地刻画轴承的故障特征，因而能为CNN 提供更高质量的输入数据，提高CNN 特征学习和故障特征识别能力。

3 SCD-CNN 故障诊断方法

3.1 卷积神经网络结构参数

CNN 结构主要由输入层、卷积层、池化层、全连接层和输出层组成。本文的CNN 主要包含2 个卷积层，2个批归一化层，2 个池化层，2 个全连接层和1 个Softmax 输出层，所有激活函数均采用ReLU 函数。CNN 主要结构参数如表1 所示。

表1 卷积神经网络结构参数

3.2 SCD-CNN轴承故障诊断流程

SCD-CNN 故障诊断方法包括对轴承故障振动信号进行重叠采样，构建训练集和测试集，数据预处理计算样本谱相关密度，训练CNN 模型，CNN 特征提取与识别等。SCD-CNN 轴承故障诊断流程图如图5 所示。

图5 SCD-CNN 轴承故障诊断流程图

4 SCD-CNN 故障诊断方法泛化性能

机械设备运行工况复杂，研究卷积神经网络在变工况、少样本和类别不平衡情况下，能否有效提取故障特征以及对不同数据分布的自适应能力，具有重要的学术价值和工程实际意义。CWRU 电机轴承振动信号数据集，包括不同损伤位置、不同损伤程度、不同负载、不同转速等工况，依据轴承损伤位置分为轴承滚动体损伤、内圈损伤和外圈损伤，不同的损伤位置还分别对应3 种不同的损伤直径：0.007 inch、0.014 inch 和0.021 inch。将轴承滚动体、内圈、外圈损伤和正常状态分别标记为BF7、BF14、BF21、IF7、IF14、IF21、OF7、OF14、OF21 和NC 共10 个类别。根据电动机负载和转速不同，将数据分为数据集A（负载1 hp、转速为1 772 r/min）、数据集B（负载2 hp、转速为1 750 r/min）和数据集C（负载3 hp、转速为1 730 r/min）。本节应用CWRU 轴承数据集，在变负载工况、少样本数据和样本数据类别不平衡3 种实际工业场景下，研究SCDCNN 模型的泛化能力。

4.1 变负载工况下SCD-CNN泛化性能

机械设备经常工作在变负载工况下，在某种负载工况下训练的故障诊断模型，期望将其迁移到其他负载工况也具有良好的自适应性能，能得到比较高的故障识别准确率。由于机械设备的工作负载不同，传感器采集信号的幅值、振动周期、特征个数以及相位等均存在较大差异，可能会对诊断模型产生严重干扰。在变负载工况下，检测SCD-CNN 模型的自适应性能，源域数据用于训练CNN，目标域数据用于测试CNN 的域泛化自适应性能，在源域负载条件下训练的故障诊断模型，将其迁移至负载变化的目标域进行自适应性能测试，变负载工况下自适应数据集如表2 所示。

表2 变负载工况下自适应数据集

在表2 中，训练集每类故障样本数为600 个，测试集每类故障样本数为200 个，每个样本的采样点数为2 048，根据表1 的CNN 参数和SCD-CNN 轴承故障诊断流程图进行测试，并与STFT-CNN 和CWT-CNN 模型实验结果进行对比分析，结果如图6 所示。

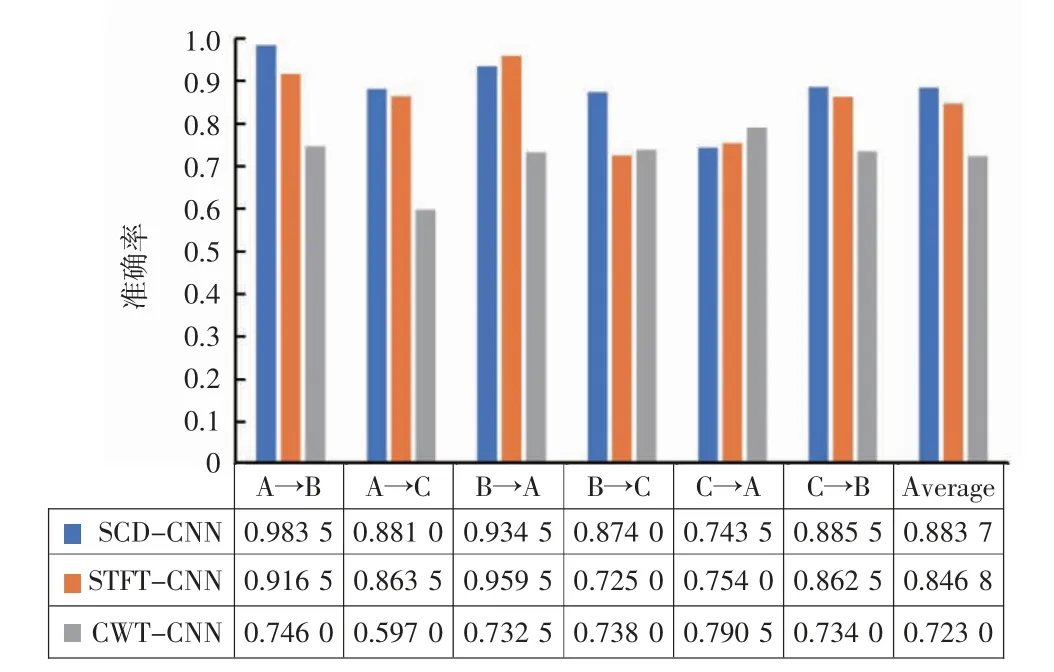
图6 变负载工况下故障识别准确率对比

从图6 可以看出，SCD-CNN 故障诊断模型，在变负载工况下的平均识别准确率接近90%，高于STFTCNN 和CWT-CNN 故障诊断方法，其中CWT-CNN 方法在变负载工况下的泛化力最差，平均故障识别准确率低于75%。此外，不难发现当负载变化相差1 hp 时，SCD-CNN 模型的泛化力较好，故障识别准确率变化较小，而当负载变化相差2 hp 时，使用训练集C（负载3hp）来训练模型，对测试集A（负载1 hp）进行诊断验证时，SCD-CNN 模型的识别正确率低于80%，说明当负载变化大时，振动信号的幅值、周期、特征个数或相位等存在较大的差异，对模型的稳定性有一定的影响。总体上，SCD-CNN 模型在负载变化较小工况下的自适应能力很强，在负载变化较大工况下的自适应力较差，但其泛化性能优于STFT-CNN 和CWT-CNN 模型，具有较好的变负载自适应力。

4.2 少样本条件下SCD-CNN泛化性能

在利用大数据训练模型的驱动下深度学习已在许多领域中取得了广泛应用。但在现实应用场景中，有时很难得到大量的数据，并且在监督学习方式下，对大量数据样本添加标签会耗费大量时间。因此，期望通过用少样本学习得到解决问题的稳定模型，减少对大量训练数据的依赖。

基于标准CWRU 轴承数据集，在少样本数据下对轴承故障诊断模型的泛化力进行研究，按照6 ∶2 ∶2 划分训练集、验证集和测试集，每类故障样本数分别为800、500、300和100个，对SCD-CNN、STFT-CNN和CWTCNN 模型分别进行实验，实验结果如图7 所示。

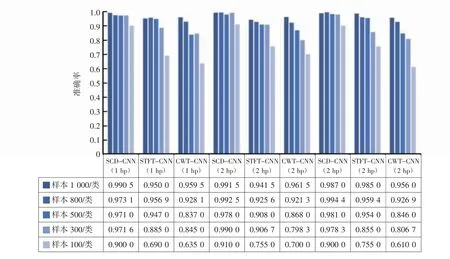
图7 少样本条件下故障识别准确率对比

由图7 可知，SCD-CNN、STFT-CNN 和CWT-CNN模型，在不同负载下的故障识别率，总体上随着数据集样本数的减少呈下降趋势。其中，当每类故障样本分别为1000、800、500 和300 个时，SCD-CNN 诊断模型的故障识别准确率接近，因此可适当减少训练样本的个数，节约神经网络计算时间，提高模式识别效率，同时对故障识别准确率影响较小。与STFT-CNN 和CWTCNN 相比，当每类故障样本分别为1000、800 和500个时，STFT-CNN 方法的故障识别准确率波动小于CWT-CNN，即STFT-CNN 模型的泛化力高于CWTCNN。当每类故障样本数为100 个时，SCD-CNN 方法的故障识别准确率远高于STFT-CNN 和CWT-CNN方法，其故障识别准确率与STFT-CNN 和CWT-CNN方法，在每类故障样本为300～500 个时的准确率相当。由此可见，基于SCD-CNN 滚动轴承故障识别方法，在少样本学习情况下，当不对模型进行微调时，仍具有较好的泛化性能。

4.3 类别不平衡条件下SCD-CNN泛化性能

在实际工作场景下，滚动轴承产生的故障类型和故障程度都是随机的，且轴承故障工况下样本数量较少，而正常工况下的样本数量较多，因而研究类别不平衡情况下卷积神经网络的泛化性能，也具有很现实的应用价值。类别不平衡是指在分类任务中，不同类别的训练样本数存在很大差别的不均衡情况。在本节中，使用负载为1hp 的CWRU 轴承数据集进行实验，将正常样本作为多数类，将全部故障样本作为少数类，且少数类中包含的9 种故障类型的样本数分别相等，每类故障样本与正常样本比为1 ∶10。

设定不平衡率为每类故障样本/正常样本，构建不平衡率为1 ∶2、1 ∶10、1 ∶100 和1 ∶200 四组实验，具体样本信息如表3 所示。以不平衡率1 ∶200 为例，将定工况为1 hp 的CWRU 轴承数据集进行划分，不平衡率1 ∶200 的数据集划分（负载1 hp）如表4 所示。

表3 类别不平衡样本信息

表4 不平衡率1 ∶200 的数据集划分（负载1 hp）

神经网络分类效果的评价指标主要包括准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1-score 等。使用以上4种评测指标，对SCD-CNN、STFT-CNN和CWT-CNN 模型进行实验，实验结果如表5 所示。

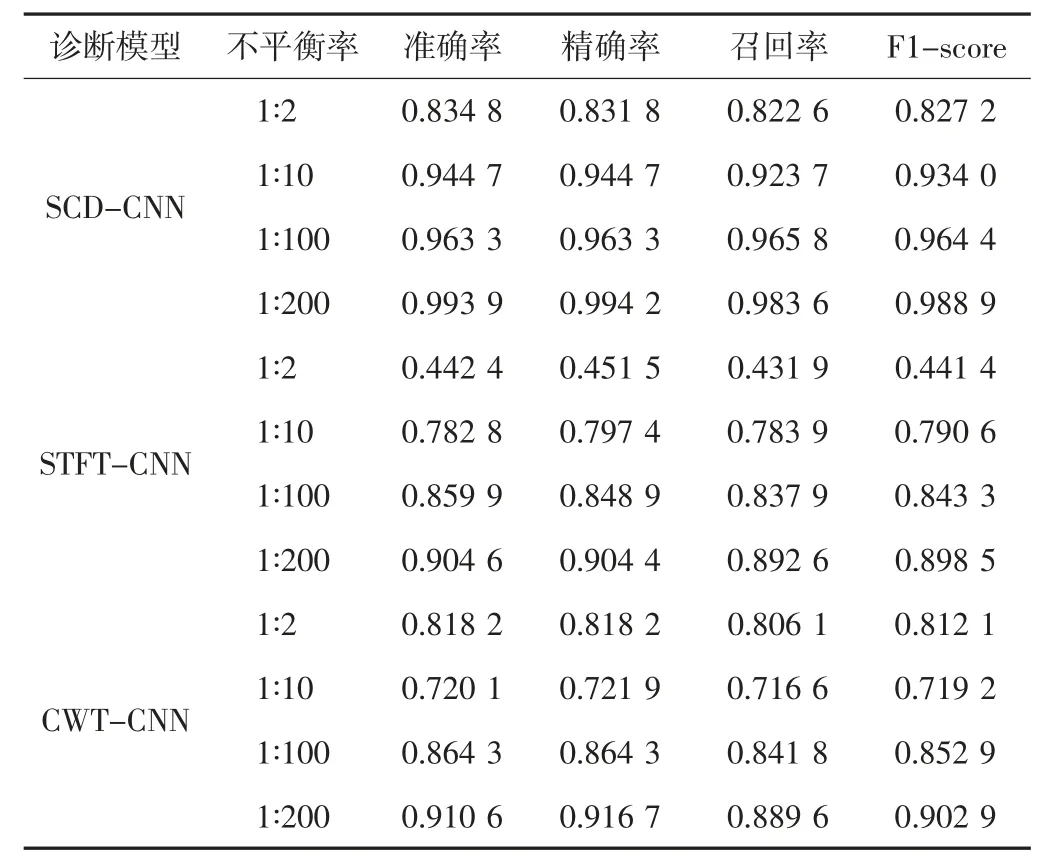
表5 不均衡数据集诊断结果

从表5 可以看出，随着不平衡率的提高，正常样本（多数类）的数据量也逐渐增加，分类的准确率不断提高。这是由于正常样本数占主导，故障诊断的准确率向正常样本倾斜，但这并不能准确反映模型对故障样本的检测能力。观察SCD-CNN、STFT-CNN 和CWT-CNN模型的召回率和F1-score 指标，SCD-CNN 模型的召回率和F1-score 指标在不同的不平衡率下，均高于STFT-CNN 和CWT-CNN 模型，说明SCD-CNN 模型对少数类故障检测能力上优于STFT-CNN 和CWTCNN 模型，在数据类别不均衡场景下的故障诊断能力较强。